
ГОС математика / Мат. ан / 7,8,9
.doc|
Вопрос 7. Исследование ф-и на экстремум. Задачи на наибольшее и наименьшее значения ф-и.
Опр:!
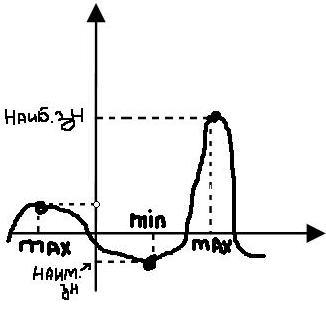
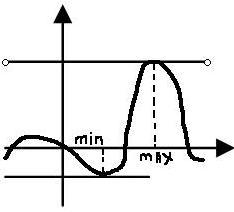
ф-ия опред-на на множ-е Х, х0 Геом.смысл:
max-под касат-ой, min-над касат-ой.
Опр:
х0 наз-ся
критической
точкой
ф-ии f(x),если
в этой точке произв-ая не Опр: критич-ая т.,в кот-ой произв-я =0,наз-ся стационарной т. Th Ферма:
!ф-ия опред-на на
некот-м промеж-ке Х, х0 Док-во:
По условию f
‘(x)
дифф-ма в т. х0
=>
!ф-ия f(x) в т. x0 принимает наиб-ее знач-ие (для наим-го док-во аналог-но).
1)Оценим
2)Рассм-им
Из 1) и 2) =>что
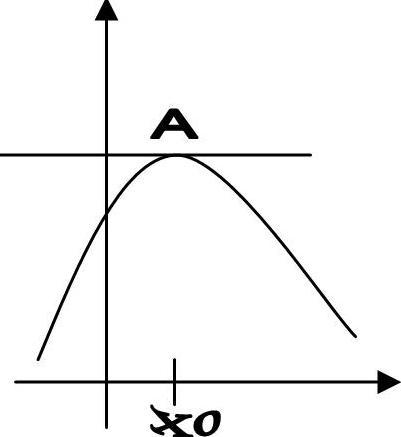
пределы совпадают и =0 => lim Геом.смысл: В некоторой точке на кривой имеющей абсциссу x0 касательная ||-на оси ОХ
Th (необх.усл. сущес-ия экстремума) ! ф-ия имеет произв-ю в т. экстремума. Тогда эта производная=0. Док-во:
Т.к по условию
ф-ия дифф-ма, у нее Th (1-ое достат.усл. сущес-ия экстремума) !ф-ия f(x) в окрест-ти (х0 - δ; х0 + δ) точки, за исключением, может быть т. х0 имеет конечную произв-ю f ‘(x), обладает св-ом постоянства знака на промеж-ке (х0 – δ) и (х0 + δ). Возможны случаи: 1) f ‘(x)<0 при x<х0, f ‘(x) >0 при x>x0. По доказанной выше Th f(x) возрастает на (х0; х0+ δ),f(x) убыв-ет на (х0+ δ; х0). Т.о значение f(х0) явл-ся наим-им в окрест-ти (х0 - δ; х0 + δ); х0-точка min. 2) f '(x)>0 при x< х0, f ‘(x)<0 при x> х0.Тогда f(x) возр-ет при x< х0, f(x) убыв-ет при x> х0. Т.о значение f(х0) явл-ся наиб-им в окрест-ти (х0 - δ; х0 + δ); х0-точка max.
3) f
‘(x)>0
при x<
х0,
f
‘(x)>0
при x>
х0.Тогда
f(x)
возр-ет при x<
х0,
f(x)
возр-ет при x>
х0.
В этом случае в Вывод: Если при переходе через т. х0 производная f ‘(x) меняет знак, то х0-точка экстр-ма. Если при переходе ч/з т. х0 произв-ая f ‘(x) меняет знак с “–“ на “+”, то х0-т.min. Если произв-ая меняет знак с “+“ на “-”, то х0-т.max.
Если произ-ая не
меняет знак, то экстр-ма в т. х0
не Th (2-ое достат.усл. сущес-ия экстремума) Пусть f ‘(x0)=0, f “(х0)≠ 0. Тогда, если f “(х0)>0, то т.х0- т.min, если f “(х0)<0, то х0- т.mах. Док-во: ! х0 явл-ся стац-ой точ.ф-ии f(x)(т.е. f ‘(x0) =0); f ‘‘(x0). Возможны 2 сл: 1) f ‘‘(x0) >0,
f
‘‘(x0)
=lim
f
‘(x0)
=0, значит f
‘‘(x0)
=
По св-ву предела
ф-ии в точке при значениях х близких
к x0
Т.о по 1дост.усл.
x0
-точка min.
Аналогично показ-ся при
Нахождение наиб и наим значения. !дана ф-ия f(x)-непрер.на [a;b],тогда по Th Вейерштрасса ф-ия достигает наиб и наим. значения. План нахож-ия: 1.найти критич-е точки. 2. найти знач-ие мФ-ии в крит-их точках и на концах отрезка 3.из всех выбрать наиб. или наим. [Th Вейерштрасса: если ф-ия непр-на на отрезке, то на этом отр-ке она достигает своих точных(верхних и нижних)границ] Задача. Бак, имеющий вид прямоуг. парал-да с квадр. основанием, должен вмещать V литров жидкости. При какой стороне основания площадь пов-ти бака (без крышки) будет наим.? 1 этап. Составл. матем. модели. Оптимизируемая величина-площадь пов-ти бака S,т.к. в задаче требуется выяснить, когда эта площадь будет наим. S зависит от измерений прямоуг. парал-да. Пусть независимая переменная х- сторона квадрата в основании бака, х>0. Если h-высота бака, то V=x2h, откуда находим h=V/x2. S=x2+4V/x2*х=x2+4V/x. 2 этап. Работа с составленной моделью.(f ‘(x), f ‘(x)=0, знаки производной, сравниваем) 3 этап. Ответ на вопрос задачи. ШКМ (эта Th есть, испол-ся для исслед-ия ф-ий и постр-ия графиков) Колмогоров: вводится понятие критических точек, необходимое условие экстремума называется теоремой Ферма. Приводится признак max (знак меняется с + на -) и min (знак меняется с - на +). Есть правило отыскания наиб. и наим. знач. Для решения задач предлагается следующая схема: 1. перевести задачу на язык функций (выбрать х) 2. найти наиб, или наим. знач. этой функции на некот промежутке 3. выяснить, какой практический смысл имеет полученный результат. Мордкович: опр. max и min ф-ии, стационарные, критич. точки. Теорема: Если функция имеет экстремум в точке, то в ней производная функции либо равна 0, либо не сущ-т Приводятся достаточные усл. экстремума (max, min, когда экстремума нет-если слева и справа от точки знаки производных одинаковы), алгоритм исследования функции на монотонность и экстремумы, наиб. и наим. знач. Теорема о том, что в точке min-наим. знач, а в точке max-наиб. Схема решения задачи: 1. Составление мат. модели 2. Работа с составленной моделью 3. Ответ на вопрос задачи. В шк уч-ке Мордковича материал более близок к курсу высшей мат-ки.
|
Вопрос 8. Первообразная и неопределенный интеграл. Опр. Ф-ия F(x) задан-я на мн-ве Х и диф-мая на Х наз. первообразной для ф-ии f(x) на этом мн-ве, если F'(x)=f(x). Пр. F(х)=х4/4-первооб-ая для ф-и f(x)=x3, т.к. F’(x)=(x4/4)=x3 У функции бесконечно много первообразных.
Теорема.
Пусть F(х)-
первооб-ая для ф-и f(х)
на [a,b],
тогда Обратно: всякая первооб-ая для f(x) в указанном промежутке может быть представлена в виде F(x)+С, где C=const. Т.е. все первооб-ые ф-ии f(х) отличаются друг от друга только постоянной. Если для данной ф-и f(x) известна одна первооб-я F(x), то мн-во всех ее первообр-х представляется выражением F(x)+C, где C=const.
Опр Совокупность всех первообразных для ф-ции f(x) на (а;в) наз. неопред интегралом от ф-ции f(x). Обозн. ∫f(х)dx. Т.е. ∫f(х)dx=F(x)+C. Произведение f(х)dx наз подинтегральным выражением, а ф-ия f(х) – подинтегральной ф-ей. Геом смысл. Если построена какая-нибудь интегральная кривая, то все остальные интегральные кривые получаются из нее парал-м переносом вдоль оси Оу. Восстановление ф-ции по её производной или нахождение неопр интегр по заданной подынтегр ф-ции наз. интегрированием. Св-ва неопределенного интеграла.
(F(x)+C)’=F’(x)=f(x) 2. Диф-ал от неопред инт-ла=подъинтегральному выражению: d ∫f(x)dx=f(x)dx #(∫f(x)dx)’dx=(F(x)+C)’dx=F’(x)dx= =f(x)dx# 3. Неопред. Интеграл от диф-ла некот ф-ии равен сумме этой ф-ии и произв постоянной ∫F(x)dx=F(x)+C #∫F’(x)dx=∫f(x)dx=F(x)+C# 4. (линейность) ∫kf(x)dx=k∫f(x)dx. # (∫kf(x)dx)'=kf(x) и (k∫f(x)dx)'=k(∫f(x)dx)'=kf(x) =>∫kf(x)dx=k∫f(x)dx# 5. (адьютивность) ∫(f(x)±g(x))dx=∫f(x)dx±∫g(x)dx #Аналог-но св.З#
Методы нахожд. неопр. интеграла
Состоит в том,
что при вычислении интеграла
Пусть
u
явл функцией от Х (u=
- формула замены переменных. Заметим,
что когда речь идет о ф-ле (1) естественно
предполагается существование
Докажем формулу (1). 1)Вычислим производные C одной стороны:
Т.к. du=φ’(x)dx С другой стороны d( Т.о. обе части ф-лы имеют один и тот же диф-ал, и поэтому выражают собой одно и то же семейство первообр для ф-ции f(u). Это и док-ет ф-лу в том смысле, что правая и левая части её могут отл между собой разве лишь на константу# интеграл стоящий в левой части равенства (1) существует. Если интеграл существует, то
Пр-р
2. Интегрирование по частям. Этот метод основан на св-ве дифференциала функции. В его основе лежит ф-ла вычисления дифференциала произведения 2х функций Пусть u и v - дифференцируемые ф-ии от х. Тогда d(uv)=udv+vdu, откуда udv=d(uv)-vdu. Проинтегрировав обе части равенства, получим ∫udv=uv-∫vdu. Пр-р ∫xex dx=[u=x, dv=ex, du=dx, v=ex]=xex-∫exdx= xex- ex= ex(x-1) ШКМ: Понятие первообразной есть на всех уровнях обучения математики, но не дается термина неопределенного интеграла (только в углубленном изучении). Само понятие первообразной возникло из практики. Решение задач на нахождение пути по скорости, это задача и привела к возникновению понятия.
|
Вопрос 9. Определенный интеграл и его свойства. Пусть ф-ия f(x) задана в некотором промежутке [a, b]. Разобьем этот промежуток на n произвольных частей x0=a<x1<x2<…<xi<xi+1<…<xn=b. В рез-те получим частичные отрезки [xi, xi+1]
Обозначим Δxi
– длина частичного отрезка. Наибольшую
разность Δxi=xi+1-xi
(i=0,
1, …, n-1)
будем обозначать λ. Возьмем в каждом
из частичных промежутков [xi,
xi+1]
произвольную точку x=ξi,
что xi≤ξi≤xi+1
и составим сумму
Опр.
Если
существует конечный предел
Если такой предел сущ-т, то ф-я f(x) наз интегр-ая по Риману, а интеграл наз опред интегралом Римана. Опред инт-л это предел, след-но это число. !mi и Mi соотв-но нижн и верх границы ф-ии f. s=сумма от i=0 до n-1 (mi∆xi), S=сумма от i=0 до n-1 (Mi∆xi) – нижняя и верхняя инт-ая сумма Дарбу. Св-ва сумм Дарбу: 1)s<S независимо от разбиения, 2)при измельчении суммы Дарбу нижняя только увеличивается, верхняя только уменьшается 3)интегр сумма всегда распол-на м/у s и S 4)sup s=I*-нижний интеграл Дарбу, inf S=I*-верхний интеграл Дарбу. При их совпадении определенный интеграл сущ-ет. Например, для у=const. Опр Крив. тапецией наз плоская фигур, сверху ограниченная гр функции y=f(x), такой что
f(x)
Геометр.смысл
Рассмотрим задачу об опр площади кр
трапеции, ограниченной сверху кривой
у=f(х),
где f(х)-
положит-ая непрер-ая ф-ия, заданная на
отр[а, b].
Площадь этой трапеции была вычислена
как предел, суммы
Необх усл инт-ти ф-ции: Если ф-ия f(x) интегрируема на отр [а, b], то она ограничена на этом отрезке. Суммы Дарбу. ! f(x) ограничена на [a;b] и хi – произвольное разбиение этого отрезка. Т.к ф.ограничена на отрезке, то она ограничена и на любом промежутке [xi-1;xi], а поэтому у ф-и f(x) существует точная нижняя грань mi и точная верхняя грань Mi на промежутке [xi-1;xi].
Обозначение.
Введем понятия верхней и нижней сумм. Опр. Суммы
и
будем называть соответственно нижней и верхней суммами ф-и f(x) для данного разбиения {xi} отрезка [a;b]. s<S не зависимо от обстоятельств. Свойства сумм Дарбу. 1) f(x) ограничена на [a;b] => s, S определены. Док-во:
f
– огр. => Е(f)
– огр.
=>(по
т.)
2) при измельчении разбиения, нижняя интегральная сумма может только увеличиваться, а верхняя только уменьшаться. Док-во: (для нижних сумм)
Разбиение τ s
=
Разбиение
(inf совпали)
n – кол-во точек. Сумма Дарбу зависит от количества точек Нижняя сумма Дарбу будет увеличиваться. # При стремлении разбиения к 0, кол-во точек в разбиении увел. (происходит из мельчайшего разбиения), тем самым нижняя сумма Дарбу увеличивается. Свойства определенного интеграла.
1.
2.
3.
4.
5.
f
≥0 на [a,
b],
a<b,то
6.Пусть f(x) и g(x) интегр на [a,b], f(x)≥g(x) для любого х из [a,b], тогда
7. Пусть ф-ция f(x) непрерывна на [a,b], a<b. Тогда:
8.
Пусть f(x)
интегр на [a,b],
a<b.
Причём
Теорема о среднем: Если
f
непрерывна на
Док-во: Т.
К. функция непрерывна на [a;b]
то по 2 теореме ВШ она принимает свое
наибольшее и наименьшее значения в М
и m
соответственно, т. е. справедливо
тогда
по 2 теореме БК
Пусть a>b, тогда применим теорему о среднем:
ШКМ:
Интеграл
вводится для непрерывной на
|



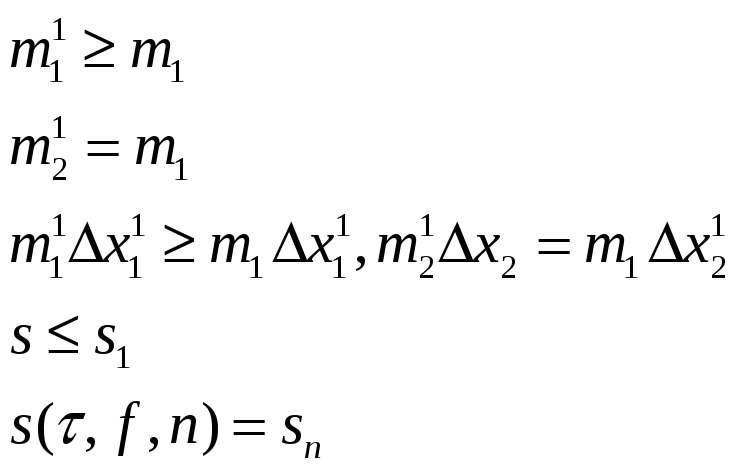
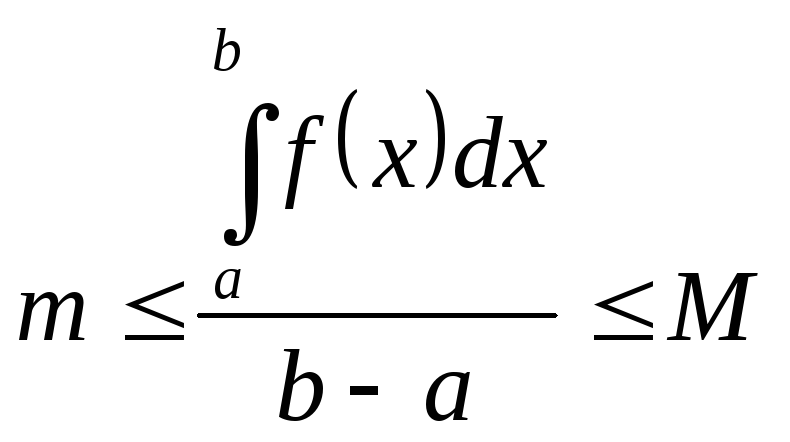 Пусть
Пусть

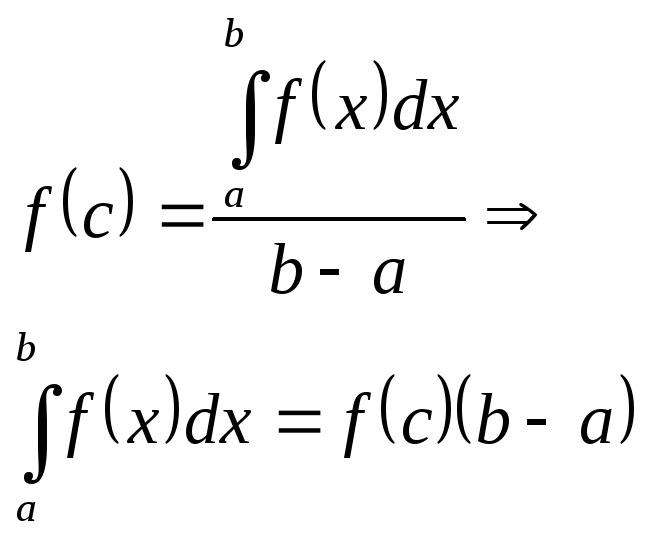
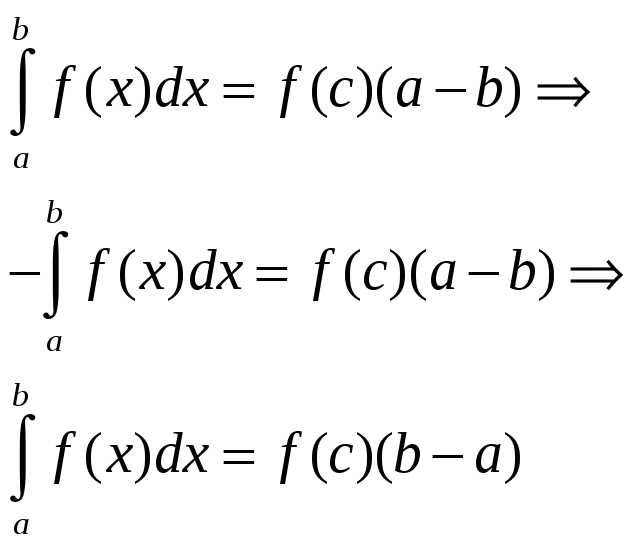 #
#