|
Вопрос
10. Интегрируемость непрерывной функции.
Формула Ньютона-Лейбница.
Теорема
(достаточное условие интегрируемости).
Если фун.f
непрерывна на
 ,
то она интегрируема на этом отрезке. ,
то она интегрируема на этом отрезке.
По
т. Кантора (если фун. непрерывна на
[a;b],
то она равномерно-непрерывна на этом
отрезке) f
непрер. на [a;b],
→равномерно-непрерывна на этом
отрезке. Значит,

 и
таких, что и
таких, что
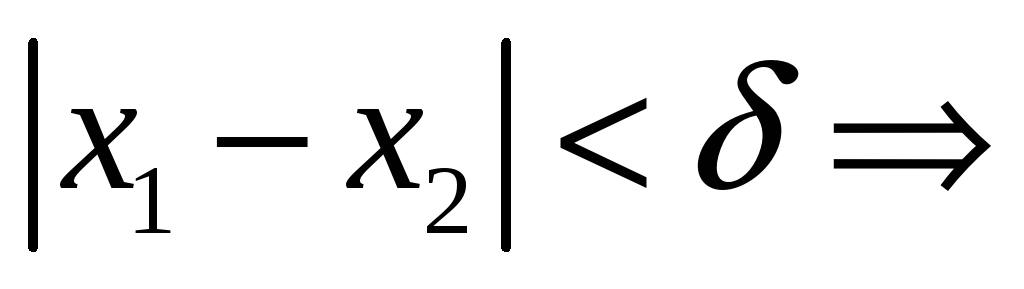
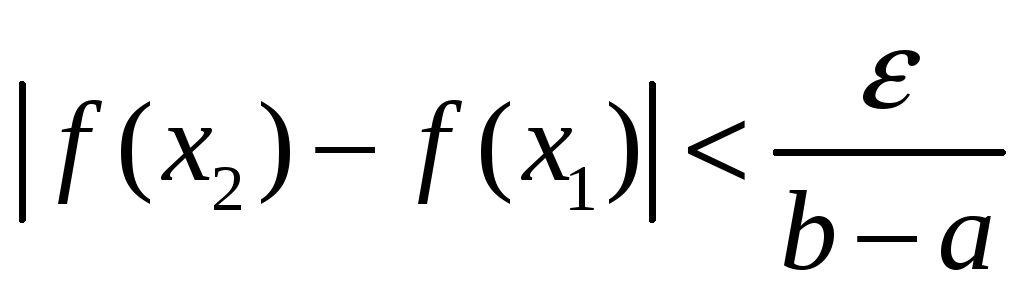 (1) Разобьем отрезок
[a;b]
произвольным образом на части
(1) Разобьем отрезок
[a;b]
произвольным образом на части
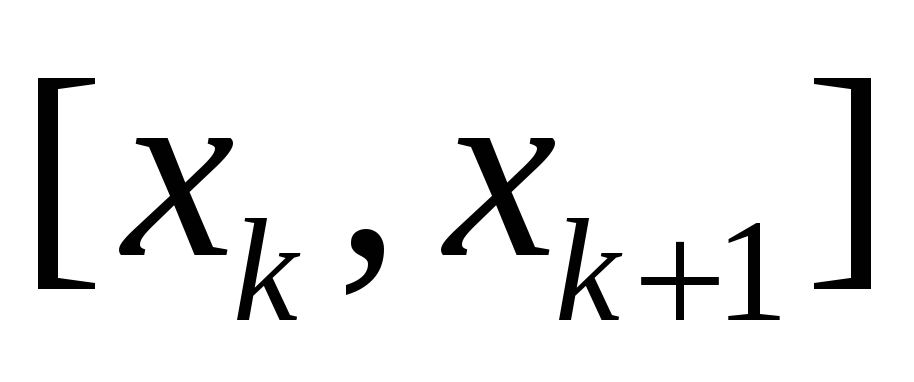 (
(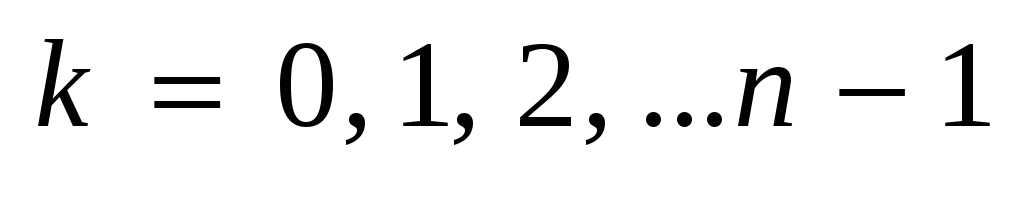 )
с длинами ∆xk
< δ. Пусть этому дроблению отвечают
суммы Дарбу )
с длинами ∆xk
< δ. Пусть этому дроблению отвечают
суммы Дарбу
 и и .
Т.к. ф-я непрерывна на .
Т.к. ф-я непрерывна на
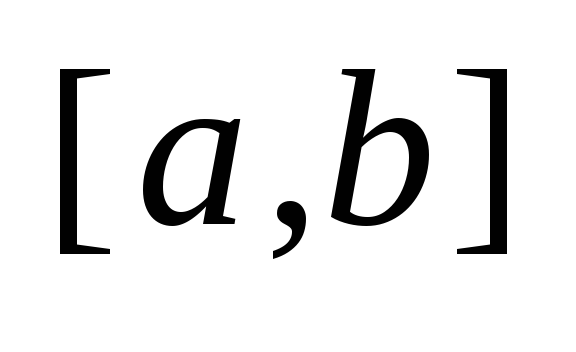 ,
то на каждом ,
то на каждом
 ф-я
ф-я
 принимает свои наиб. и наим. значения
по 2 теореме Вейерштрасса (если
принимает свои наиб. и наим. значения
по 2 теореме Вейерштрасса (если
 непрерывна на
непрерывна на
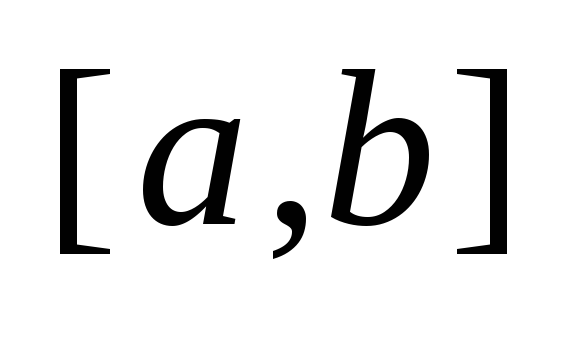 ,
то она на этом отрезке принимает свои
наибольшее и наименьшее значения). ,
то она на этом отрезке принимает свои
наибольшее и наименьшее значения).
След-но
сущ. точка ,
такая что ,
такая что
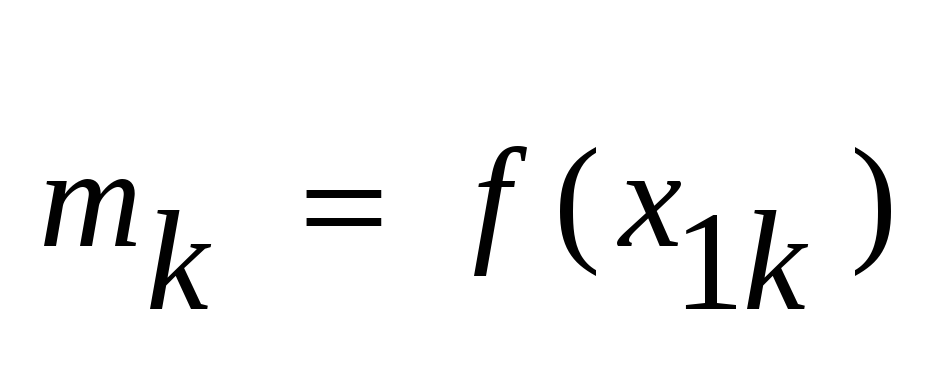 ,
и сущ-ет точка ,
и сущ-ет точка
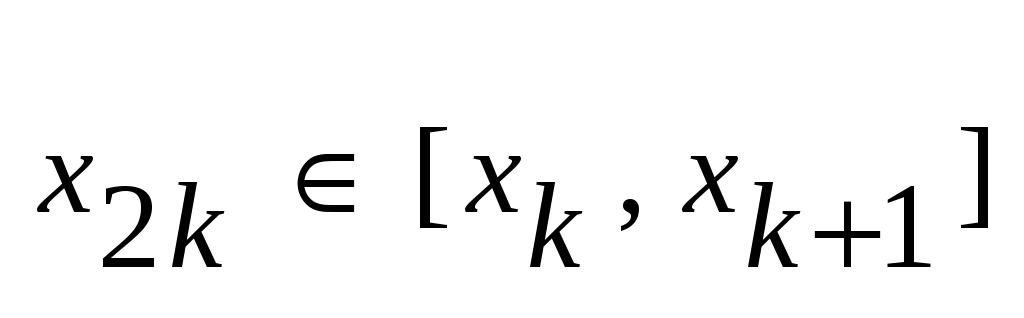 ,
такая что ,
такая что ,
где ,
где
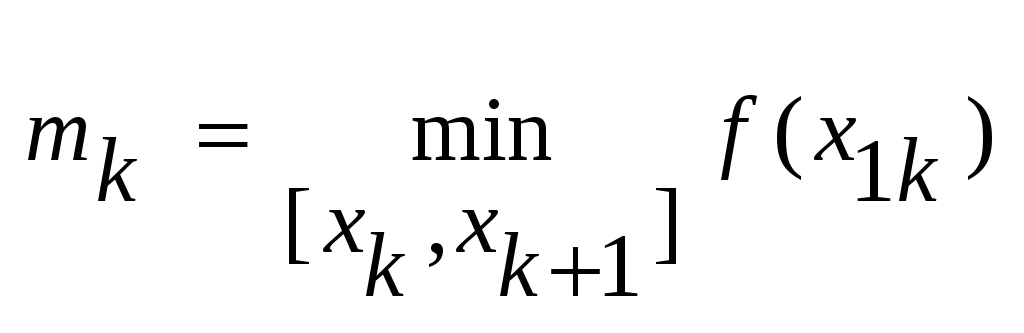 , ,
 .Тогда
в силу нер-ва (1) будем иметь: .Тогда
в силу нер-ва (1) будем иметь:
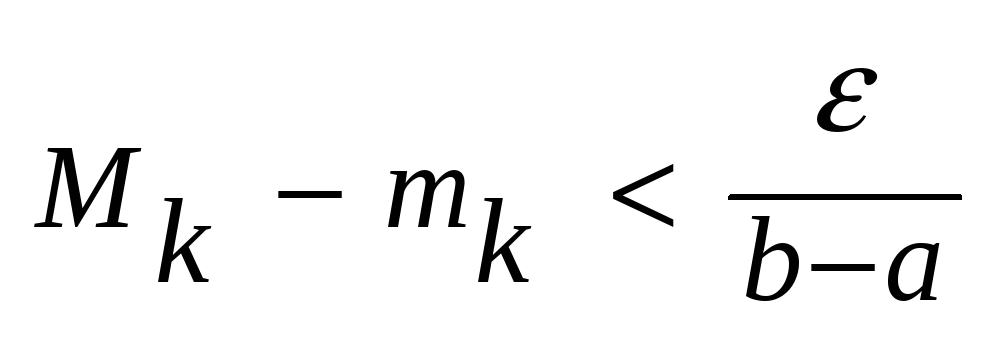 ( (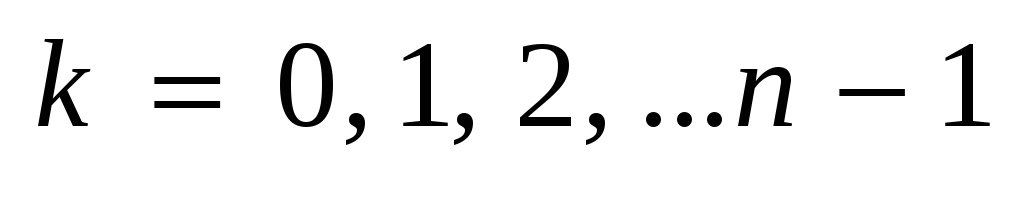 ),
откуда получаем: ),
откуда получаем:
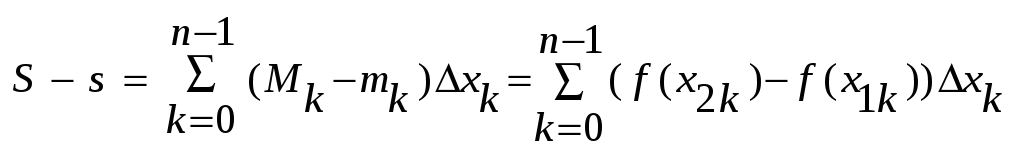
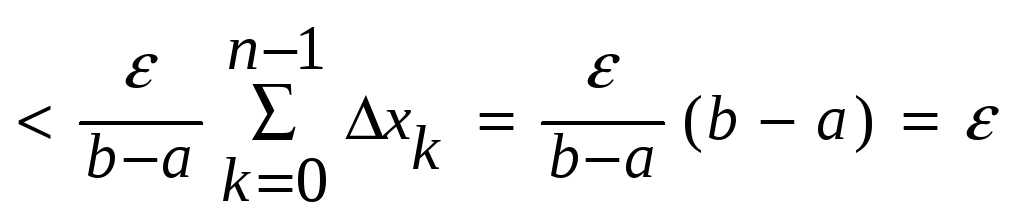
Т.о.
для произвольного ε>0 произвели
дробление отрезка на
 длина
каждого из которых < δ и показали
что в этом случае S-s
< ε. А это означает, что длина
каждого из которых < δ и показали
что в этом случае S-s
< ε. А это означает, что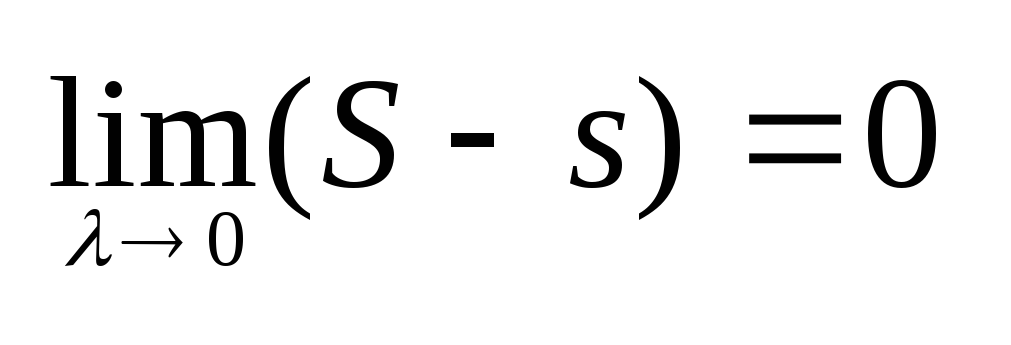 .Значит
f(x)
интегр на [a,b].
# .Значит
f(x)
интегр на [a,b].
#
Интеграл
с переменным верхним пределом.
Опр.
Пусть f(t)
непрер на[a,b].
f(t)
непрер на [a,x],
след-но интегр на [a,x].
Тем самым на отр [a,b]
опр ф-ция F(x)=∫xaf(t)dt,
кот наз-ся инт
с перем вер пределом.
Рассм-м
фун.
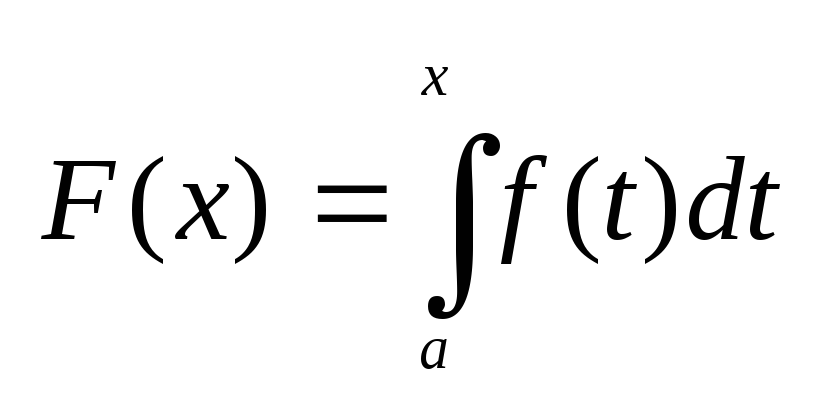 (2), где x-переменный
верхний предел, t-переменная
интегрирования. Если фун.
(2), где x-переменный
верхний предел, t-переменная
интегрирования. Если фун.
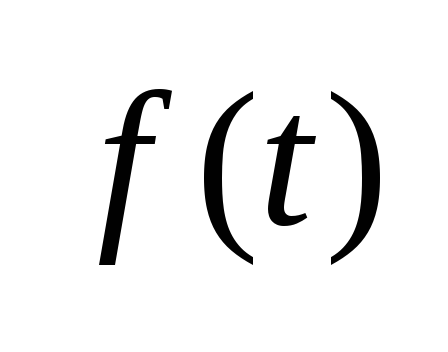 непрер. на [a;b],
то она также будет непрер. и в пром-ке
[a;x],
где a
< x
≤ b,
так что интеграл (2) сущ-ет, и фун. F(x)
имеет смысл рассм-ть для всех точек
замкнутого промежутка [a;b],
кроме точки x=a,
в кот. интеграл (2) пока теряет смысл.
В самом деле, определение определенного
интеграла мы дали только для случая
когда пределы интегрирования не равны
между собой, т.е. когда a
≠ b.
Чтобы не исключать случая x=a,
придадим определенный смысл выражению
непрер. на [a;b],
то она также будет непрер. и в пром-ке
[a;x],
где a
< x
≤ b,
так что интеграл (2) сущ-ет, и фун. F(x)
имеет смысл рассм-ть для всех точек
замкнутого промежутка [a;b],
кроме точки x=a,
в кот. интеграл (2) пока теряет смысл.
В самом деле, определение определенного
интеграла мы дали только для случая
когда пределы интегрирования не равны
между собой, т.е. когда a
≠ b.
Чтобы не исключать случая x=a,
придадим определенный смысл выражению
 .
Применяя теорему о среднем к (2) (если
фун. .
Применяя теорему о среднем к (2) (если
фун.
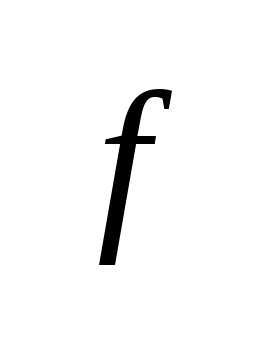 непрерывна на [a;b],
то на этом отрезке сущ-ет c,
что
непрерывна на [a;b],
то на этом отрезке сущ-ет c,
что
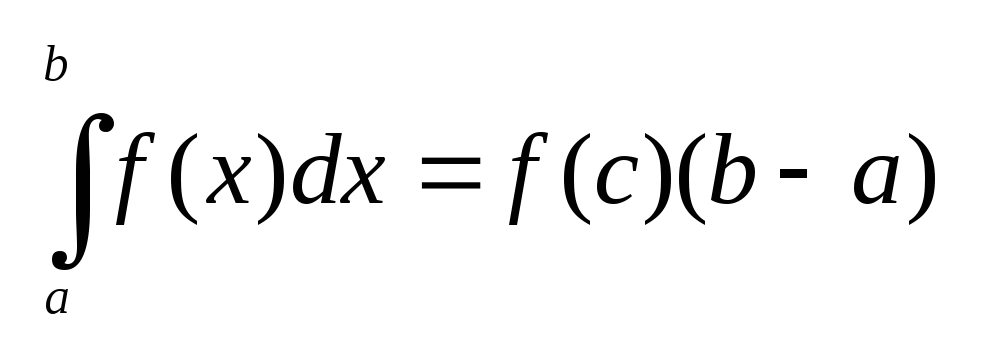 )
находим: )
находим:
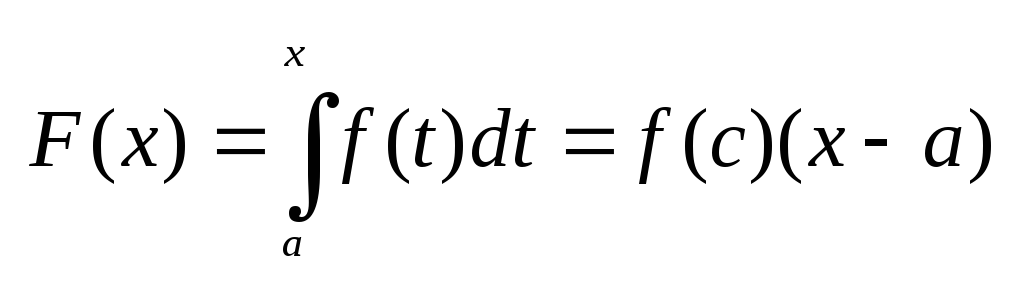 ,
где c
содержится в [a,x].
Перейдем к пределу в этом рав-ве при
xa ,
где c
содержится в [a,x].
Перейдем к пределу в этом рав-ве при
xa
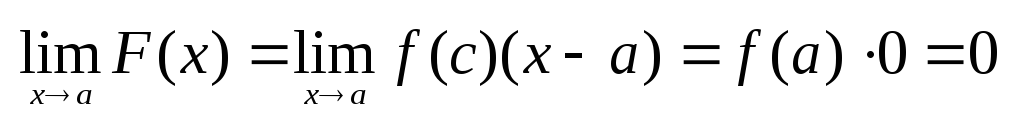 .
В связи с этим естественно .
В связи с этим естественно
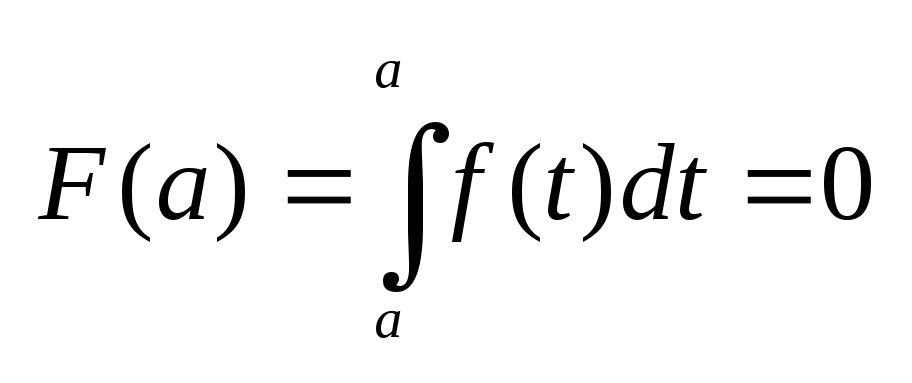 . .
ф-ла Ньютона-Лейбница
Мы
показали что любая непр на [a,b]
ф-ция f(x)
имеет на этом отрезке первообр. равную
опр интегралу. Обозн ч/з
F(x)
ещё одну первообр. Следов
(1)
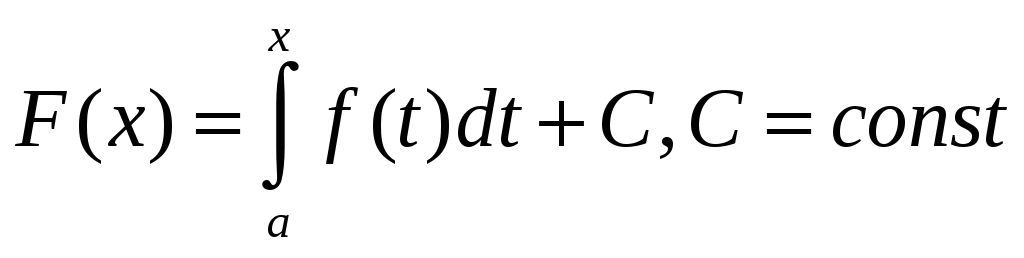
Найдём
постоянную С. Пусть х=а.
Тогда

Подставим
С в рав-во (1)

!x=b
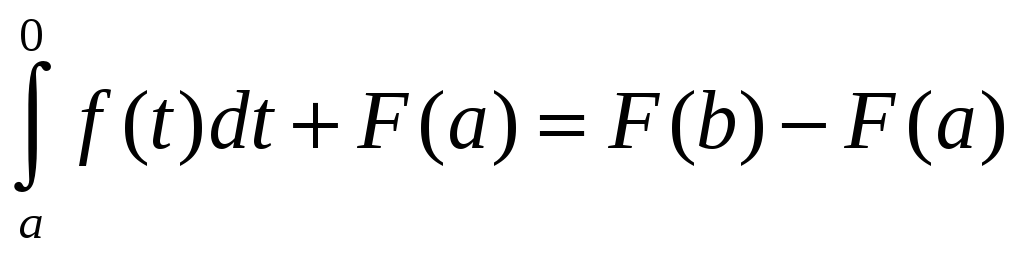 , ,
Где
F(t)
первообр для f(t).
Если
 непрерывная [a;b],
то справедлива ф-ла
непрерывная [a;b],
то справедлива ф-ла
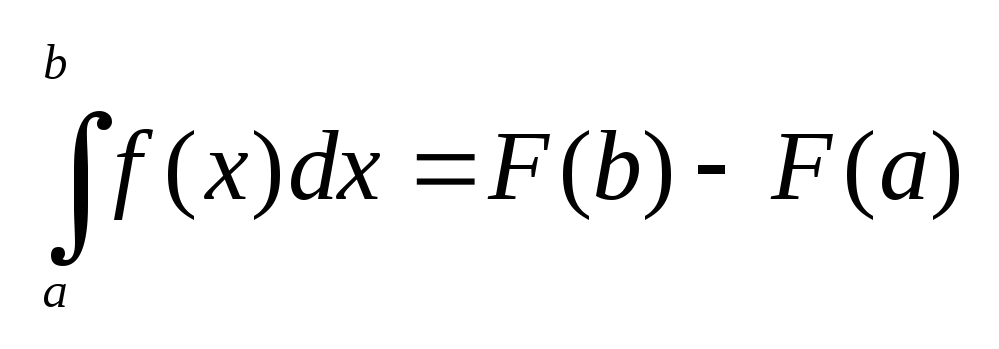 ,
где F
-первообразная фун. f
на [a;b]. ,
где F
-первообразная фун. f
на [a;b].
Пример:
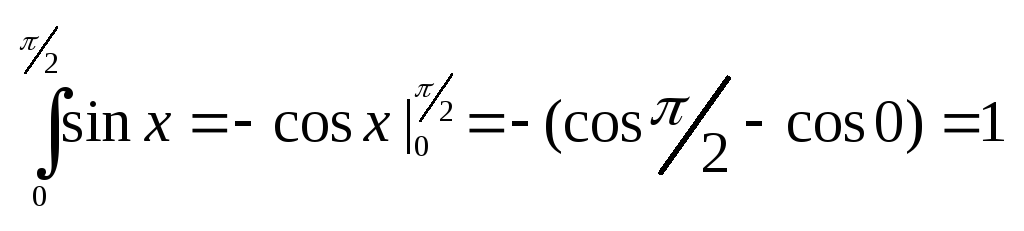 . .
Значение
ф-лы: Это
мощнейший аппарат вычисления интеграла.
Эта формула прорыв в интегральном
исчислении, она позволила решать
многие задачи естествознания, физики,
техники. Это великое открытие математики.
В
ШКМ 1). В
действующем стандарте определение
изучается в 11 кл. вводится как предел
интегральных сумм; 2) вводится понятие
неопред. интеграл, опред. интеграл.
Рассматривается
формула Н-Л и используется для вычисления
интегралов.
|
Вопрос
11. Площадь плоской фигуры. Вычисление
площадей с помощью определенного
интеграла.
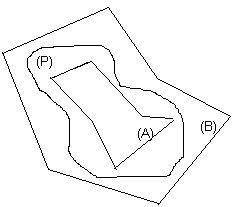 Пусть
дана произв плоская фигура (P),
огран замкнутой кривой, которую наз-ют
границей или контуром данной фигуры.
Рассм-м всевозможные многоуг-ки (А)
площади S(А),
целиком содержащиеся в (Р), и многоуг-ки
(В)площади S(В),
целиком содержащие в себе (Р). Для
площадей этих многоуг-ов будем всегда
иметь S(A)
≤ S(B).
Отсюда следует, что мн-во чисел {A}
ограничено сверху, например, любым
числом В. Пусть
дана произв плоская фигура (P),
огран замкнутой кривой, которую наз-ют
границей или контуром данной фигуры.
Рассм-м всевозможные многоуг-ки (А)
площади S(А),
целиком содержащиеся в (Р), и многоуг-ки
(В)площади S(В),
целиком содержащие в себе (Р). Для
площадей этих многоуг-ов будем всегда
иметь S(A)
≤ S(B).
Отсюда следует, что мн-во чисел {A}
ограничено сверху, например, любым
числом В.

{S(A)}
ограниченно сверху =>
это
мн-во имеет конечную точную верхнюю
границу
 , ,
 - нижняя площадь, и
- нижняя площадь, и
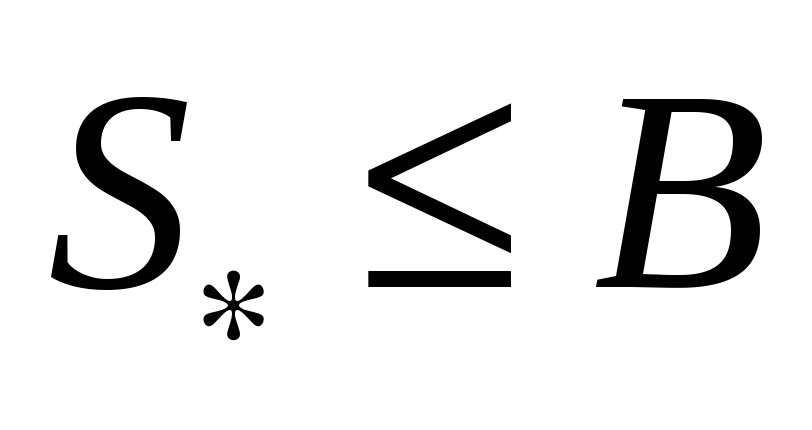 а
мн-во чисел {B}
ограничено снизу числ а
мн-во чисел {B}
ограничено снизу числ
{S(В)}
ограниченно снизу =>
это
мн-во имеет конечную, точную нижнюю
границу
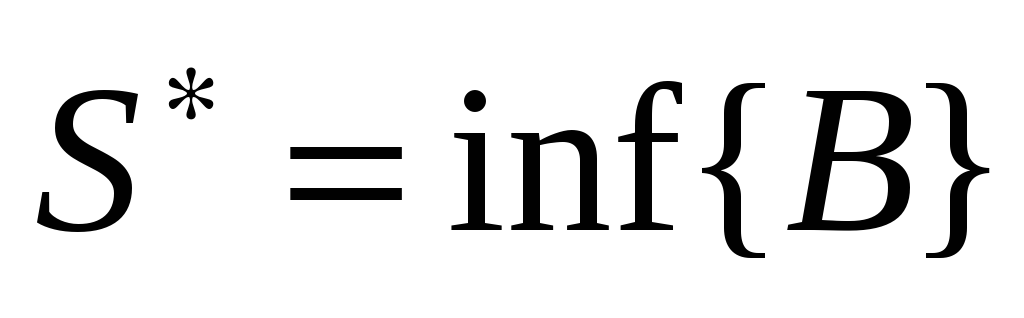 ,
причем ,
причем
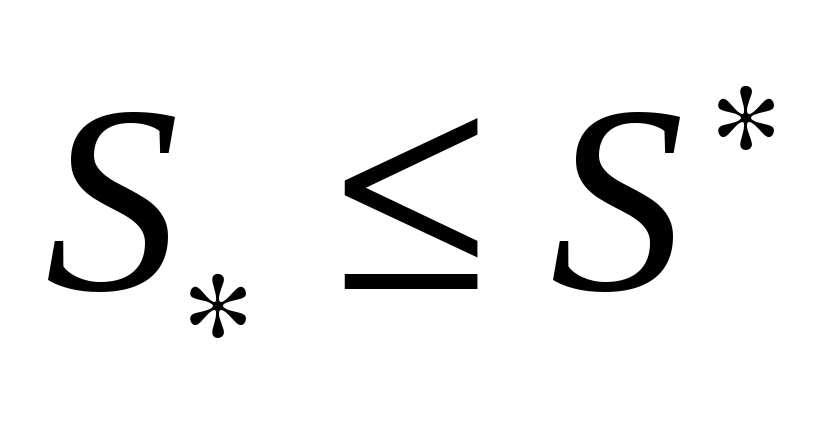 . .
Опр.
Если обе границы
 и
и
 равны друг другу:
равны друг другу:
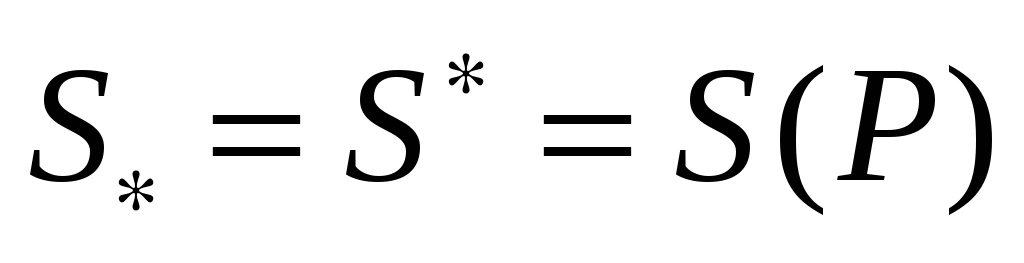 ,
то их общее значение (Р) наз-ся площадью
фигуры (Р), а саму фигуру в этом случае
наз-ют квадрируемой. ,
то их общее значение (Р) наз-ся площадью
фигуры (Р), а саму фигуру в этом случае
наз-ют квадрируемой.
Площадь
криволинейной трапеции.
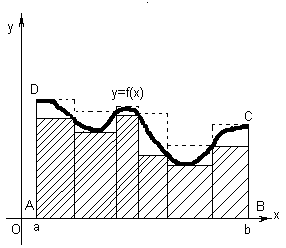
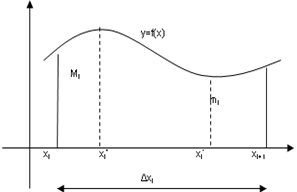
Пусть
нам дана криволинейная трапеция ABCD.
Разобьем промежуток [a;b]
на n
произвольных частей точками
 .
Восстанавливаем перпендикуляры к оси
абсцисс в этих точках. Обозначим через
mi,
Mi
соответственно наим. и наиб. значения
фун. f(x)
на частичном пром-ке .
Восстанавливаем перпендикуляры к оси
абсцисс в этих точках. Обозначим через
mi,
Mi
соответственно наим. и наиб. значения
фун. f(x)
на частичном пром-ке
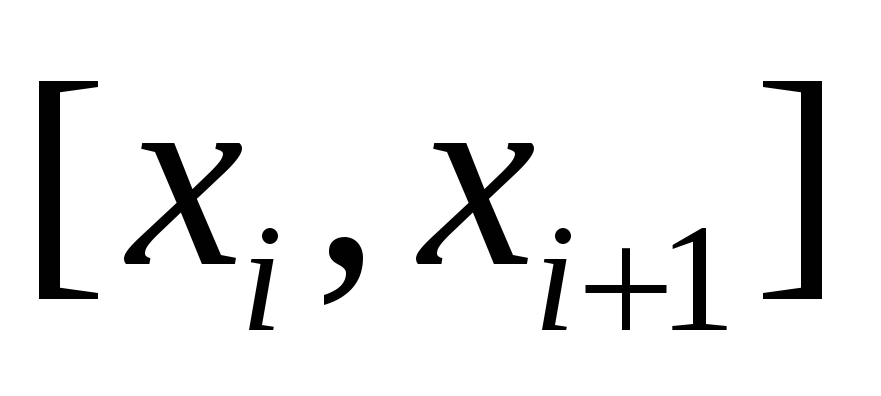
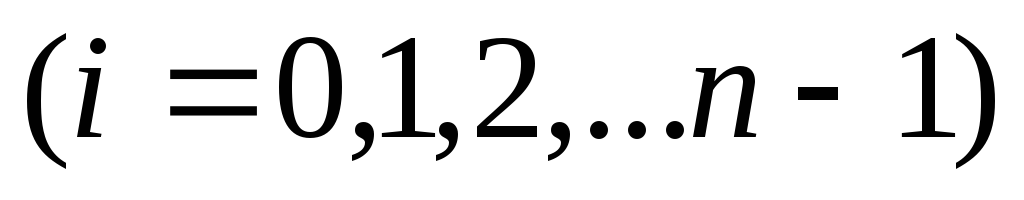 .
В силу непрер. f(x)
по 2
теор. Вейерштрасса (если f
непрерывна на .
В силу непрер. f(x)
по 2
теор. Вейерштрасса (если f
непрерывна на
 ,
то она на этом отрезке принимает свои
наиб.и наим. значения) такие значения
сущ-ют. ,
то она на этом отрезке принимает свои
наиб.и наим. значения) такие значения
сущ-ют.
Будем
искать площади:
 , ,
 ,
где ,
где
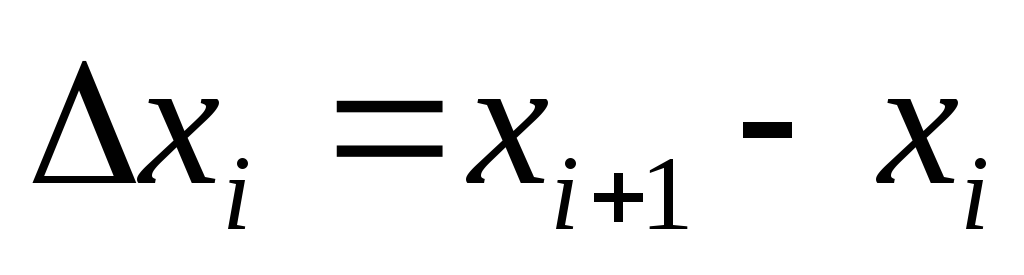 .
Сумма Дарбу s,
очевидно представляет собой пл-дь
ступенчатой фигуры (входящего
многоуг-ка), целиком содержащийся в
кривол. трапеции ABCD;
сумма Дарбу S
выражает пл-дь ступенчатой фигуры
(выходящего многоуг-ка), содержащей
эту кривол. трапецию. Т.к. для непрер.
фун. f(x)
суммы Дарбу s
и S
яв-ся просто наим. и наиб. Из интегральных
сумм, то по теор. о сущ-нии опред.
интеграла обе суммы при .
Сумма Дарбу s,
очевидно представляет собой пл-дь
ступенчатой фигуры (входящего
многоуг-ка), целиком содержащийся в
кривол. трапеции ABCD;
сумма Дарбу S
выражает пл-дь ступенчатой фигуры
(выходящего многоуг-ка), содержащей
эту кривол. трапецию. Т.к. для непрер.
фун. f(x)
суммы Дарбу s
и S
яв-ся просто наим. и наиб. Из интегральных
сумм, то по теор. о сущ-нии опред.
интеграла обе суммы при
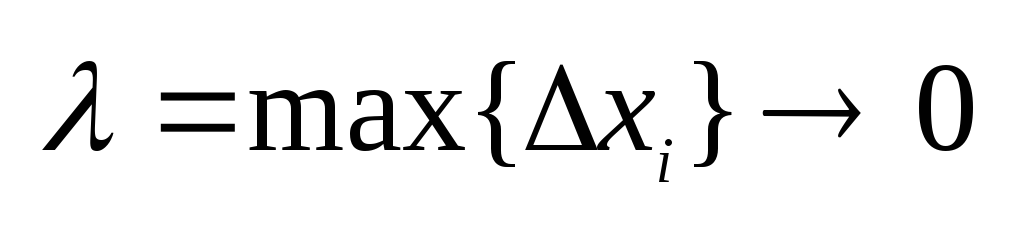 имеют своим общим пределом интеграл
имеют своим общим пределом интеграл
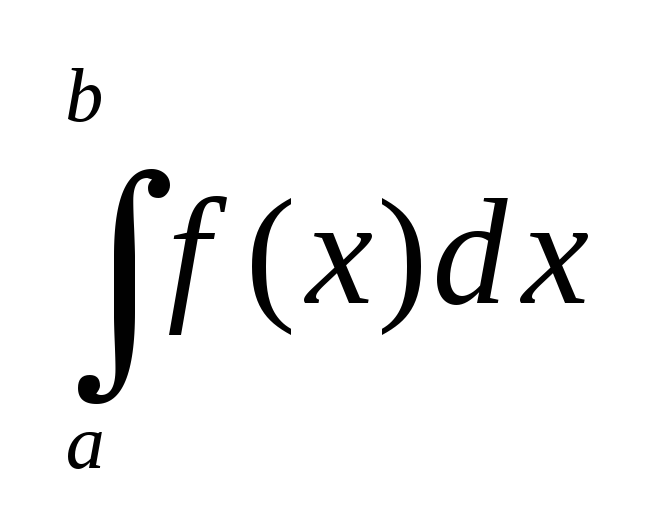 : :
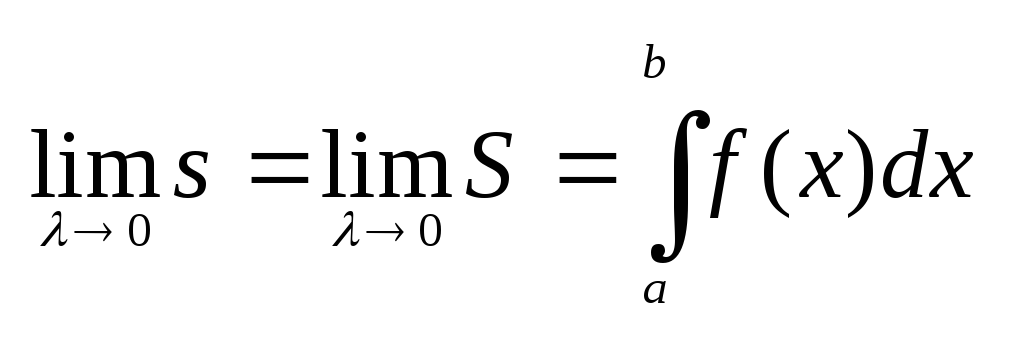 откуда и следует, что пл-дь S{Р}
данной кривол. трапеции сущ-ет и равна
этому же интегралу:
откуда и следует, что пл-дь S{Р}
данной кривол. трапеции сущ-ет и равна
этому же интегралу:
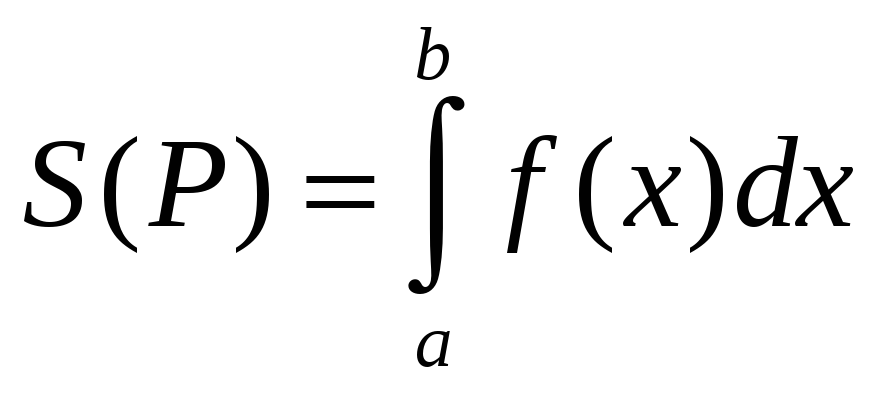 . .
Общий
случай выч-ния пл-дей плоских фигур
Р ассм-м
случай, когда некоторые части кривой ассм-м
случай, когда некоторые части кривой
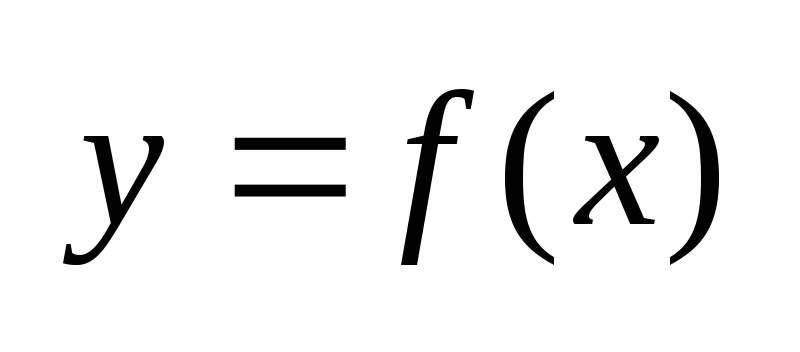 нах-ся над осью ОХ, а др. под осью ОХ. В
этом случае интеграл
нах-ся над осью ОХ, а др. под осью ОХ. В
этом случае интеграл
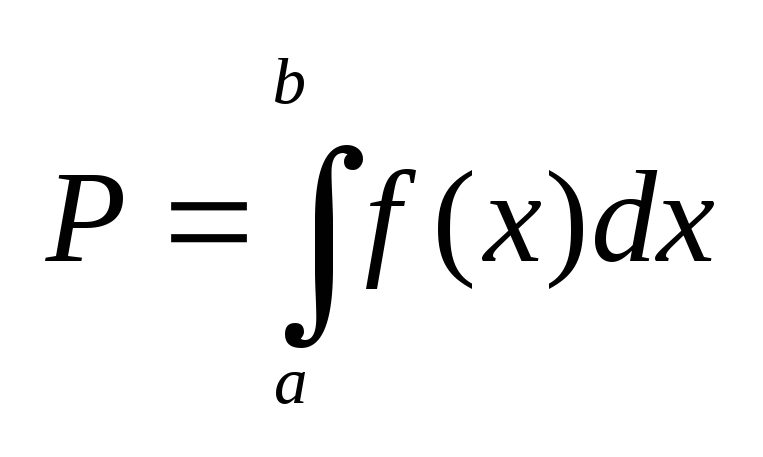 и по абсолютной величине не дает уже
пл-ди всей заштрихованной фигуры, а
представляет собой алгебр-ую сумму
пл-дей тех частей фигуры, кот. расположены
над осью ОХ и тех ее частей кот. нах-ся
под осью ОХ. Поэтому пл-дь всей фигуры
в данном случае выразится ф-лой
и по абсолютной величине не дает уже
пл-ди всей заштрихованной фигуры, а
представляет собой алгебр-ую сумму
пл-дей тех частей фигуры, кот. расположены
над осью ОХ и тех ее частей кот. нах-ся
под осью ОХ. Поэтому пл-дь всей фигуры
в данном случае выразится ф-лой
 . .
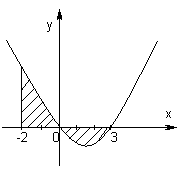
Пример:
Найти пл-дь
фигуры, огран. параболой
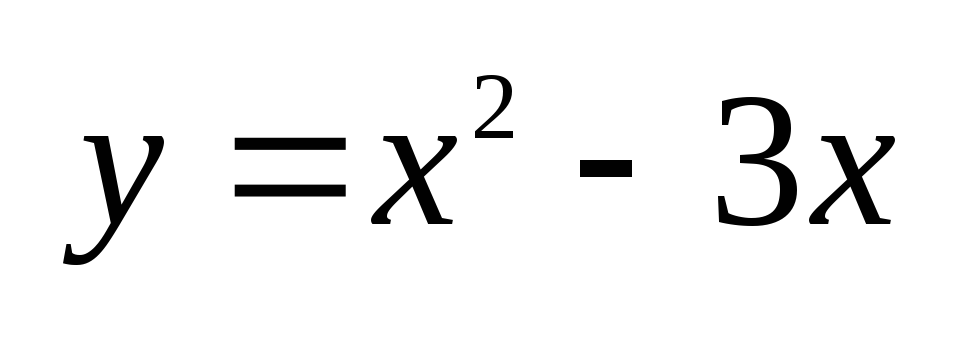 и прямой x=-2
и осью ОХ.
и прямой x=-2
и осью ОХ.
Решение:
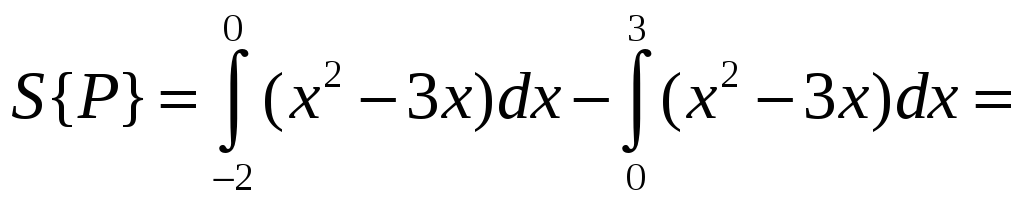

В ШКМ
квадрируемость фигуры не используется,
площадь криволинейной трапеции с
пом-ю интеграла вычисляется.
|
Вопрос
12. Объем тела. Вычисление объемов с
помощью определенного интеграла.
Рассм. множ-во
многогр-ов, вписанных в фигуру. Объёмы
этих многогр-ов обозначим через V
и рассм. Множ-во многогр-ов, которые
содержат данную фигуру: V1.
Множ-во объёмов вписанных многогр-ов
будет ограничен сверху: sup{Q}=V*.
Множ-во объёмов, описанных многогр-ов
будет ограничен снизу inf{Q1}=V1*.
Опр.
Если V*=
V1*=V,
то пространственная фигура наз-тся
кубируемой
и объём
равен V.
Теорема 1:
Для того, чтобы тело имело объём необ.
и достат., чтобы существовали две такие
послед-сти, соответственно входящих
и выходящих многогр-ов {Q}
и {Q1},
объёмы которых имели общий предел
limQ=limQ1=V.
Этот предел и будет объёмом тела.
Теорема 2:
Если для
тела можно построить последовательности,
соотв-но входящих и выходящих кубируемых
тел Tn
и Un,
объёмы которых имели бы общий предел
limTn=Un=V.
Этот предел и будет объёмом тела.
Выч-ние объёмов
тел по их поперечному сечению. Если
рассмотреть поперечные сечения S,
перпендикулярные оси Ox,
то в сечении данной фигуры получится
плоская фигура, площадь которой равна
S(x).
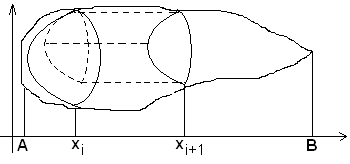
Будем считать
что S(x)
непрерывна. Пусть любая пара сечений,
ортогонально спроектированных на
плоскость, перпендикулярную Ox,
дает проекции целиком лежащие одна
на другой. При этих условиях тело имеет
объём V,
который выражается формулой:
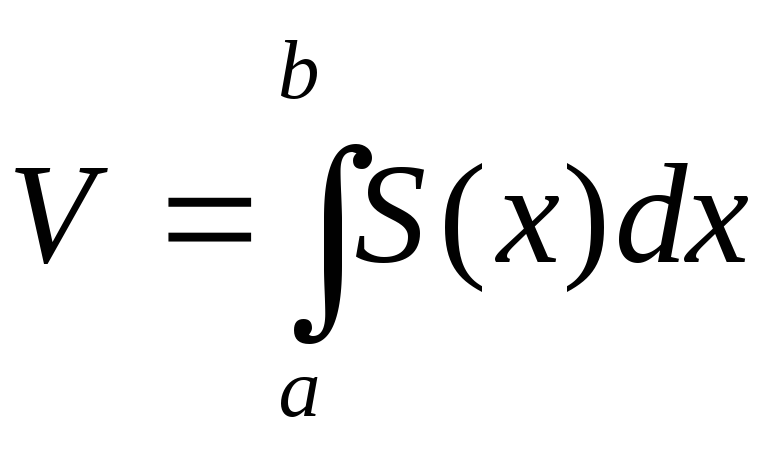 (1),[АВ]
разобьём произвольно на n
частей точками a=x0<x1<…<xi<xi+1<…<xn=b.
Через эти точки проведём плоскости,
перпендикулярные к оси Ox.
Эти плоскости разобьют тело на n
тонких слоёв, толщина каждого из
которого равна величине Δxi=
xi+1-
xi(i=0,1,2,…,n-1).
Рассм. 1-й слой, заключенный между
плоскостями x=xi
и
x=xi+1(i=0,1,2,…,n-1).
Ф-ция принимает макс-ное и мин-ное
значение. Будем считать, что
minS(x)=mi,maxS(x)=Mi
в частичном промежутке [xi,xi+1]-это
будут площади наименьшего и наибольшего
сечения в i-ом
промежутке. 1-й слой содержится м/у
двумя прямыми цилиндрами высоты Δxi,
построенными
на сечениях площади mi
и Mi.
Объёмы
этих цилиндров равны, соответственно
mi
·Δxi
и Mi
· Δxi.
Построив
такие цилиндры для каждого слоя,
получим два ступенчатых тела, одно из
которых состоит из входящих цилиндров,
след-но, содержится в данном теле, а
другое – из выходящих цилиндров и
след-но, содержат данное тело. Объёмы
этих тел соотв-но равны: (1),[АВ]
разобьём произвольно на n
частей точками a=x0<x1<…<xi<xi+1<…<xn=b.
Через эти точки проведём плоскости,
перпендикулярные к оси Ox.
Эти плоскости разобьют тело на n
тонких слоёв, толщина каждого из
которого равна величине Δxi=
xi+1-
xi(i=0,1,2,…,n-1).
Рассм. 1-й слой, заключенный между
плоскостями x=xi
и
x=xi+1(i=0,1,2,…,n-1).
Ф-ция принимает макс-ное и мин-ное
значение. Будем считать, что
minS(x)=mi,maxS(x)=Mi
в частичном промежутке [xi,xi+1]-это
будут площади наименьшего и наибольшего
сечения в i-ом
промежутке. 1-й слой содержится м/у
двумя прямыми цилиндрами высоты Δxi,
построенными
на сечениях площади mi
и Mi.
Объёмы
этих цилиндров равны, соответственно
mi
·Δxi
и Mi
· Δxi.
Построив
такие цилиндры для каждого слоя,
получим два ступенчатых тела, одно из
которых состоит из входящих цилиндров,
след-но, содержится в данном теле, а
другое – из выходящих цилиндров и
след-но, содержат данное тело. Объёмы
этих тел соотв-но равны:
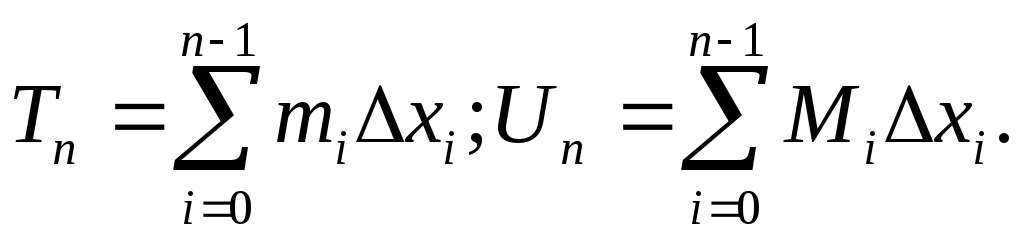 Т.к.
эти суммы являются суммами Дарбу для
непрерывной ф-ции S(x),
то они явл-ся просто наименьшим и
наибольшим из интегральных сумм, тогда
по теореме о существовании опред-го
интеграла обе суммы при λ=max
Δxi→0
имеют своим общим пределом интеграл Т.к.
эти суммы являются суммами Дарбу для
непрерывной ф-ции S(x),
то они явл-ся просто наименьшим и
наибольшим из интегральных сумм, тогда
по теореме о существовании опред-го
интеграла обе суммы при λ=max
Δxi→0
имеют своим общим пределом интеграл
 ,
откуда и следует в силу теоремы 2, что
этот интеграл выражает объём рассм-го
тела. В случае, когда рассм-ное тело
получено вращением некоторой кривой
y=f(x)
вокруг оси Ox,
будут получ-ся круги площади
S(x)=πy2=πf2(x).Подставив
это в (1) получим формулу для вычисления
объёма тела вращения: ,
откуда и следует в силу теоремы 2, что
этот интеграл выражает объём рассм-го
тела. В случае, когда рассм-ное тело
получено вращением некоторой кривой
y=f(x)
вокруг оси Ox,
будут получ-ся круги площади
S(x)=πy2=πf2(x).Подставив
это в (1) получим формулу для вычисления
объёма тела вращения:
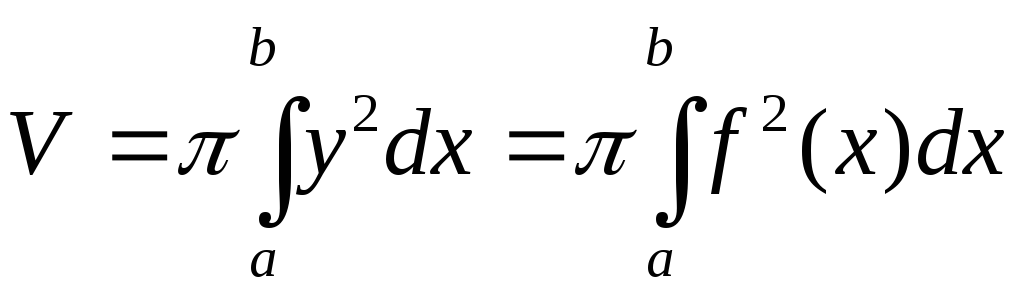
(2). Если кривая,
вращением которой образуется тело
вращения, задана параметрическими
уравнениями x=φ(t),y=ψ(t),α≤t≤β
(3). Где φ(t),
ψ(t)-
функции, удовлетворяют упоминавшимся
ранее требованиям, то, производя замену
переменной в интеграле (2) по формулам
(3), получим:
 (4), где α и β
таковы, что φ(α)=а, φ(β)=b.
Иногда приходится вычислять объём
тела, полученный вращением кривой
x=g(y),
c≤y≤d
вокруг оси Oy.
Объём этого тела вращения выч-ся по
формуле:
(4), где α и β
таковы, что φ(α)=а, φ(β)=b.
Иногда приходится вычислять объём
тела, полученный вращением кривой
x=g(y),
c≤y≤d
вокруг оси Oy.
Объём этого тела вращения выч-ся по
формуле:
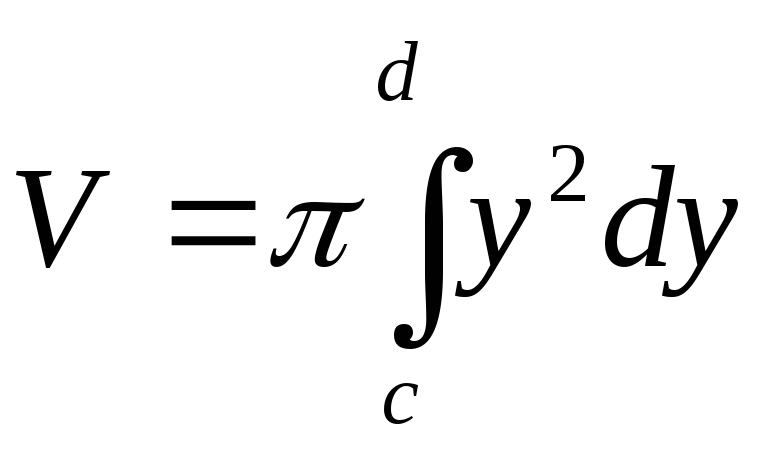 ,
которая выводится аналогично формуле
(2). ,
которая выводится аналогично формуле
(2).
Пример: Выч-ть
объём тела, образ-го вращением одной
арки циклоиды x=a(t-sint),
y=a(1-cost)
вокруг её основания. Объём этого тела
выч-ся по формуле (4), сл-но,

В
ШКМ объёмы
тел с помощью интеграла не вычисляются!!!
(хотя ранее в учебниках Колмогорова
это было)
|



 .
. Пусть
дана произв плоская фигура (P),
огран замкнутой кривой, которую наз-ют
границей или контуром данной фигуры.
Рассм-м всевозможные многоуг-ки (А)
площади S(А),
целиком содержащиеся в (Р), и многоуг-ки
(В)площади S(В),
целиком содержащие в себе (Р). Для
площадей этих многоуг-ов будем всегда
иметь S(A)
≤ S(B).
Отсюда следует, что мн-во чисел {A}
ограничено сверху, например, любым
числом В.
Пусть
дана произв плоская фигура (P),
огран замкнутой кривой, которую наз-ют
границей или контуром данной фигуры.
Рассм-м всевозможные многоуг-ки (А)
площади S(А),
целиком содержащиеся в (Р), и многоуг-ки
(В)площади S(В),
целиком содержащие в себе (Р). Для
площадей этих многоуг-ов будем всегда
иметь S(A)
≤ S(B).
Отсюда следует, что мн-во чисел {A}
ограничено сверху, например, любым
числом В.

 ассм-м
случай, когда некоторые части кривой
ассм-м
случай, когда некоторые части кривой


