7.9 Теоретические распределения в анализе вариационных рядов

Для аппроксимации (выравнивания) эмпирических кривых распределения и сопоставления их с теоретическими в статистике часто пользуются нормальным распределением, функция которого равняется

.

(7.75)

где - ордината кривой нормального распределения;

- стандартизованное отклонение;

и- математические постоянные;

- варианты вариационного ряда;

- их средняя величина;

- среднее квадратическое отклонение.

Нормальное распределение полностью определяется двумя параметрами - средней арифметической () и средним квадратическим отклонением. Подчиненность закону нормального распределения проявляется тем точнее, чем больше случайных величин действуют вместе. Если ни одна из случайно действующих причин по своему действию не окажется преобладающей над другими, то закон распределения очень близко подходит к нормальному.

Такая закономерность проявляется, например, в распределении отклонений в производственном процессе при нормальном уровне организации и технологии, в распределении населения определенного возраста по размеру обуви и т.д.

Часто возникают распределения, хотя и не отвечающие строго нормальному распределению, но имеющие с ним сходство. Такие сходные черты часто обусловлены тем, что крайние значения вариантов, близкие к и, встречаются много реже, чем серединные.

Рассмотрим некоторые свойства кривой нормального распределения:

• - функция нормального распределения - четная, т.е.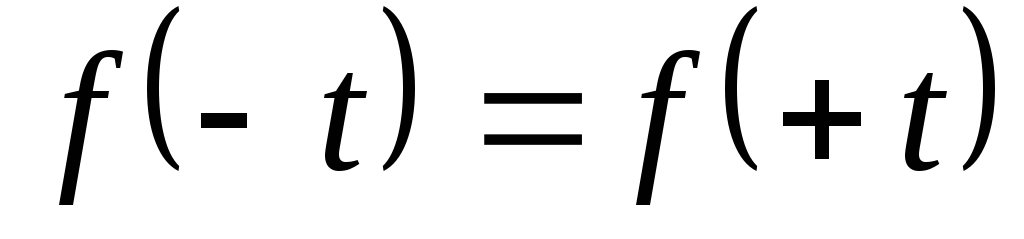. Следовательно, изображающая ее кривая распределена симметрично относительно оси ординат, т.е.;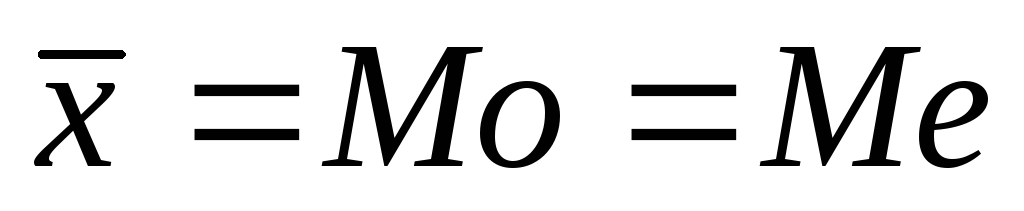

• функция имеет бесконечно малые значения при 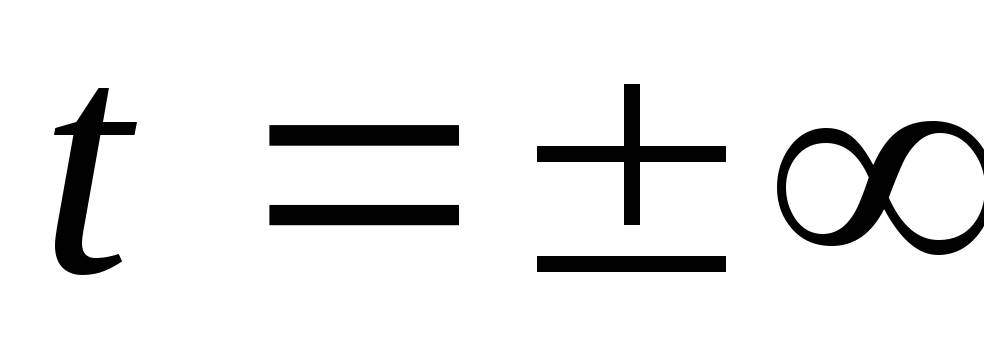. Это означает, что ветви кривой удалены в бесконечность и асимптотически приближаются к оси абсцисс. При этом чем больше значения признака отклоняются от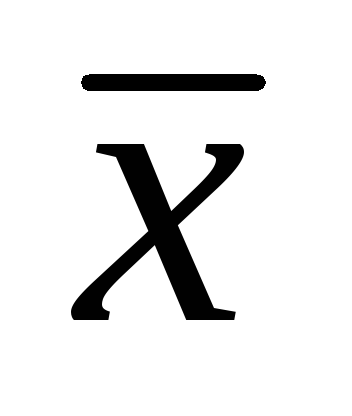, тем реже встречаются;

• функция имеет максимум при 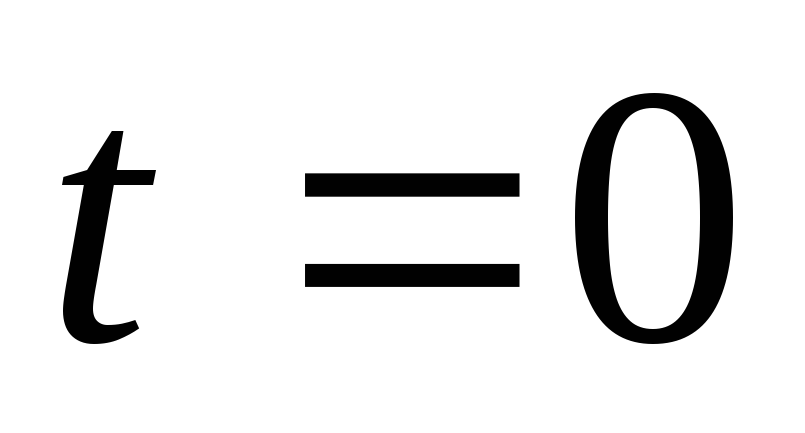.Отсюда следует, что модального значения кривая достигает приили при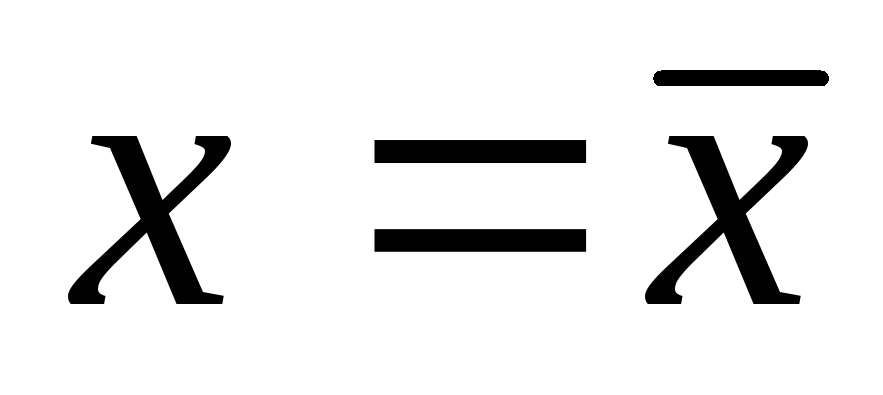. Величина максимума составляет;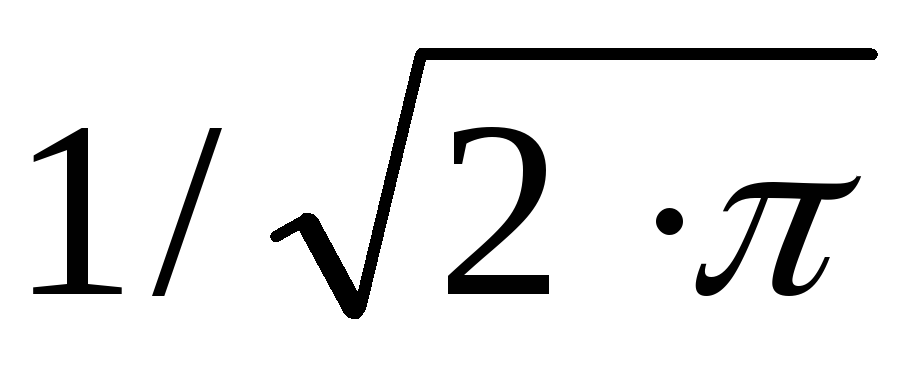

• при 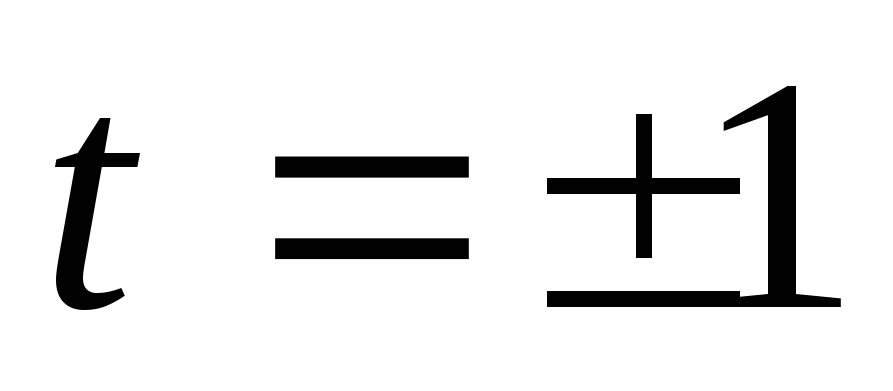функция дает точки перегиба. Следовательно, при отклонении значений признака (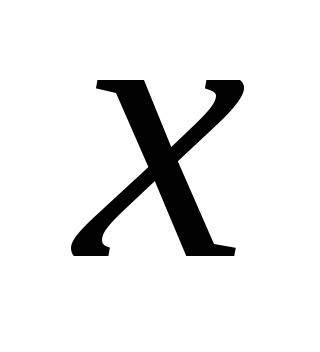) от среднего значения (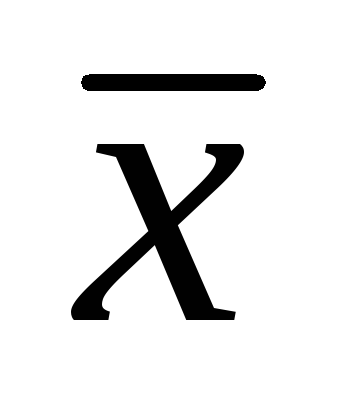) в положительном и отрицательном направлениях на одно стандартное (нормированное) отклонение (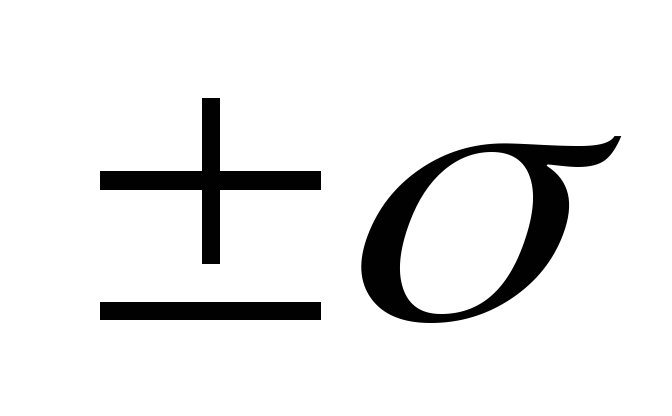от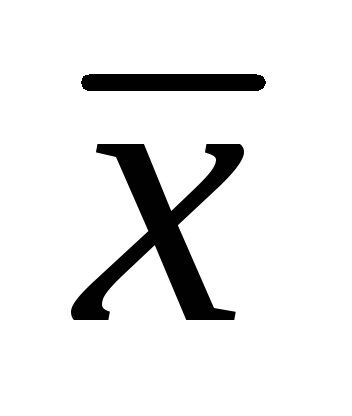) кривая дает переход от выпуклости к вогнутости;

• если случайная величина представляет сумму двух независимых случайных величин, следующих каждая нормальному закону, то она тоже следует нормальному закону;

• площадь между кривой и осью равна единице, как интеграл Пуассона.

Для расчета частот нормального распределения необходимо использовать формулу плотности вероятности:

.

(7.76)

Чтобы прийти к частотам нормального распределения необходимо выразить их через.

Для удобства вычислений вероятностей случайные величины нормируются, а затем используются заранее табулированные значения плотности функции распределения нормированной случайной величины. Первый множитель такой функции - величина постоянная для данного распределения. Во втором множителе выражение обозначим через тогда получим:

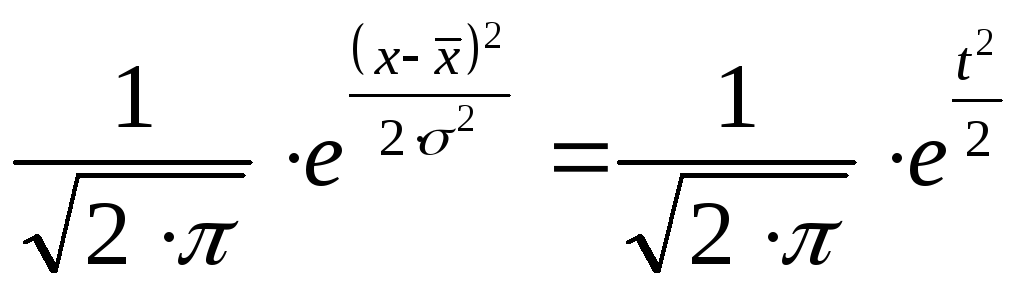
Полученную функцию от обозначим :

.

(7.77)

В математической статистике существуют специальные таблицы для любых значений (приложение 8).

Таким образом, очень легко рассчитать, определив для каждого значения варианта величину и найдя по таблицам соответствующие . Умножив на постоянный для всех частот множитель, получим теоретические частоты нормального распределения.

Далее сравниваются полученные с фактическими частотами , строятся графики полученных частоти фактических .

В то же время нельзя не отметить, что сопоставление графика эмпирических частот с теоретическими в целях определения соответствия эмпирического распределения нормальному позволяет оценивать эти расхождения только субъективно. Объективная характеристика соответствия может быть получена с помощью особых статистических показателей - критериев согласия. Известны критерии согласия К. Пирсона (хи-квадрат), В.И. Романовского, А.Н. Колмогорова и Б.С. Ястремского.

Критерий согласия Пирсона ()вычисляется по формуле:

.

(7.78)

где и - эмпирические и теоретические частоты соответственно.

С помощью величины по специальным таблицам приложения 3 определяется вероятность . Входами в таблицу являются значения и число степеней свободы. На основевыносится суждение о существенности или несущественности расхождения между эмпирическим и теоретическим распределением. Присчитается, что эмпирическое и теоретическое распределения близки, присовпадение между ними удовлетворительное, в остальных случаях - недостаточное.

Если число степеней свободы большое, то применяется соотношение, равное . Расхождение между эмпирическим и теоретическим распределениями существенно при значениях этой разности, заметно превосходящих 2.

Критерий Романовского (), также используемый для проверки близости эмпирического и теоретического распределений, определяется следующим образом:

.

(7.79)

где -критерий Пирсона, рассчитываемый по формуле (7.78);

- число степеней свободы (при проверке гипотезы о нормальности распределения равно числу групп минус три).

При различие несущественно, что позволяет считать эмпирическое распределение близким к нормальному.

Критерий Ястремского ()может быть найден на основе следующего соотношения:

.

(7.80)

где - объем совокупности;

- дисперсия альтернативного признака;

- число вариантов или групп;

- принимает значение 0,6 при числе вариантов или групп от 8 до 20.

Если , то эмпирическое распределение соответствует теоретическому.

Критерий Колмогорова ()вычисляется по формуле:

.

(7.81)

где - максимальное значение разности между накопленными эмпирическими и теоретическими частотами;

- сумма эмпирических частот.

Необходимым условием использования этого критерия является достаточно большое число наблюдений (не меньше ста).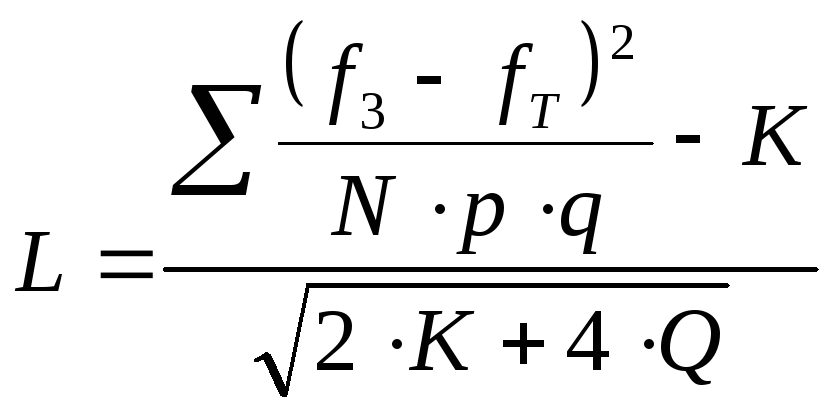