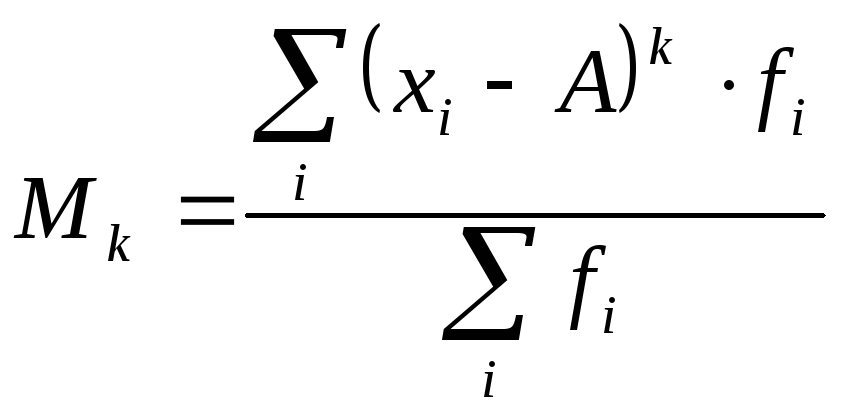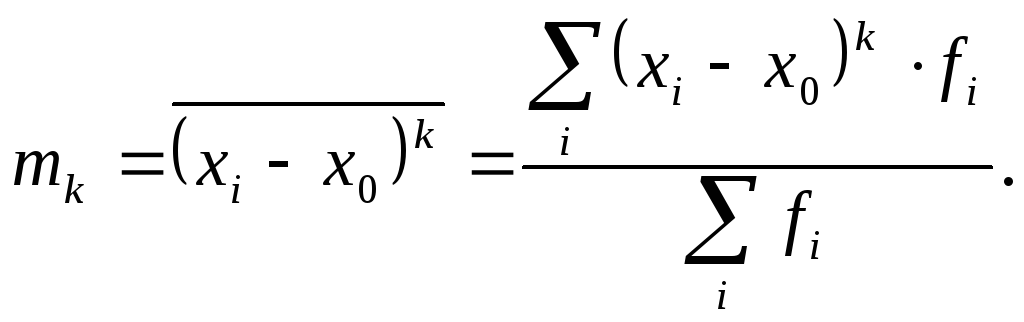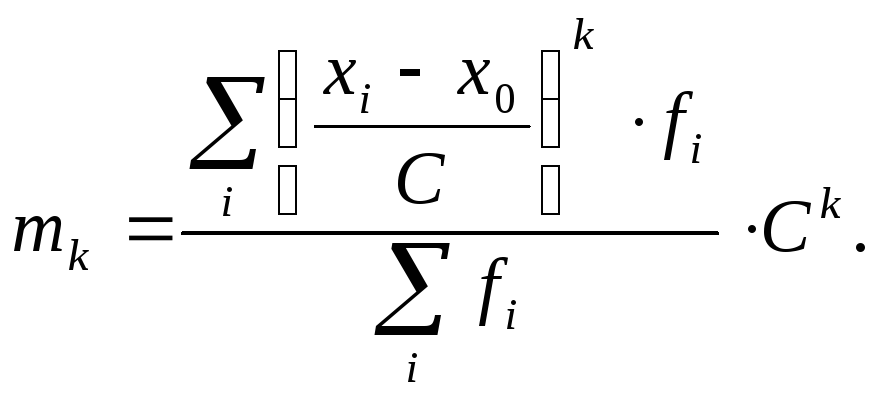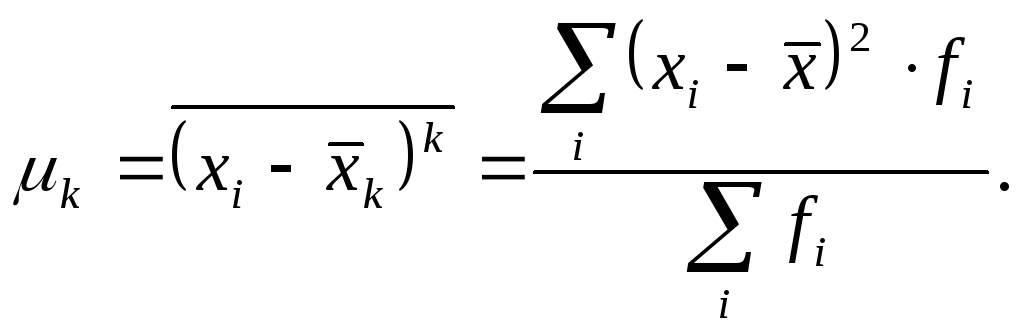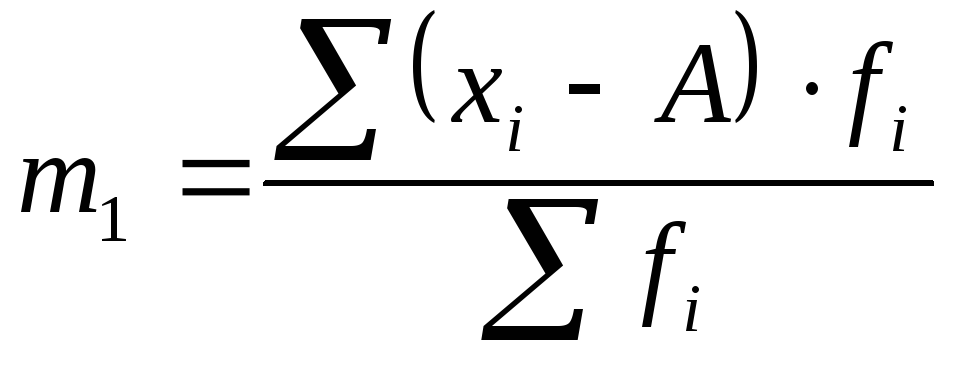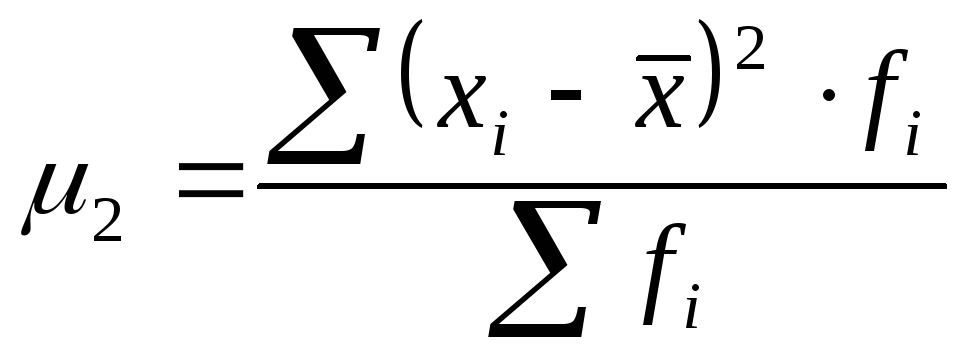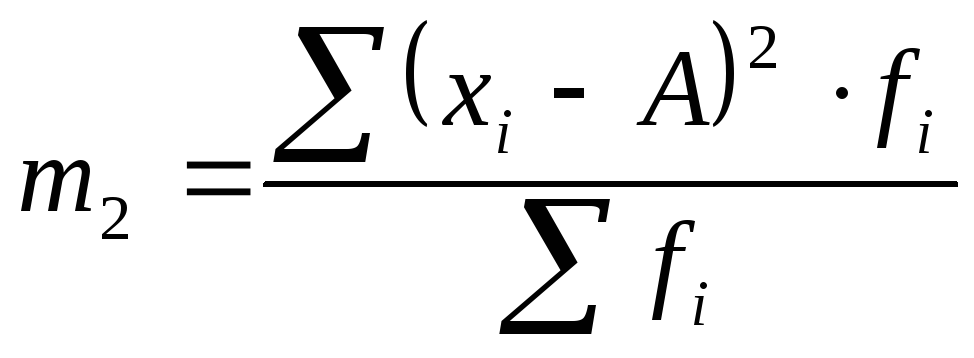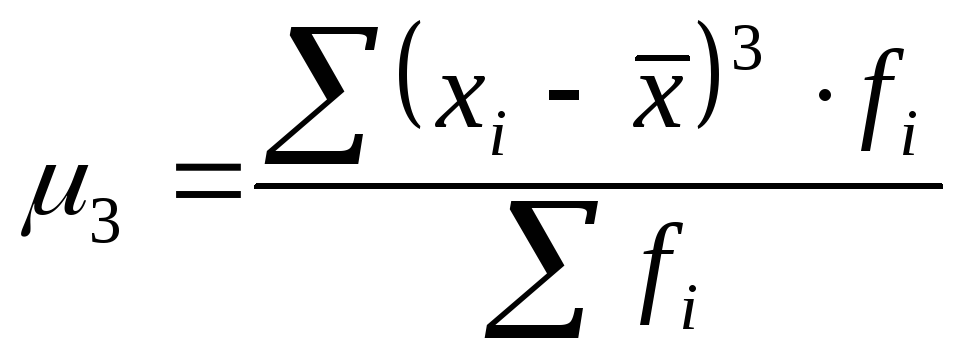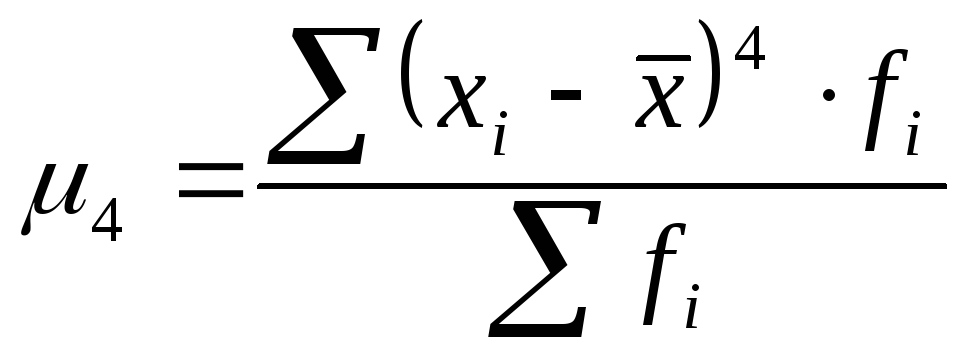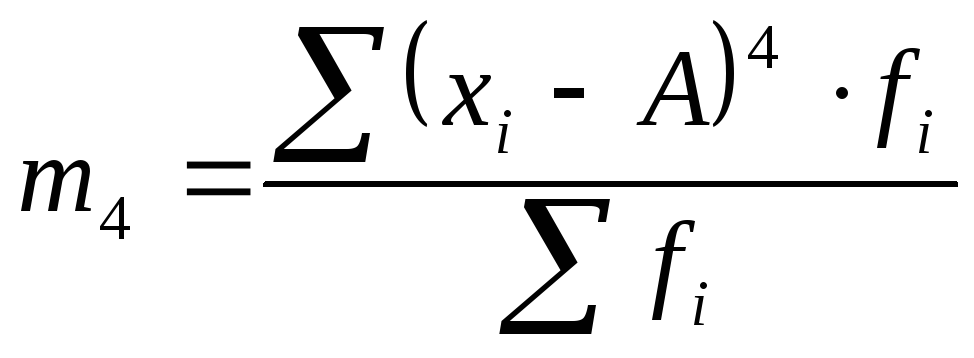7.7 Моменты распределения

Для подробного описания особенностей распределения используются дополнительные характеристики, в частности, определяются моменты распределения. Способ моментов был разработан русским математиком П.Л. Чебышевым и успешно применен А.А. Марковым для рассмотрения возможностей использования закона нормального распределения при изучении сумм большого, но конечного числа независимых случайных величин.

Моментом -го порядканазывается средняя из степеней отклонений вариантов от некоторой постоянной величины:

(7.61)

При исчислении средней в качестве весов могут быть использованы частоты, частости или вероятности. При использовании в качестве весов частот или частостей моменты называются эмпирическими, а при использовании вероятностей -теоретическими.

Порядок момента определяется величиной .Эмпирический момент -гопорядка определяется как отношение суммы произведений степеней отклонений вариантов от постоянной величины на частоты к сумме частот:

(7.62)

В зависимости от выбора постоянной величины различают три вида моментов:

1. Начальные моменты (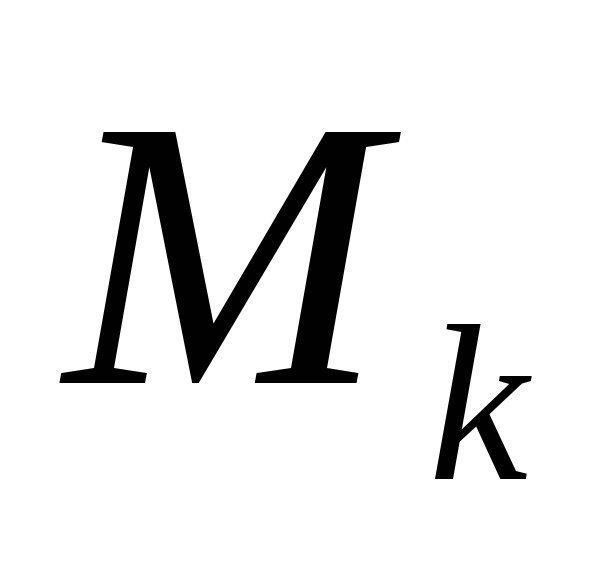) получаются, если постоянная величина равна нулю ():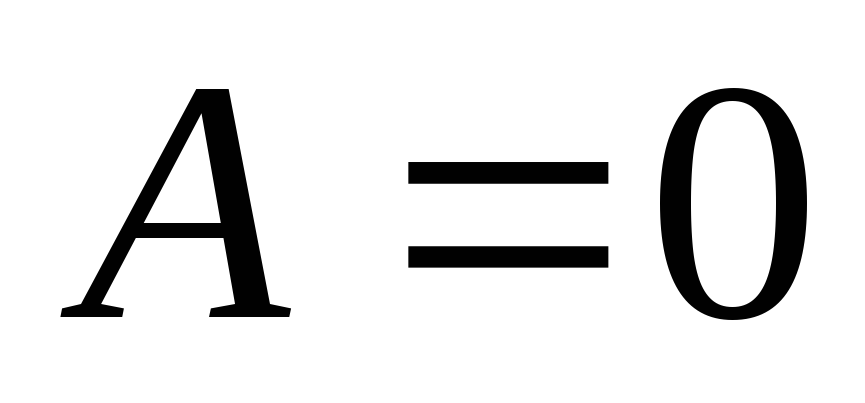

   (7.63)

2. Условные и начальные относительно 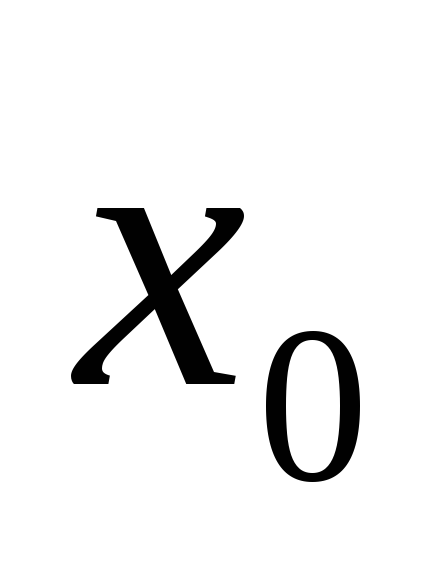моменты (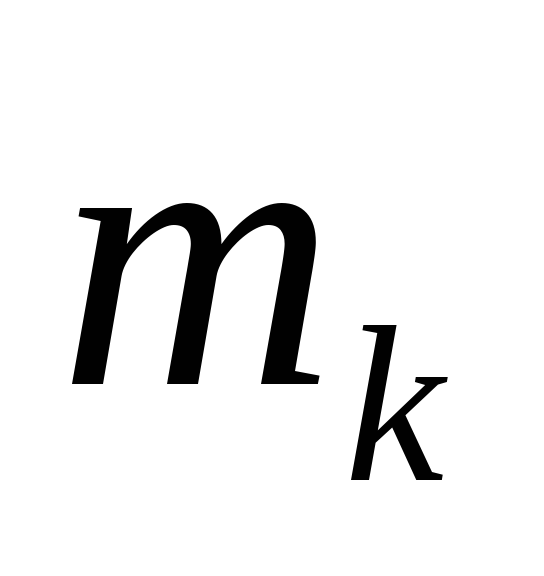)получаются при равном не нулю, а некоторой производной величине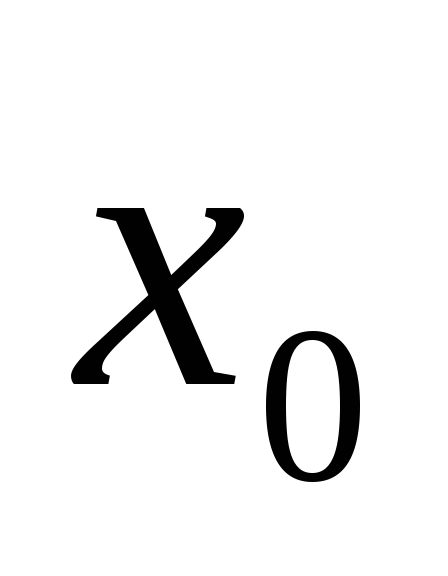 (начало отсчета):

(7.64)

С помощью условных моментов упрощается расчет основных характеристик ряда распределения. При подстановке различных значений получаем начальные моменты относительно. Так, например, если , то:

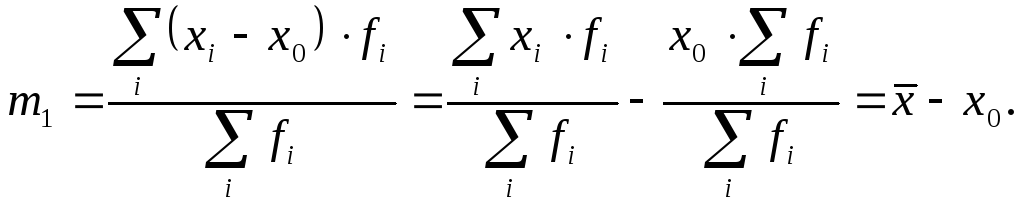
Из этой формулы вытекает, что , т.е. средняя арифметическая равна началу отсчета плюс начальный момент первого порядка. Если отклоненияимеют общий множитель, то на него можно разделить отклонения, а по окончании вычислить полученный момент, умножив на этот множитель в соответствующей степени, т.е.:

(7.65)

Отсюда следует, что при .

3. Центральные моменты (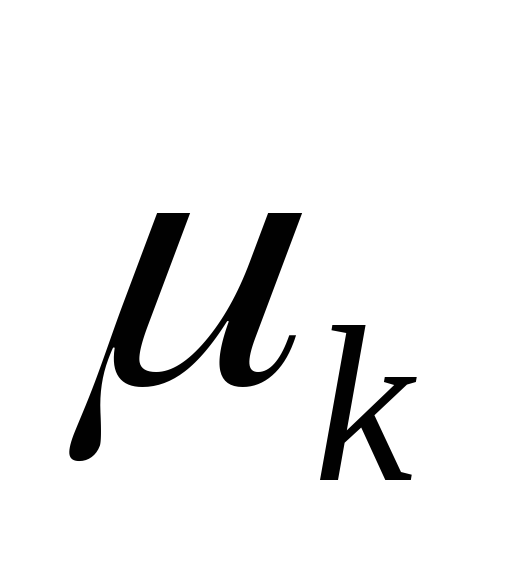) получаются, если за постоянную величину взять среднюю арифметическую ():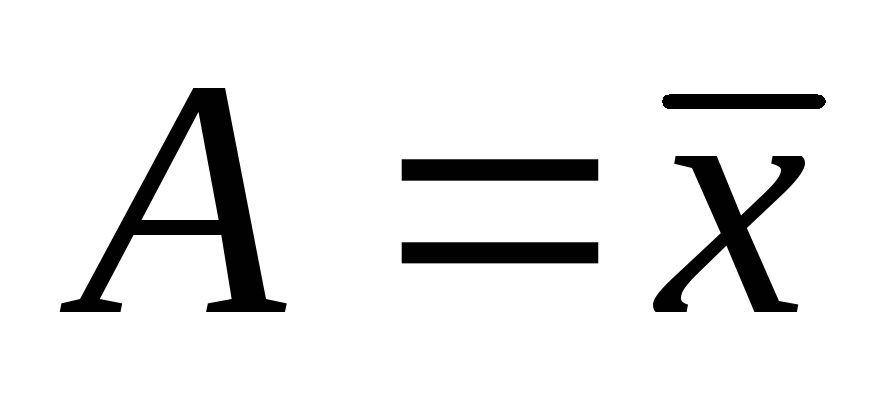

(7.66)

В статистической практике пользуются в основном моментами 1-го, 2-го, 3-го и 4-го порядков, которые представлены в табл. 7.1.

Таблица 7.1
Виды моментов распределения четырех порядков
Виды моментов Порядок	Начальные	Центральные	Условные
1-й
2-й
3-й
4-й

Таким образом, анализируя формулы моментов распределения в табл. 7.14, можно сделать следующие выводы:

• начальный момент первого порядка представляет собой среднюю арифметическую и используется как показатель центра распределения ();

• начальные моменты 2-го, 3-го и 4-го порядков не имеют самостоятельного значения, а используются для упрощения вычислений центральных моментов. Например, используя начальные моменты 1-го и 2-го порядка, можно получить дисперсию по такой формуле:

(7.67)

• центральный момент 1-го порядка всегда равен нулю в соответствии с нулевым свойством средней арифметической ();

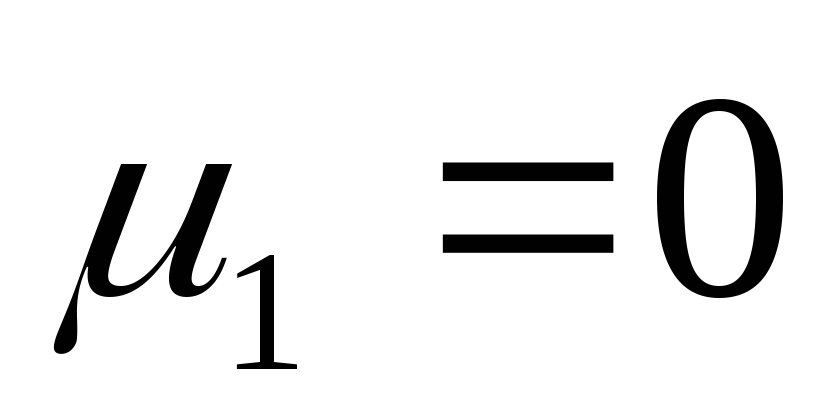• центральный момент 2-го порядка представляет собой дисперсию и служит основной мерой колеблемости признака ();

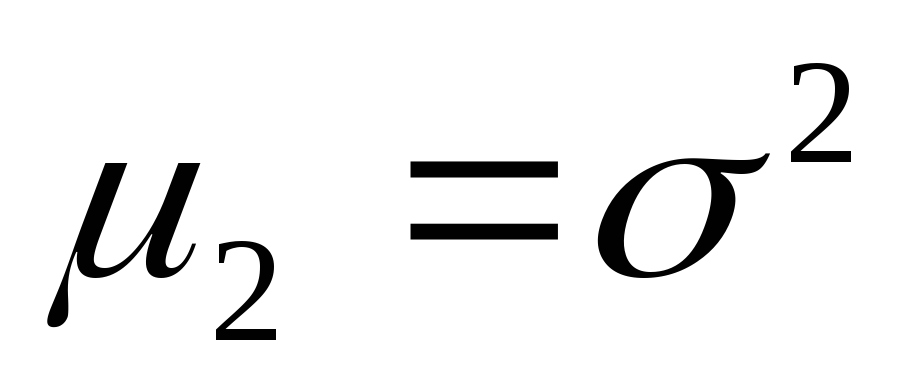• центральный момент 3-го порядка служит мерой асимметрии распределения, а если распределение симметрично, он равен нулю();

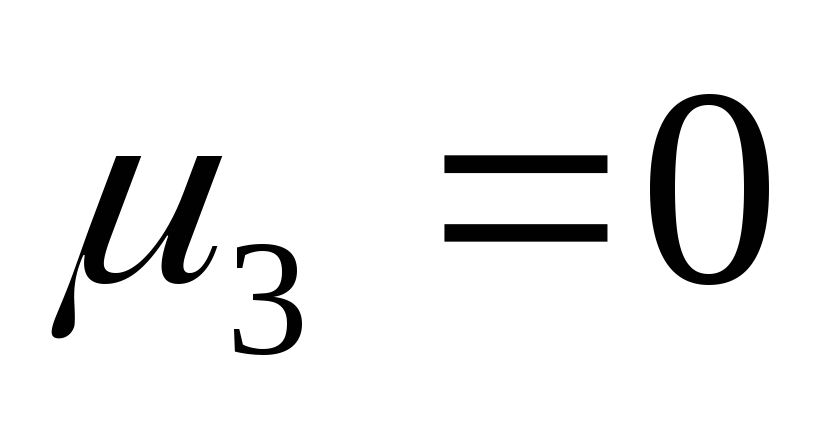• центральный момент четвертого порядка применяется при вычислении показателя эксцесса;

• условные моменты 1-го, 2-го, 3-го и 4-го порядков не имеют самостоятельного значения, а используются для упрощения вычислений центральных моментов.