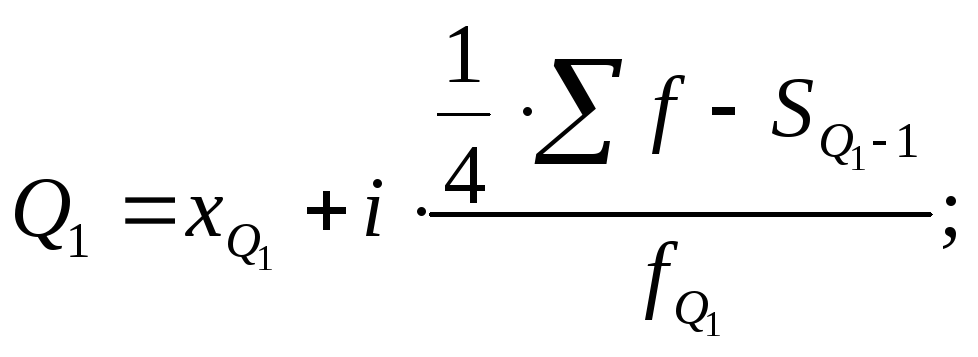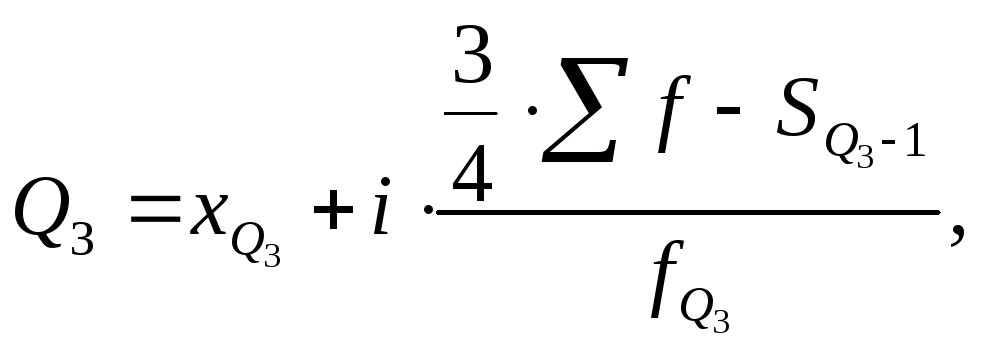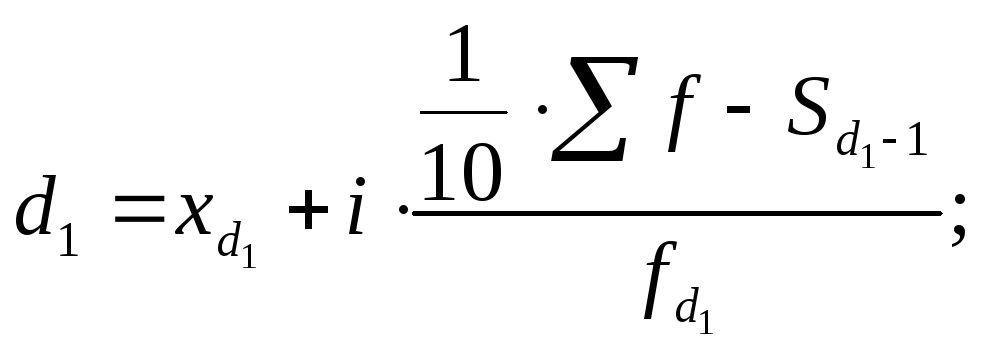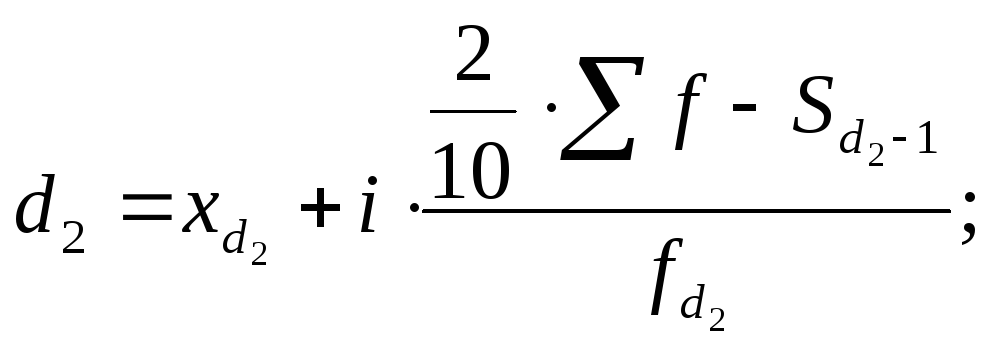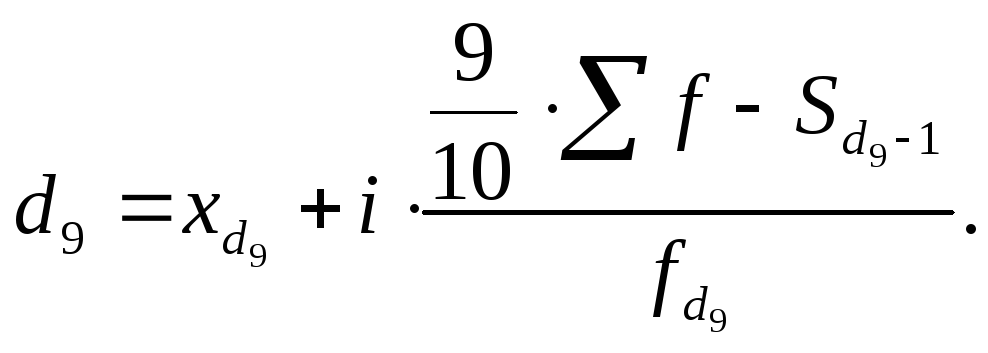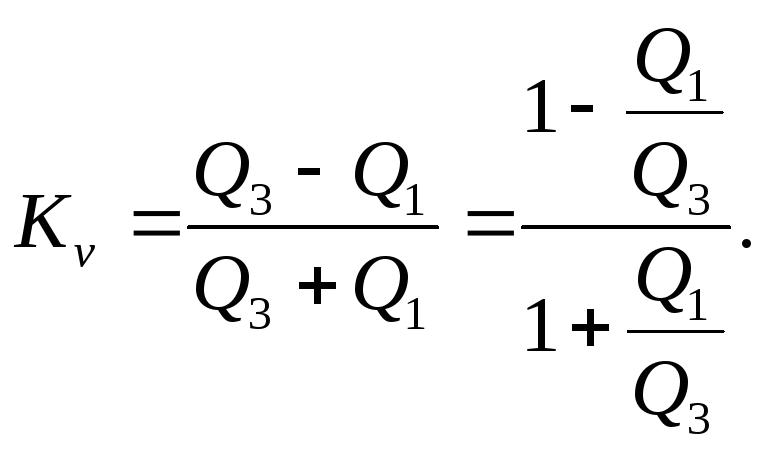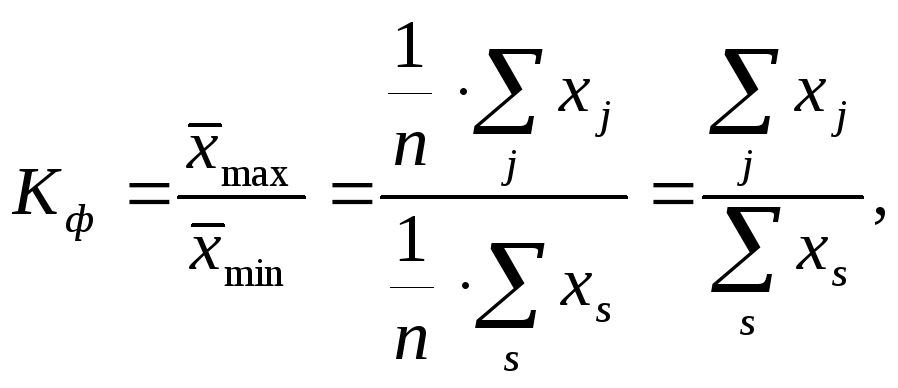7.6 Структурные характеристики вариационного ряда распределения. Показатели дифференциации

Рассмотренные обобщающие показатели центра распределения и степени вариации не дают понятия о форме распределения, т.е. не вскрывают характера последовательного изменения частот. Для выражения особенностей формы распределения применяются показатели дифференциации, основанные на структурных (ранговых) показателях распределения.

Структурные показатели. В системе структурных показателей в качестве показателей особенностей формы распределения выступают варианты, занимающие определенное место (каждое четвертое, пятое, десятое, двадцать пятое и т.д.) в ранжированном вариационном ряду. Такие показатели носят общее названиеквантилей, илиградиентов.

Некоторые квантили имеют особые наименования: квартили, квинтили, децили и перцентили.

Квартили представляют собой значение признака, делящее ранжированную совокупность на четыре равновеликие части. Различают квартиль нижний (), отделяющийчасть совокупности с наименьшими значениями признака, и квартиль верхний (), отсекающийчасть с наибольшими значениями признака. Это означает, что 25% единиц совокупности будут меньше по величине; 25% единиц будут заключены междуи; 25% - междуии остальные 25% превзойдут. Вторая квартиль является медианой. Вычисление квартилей аналогично вычислению медианы.

Для расчета квартилей по интервальному вариационному ряду используются формулы

	(7.51)
	(7.52)

где - нижняя граница интервала, содержащего нижний квартиль (интервал определяется по накопленной частоте, первой превышающей 25%);

- нижняя граница интервала, содержащего верхний квартиль (интервал определяется по накопленной частоте, первой превышающей 75%);

- величина интервала;

- накопленная частота интервала, предшествующего интервалу, содер­жащему нижний квартиль;

- то же для верхнего квартиля;

- частота интервала, содержащего нижний квартиль;

- то же для верхнего квартиля.

Квинтили делят распределение на пять равных частей.

Децили () - это значения вариант, которые делят ранжированный ряд на десять равных частей: 1-й дециль () делит совокупность в соотношениик,2-й дециль () - в соотношениики т.д.

Вычисляются децили по той же схеме, что и медиана, и квартили:

	(7.53)
	(7.54)

и т.д.

(7.55)

Значения признака, делящие ряд распределения на сто частей, называются перцентилями. Слово «перцентиль» относится непосредственно к элементу распределения или к значению, промежуточному между двумя элементами. Для того чтобы указать местоположение конкретного наблюдения, в распределении указывается так называемыйперцентильный ранг; он равен сумме процентов, приходящихся на наблюдения, которые в распределении стоят ниже его, и половине процентов, которые приходятся на него непосредственно.

Метод нахождения перцентилей можно представить с помощью следующей формулы:

(7.56)

где - обозначение-го перцентиля;

- нижняя граница интервала;

- число оценок, необходимое попасть в точку на горизонтальной оси, которая соответствует данному перцентилю;

- расстояние от нижней границы до верхней границы(шаг интервала);

- число оценок, расположенных в интервале от до.

Рассмотренные показатели можно представить в следующем со­отношении (рис. 7.3).

Использование в анализе вариационных рядов распределения рассмотренных выше характеристик позволяет глубоко и детально охарактеризовать изучаемую совокупность.

Показатели дифференциации. В тех случаях, когда при изучении вариационного ряда возникает необходимость дать относительную характеристику степени вариации ряда и имеются уже предварительно вычисленные квартили и децили, то можно вычислить коэффициент дифференциации ().

В зависимости от заданных ранговых показателей коэффициенты дифференциации рассчитываются по-разному.

1. Если заданы 3-я () и 1-я () квартили, то вместо коэффициента вариации () можно вычислитькоэффициент дифференциации по формуле

(7.57)

В большинстве случаев коэффициент вариации () составляет примерно 1,5 коэффициента дифференциации (), т.е.

(7.58)

1. Если сопоставляются 9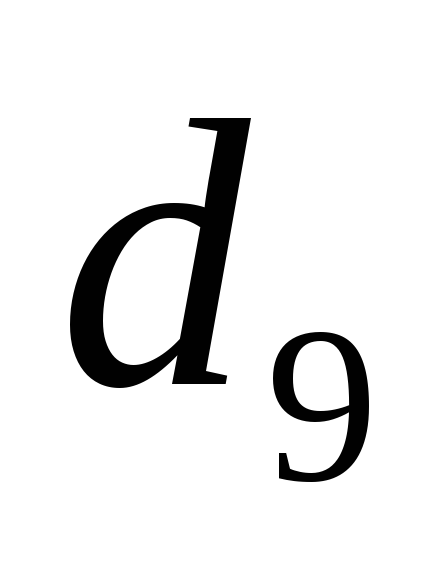-я () и 1-я () децили, тодецилъный коэффициент дифференциации (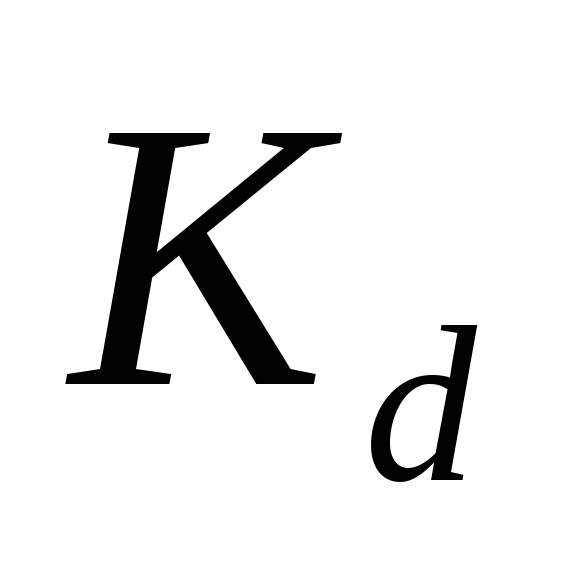) вычисляется по формуле:

(7.59)

Рассмотренный выше показатель дифференциации не совсем точно измеряет уровень дифференциации, так как сопоставляется минимальная величина признака (25% или 10% самых крупных единиц совокупности) с максимальной величиной признака (25% или 10% самых мелких единиц совокупности).

2. Более точно уровень дифференциации можно измерить, сопоставив средние уровни, полученные из 10% наибольших и наименьших значений признака в совокупности. Такой показатель называется коэффициентом фондовой дифференциации ().

(7.60)

где - сумма значений признака 10% самых крупных единиц в совокупности;

- число единиц совокупности самых крупных и мелких;

- сумма значений признака 10% самых мелких единиц в совокупности.