
- •Экзаменационные вопросы сухтп 1. Тау
- •1.01.Понятие типового динамического звена. Применение звеньев. Основные типы звеньев и их характеристики.
- •1.02. Использование преобразования Лапласа при рассмотрении систем автоматического регулирования (примеры).
- •1.03.Передаточные функции. Их получение и использование.
- •1.04. Частотная передаточная функция. Применение, примеры.
- •1.05.Передаточные функции типовых комбинаций звеньев.
- •1.06Изменение свойств динамического звена с помощью обратной связи (примеры).
- •Временные.
- •Частотные.
- •Временные.
- •Частотные.
- •1.11. Статические звенья второго порядка: уравнение, характеристики, основные свойства.
- •1. Идеальное дифференцирующее звено
- •2. Реальное дифференцирующее звено
- •1.16 Предельное усиление регулятора и обеспечение запаса устойчивости.
- •2. Способность к самовыравниванию.
Временные.
При подаче на вход статического звена нулевого порядка единичного ступенчатого воздействия оно передает входной сигнал мгновенно, без всяких искажений и запаздываний. Может наблюдаться изменение масштаба входного сигнала. Это изменение определяет величина статического коэффициента усиления.
Частотные.
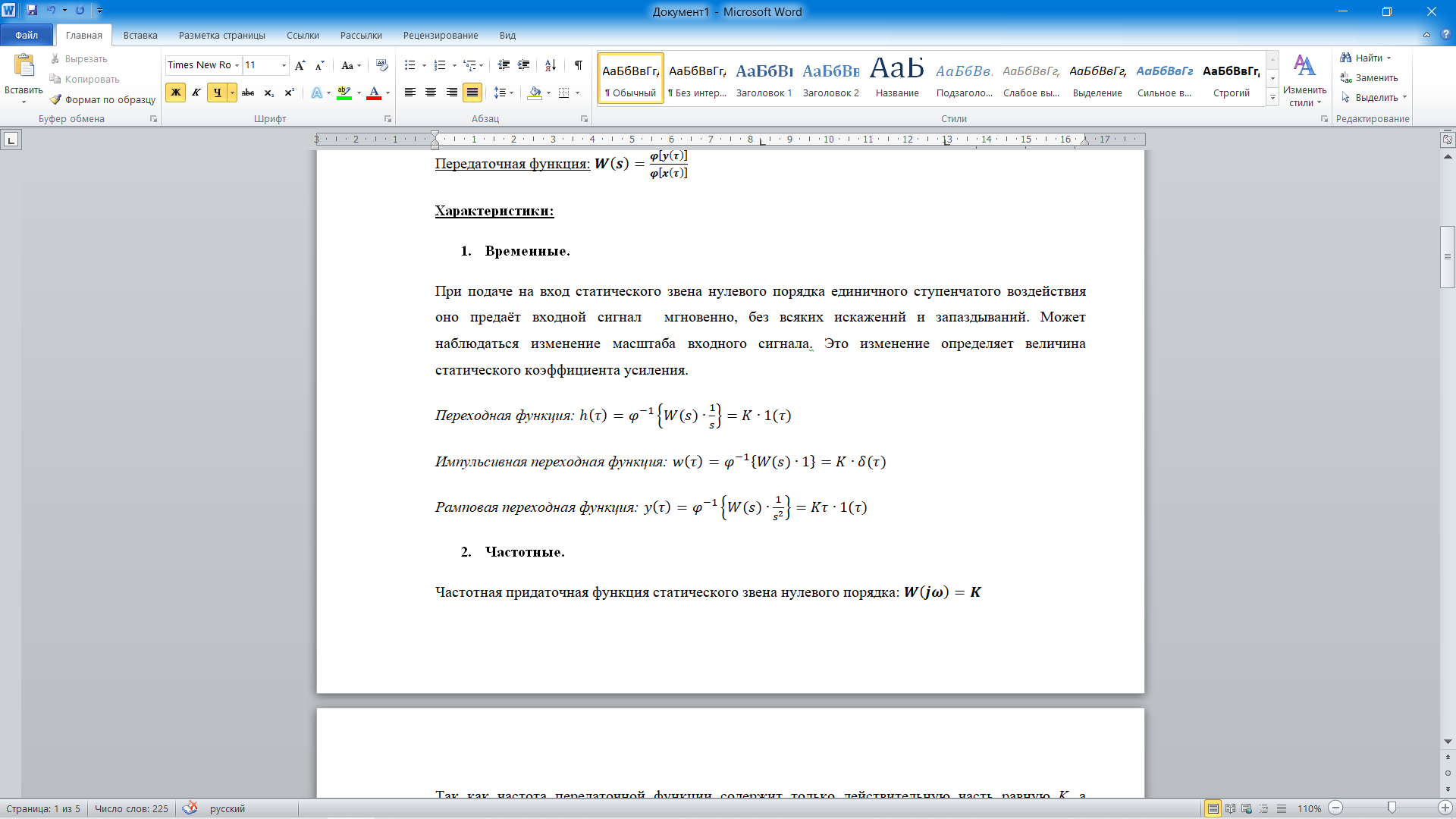
Частотная передаточная функция статического звена нулевого порядка: W(jω)=K
Так как частота передаточной функции содержит только действительную часть равную K, а мнимая часть равна 0, амплитудно-фазовая частотная характеристика (АФЧХ) статического звена нулевого порядка может быть изображена на комплексной плоскости одной точкой на действительной оси на расстоянии K от начала координат.


Статическое
звено первого порядка
– входная и выходная величины связаны
между собой дифференциальным уравнением:
![]()
T – постоянная времени статического звена первого порядка.
Примеры:

Характеристики:
Временные.
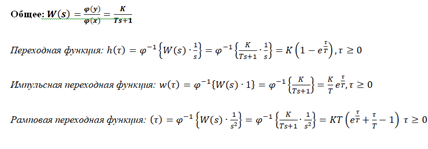

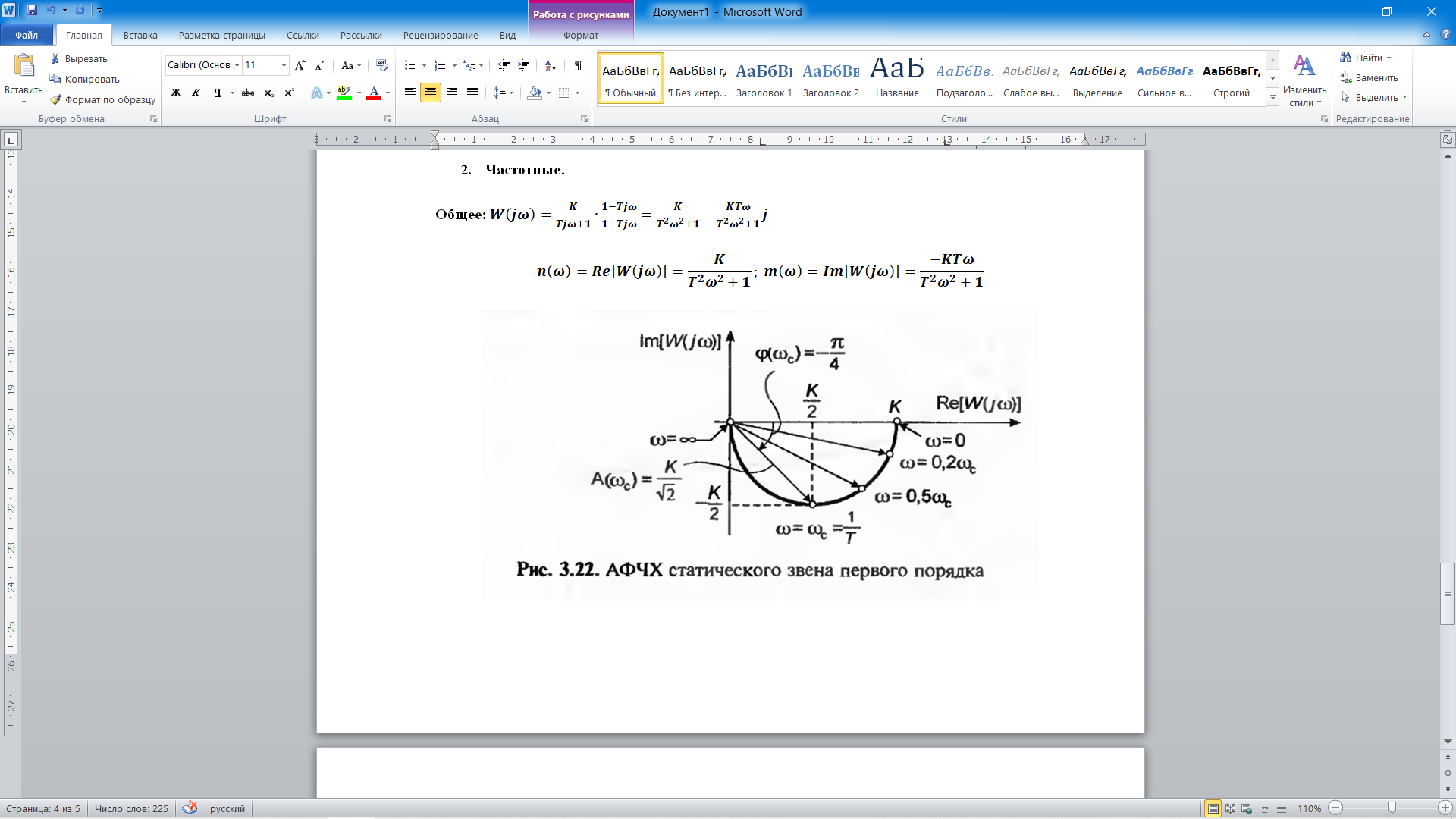
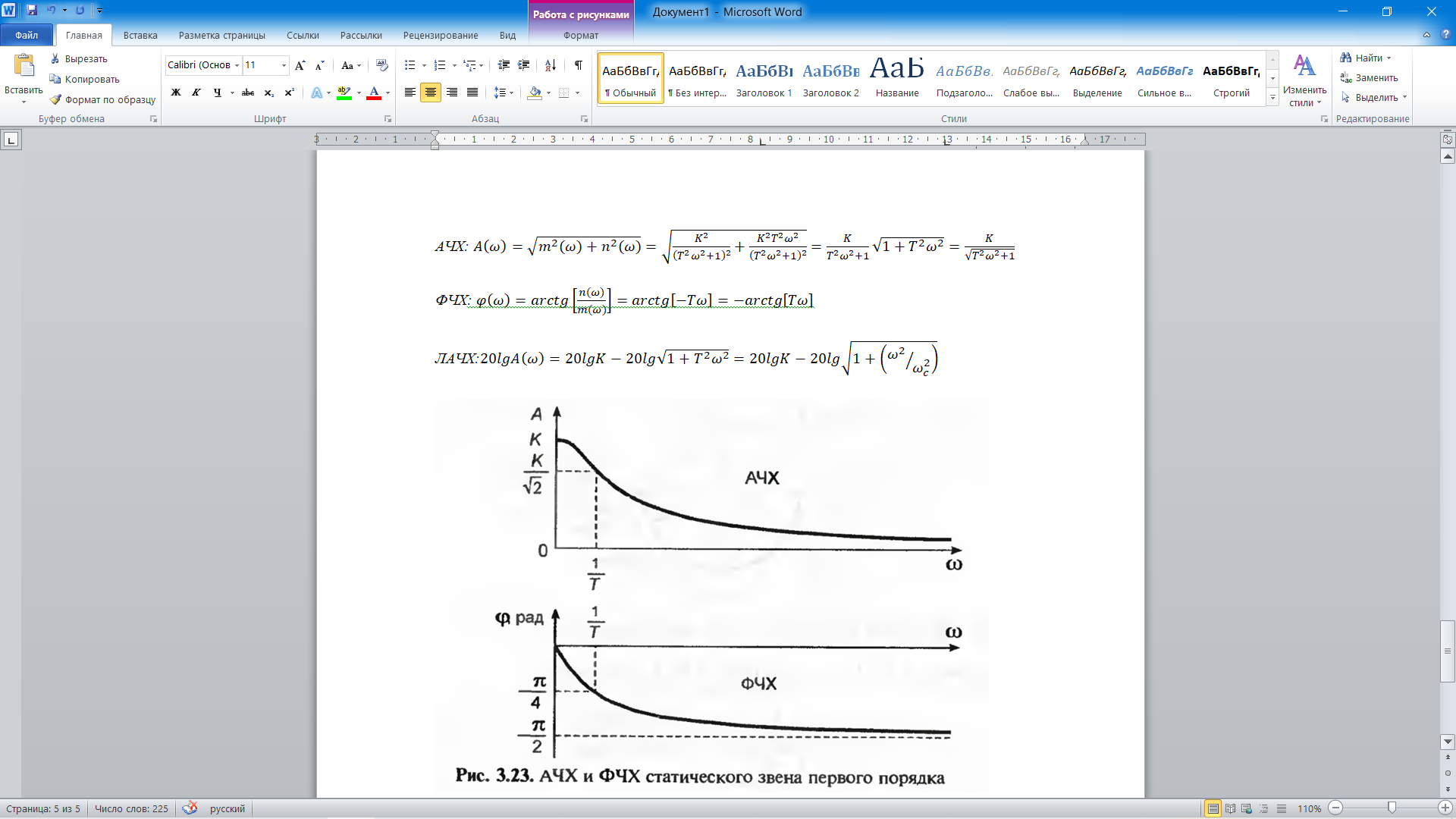
Частотные.

1.11. Статические звенья второго порядка: уравнение, характеристики, основные свойства.
Статическое звено второго порядка — Звено, входная и выходная величины которого связаны между собой линейным диф. уравнением второго порядка:
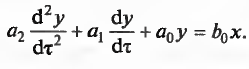
 -
само ур-е
-
само ур-е
1.12. (Фёдор Кривошеин)Идеальное интегрирующее звено: уравнение, характеристики, основные свойства.
1.13. Звено запаздывания: уравнение, характеристики, примеры.
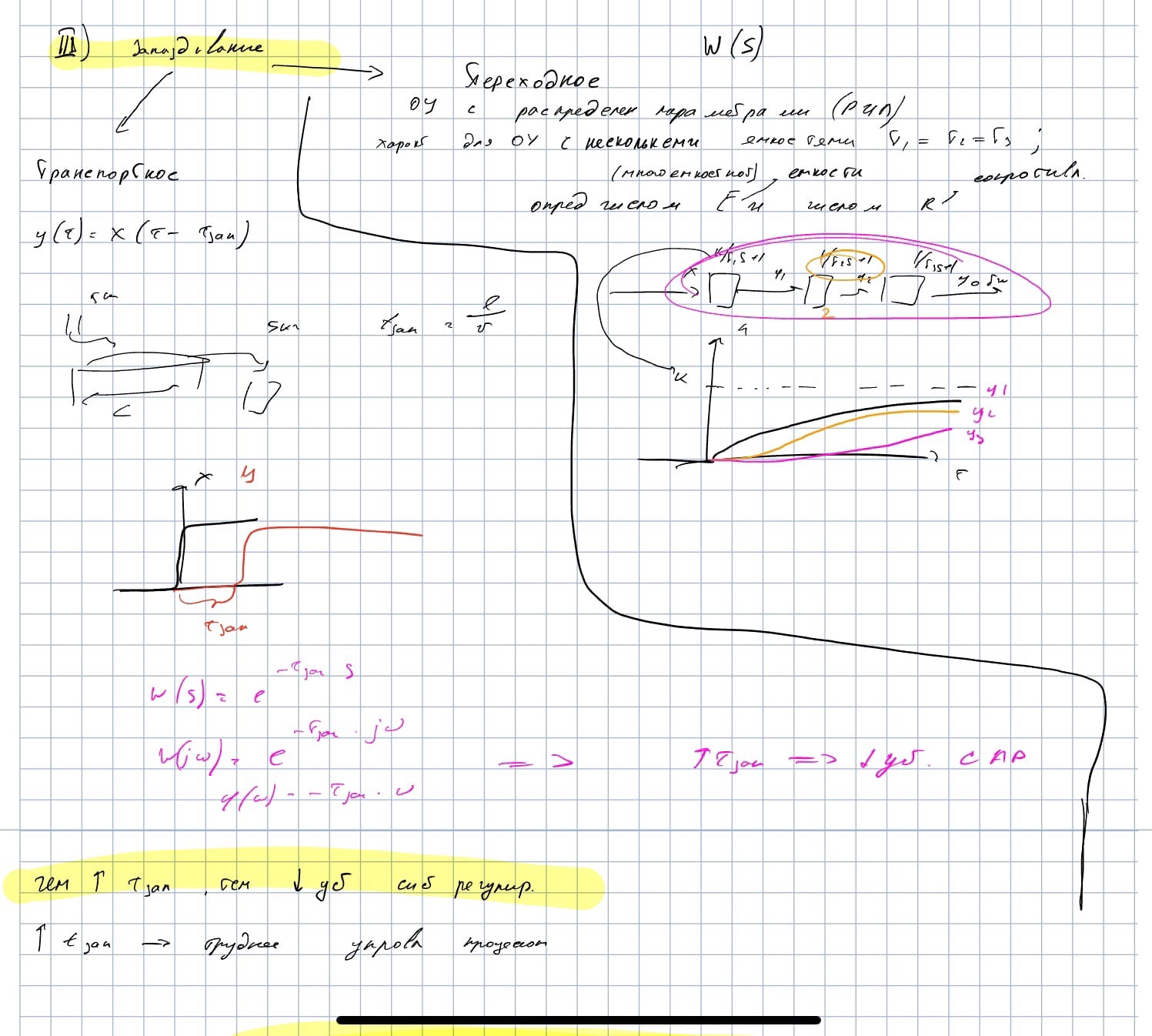
1.14. (Паша Гаврилюк)Дифференцирующие звенья: уравнение, характеристики, основные свойства.
1. Идеальное дифференцирующее звено



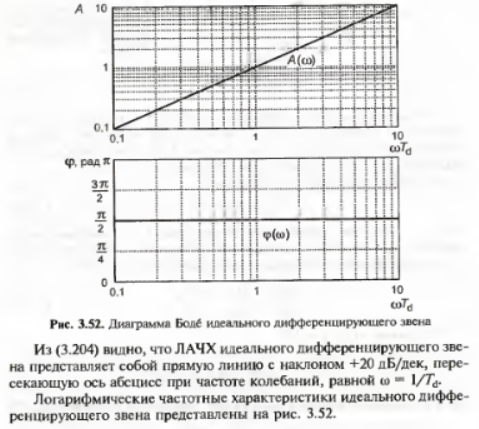
2. Реальное дифференцирующее звено




1.15.(Олеся Шевякова) Устойчивость систем автоматического регулирования.


1.16 Предельное усиление регулятора и обеспечение запаса устойчивости.
Стр 189 в учебнике






1.17. Определение устойчивости систем автоматического регулирования с помощью частотного критерия устойчивости Найквиста.
Частотный критерий Найквиста позволяет судить об устойчивости замкнутой линейной системы управления (объект и управляющее устройство соединены по принципу обратной отрицательной связи, рис. 3.66, а) по виду АФЧХ (амплитудно-фазовая частотная характеристика) системы в разомкнутом состоянии ( в этом случае объект и управляющее устройство соединены последовательно, рис. 3.66, б).

КЧХ(комплексная частотная характеристика) имеет действительное и мнимое слагаемые:

Формулировка самого критерия: замкнутая система управления устойчива, если она устойчива в разомкнутом состоянии и при этом АФЧХ разомкнутой системы не охватывает точку на комплексной плоскости с координатами (-1, j0). Если же АФЧХ устойчивой разомкнутой системы охватывает точку с координатами (-1, j0), то замкнутая система неустойчива.
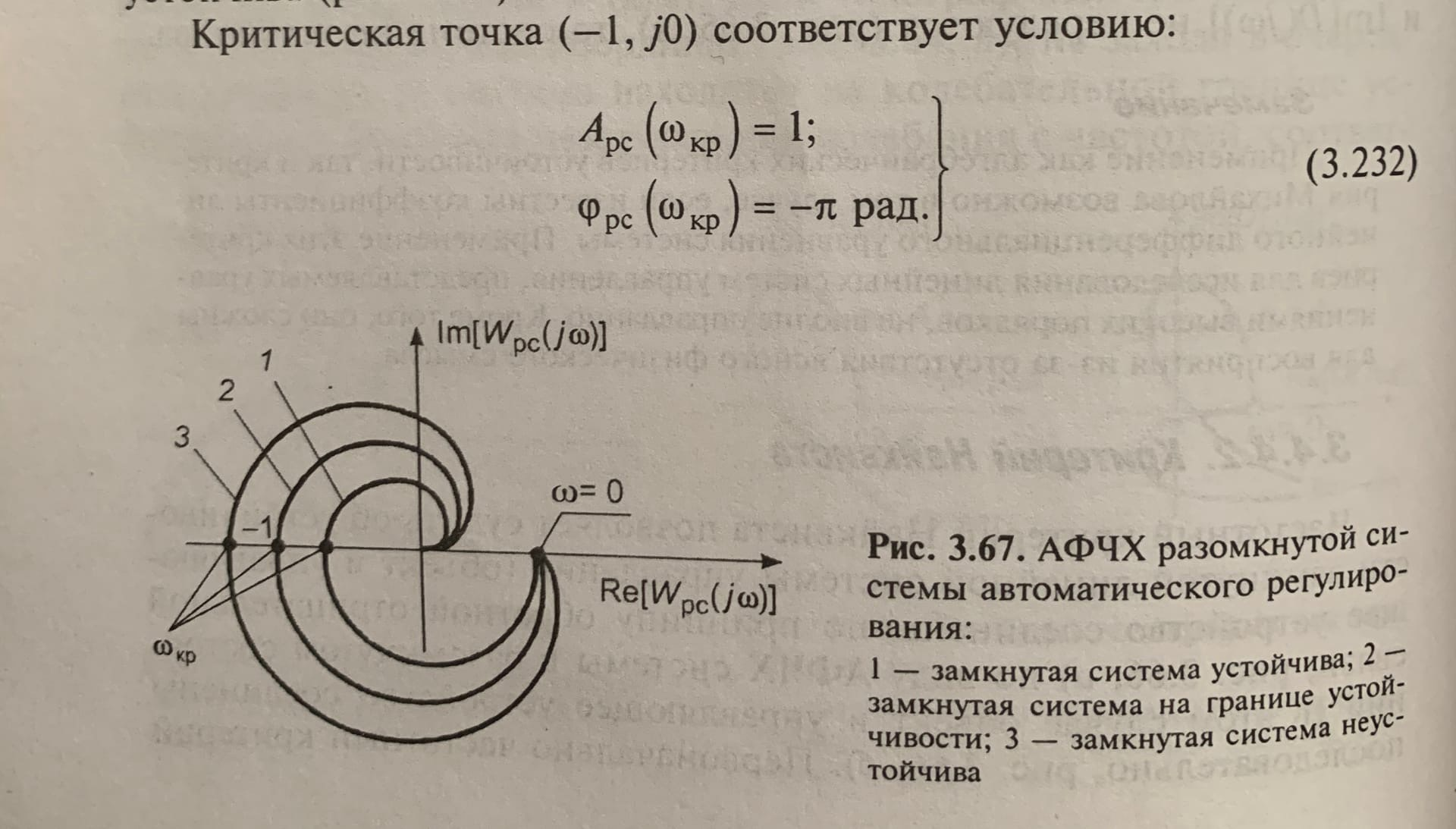

Частота, на которой фазовый сдвиг разомкнутой системы регулирования равен -пи (-180 град.), является резонансной частотой замкнутой системы регулирования.
1.18. Определение параметров настройки регулятора с помощью частотного критерия устойчивости Найквиста.
последнее фото предыдущего вопроса - нахождение предельного (максимального) усиления регулятора (Ар)
1.19. Статические, нейтральные и неустойчивые объекты регулирования.
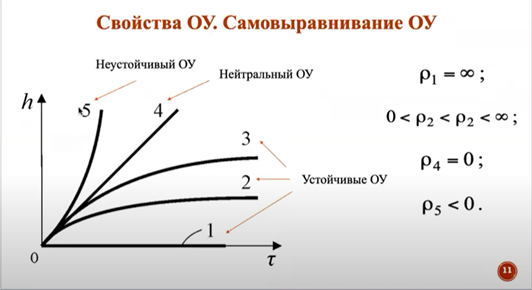
Если объект выходит на некое значение, то этот объект является устойчивым (статическим) объектом управления (1,2,3)
Если выходная величина у объекта изменяется с постоянной скоростью, то это нейтральный объект управления (4)
Если выходная величина изменяется с возрастающей скоростью, то это неустойчивый объект управления (5)
В случае устойчивого объекта управления степень самовыравнивания изменяется от 0 до ∞ (0 <p <∞)
Если степень самовыравнивания равна 0, то это нейтральный объект управления (p=0)
Если степень самовыравнивания меньше 0, то это неустойчивый объект управления (p <0)
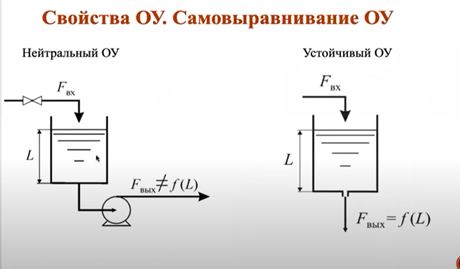
Нейтральный ОУ

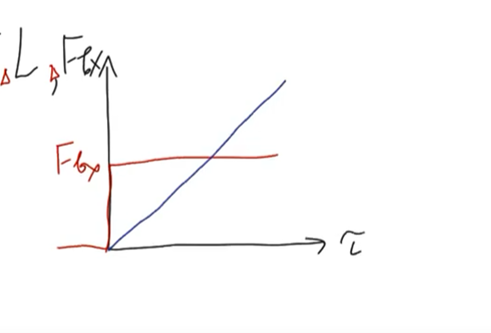
Устойчивый ОУ

1.20. (Вика Шилина)Самовыравнивание объектов регулирования: характеристики, примеры.
1.21. (Полина Митасова)Объекты регулирования с сосредоточенными параметрами и с распределёнными параметрами. Особенности регулирования объектов с распределёнными параметрами.
Выходные величины объектов с сосредоточенными параметрами не зависят от пространственной координаты и имеют в данный момент времени одно и то же числовое значение в каждой точке внутри объекта. Примерами таких объектов являются: химический реактор идеального смешения, резервуар со свободным истечением жидкости, газгольдер и т. д.
Объекты управления с сосредоточенными параметрами, свойства которых не изменяются во времени, называются стационарными и описываются обыкновенными дифференциальными уравнениями с постоянными коэффициентами. Дифференциальные уравнения дополняются начальными условиями.
Выходные величины объектов с распределенными параметрами в данный момент времени имеют разные числовые значения в различных точках объекта. Основные переменные процесса в объекте с распределенными параметрами изменяются и во времени, и в пространстве. Примерами объектов с распределенными параметрами являются трубчатые реакторы, массо-обменные колонные аппараты (ректификационные, дистилляционные, абсорбционные, экстракционные), кожухотрубные теплообменники, теплообменники «труба в трубе"

 1.22.
(Анастасия
Ведерникова)Выбор
закона действия регулятора и параметров
его настройки в зависимости от свойств
объекта регулирования.
1.22.
(Анастасия
Ведерникова)Выбор
закона действия регулятора и параметров
его настройки в зависимости от свойств
объекта регулирования.
 1.23.
(Егор
Муравский)Влияние
свойств объекта регулирования: на выбор
структуры системы регулирования; на
выбор закона действия регулятора; на
качество регулирования.
1.23.
(Егор
Муравский)Влияние
свойств объекта регулирования: на выбор
структуры системы регулирования; на
выбор закона действия регулятора; на
качество регулирования.
Свойства объектов регулирования: 1.Ёмкость - способность объекта накапливать или сохранять вещество или энергию.
Ёмкость влияет на качество регулирования следующим образом:
Ошибка регулирования.
а) Для систем регулирования с компенсацией возмущающего воздействия: чем больше ёмкость (С) объекта регулирования, тем меньше ошибка.
б) Для следящих и программных систем: чем больше ёмкость, тем больше ошибка.
Быстродействие.
Увеличение ёмкости объекта регулирования приводит к увеличению времени запаздывания, что уменьшает быстродействие системы.
