
- •Экзаменационные вопросы сухтп 1. Тау
- •1.01.Понятие типового динамического звена. Применение звеньев. Основные типы звеньев и их характеристики.
- •1.02. Использование преобразования Лапласа при рассмотрении систем автоматического регулирования (примеры).
- •1.03.Передаточные функции. Их получение и использование.
- •1.04. Частотная передаточная функция. Применение, примеры.
- •1.05.Передаточные функции типовых комбинаций звеньев.
- •1.06Изменение свойств динамического звена с помощью обратной связи (примеры).
- •Временные.
- •Частотные.
- •Временные.
- •Частотные.
- •1.11. Статические звенья второго порядка: уравнение, характеристики, основные свойства.
- •1. Идеальное дифференцирующее звено
- •2. Реальное дифференцирующее звено
- •1.16 Предельное усиление регулятора и обеспечение запаса устойчивости.
- •2. Способность к самовыравниванию.
1.04. Частотная передаточная функция. Применение, примеры.
Функция W (jw)
называется частотной передаточной
функцией или передаточной функцией
Фурье и равна отношению изображения
выходного сигнала к изображению входного
сигнала:

Частотная передаточная функция характеризует динамические свойства системы и не зависит от характера приложенных к системе воздействий. С ее помощью можно определить реакцию системы не только на гармонический входной сигнал, но и на любой другой входной сигнал, который может быть преобразован по Фурье.
Частотную передаточную функцию можно представить или в виде суммы действительной и мнимой частей:

Функции m(w) и n(w)
называются действительной (или
вещественной) и мнимой частотными
характеристиками звена, а функции А(w)
и φ(w) - амплитудной частотной и фазовой
частотной характеристиками. Взаимосвязь
между характеристиками определяется
следующими уравнениями:

![]()
Для каждого фиксированного значения частоты w=wi частотная передаточная функция может быть изображена на комплексной плоскости радиусом - вектором, длина которого равна А(wi), а угол поворота относительно положительного направления оси абсцисс равен фи.
1.05.Передаточные функции типовых комбинаций звеньев.
Последовательное соединение:

Параллельное соединение:

Соединение с обратной отрицательной связью:

Соединение с обратной положительной связью:
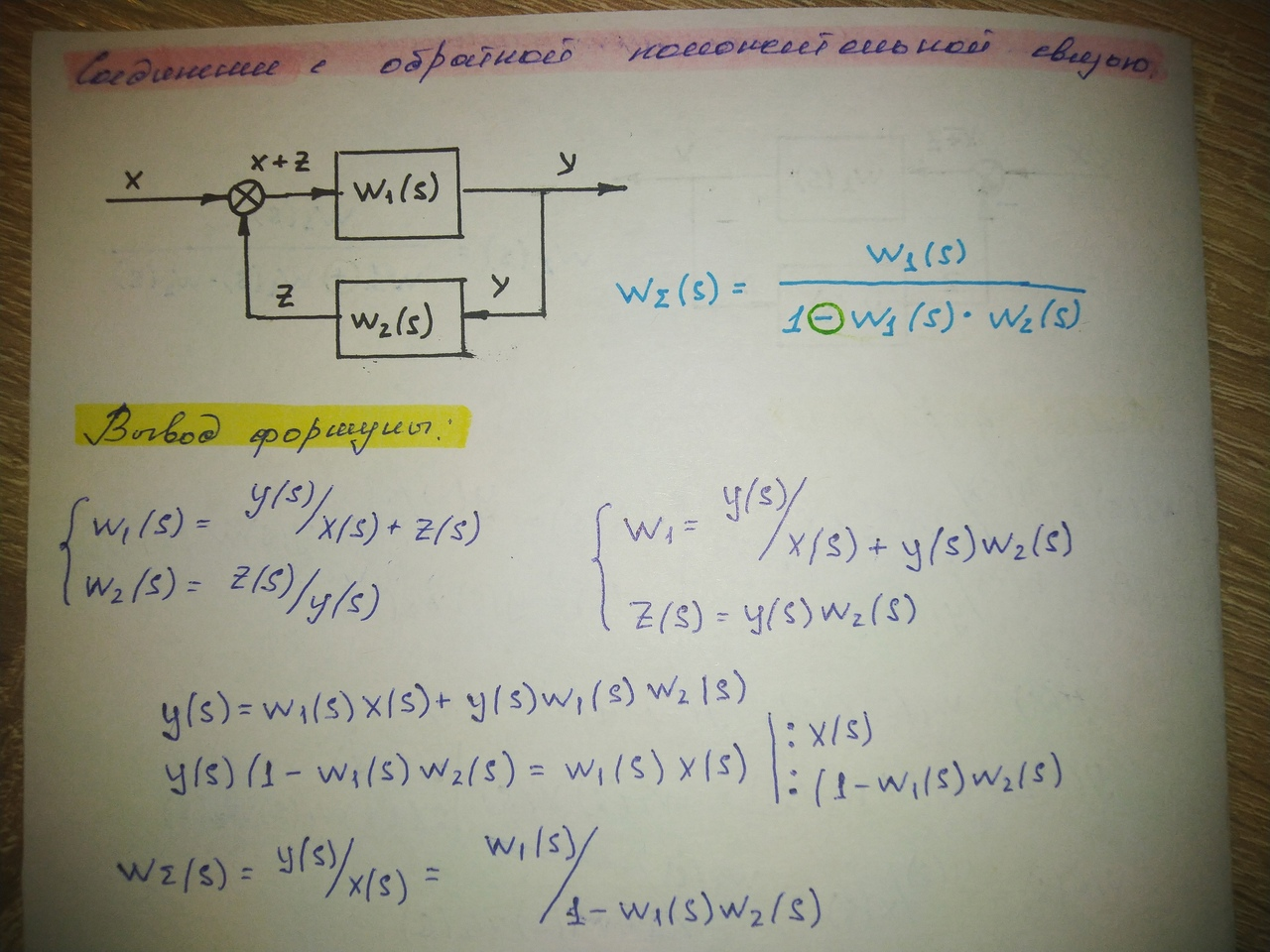
1.06Изменение свойств динамического звена с помощью обратной связи (примеры).
Обратная связь – связь, при которой на вход регулятора подается действительное значение выходной переменной, а также заданное значение регулируемой переменной.
– жесткая – такая ОС, при которой на вход регулятора поступает сигнал пропорциональный выходному сигналу объекта в любой момент времени.
– гибкая – такая ОС, при которой на вход регулятора поступает не только сигнал пропорциональный выходному сигналу объекта, но и сигнал пропорциональный производным выходной переменной.
Обратная связь может быть как положительной, так и отрицательной. Отрицательная обратная связь (ООС) действует в сторону уменьшения отклонений текущих значений координат объекта от их предшествующих значений, а положительная обратная связь (ПОС) действует в сторону увеличения. Следовательно, ООС позволяет строить наиболее точные САУ, так как несёт в себе информацию обо всех изменениях регулируемой величины; ПОС служит для изменения внутренних свойств отдельных звеньев САУ.
Пример 1. Рассмотрим, как меняются динамические свойства инерционного (апериодического) звена, охваченного жесткой ОС (рис. 7.6).




Из выражения (7.4) видно, что в результате охвата инерционного звена жесткой обратной связью его коэффициент усиления и постоянная времени изменятся в (l ± kkgc) раз, т. е. они уменьшатся в случае ООС и увеличатся при ПОС. По выражению (7.5) видно, что в результате коррекции мы получили снова инерционное звено.
Сравнивая переходные характеристики исходного звена h(t) и скорректированного h3(t) звена, охваченного ООС (рис. 7.7), можно отметить, что постоянная времени при использовании жесткой ООС станет меньше (переходный процесс форсируется), однако кэ тоже уменьшится, что приведет к ослаблению сигнала на выходе и снижению точности системы. Для компенсации снижения коэффициента усиления необходимо ввести дополнительный безынерционный усилитель с передаточной функцией


Отрицательная жесткая ОС широко применяется для повышения быстродействия инерционных исполнительных двигателей автоматических систем (электрических и гидравлических двигателей приводов).
Пример 2. Исследуем изменение динамических свойств инерционного звена при наличии гибкой обратной связи.



Из выражения (7.6) видно, что постоянная времени звена изменяется на величину ккдс, пропорциональную коэффициенту усиления звена ОС, причем ООС увеличивает постоянную времени, а положительная - уменьшает. При этом применение гибкой ПОС в отличие от жесткой ООС позволяет форсировать переходный процесс (повышать быстродействие) без снижения коэффициента усиления цепи. Переходные характеристики звена при отсутствии h(t) и при наличии h3(t) гибкой ПОС показаны на рис. 7.8, а.

Гибкая положительная обратная связь широко используется для повышения быстродействия инерционных усилителей (например, ЭМУ, гидравлических и пр.)
На рис. 7.8, б, показана переходная характеристика h3(t) при наличии гибкой ООС. В этом случае переходная характеристика при большом коэффициенте усиления звена обратной связи на ограниченном интервале времени близка к переходной характеристике интегрирующего звена. Следовательно, гибкая ООС, охватывающая инерционное звено, например, позволяет сформировать интегрирующее звено.
Таким образом, гибкая ПОС форсирует переходный процесс, а гибкая ООС, наоборот, ослабляет, замедляет переходный процесс.
Пример 3. Рассмотрим случай, когда безынерционный усилитель с большим коэффициентом передачи к охвачен отрицательной обратной связью.

Из выражения (7.7) видно, что с помощью мощного безынерционного усилителя можно получить звено с передаточной функцией, обратной передаточной функции звена ОС.

Таким образом, с помощью дифференцирующего звена в цепи ОС получаем интегрирующее звено. Такой способ, в частности, широко применяется в аналоговых вычислительных машинах.
Рассмотренные примеры показывают, что обратные связи являются эффективным средством получения требуемых динамических характеристик звеньев и систем в целом.
1.07. Получение временных характеристик объекта экспериментально и из его дифференциального уравнения, их использование.
Временной
характеристикой звена называют закон
изменения выходной величины звена во
времени у(тау) в ответ на изменение
входного воздействия х(тау) при условии,
что до приложения входного воздействия
звено находилось в покое.


1.08. Частотные характеристики звеньев.
Частотные характеристики звеньев
АФЧХ W(j)=A(w)
A(w) - АЧХ
φ(W ) – ФИХ
Ф-ия W(j) называется частотной передаточной функцией, или передаточной функцией Фурье, или [комплексной] частотной характеристикой, и равна по определению отношению изображ. Фурье выходного сигнала динамического звена к изображ. Фурье входного сигнала:

Характеризует динамич. Свойства системы и не зависит от характера приложенных к системе воздействий. С ее помощью опред. Р-ию. Системы на входной сигнал.
W(jw)=Re[w(jw)] + j*lm[W(jw)] = m(w)+j*n(w)
Re[w(jw)] – действ. часть j*lm[W(jw)] – мнимая часть
W(jw)= |W(jw)|e^(j*argW(jw)) = A(w)*e^(jφ(w))
A(w)*e^(jφ(w)) – амплитуда частотной и фаз. хар-ки.

1.09. Исследование систем управления с помощью частотных характеристик.

Отличительная особенность частотных методов - робастность (грубость). Созданная с помощью частотных методов система управления сохраняет требуемые характеристики, несмотря на небольшие различия между реальной системой управления и теоретической моделью.
Частотные характеристики можно получить на основе математической модели САУ и экспериментально. Экспериментальный метод применяют, когда невозможно получить мат описание системы из-за сложности или малой изученности системы.
С помощью частотных характеристик можно:
проверить адекватность мат модели системы, построив ее частотные характеристики и сравнив их с экспериментальными частотными характеристиками реальной системы
получить характеристику системы в целом по характеристикам отдельных элементов системы независимо от их числа
определить тип регулятора, критическую частоту, предельно допустимое усиление регулятора, запас устойчивости и полосу пропускания системы управления
исследовать временные характеристики
Определяя в установившемся режиме отношение амплитуд колебаний выходной величины и входного сигнала и фазовый сдвиг между колебаниями выходной величины и входного сигнала при разных частотах колебания входного сигнала, можно экспериментально получить частотные характеристики звена.
1.10. Статические звенья нулевого и первого порядка, их характеристики, примеры.
Статическое звено нулевого порядка – это входная и выходная величина связана между собой зависимостью y(τ)=Kx(τ).
Выходная величина статического звена нулевого порядка пропорциональна входной величине не только в статическом, но и в динамическом режиме в каждый момент времени.
Примеры: рычаг, механические передаточные механизмы (зубчатая передача), редукторы, усилители различных физических величин (электронный усилитель), регулирующие клапаны с линеаризованными расходными характеристиками (изменение расхода жидкости пропорционально изменению положения штока регулирующего клапана).

Передаточная функция: W(s)=φ[y(τ)]/φ[x(τ)]
Характеристики:
