Экзаменационные вопросы сухтп 1. Тау
1.01.Понятие типового динамического звена. Применение звеньев. Основные типы звеньев и их характеристики.
Динамическое звено — это математическая модель системы управления или любого ее элемента, отражающая определенные динамические свойства элемента вне зависимости от физической природы протекающих в нем процессов. Например, с точки зрения динамических свойств устройства являются одинаковыми динамическими звеньями, если описываются одним и тем же дифференциальным уравнениями.
Динамические звенья называют типовыми, если изменение проходящего через них сигнала можно описать алгебраическим или дифференциальным уравнением не выше второго порядка (как правило, линейным неоднородным дифференциальным уравнением с постоянными коэффициентами), например:
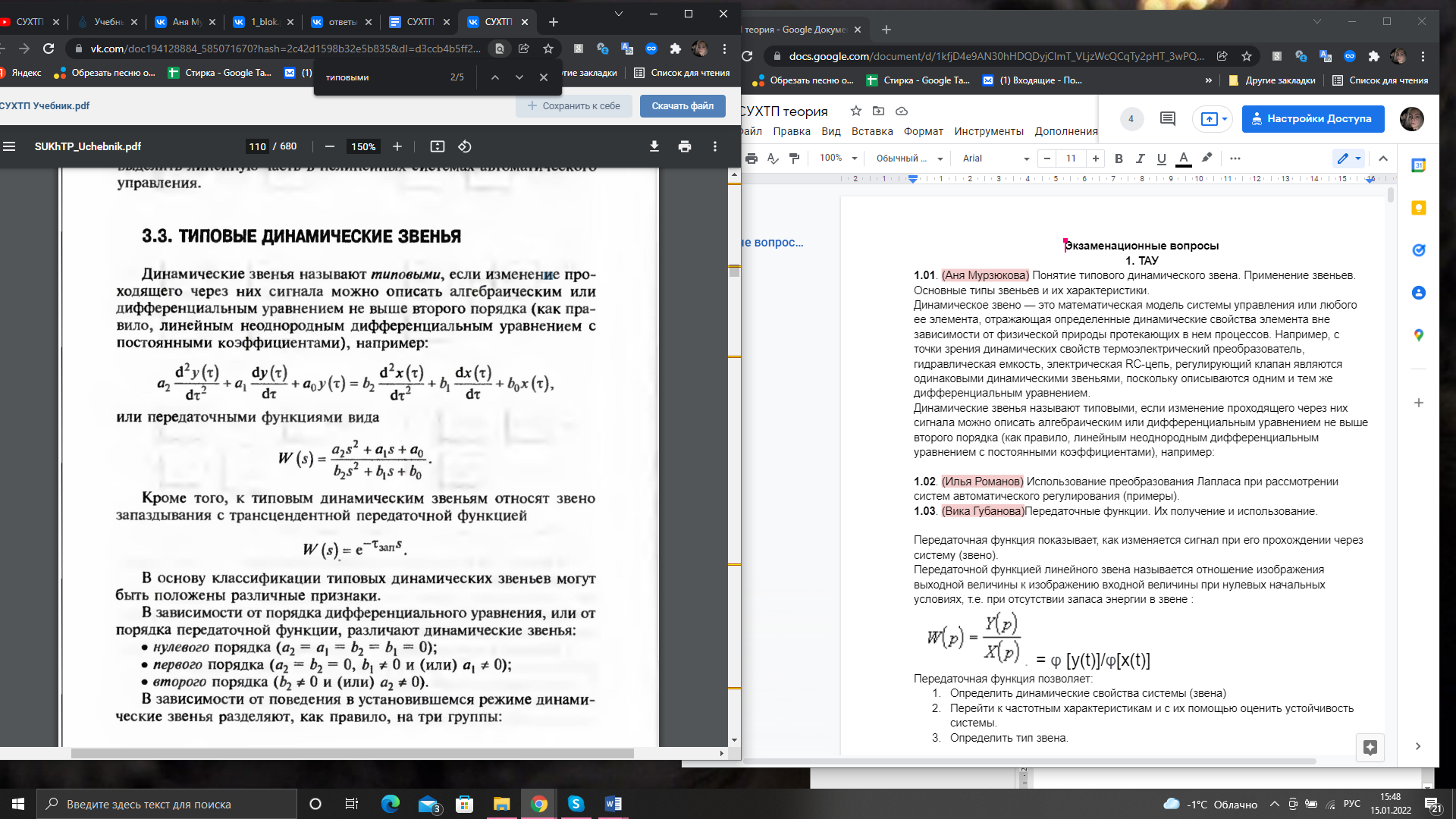
В основу классификации типовых динамических звеньев могут быть положены различные признаки. В зависимости от порядка дифференциального уравнения, или от порядка передаточной функции, различают динамические звенья:
• нулевого порядка (а2 = а1= b2 = b1 = 0);
• первого порядка (а2 = b2 = 0, b1 ≠ 0 и (или) a1 ≠ 0);
• второго порядка (b2 ≠ 0 и (или) а2 ≠ 0).
В зависимости от поведения в установившемся режиме динамические звенья разделяют, как правило, на три группы:
• звенья статические, или позиционные (b0 ≠ 0 и а0 ≠ 0), входной и выходной сигналы которых в статическом режиме связаны между собой взаимно однозначной функцией
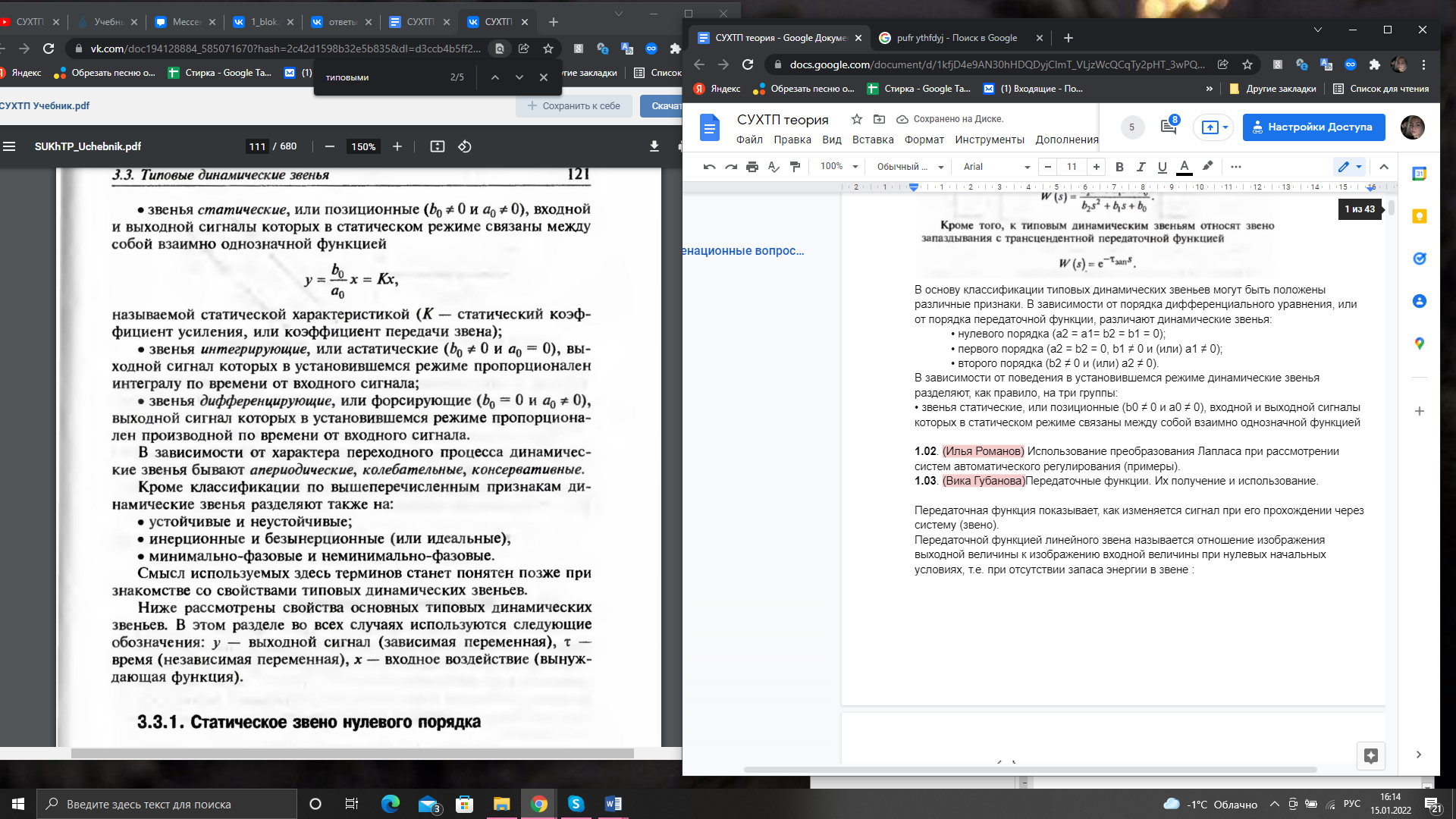называемой
статической характеристикой (К —
статический коэффициент усиления, или
коэффициент передачи звена);
• звенья интегрирующие, или астатические (b0 ≠ 0 и а0 = 0), выходной сигнал которых в установившемся режиме пропорционален интегралу по времени от входного сигнала;
• звенья дифференцирующие, или форсирующие (b0 = 0 и а0 ≠ 0), выходной сигнал которых в установившемся режиме пропорционален производной по времени от входного сигнала.
В зависимости от характера переходного процесса динамические звенья бывают апериодические, колебательные, консервативные.
Кроме классификации по вышеперечисленным признакам динамические звенья разделяют также на: • устойчивые и неустойчивые; • инерционные и безынерционные (или идеальные), • минимально-фазовые и неминимально-фазовые.
1.02. Использование преобразования Лапласа при рассмотрении систем автоматического регулирования (примеры).
Преобразование Лапласа — математический метод, позволяющий сравнительно просто решать линейные дифференциальные уравнения.
Преобразование Лапласа имеет достаточно полные таблицы преобразования, позволяют ввести понятие передаточная функция и получить частотные характеристики САУ, что делает их распространенными при решении уравнений переходного процесса в САУ.
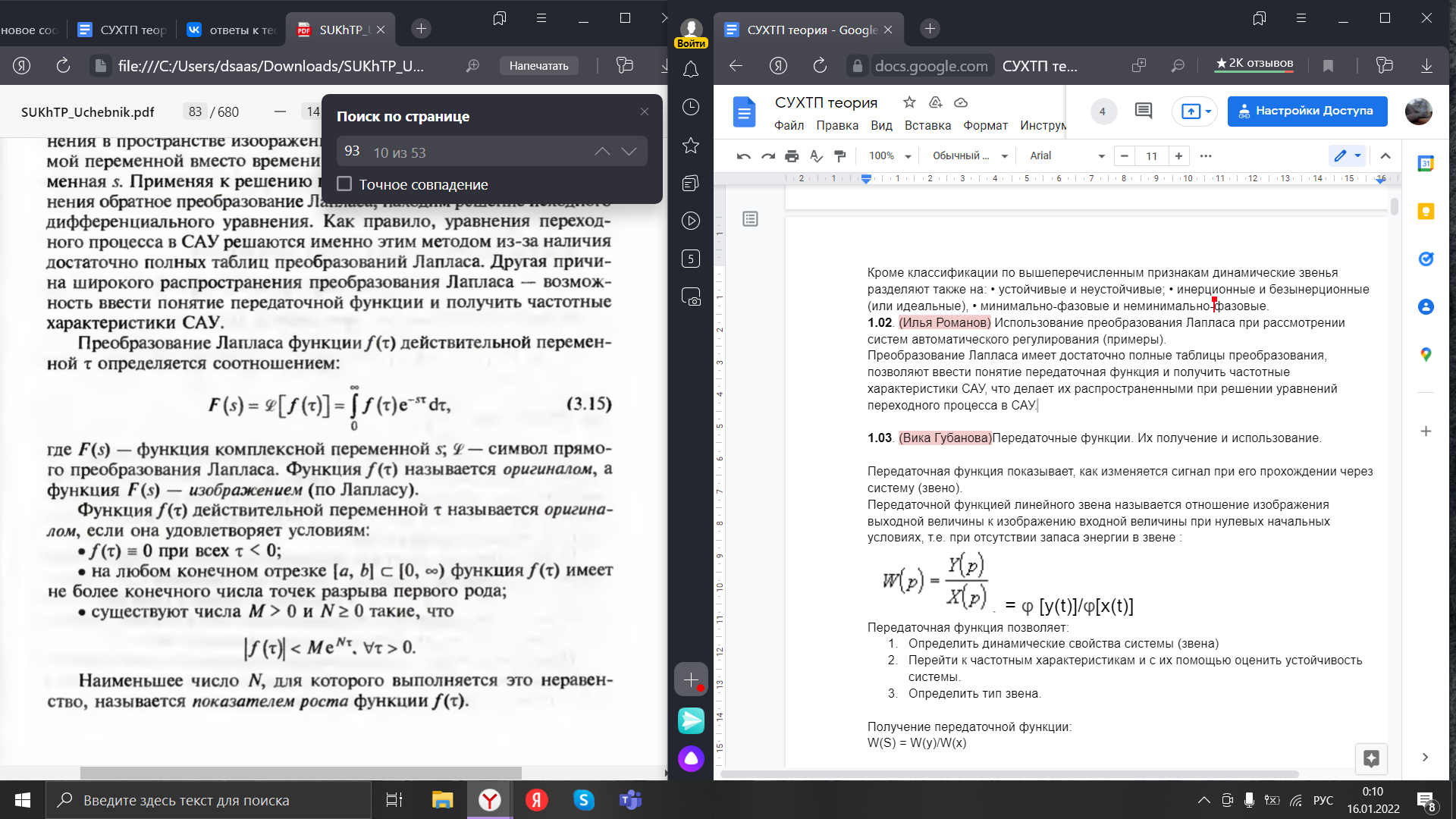
где F(s) - функция комплексной переменной s
Фи - символ прямого преобразования Лапласа f(t) - функция оригинала
F(s) - изображение по Лапласу
Пример:
1.03.Передаточные функции. Их получение и использование.
Передаточная функция показывает, как изменяется сигнал при его прохождении через систему (звено).
Передаточной функцией линейного звена называется отношение изображения выходной величины к изображению входной величины при нулевых начальных условиях, т.е. при отсутствии запаса энергии в звене :
=
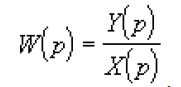φ
[y(t)]/φ[x(t)]
Передаточная функция позволяет:
Определить динамические свойства системы (звена)
Перейти к частотным характеристикам и с их помощью оценить устойчивость системы.
Определить тип звена.
Получение передаточной функции:
W(S) = W(y)/W(x)
или же
Дано Dy 1-го порядка
Преобразование уравнения по Лапласу - необходимо заменить x(t) и y(t) на x(p) и y(p), а вместо знака производной записать оператор p: Tpy(p) + y(p) = x(p)
Вынесем y(p) за скобки и найдём отношение y(p)/x(p), которое является передаточной функцией W(p) = y(p)/x(p) = k/Tp+1
Статическое звено 2-го порядка
На структурной схеме каждое типовое динамическое звено показывается прямоугольником, в котором записывается передаточная функция звена.
Общая передаточная функция при последовательном соединении звеньев равна их произведению.