Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Балтийский федеральный университет им. И.Канта

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

matan_3_sem

.pdf

Скачиваний:

317

Добавлен:

10.02.2015

Размер:

17.04 Mб

Скачать

☆

<<< < Предыдущая 1 2 34 / 84 5 6 7 8 > Следующая >>>

406

n0 : x [a;b] и

n n0

Sn x S x

b a

Обозначим:

S x

Un t dt

S t dt

n 1

Sn x Uk t dt Uk t dt Sn t dt

Оценим разность:

k 1 x0

x0 k 1

n x

Un t dt Uk t dt

S x Sn x

S t dt Sn t dt

x0 n 1

k 1 x0

S t Sn t

x x0

b a

Для x [a;b] и

n n0

, следовательно, ряд Un t dt

сходится на отрезке

n 1 x0

[a;b] равномерно к функции

Un t dt , т.е. справедливо равенство (1).

Пример:

n 1

Исследовать на сходимость ряд

arctg

Рассмотрим ряд:

n 1

...

1 x

4 x

9 x

n 1 n

Для любого действительного числа

, а ряд

- сходящийся, следова-

n 1

тельно, по признаку Вейерштрасса ряд

- сходится равномерно на всей

числовой оси.

n 1 n

Проинтегрируем его на отрезке [0;x]

arctg

0 n 1 n

n 1 0 n

n 1 n

По теореме о почленном интегрировании функциональных рядов он сходится равномерно на всей числовой оси.

Теорема ( о почленном дифференцировании функционального ряда)

Если функциональный ряд Un x с непрерывно дифференцируемыми на отрезке

n 1

[a;b] членами сходится к функции S(x), а ряд Un x – сходится равномерно на

n 1

этом отрезке, то исходный ряд Un x - сходится равномерно на[a;b] , его сумма

n 1

S(x) – непрерывно дифференцируемая функция и справедливо равенство

407



Un x
n 1

Доказательство:


S x Un x	(2)

n 1

Обозначим через x Un x .

n 1

Проинтегрируем это равенство на x0,x a,b

x		x				x
x dt Un x dt Un x dt
x0		x0 n 1			n 1 x0

Un t	xx0	Un x Un x0 S x S x0


n 1		n 1
(Левая часть полученного равенства дифференцируема по x , следовательно, и
			x
			x

правая часть дифференцируема по x)				t dt	S x S x0 тогда
правая часть дифференцируема по x)				t dt	S x S x0 тогда		S (t) t , сле-
			x0

довательно, справедливо равенство (2).

Равномерная сходимость ряда Un x следует из предыдущей теоремы.

n 1

Пример:

Найти сумму ряда:

nxn 1

1 2x 3x2

... nxn 1

n 1

Ряд xn сходится при

S(x)

n 1

1 x

nxn 1

сходится при

nxn 1

nqn 1 ,

q 1 т.е. сходится равномерно по признаку

n 1

n 1 qn

Вейерштрасса, D lim

q 1

– сходится,

nqn 1

n 1

dx n 1

1 x

Определение: Ряд вида:

§4 Степенные ряды

a0 a1 x a2 x 2

... an x n ... an x n,

(1)

n 0

где an, - действительные числа – называется степенным рядом по степе-

ням x , an - коэффициенты степенного ряда.

При α=0, получаем ряд


a0 a1x a2x2 ... anxn ... an xn.	(2)

n 0

В дальнейшем будем рассматривать ряды вида (2) т.к. ряды вида (1) приводится к виду (2) заменой переменной x- =t.

Для степенных рядов справедлива

Теорема (теорема Абеля).

408

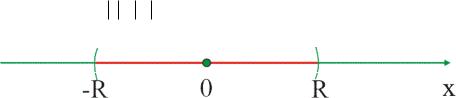
Если степенной ряд an xn. сходится в точке x0 0, то он сходится абсолютно в

n 0

интервале

и сходится равномерно на отрезке -q x q, 0 q

Доказательство :

1) Т.к. по условию теоремы числовой ряд an xn. - сходится, тогда lim anx0n 0,

n 0

всякая сходящаяся последовательность – ограничена, следовательно,

M 0 :

M, n N .

Пусть

, тогда рассмотрим

anxn

anx0n

n 0

Члены ряда M

- образуют геометрическую прогрессию со знаменателем

n 0

. Что бы этот ряд сходился необходимо и достаточно

1 ,

, т.е. ряд

(2) сходится абсолютно при

2). Если

, то

1. Ряд (2) мажорируется сходящимся числовым

q n

рядом

, следовательно, по признаку Вейерштрасса он сходится равномер-

n 0

но на отрезке [-q;q].

Следствие :

Если в точке x0 0, степенной ряд an xn. расходится, то он расходится во всех

n 0

точках х, таких что x x0

Из теоремы Абеля и следствия вытекает, что если степенной ряд anxn ,

n 0

сходящийся хотя бы в одной точке x0 0, то всегда существует число R>0 и сте-

пенной ряд сходится абсолютно для всех x (-R;R) и расходится во всех x ;R R; .

При x= R ряд может, как сходится, так и расходится. Неотрицательное число R называется радиусом сходимости ряда. Интервал

(-R;R)называется интервалом сходимости. (радиус сходимости R– половина интервала сходимости).

Для нахождения радиуса сходимости степенного ряда используют признаки Даламбера и Коши и формулы для радиуса сходимости, получающиеся из этих признаков.

409

1. anxn

n 0

Пусть lim n

L, тогда

lim n

an xn

, при

1 – ряд сходится абсолютно;

при L

1 - расходится, следовательно

;

lim

(3)

n n

2.Аналогично из признака Даламбера

an 1

lim

an 1xn 1

то

. Тогда

Пусть lim

, тогда

. Если d

lim

an 1

R lim

(4)

an 1

Пример1 :

n!xn

Найти радиус сходимости ряда n 1

2n 1!!

Имеем a

n 1!

n! n 1

. Найдем предел

2n 1!!

2n 1!! 2n 1

2n 1!!

n 1

lim

n! 2n 1!! 2n 1

lim

2n 1

R lim

an 1

n 1

n n! 2n 1!! n 1

Пример 2 Найти область сходимости ряда

n!x

(a>1)

n 1 a

lim

an e

lim n

Следовательно, ряд сходится на всей числовой оси.

Теорема.

§5. Свойства степенных рядов.

Если радиус сходимости степенного ряда

anxn отличен от 0, то его сумма

n 0

S(x) непрерывна на интервале сходимости(-R;R).

Доказательство.

Пусть x – произвольная точка интервала сходимости. Всегда существует та-

кое число q>0, что |x|<q<R.

По теореме Абеля степенной ряд сходится равномерно на отрезке [-q;q] (-

R;R).

410

Тогда, согласно теореме (о непрерывности суммы равномерно сходящегося функционального ряда), S(x) непрерывна на отрезке [-q;q], а, следовательно, и в точке x.

В силу произвольности выбора точки x (-R;R) получаем непрерывность функции на (-R;R).

Теорема.

Операция почленного дифференцирования и интегрирования на любом про-

межутке x0;x R;R степенного ряда
	anxn не изменяет радиуса сходимости.
Доказательство.	n 0

Ограничимся рассмотрением случая, когда R lim an

n an 1

Обозначим R1 – радиус сходимости почленно продифференцированного ряда.

(an xn ) nan xn 1

					n 0	n 1
Тогда			nan		an	R.
	R1	lim	nan	lim	an

			(n 1)an 1
		n	(n 1)an 1	n an 1

Аналогично:

Пусть R2 – радиус сходимости ряда, полученного почленным интегрированием:

tn 1

xn 1

x0n 1

ant

= an

n 1

n 0

n 1

n 0

n 1

Числовой ряд an

сходится абсолютно по признаку сравнения, в силу нера-

n 1

венства

n 1

n 0

anx0

an x0

n 1

nan x0n -сходится, т.к.

(-R;R).

n 1

an (n 2)

an )

R .

lim

(n 1)an 1

n an 1

Теорема.

Если радиус сходимости степенного ряда an xn отличен от 0, то сте-

n 0

пенной ряд можно почленно дифференцировать на интервале сходимости, и для его суммы S(x) справедливо равенство:

		n 1	;	(1)
	x
S (x) nan

n 1

Доказательство.

Пусть x – произвольная точка интервала сходимости (-R;R).Выберем такое число q, что |x|<q<R.

На отрезке [-q;q] (-R;R) степенной ряд сходится равномерно(теорема Абе-

ля).

411

Следовательно, согласно теореме о почленном дифференцировании, ряд

an xn можно почленно дифференцировать, и справедливо равенство (1).

n 0

Следствие.

Степенной ряд на интервале сходимости (-R;R) можно дифференцировать любое число раз.

Теорема.

Степенной ряд an xn можно почленно интегрировать на любом отрезке

n 0

x0;x , принадлежащем интервалу сходимости.

Доказательство аналогично доказательству теореме Абеля и теореме о почленном интегрировании).

Пример.

Найти сумму ряда.

	x	2n 1
( 1)n	x
( 1)n	2n 1
n 0	2n 1

Рассмотрим ряд, полученный почленным дифференцированием:

( 1)x2n 1 x2 x4...

n 0

При |x|<1 – сходится как геометрическая прогрессия

S(x)=	1	;
S(x)=		;
1 x2
[0;x] (-1;1);
Проинтегрируем полученный ряд :
x				x		x	2n 1	x
( 1)n t2ndt			( 1)n t2ndt ( 1)n			x		s(t)dt arctg(x)
( 1)n t2ndt			( 1)n t2ndt ( 1)n					s(t)dt arctg(x)
0 n 0			n 0	0	n 0	2n 1 0

§6. Ряды Тейлора

Пусть функция f(x) имеет в окрестности точки x0 производные любого порядка. Поставим ей в соответствие степенной ряд:


f x f x0 f x0 x x0			f x0		x x 2 ...	f (n) x0	x x0 n ...
		2!
						n!
	f n x				n
		0		x x0		(1)
		n!
n 0

Этот ряд называется рядом Тейлора функции f(x) в точке x0 .

Если x0 0, то ряд Тейлора имеет вид:

f 0 2

(n)

f x f 0 f

...

(2)

n 0

и называется рядом Маклорена.

Радиус сходимости степенного ряда (1) может быть как равным 0, так и отличным от 0, причём в последнем случае сумма S(x) ряда Тейлора может не совпадать с f(x).

412

Необходимо выяснить вопрос о том, когда в соотношении (1) можно поставить знак равенства, то есть когда ряд Тейлора сходится к функции, для которой он составлен.

Если S(x)= f(x) на x0 R;x0 R , то говорят, что функция f(x) разложима в ряд Тейлора в окрестности точки x0 .

Обратимся к следующей теореме.

Теорема 23:

Для того, чтобы бесконечно дифференцируемая в окрестности точки x0 функция f(x) разлагалась в ряд Тейлора в окрестности этой точки, необходимо и достаточно,

что бы lim Rn x 0 для x x0 R;x0 R

Частичные суммы ряда (1) представляют собой многочлены Тейлора Rn x функции f(x)точке x0 . Выпишем последовательность частичных сумм

S0 f x0 ;

S1 f x0 f x0 x x0 ;

S2	f x0	f x0	x x0		f x0	x x0 2 ;

				2!

…………………………………………….

n	f k x	0	k
Sn x		0	x x0
Sn x	k!		x x0
k 0	k!

Если ряд сходится к функции f(x)., справедливо равенство f x Pn x Rn x Sn(x) Rn x

Откуда следует, что

lim Rn x 0

Обратим внимание на то, что в формуле (1) участвует остаточный член ряда Тейлора, а не остаточный член формулы Тейлора. (В общем случае они различны).

Остаток формулы Тейлора представим в одном из следующих видов:

Форма Лагранжа:

	f n 1 c		n
R x		x x		,
R x	n 1!	x x		,
n			0

где c x0;x .

Форма Пеано:

Rn x o x x0 n .

x x0

На практике часто используется следующий достаточный признак разложимости функции в ряд Тейлора:

Теорема 24:

Если для x x0 R;x0 R все производные функции f(x). ограничены одной и той же константой M, то ряд Тейлора (1) сходится к функции f(x).в интервале

x x0 R .

Доказательство:

Возьмём остаточный член формулы Тейлора в форме Лагранжа:

	f n 1 c		c		Rn 1

R x		x x		M
	n 1!				n 1!
n		0

413

При x x0 R;x0 R

Rn 1

Числовой ряд n 1 n 1!– сходится так как

d lim	Rn 2	n 1!	lim	R	0 1.

n n 2 !Rn 1			n n 1

Следовательно, на основании необходимого признака сходимости ряда:

lim	Rn 1	0 lim R x 0	при x x		R;x	R .

n n 1!		n n		0	0

Определение Действительную функцию f(x). действительного переменного называют аналитической в точке x0 , если она определена в некоторой окрестности этой точки, и её можно представить некоторым сходящимся степенным рядом:

f x an x x0 n,

n 0

x x0 ;x0 , 0.

Такое представление аналитической функции называют её разложением в степенной ряд в окрестности точки .

Следующая теорема показывает, что разложение аналитической функции в степенной ряд единственно и этим рядом является её ряд Тейлора.

Теорема. Если в некоторой окрестности точки х для функции f(x). справедливо разложение

f x an x x0 n,

n 0

x x0 ;x0 , 0,

то функция f(x). бесконечно дифференцируема в этой окрестности и

a		f	n x			n 0,1,2,...
			0		;
					;
n			n!
Доказательство:			n!
Доказательство:

Пусть f x an x x0 n,	- некоторое разложение функции f(x). в степенной
n 0
ряд в окрестности x0 ;x0 точки x0				и R радиус сходимости этого ряда. Тогда

x0 ;x0 x0 R;x0 R . Согласно свойствам степенного ряда этот ряд можно

почленно дифференцировать в интервале сходимости x0 R;x0				R любое число
раз. Поэтому для x x0 ;x0	имеем
f x a0 a1 x x0 a2	x x0 2	a3 x x0 3	... an x x0 n ...
То есть	3a3 x
		2	n 1		...
f x a1 2a2 x x0		x0 ... nan x x0			...

f x 2a2 3 2 a3 x x0 2 ... n n 1 an x x0 n 2 ...

………………………………………………………………..

f n x n n 1 n 2 ...1 an n 1 n n 2 ...2 an 1 x x0 ...

Полагая в этих равенствах x x0 получаем:

f x0 a0; f x0 a1;

414

f x0 2a2;

……………………..

f n x0 n!an;

…………………………..

Т.е.

a		f	n x		n 0,1,2,...
	n		0	;
			n!	;

Таким образом, аналитическую в точке x0 функцию можно определить как функцию, которая в некоторой окрестности точки x0 является суммой своего ряда Тейлора.

§7 Разложение элементарных функций в ряд Маклорена

Найдём разложение основных элементарных функций в ряд Маклорена:

1. f (x) ex

так как f n (x) ex;	n N;	x ; . и	f n x	ex	eA , при	x	A, где А -

сколь угодно большое положительное число, следовательно функция f (x) ex - разложима в ряд Маклорена, сходящийся к ней при x R:

f 0 1,

... f

0 1,

f 0

тогда

ex 1

...

(1)

Где x R

n 0

2. f (x) chx

Используя разложение (1), определение f (x) chx

и свойство суммы сходя-

щихся рядов имеем:

x n

1 x

x2n

1 1

chx

, (2)

n 0

2 n 0

n 0

2n !

Где x R .

3. f (x) shx

shx 1 ex e x chx

на основании теоремы о почленном дифференцировании степенного ряда получаем:

			2n			2n 1
		x			x
							(3)
shx
	n 0	2n !		n 1 2n 1!

Где x R .

4. f (x) sin x


		x cosx sin		x ,
f			2

f			x ,
		x sin x sin
		3
	x cosx sin				x ,

f			2

415

x sin x sin

x ,

…………………………………

x sin

sin

x ,

Т.к.

для x R, то функция разложима в ряд Маклорена

sin

f 0 0,

1,...

0 1,

0 0, f

Окончательно получаем

x2n 1

sin x x

... 1

(4)

2n 1!

x R

n 0

2n 1!

f x cosx

Воспользуемся соотношением cosx sin x .

n x2n

x2n

cosx 1

...

... 1

(5)

x R

2n !

n 0

2n !

6. f x ln 1 x

Рассмотрим ряд:

x4 ... 1 n xn

1 x x2

... 1 n xn

n 0

При

это убывающая геометрическая прогрессия, ее сумма S(x)

1 x

1 n tn 1

1 n xn 1

ln 1 x

1 t

(6)

0 1 4

0 n 0

n 0

n 1

n 0

n 1

Для x 1;1 .


7. f x 1 x , где R.
Заметим, что функция и ее производная f		1	удовлетворяют
Заметим, что функция и ее производная f		x 1 x	удовлетворяют
дифференциальному уравнению
1 x f			(7)
1 x f	x f x		(7)

с начальными условиями: f(0)=1;

Решение задачи Коши для дифференциального уравнения единственно, следовательно, если найдётся степенной ряд

1 anxn,

n 1

удовлетворяющий уравнению, то он и будет искомым разложением заданной функции.

1 anxn 1 a1x a2x2 ... anxn ...

n 1

Подставим ряд и его производную в соотношение (7):

1 x a1 2a2x 3a3x2 ... nanxn 1 ...1 a1x a2x2 ... anxn ...

<<< < Предыдущая 1 2 34 / 84 5 6 7 8 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
31.10.2018123.39 Кб316magister-economic-psychology.doc
#
10.02.201579.36 Кб370MakKueyl_D.doc
#
23.03.2016441.86 Кб443Maksakov.doc
#
23.03.20165.38 Mб12208Manipulyatsii_v_SD_Broshyura.doc
#
10.02.20155.14 Mб516matan_3_sem.doc
#
10.02.201517.04 Mб317matan_3_sem.pdf
#
10.02.20151.03 Mб319Maykl_Kan_Mezhdu_Psikhoterapevtom_I_Klientom.doc
#
23.03.2016928.26 Кб331meh_lab БФУ.doc
#
16.08.20191.01 Mб268meh_lab.doc
#
10.02.2015321.54 Кб112Meine Sommerferien.doc
#
17.04.2019252.74 Кб28menedzhment_otvety.docx