билеты пдф

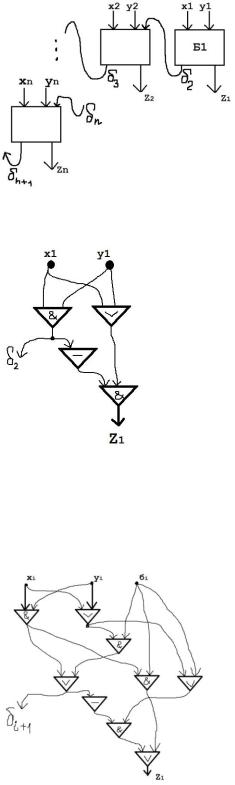
Блоки.

Блок Б1.

L(Б1)=4.

Бi, i

Сложность: L(Бi)=9.

БИЛЕТ 38 Логика высказываний.

Логика высказываний — это определённая совокупность формул, т.е. сложных высказываний, записанных на специально сконструированном искусственном языке. Язык логики высказываний включает:

1.неограниченное множество переменных: А, В, С, …, А1 , В1 , С1 , …, представляющих высказывания;

2.особые символы для логических связок: & — «и», v — «или», V — «либо, либо», ? — «если, то», ? — «если и только если», ~ — «неверно, что»»

3.скобки, играющие роль знаков препинания обычного языка. Чтобы использовать меньшее количество скобок, условимся, что операция отрицания выполняется первой, затем идут конъюнкция и дизъюнкция, и только после этого импликация и эквивалентность.

Формулам логики высказываний, образованным из переменных и связок, в естественном языке соответствуют предложения. К примеру, если А есть высказывание «Сейчас день», В — высказывание «Сейчас светло» и С — высказывание «Сейчас холодно», то формула: А ? В v С , или со всеми скобками: (А ? (В v С)) ,

представляет высказывание «Если сейчас день, то сейчас светло или холодно». Формула:

В & С ? А , или ((В & С) ? А) ,

представляет высказывание «Если сейчас светло и холодно, то сейчас день». Формула: ~ В ? ~ А , или ((~ В) ? (~ А)) ,

представляет высказывание «Если неверно, что сейчас светло, то неверно, что сейчас день» и т.п. Подставляя вместо переменных другие конкретные (истинные или ложные) высказывания, получим другие переводы указанных формул на обычный язык. Формула, которой не соответствует осмысленное предложение, построена неправильно. Таковы, в частности, формулы:

(А ?), ( & В), (A v ВС), ( ~ & ) и т.п.

Каждой формуле логики высказываний соответствует таблица истинности, показывающая, при каких подстановках конкретных высказываний в данную формулу она даёт истинное сложное высказывание, а при каких ложное. Например, формула (~ В ? ~ А) даст ложное высказывание, только если вместо В подставить ложное высказывание, а вместо А — истинное.

Всегда истинная формула логики высказываний, или тавтология, — это формула, дающая истинное высказывание при любых подстановках, в неё конкретных (т.е. истинных или ложных) высказываний.

Иными словами, внутренняя структура тавтологии гарантирует, что она всегда превратится в истинное высказывание, какими бы конкретными высказываниями мы ни заменяли входящие в неё переменные.

Всегда ложная формула, или логическое противоречие, всегда превращается влажное высказывание при подстановке конкретных высказываний вместо её переменных.

БИЛЕТ 39 Логическое следствие.

Определение 1. Формула B называется логическим следствием формул A1, A2, …, An, если при любых значениях, входящих в них, элементарных высказываний формула B принимает значение истинно всякий раз, когда формулы A1, A2, …, An принимают значение истинно. Обозначается A1, A2, …, An ¦ B

Из определения логического следования вытекает: Тавтология логически следует из любой формулы. Из противоречия логически следует любая формула.

Теорема 1. Из A логически следует B тогда и только тогда, когда тавтологией является AB. Теорема 2. A1, A2,…, An¦ B тогда и только тогда, когда является тавтологией

A1&A2& …& An B.

Теорема 3. Из формул A1, A2,…, An , B логически следует C тогда и только тогда, когда из формул A1, A2, …, An логически следует BC.

Следствие 1. Из A и B логически следует C тогда и только тогда, когда тавтологией является

A (BC).

Следствие 2. Из формул A1, A2, …, An логически следует B тогда и только тогда, когда тавтологией является

A1 (A2 … (AnB)…).

Отношение логического следования играет в математике большую роль.

Если из A¦B, то A называется достаточным условием для B, а B - необходимым условием для A.

Если вместе с A¦B из B¦A, то A называется необходимым и достаточным условием для B, а B - необходимым и достаточным условием для A.

превращается в истинное высказывание при всякой такой подстановке вместо всех ее

Наконец можно и так сказать о логическом следствии. Составим таблицы истинности для

принимает значение 1. Это и будет означать, что 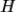является логическим следствием формул .

Из сформулированного определения вытекает четкий алгоритм проверки формул на логическое следование (далее приводится в виде схемы). Рассмотрим его действие для случая, например, трех формул-посылок, зависящих от трех переменных:

Все эти формулы должны быть заданы таблицей своих значений:

БИЛЕТ 40 Логические высказывания и булевы функции.

Под высказыванием (суждением) понимают форму мысли, которая выражает соответствие или несоответствие ее действительности. Высказывание может быть истинным или ложным. Из одних высказываний можно получить другие с помощью логических связок (&, v). Каждому высказывании соответствует булева переменная, каждой логической связке – булева операция. Высказывания могут быть истинными и ложными. Также есть логические связки.

А => B. Из А логически следует высказывание В, если всякий раз когда А истинно, В тоже истинно.

(А1, …, An) =>B. Логически следует В, если (А1, …, An) – истинно, и В тоже истинно.

A => B  (A -> B) 1.

(А1, …, An)=> B ((А1 & …& An) -> B) 1.

БИЛЕТ 41 Основная теорема теории логического вывода.(продолжение билета 40)

(A -> B) = v B

A & (доказательство от противного).

БИЛЕТ 42 Графы. Основные определения.

Графом G называется совокупность двух множеств: вершин V и ребер E , между элементами которых определено отношение инцидентности – каждое ребро e E

инцидентно ровно двум вершинам v ,v V , которые оно соединяет. При этом вершина

v (v ) и ребро e называются инцидентными друг другу, а вершины v ,v , являющиеся для ребра концевыми точками, называются смежными. Именно отношение инцидентности является самым важным элементом графа, т. к. определяет способ

объединения множеств V и E в единый графический объект.

Ребро, соединяющее две вершины, может иметь направление от одной вершины к другой;

в этом случае оно называется направленным, или ориентированным, или дугой, и

изображается стрелкой, направленной от одной вершины (начала) к другой (концу). Граф, содержащий дуги, называется ориентированным, или орграфом. Граф,

Ребра, инцидентные одной и той же паре вершин, называются кратными. Граф, содержащий кратные ребра, называется мультиграфом. Ребро, концевые вершины которого совпадают, называется петлей.

Вершина, не инцидентная ни одному ребру, называется изолированной. Граф может состоять только из изолированных вершин. В этом случае он называется нуль-графом.

Граф без петель и кратных ребер называется полным, если каждая пара вершин соединена ребром.

Дополнением графа G называется граф G , имеющий те же вершины, что и граф G , и

содержащий только те ребра, которые нужно добавить к графу G , чтобы получить полный граф.

Каждому неориентированному графу соответствует ориентированный граф с тем же множеством вершин, в котором каждое ребро заменено двумя дугами, инцидентными тем же вершинам и имеющим противоположные направления.

сумма степеней всех вершин равна удвоенному числу ребер m графа, т. е. четна, если считать, что петля дает вклад 2 в степень вершины:

Сумма степеней вершин любого графа равна удвоенному числу его ребер. Отсюда следует, что в н-графе число вершин нечетной степени четно.

БИЛЕТ 43 Способы задания графов.

*учебник*

{

Наиболее простым и естественным способом задания графа является графический. Однако таким образом можно задать только небольшие графы, к тому же он неудобен для автоматизированной обработки и передачи графической информации. Рассмотрим другие способы, используемые в теории графов.

В общем виде задать граф – значит описать множества его вершин и ребер, а также отношение инцидентности. Для описания вершин и ребер их достаточно занумеровать.

Пусть v1,v2 ,. ..,vn – вершины графа G ; e1,e2 ,. . . ,em – ребра. Отношение инцидентности может быть задано следующими способами:

указываются вершины и ребра соответственно, а на пересечении i -й вершины и j -го ребра, в случае неориентированного графа, проставляется 1, если они инцидентны, и 0 – в противоположном случае, т. е.

а в случае орграфа: –1, если вершина является началом дуги; 1 – если вершина является концом дуги и 0 – если вершины не инцидентны. Если некоторая вершина является для ребра и началом и концом (т. е. ребро – петля), проставляется любое другое число, например 2.

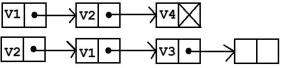
2. Списком ребер графа, представленным двумя столбцами: в левом перечисляются

все ребра e E , в правом – инцидентные им вершины (v , v ) . Для н-графа порядок вершин произволен, для орграфа первым стоит номер начала дуги. При наличии в графе изолированных вершин они помещаются в конец списка.

горизонтали перечисляются все вершины, а на пересечении k -й и l -й вершин, в случае н-графа, проставляется число k l , равное числу ребер, соединяющих эти вершины. Для

орграфа k l равно числу ребер с началом в k -й вершине и концом в l -й вершине.

}

6)Списки смежности;

V1: V2: V4; V2: V1; V3; V4; V3: V2;

V4: V1; V2; V5: .

7)Структуры смежности - компьютрное представление списков смежности.

БИЛЕТ 44 Изоморфизм графов. Необ одимые условия изоморфизма графов.

*лекции*

Определение. Два графа G1=(V1,E1) и G2=(V2,E2) называются изоморфными, если существует взаимно-однозначное соответствие V1 и V2, сохраняющее отношение инцедентности.

Задачи в теории графов ставятся и решаются с точностью до изоморфизма графов. Разновидности графов.

1)Ориентированный

Пример. Транспортные сети.

2)Мультиграфы – графы, в которых допускается несколько ребер одного направления.

3)Псевдографы – мультиграфы, в которых допускаются петли.

Степень – количество ребер инцедентных вершин. Вершины степени 0 называются изолированными. Вершина степени один называется висячей.

Маршрутом в графе G называется последовательность вершин и ребер.

M=(V0,e1,V1,e2,V2,…), где ei=(Vi-1,Vi) соединяет Vi-1 и Vi.

М=(V0,Vk), где k-маршрута.

Граф называется связанным, если для любой пары вершин существует маршрут, соединяющий их.

БИЛЕТ 45 Геометрическая реализация графов

*лекции*

{

Пусть – евклидовое n-мерное пространство. Геометрическим графом называют Г=(V,E), где V - множество вершин (точек в этом евклидовом пространстве), Е – множество ребер. Геометрические графы не должны иметь самопересечений и взаимных пересечений.

Теорема. Любой конечный граф можно представить в виде геометрического графа в трехмерном евклидовом пространстве.

Доказательство.

Пусть G=(V,E) – трехмерный абстрактный граф. Построим аналог:

V = {V1,…,Vp} E = {e1,…eq}

Г = (V’,E’) – изоморфность G.

Через прямую L проводим q полуплоскостей (число q конечное). Для каждого ребра ej выберем свою полуплоскость ej = (а,b). Если a≠b, то проводим полуокружность. Если а=b, то в этой полуплоскости проводим окружность единичного радиуса, который касается прямой l в точке а. По построению видим, что Г – геометрический граф, потому что каждая линия лежит в своей полуплоскости, т.е. G Г.

}

БИЛЕТ 46 Планарные графы. Критерий планарности графов.

Говорят, что граф G укладывается на плоскости, т. е. является планарным, или плоским, если его можно нарисовать так, что его ребра будут пересекаться лишь в концевых точках – вершинах. Изображение планарного графа на плоскости называется планарной укладкой. Определение планарности графов имеет большое практическое значение. Достаточно привести задачу разводки печатных плат, когда необходимо избежать пересечения проводников в местах, не предназначенных для соединений. Если изобразить места указанных соединений как вершины графа, то возникнет задача построения графа с непересекающимися ребрами. Важно отметить, что интерес представляет именно возможность построения графа с непересекающимися ребрами.

Графы Куратовского считаются основными непланарными графами потому, что играют решающую роль в исследовании планарности графов.

Рис. 3.21. Непланарные графы (графы Куратовского): a – граф K 5 ;

б – граф K3,3

Теорема Понтрягина-Куратовского. Граф планарен тогда и только тогда, когда он не

содержит в качестве подграфа графа K 5 или Утверждение: Полный граф K – не планарен.

Доказательство: допустим противное – граф K планарен и G есть его плоская укладка. Т.к. граф K и G изоморфны, то каждое ребро G есть 3-цикл. Положим n=3, p= , q=10, получаем 10 ≤ 3*(5-2) / (3-2) = 9 что противоречит условию граф K – не планарен.

Утверждение: Граф K3,3 – не планарен.

Доказательство: допустим противное: граф K3,3 – планарен и имеет плоское изображение G, т.к. K3,3 и G изоморфны, то каждая грань в G есть 4-цикл. Подставляем в формулу следующие значения n=4, p=6, q=9, получаем 9 ≤ 4(6-2) / (4-2) = 8 противоречие K3,3 – не планарен.

БИЛЕТ 47 Деревья. Корневые деревья.

Деревом называется связный граф без циклов. Граф без циклов называется лесом. Разновидности деревьев:

1)Корневые деревья. Выделение корня – разбиение дерева на ярусы и определение ориентации ребер от корня. Используется понятие сыновей и потомков.

2)Упорядоченные деревья. Для каждой вершины задается порядок среди смежных с ней вершин.

3)Бинарные деревья. У каждой вершины либо нет сыновей, либо 2 сына, либо 1.

Элементарные свойства деревьев:

1)Удаление висячей вершины в дереве приводит снова к дереву.

2)При добавлении любого ребра к дереву соединяющего вершину образуется цикл.

3)В любом не тривиальном дереве имеется по крайней мере 2 висячие вершины.

4)Для любого дерева T : q(T)=P(T)-1.

Из другого источника:

Определение 1. Любое дерево, в котором выделена одна вершина, называемая корнем, называется корневым деревом.

Определение 2. 1) Граф, состоящий из одной вершины, которая выделена, называется корневым деревом.

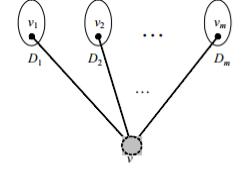
2) Пусть имеются корневые деревья D1, D2, …, Dm с корнями v1, v2, …, vm, Di = (Vi, Ei),

и в котором выделена вершина v, называется корневым деревом.

3) Только те объекты являются корневыми деревьями, которые можно построить согласно пунктам 1) и 2).

При таком определении D1,D2,…,Dm называются поддеревьями дерева D.

Определение 3. Упорядоченным корневым деревом называется корневое дерево, в котором

1)задан порядок поддеревьев и

2)каждое поддерево Di является упорядоченным поддеревом.

Дерево с одной вершиной также является упорядоченным поддеревом.

БИЛЕТ 48 Задачи о кратчайши путя в графа .

Алгоритм Дейкстры (англ. D jkstra’s algor th ) — алгоритм на графах, изобретённый нидерландским ученым Э. Дейкстрой в 19 9 году. Находит кратчайшее расстояние от одной из вершин графа до всех остальных. Алгоритм работает только для графов без рёбер отрицательного веса.

Неформальное объяснение

Каждой вершине из V сопоставим метку — минимальное известное расстояние от этой вершины до a. Алгоритм работает пошагово — на каждом шаге он «посещает» одну вершину и пытается уменьшать метки. Работа алгоритма завершается, когда все вершины посещены.

Инициализация. Метка самой вершины a полагается равной 0, метки остальных вершин — бесконечности. Это отражает то, что расстояния от a до других вершин пока неизвестны. Все вершины графа помечаются как непосещённые.

Шаг алгоритма. Если все вершины посещены, алгоритм завершается. В противном случае, из ещё не посещённых вершин выбирается вершина u, имеющая минимальную метку. Мы рассматриваем всевозможные маршруты, в которых u является предпоследним пунктом. Вершины, в которые ведут рёбра из u, назовем соседями этой вершины. Для каждого соседа вершины u, кроме отмеченных как посещённые, рассмотрим новую длину пути, равную сумме значений текущей метки u и длины ребра, соединяющего u с этим соседом. Если полученное значение длины меньше значения метки соседа, заменим значение метки полученным значением длины. Рассмотрев всех соседей, пометим вершину u как посещенную и повторим шаг алгоритма.

БИЛЕТ 49 Задача о минимальном остовном дереве.

Постановка задачи

Итак, имеется n городов, которые нужно объединить в единую телефонную сеть. Для этого достаточно проложить (n-1) телефонных линий между городами. Как соединить города так, чтобы суммарная стоимость соединений (телефонного кабеля) была минимальна?

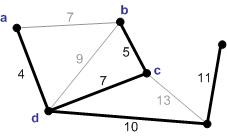
В общем случае, задачу можно сформулировать так. Пусть дан связный, неориентированный граф с весами на ребрах G(V, E), в котором V — множество вершин (контактов), а E — множество их возможных попарных соединений (ребер). Пусть для каждого ребра (u,v) однозначно определено некоторое вещественное число w(u,v) — его вес (длина или стоимость соединения). w() называется весовой функцией. Задача состоит в нахождении такого связного ациклического подграфа T G, содержащего все вершины, что суммарный вес его ребер будет минимален.

Так как T связен и не содержит циклов, он является деревом и

называется остовным или покрывающим деревом (spanning tree). Остовное дерево T, у которого суммарный вес его ребер w(T) = ∑(u,v) T w(u,v) минимален, называется минимальным остовным или минимальным покрывающим деревом (minimum spanning tree).

Суммарный вес дерева = 37. Это минимальное остовное дерево не уникально: удалением ребра (c,d) и добавлением ребра (a,b) получается новое минимально остовное дерево.

Так как рассматриваются только деревья, можно считать все ребра положительными (достаточно добавить к весу всех ребер некоторую относительно большую положительную константу). В противном случае, если стоимость соединения между двумя вершинами равна отрицательному числу, можно несколько раз параллельно соединить их для уменьшения суммарного веса остовного подграфа.