билеты пдф

12) Законы полезные для упрощения x ˅ (x * y) = x –закон поглощения

x & (x ˅ y) = x

x ˅ ( x * y) = x ˅ y

x & y + x & y = x – закон склеивания

Особенность данных эквивалентных соотношений в том, что:

·они не выводимы друг из друга. Убедиться в их справедливости можно путем построения таблиц истинности; ·этих соотношений достаточно для выполнения любых эквивалентных преобразований.

БИЛЕТ 24 Связь между алгеброй множеств и алгеброй логики.

Пусть имеется система множеств x1,x2,…,xn,и определены операции над множествами. Мы можем

На примере закона Де Моргана.

(1)

˄(2)

M’ M”

Связь между алгеброй множеств и алгеброй логики заключается в том, что есть 2 изоморфные системы.

БИЛЕТ 25 Понятие двойственности. Принцип двойственности.

Опр. Для заданной булевой функции двойственной к ней называют: ).

Замечания.

1)

Замечание. В функциях fi, i=1,…,m некоторые переменные могут быть фиктивными. Тогда

=

]

Следствие. Если задана булева функция формулой F в базисе Б0=(x&y,x˅y,-,0,1), то для получения двойственной функции достаточно сделать замену:

(&,˅,-,0,1) (˅,&,-,1,0)

БИЛЕТ 26 Разложение булевы функций по переменным.

Т. о разложении булевой функции по переменным.

Для любой булевой функции f=f(x1,…,xn) и V 1≤k≤n справедливо представление f(x1,…,xn)= , где x1=x, x0= x.

Возьмем произвольный набор Z=(α1,…,αn) и подставим в левую и правую части формулы:

Л.Ч.=f(α1,…,αn)

Следствие1. Формула разложения булевой функции по переменным: Положим k=1. Возьмем разложение по последней переменной.

Следствие2. Разложение функции в совершенную дизъюнктивную нормальную формулу (СДНФ). V справедливо = .

=1.

Возьмем в теореме случай k=n, т.е. разложение по всем переменным.

Следствие3. О представимости любой функции в классическом базисе. Любую булеву функцию можно представить в виде формулы над базисом.

представление является единственной.

БИЛЕТ 27 Совершенные дизъюнктивные нормальные формы (СДНФ)[сумма произведений ˅&].

Система операций булевой алгебры полна, и переход от табличного задания любой логической функции к формуле булевой алгебры всегда возможен. Сформулируем очень важный для практики способ перехода от табличного задания логической функции к булевой формуле. Он включает следующие действия:

·для каждого набора значений переменных x1, x2 ,..., xn , на котором функция f (x1, x2 ,..., xn ) равна 1, выписываются конъюнкции всех переменных; ·над теми переменными, которые на этом наборе равны 0, ставятся отрицания; ·все такие конъюнкции соединяются знаками дизъюнкции.

Полученная таким образом формула называется совершенной дизъюнктивной нормальной формой (СДНФ) логической функции.

Для каждой функции СДНФ единствена.

Таким образом, СДНФ функции f (x1, x2 ,..., xn ) представляет собой дизъюнкцию элементарных конъюнкций: D = K1 ˅ K2 ˅ ... ˅ Km, где все конъюнкции имеют одинаковое число сомножителей, равное числу логических переменных, а число конъюнкций равно числу наборов значений переменных x1, x2 ,..., xn , на которых функция f (x1, x2 ,..., xn) равна 1. Любые другие записи логической функции, вида D = K1 ˅ K2 ˅ ... ˅ Km, не отвечающие этим условиям, называются дизъюнктивными нормальными формами (ДНФ) этой функции.

БИЛЕТ 28 Совершенные конъюнктивные нормальные формы (СКНФ)[произведение сумм &˅].

Утверждение. Для любой булевой функции f=f(x1,…,xn),f≠1 справедливо представление

Имеем: f*≠ 0. Теперь построим СДНФ для f*.

=

Возьмем двойственную от обеих частей уравнения.

=

СКНФ и это представление является единственным.

БИЛЕТ 29 Полиномы Жегалкина.

В алгебре логики обычно выделяют 3 кононические формы представления функции в виде формулы:

Полином Жегалкина:

P=M1 M2 … Mk, Mi – моном.

Все мономы попарно различны.

Теорема. Любую булеву функцию можно представить в виде полинома Жегалкина и это представление является единственным.

[

I. Доказываем представимость функции в виде полинома Жегалкина. Рассмотрим 2 случая

1)f ≡ 0, F=0

2)f ≠ 0, тогда

Раскрываем скобки, приводим подобные по правилу А А=0.

В итоге получим полином Жегалкина для каждой функции существует полином Жегалкина. II. Доказываем единственность.

Воспользуемся принципом Дирихле. Подсчитаем количество полиномов Жегалкина.

. То есть 2n отличных от нуля.

Пустой моном=1.

Образуем полином: Мономов = N=2n

Полиномов = 2N=

Если ничего не включили, то 0.

| ]

БИЛЕТ 30 Понятие функциональной полноты системы булевы функций. Полнота системы {И, ИЛИ, НЕ}.

Определение. Множество функций алгебры логики А называется полной системой (в Р2), если любую функцию алгебры логики можно выразить формулой над А.

Теорема. Система А = {v, &, ─} является полной.

Доказательство. Если функция алгебры логики f отлична от тождественного нуля, то f выражается в виде совершенной дизъюнктивной нормальной формы, в которую входят лишь дизъюнкция, конъюнкция и отрицание. Если же f≡ 0, то f = x*(─x). Теорема доказана.

БИЛЕТ 31 Замыкание и замкнутые классы.

1°. Понятие замкнутого класса.

Определение 1. Пусть A P2. Тогда замыканием A называется множество всех функций алгебры логики, которые можно выразить формулами над A.

Обозначение: [A].

Имеют место следующие свойства:

1)[A] A;

2)A B [A] [B], причём, если в левой части импликации строгое вложение, то из него вовсе не следует строгое вложение в правой части — верно лишь A B [A] [B];

3)[[A]] = [A].

Определение 2. Система функций алгебры логики A называется полной, если [A] = P2. Определение 3. Пусть A P2. Тогда система A называется замкнутым классом, если замыкание A совпадает с самим A: [A] = A.

2°. Примеры замкнутых классов.

Класс T0 = {f (x1, …, xn) | f (0, …, 0) = 0}.

Классу T0 принадлежат, например, функции 0, x, xy, x y, x y. Классу T0 не принадлежат функции 1, x , x → y, x | y, x ↓ y, x ~ y.

Класс T1 = {f (x1, …, xn) | f (1, 1, …, 1) = 1}.

Классу T1 принадлежат функции 1, x, xy, x y, x → y, x ~ y. Классу T1 не принадлежат функции 0, x , x y, x | y, x ↓ y. Класс L линейных функций.

Определение 4. Функция алгебры логики f (x1, …, xn) называется линейной, если f (x1, …,xn) = a0 a1 x1 … an xn, где ai {0, 1}.

Иными словами, в полиноме линейной функции нет слагаемых, содержащих конъюнкцию. Классу L принадлежат функции 0, 1, x = x 1, x ~ y, x y.

Классу L не принадлежат функции xy, x y, x → y, x | y, x ↓ y. Класс S самодвойственных функций.

Определение 2. Функция алгебры логики f (x1, …, xn) называется самодвойственной, если f (x1,…,

xn) = f* (x1,…,xn).

Иначе говоря, S = {f | f = f*}.

Определение 2. Функция алгебры логики f (x1,…,xn) называется монотонной, если для любых двух сравнимых наборов ~α и ~β выполняется импликация ~α≤ ~ β f(~α) ≤ f (~ β)

Класс M всех монотонных функций.

Классу M принадлежат функции 0 , 1 , x , xy , x y, m (x, y, z) = xy yz zx. Классу M не принадлежат функции x , x | y , x ↓ y , x y , x ~ y , x → y

БИЛЕТ 32 Классы Поста.

Критерий Поста — одна из центральных теорем в теории булевых функций, устанавливающая необходимое и достаточное условие для того, чтобы некоторый набор булевых функций обладал достаточной выразительностью, чтобы представить любую булеву функцию. Впервые сформулирован американским математиком Эмилем Постом.

Булева функция — это функция типа , где , а 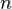— арность. Количество

различных функций арности равно , общее же количество различных булевых функций бесконечно. Вместе с тем, очевидно, что многие функции могут быть выражены через другие с использованием оператора суперпозиции. Например, давно известно, что из дизъюнкции и отрицания можно, используя законы де Моргана, получить конъюнкцию. Кроме того, любая булева функция (за исключением тождественного нуля) может быть представлена в виде ДНФ, то есть, в терминах конъюнкции, дизъюнкции и отрицания. Возникает естественный вопрос: как определить, будет ли данный набор функций достаточным, чтобы представить любую булеву функцию? Такие наборы называются функционально полными. Теорема Поста даёт ответ на этот вопрос. Поскольку условие теоремы является необходимыми и достаточным, её называют также критерием.

Идея теоремы состоит в том, чтобы рассматривать множество всех булевых функций как алгебру относительно операции суперпозиции. Сейчас она носит имя алгебра Поста. Эта алгебра содержит в качестве своих подалгебр множества функций, замкнутых относительно

суперпозиции. Их называют ещё замкнутыми классами. Пусть — некоторое подмножество

.Замыканием множества 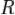называется минимальная подалгебра , содержащая . Иными словами, замыкание состоит из всех функций, которые являются суперпозициями . Очевидно,

что будет функционально полно тогда и только тогда, когда . Таким образом, вопрос, будет ли данный класс функционально полон, сводится к проверке того, совпадает ли его замыкание с .

БИЛЕТ 33 Критерий полноты.

Теорема 12 (теорема Поста). Система функций алгебры логики A = {f1, f2, …} является полной в P2 тогда и только тогда, когда она не содержится целиком ни в одном из следующих классов: T0,

T1, S, L, M.

Доказательство. Необходимость. Пусть A — полная система, N — любой из классов T0, T1, S, L, M и пусть A N. Тогда [A] [N] = N ≠ P2 и [A] ≠ P2. Полученное противоречие завершает обоснование необходимости.

Достаточность. Пусть A T0, A T1, A M, A L, A S. Тогда в A существуют функции f0 T0, f1

T1, fm M,

fl L, fs S. Достаточно показать, что [A] [f0, f1, fm, fl, fs] = P2. Разобьём доказательство на три части: получение отрицания, констант и конъюнкции.

a) Получение ─x . Рассмотрим функцию f0 (x1, …, xn) T0 и введём функцию φ0(x) =f0(x, x, …, x). Так как функция f0 не сохраняет нуль, φ0(0) = f (0, 0, …, 0) = 1. Возможны два случая: либо ϕ0(x)

= ─x , либо φ0 (x) ≡ 1. Рассмотрим функцию f1(x1, …, xn) T1 и аналогичным образом введём функцию φ1(x) = f1(x, x, …, x). Так как функция f1 не сохраняет единицу, φ1(1) = f (1, 1, …, 1) = 0. Возможны также два случая: либо ϕ1( x) = ─x , либо φ1 (x) ≡ 0. Если хотя бы в одном случае получилось искомое отрицание, пункт завершён. Если же в обоих случаях получились константы, то согласно лемме о немонотонной функции, подставляя в функцию fm M вместо всех переменных константы и тождественные функции, можно получить отрицание.

Отрицание получено.

b)Получение констант 0 и 1. Имеем fs S. Согласно лемме о несамодвойственной функции, подставляя вместо всех переменных функции fs отрицание (которое получено в пункте a) и тождественную функцию, можно получить константы: [fs, x ] [0, 1]. Константы получены.

c)Получение конъюнкции x · y. Имеем функцию fl L. Согласно лемме о нелинейной функции, подставляя в функцию fl вместо всех переменных константы и отрицания (которые были получены на предыдущих шагах доказательства), можно получить либо конъюнкцию, либо отрицание конъюнкции. Однако на первом этапе отрицание уже получено, следовательно, всегда можно получить конъюнкцию:

[fl, 0, 1, ─x ] [xy, ─xy]. Конъюнкция получена.

В результате получено, что [f0 , f1 , fm , fl, fs] [ ─x,xy] = P2 . Последнее равенство следует из пункта 2 теоремы 4. В силу леммы 2 достаточность доказана.

БИЛЕТ 34 Реализация булевы функций с емами из функциональны элементов.

*учебник*

{

Одно из основных приложений булевых функций лежит в области создания схем функциональных элементов или функциональных схем, которые можно реализовать в виде электронных устройств с конечным числом входов и выходов, причем на каждом входе и выходе может появляться только два значения. Такие устройства собраны из функциональных элементов, генерирующих основные булевы операции.

Соединяя функциональные элементы вместе, мы получаем функциональную схему. С ее помощью можно реализовать любую булеву функцию.

Сложностью схемы из функциональных элементов называется число функциональных элементов в схеме.

}

*лекции* Дизъюнктор, инвектор.

СФЭ – схемы из функциональных элементов.

F=(f1, f2, …, fm)

L(S) – сложность – количество функциональных элементов в схеме.

L(S) = minL(S) – наименьшее количество элементов, с помощью которых можно построить схему. LA(f) = L(SA(f)) – сложность схемы.

LA(n) = maxLA(f), f ϵ . Макс.берется по всем переменным. Функция Шеннона для А.

L(f) = minL(S) L(n) = maxL(f) LA(n) L(n)

Пусть в СДНФ l (эль) слагаемых. f = k1˅k2˅…˅kl

Обозначим полученную схему S, тогда

L(S) = L(Dn)+L(Vl)

L(Dn) = 2*2n + n – 4 l ≤ 2n

L(Vl)=l - 1≤ 2n – 1

L(S) ≤ (2*2n + n - 4) + (2n - 1) = 3*2n + n – 5.

БИЛЕТ 35 Реализация дешифратора в классе с ем из функциональны элементов (с ема для выборки элементов).

*учебник*

{

Дешифратором Qn порядка n называется схема из функциональных элементов с n входами x1, x2, …, xn и 2n выходами z0, z1,…, такая, что если |x1x2…xn| = i, то zi = 1 и zj = 0 при i ≠ j.

Заметим, что если i = (i1, i2, …, in)2, то zi(x1,…,xn ) = .

Лемма. Существует дешифратор Qn с числом элементов, не превосходящим n2n+1. Доказательство. Для реализации каждой zi достаточно взять ровно n–1 конъюнкций и не более n отрицаний, то есть всего менее, чем 2n функциональных элементов. Всего различных конъюнкций ровно 2n, и сложность дешифратора не превосходит n2n+1.

}

*лекции*

k0 = k1 = k2 = k3 =

Тривиальные методы основаны на автономной реализации элементарных конъюнкций.

БИЛЕТ 36 Универсальные методы синтеза с ем из функциональны элементов.

Теорема. Существует метод синтеза схем из функциональных элементов такой, что для любой булевой функции f(x1,…,xn) строится ее реализующая схема S, такая, что

L(S) ≤ 3*2n + n – 5 , отсюда:

Следствие. L(n) ≤ 3*2n + n – 5 Замечание.

БИЛЕТ 37 Реализация двоичного сумматора в классе с ем из функциональны элементов.

*учебник*

{

Определение. Сумматором Sn порядка n называется схема с 2n входами x1, x2, …, xn, y1, y2, …, yn и

n + 1 выходом z0, z1, z2, …, zn такая, что |z| = |Sn(x,y)| = |x|+|y|.

Теорема. Существует схемный сумматор порядка n в базисе {˅, &, } с числом элементов 9n – 5. Доказательство. Построим искомый схемный сумматор. Для этого возьмём одну ячейку полусумматора, содержащую четыре элемента и n–1 ячейку сумматора, каждая из которых содержит девять элементов. Построим из этих частей сумматор.

}

*лекции* Пусть имеются два числа, записанные в двоичном виде. x =