
ConspectiLekziiMexanika2013-2
.pdf
Закон сохранения энергии в механике
Рассмотрим систему из n материальных точек, на которые действуют силы. Работа консервативных сил может быть
представлена как убыль потенциальной энергии системы 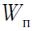 :
:
 .
.
Работу неконсервативных сил обозначим А*.
Суммарная работа всех сил затрачивается на приращение кинетической энергии системы 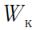 , следовательно,
, следовательно,
или
. (78)
Сумма кинетической и потенциальной энергии представляет собой полную механическую энергию Е системы:
. |
(79) |
Таким образом
. |
(80) |
Очевидно, что если неконсервативные силы в системе отсутствуют, что означает 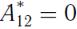 , то ее полная механическая энергия остается постоянной (сохраняется) т.е. Е = const.
, то ее полная механическая энергия остается постоянной (сохраняется) т.е. Е = const.
Эту теорему называют законом сохранения механической энергии,
он утверждает: полная механическая энергия системы материальных точек, находящихся под действием консервативных сил остается постоянной.
61
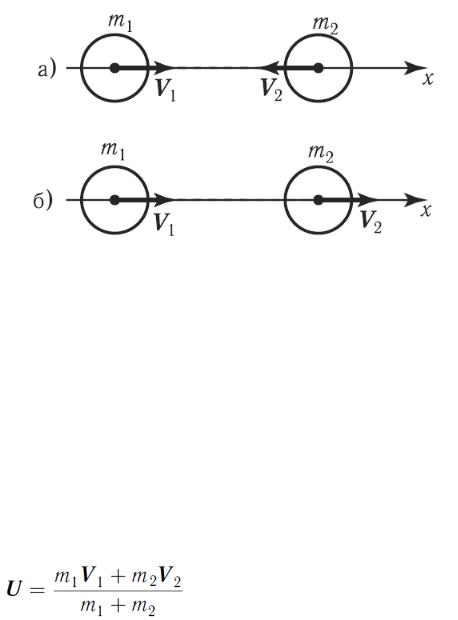
Упругое и неупругое соударения
При соударении тел они деформируются. При этом кинетическая энергия тел частично или полностью переходит в потенциальную энергию упругой деформации и во внутреннюю энергию тел.
Рассмотрим центральные удары двух шаров, при которых они направлены вдоль прямой, проходящей через их центры (рис. 32).
Рисунок 32.
Абсолютно неупругий удар
После такого удара тела движутся с одинаковыми скоростями. При этом выполняется только закон сохранения суммарного импульса тел:
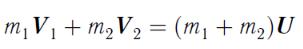 ,
,
Откуда |
. |
(81) |
Изменение кинетической энергии определим как (без вывода):
62
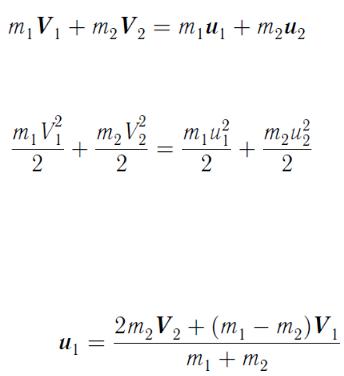
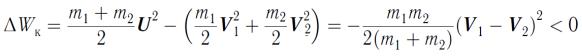 . (82)
. (82)
Абсолютно упругий удар
Это такой удар, при котором полная механическая энергия тел сохраняется.
В итоге потенциальная энергия упругой деформации снова переходит в кинетическую и тела разлетаются со скоростями, которые определяются исходя из законов сохранения суммарного импульса и полной механической энергии системы.
Обозначим массы шаров m1 и m2, скорости шаров до удара 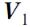 и
и 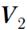 , скорости шаров после удара
, скорости шаров после удара 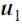 и
и 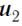 и тогда:
и тогда:
(сохранение суммарного импульса)
(сохранение механической энергии) |
(83). |
Найдем скорости шаров после абсолютно упругого удара (без вывода):
(84)
и
63
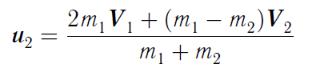
. (85)
64
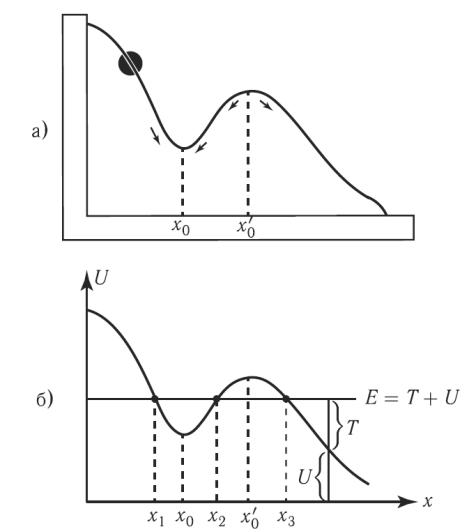
Равновесие системы. Потенциальные кривые
Рисунок 33.
Область х1 - х2 – потенциальная яма, х0 – минимальное значение
потенциальной энергии в этой области; х2 – х3 – потенциальный барьер, для преодоления которого необходима дополнительная энергия.
65
Движение твердого тела
Момент силы и момент импульса
Пусть О - какая-либо неподвижная точка в инерциальной системе отсчета. Обозначим через 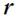 радиус-вектор, проведенный из этой точки к точке приложения силы
радиус-вектор, проведенный из этой точки к точке приложения силы 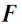 .
.
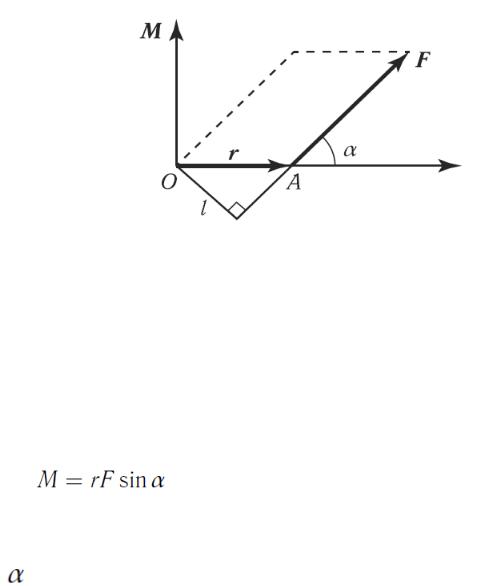
Рисунок 34.
Моментом силы 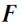 относительно точки О называется векторное произведение радиуса-вектора
относительно точки О называется векторное произведение радиуса-вектора 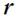 на силу
на силу 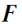 (рис. 34):
(рис. 34):
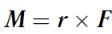 .
.
Модуль момента силы определяется как
(86),
где:
- угол между векторами 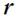 и
и 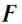 , l – плечо силы; направление
, l – плечо силы; направление
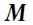 выбирается так, чтобы последовательность векторов
выбирается так, чтобы последовательность векторов 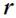 ,
, 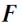
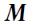 , образовывала правовинтовую систему.
, образовывала правовинтовую систему.
66
Моментом 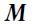 нескольких сил относительно точки называется векторная сумма моментов этих сил относительно той же точки
нескольких сил относительно точки называется векторная сумма моментов этих сил относительно той же точки
. |
(87) |
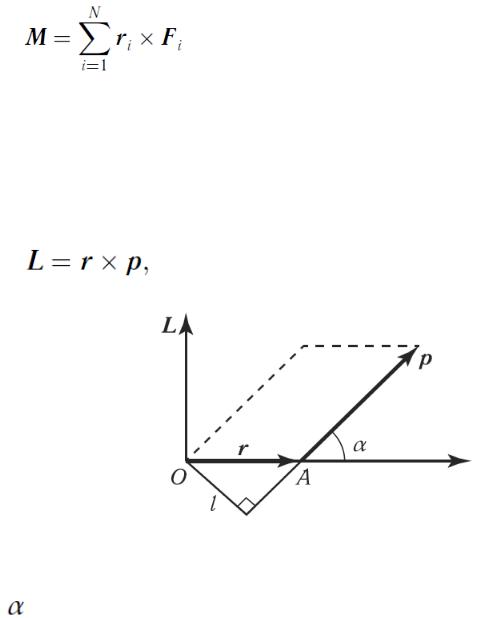
Моментом импульса материальной точки относительно точки О называется векторное произведение радиуса-вектора 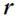 на
на
импульс 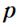 (рисунок 35):
(рисунок 35):
(88)
Рисунок 35.
- угол между векторами 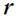 и
и 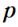 ; направление
; направление 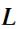 выбирается
выбирается
так, чтобы последовательность векторов 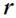 ,
, 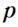 ,
,  образовывала правовинтовую систему.
образовывала правовинтовую систему.
Модуль момента импульса определяется как: L = r P sin α.
Для системы n материальных точек моментом импульса
относительно некоторой точки О называется векторная сумма моментов импульсов этих точек относительно того же начала:
67
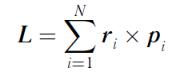
. |
(89) |
68
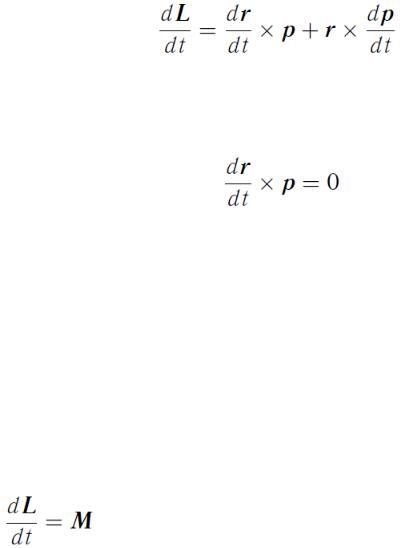
Закон сохранения моментов импульса
Предположим, что точка О неподвижна. В случае одной материальной точки, дифференцируя (88), получаем
.
При неподвижной точке О вектор 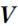 , равный
, равный 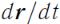 , параллелен
, параллелен 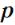 и поэтому
и поэтому
.
Мы знаем, что
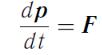 ,
,
и с учетом, что
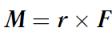 ,
,
получаем
, |
(90) |
- закон сохранения момента импульса для материальной точки.
Распространим его на систему материальных точек, для чего запишем уравнение (90) для каждой материальной точки
механической системы, понимая под 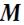 момент всех действующих на нее сил, как внутренних так и внешних.
момент всех действующих на нее сил, как внутренних так и внешних.
Внутренние силы входят в систему попарно так, что
69
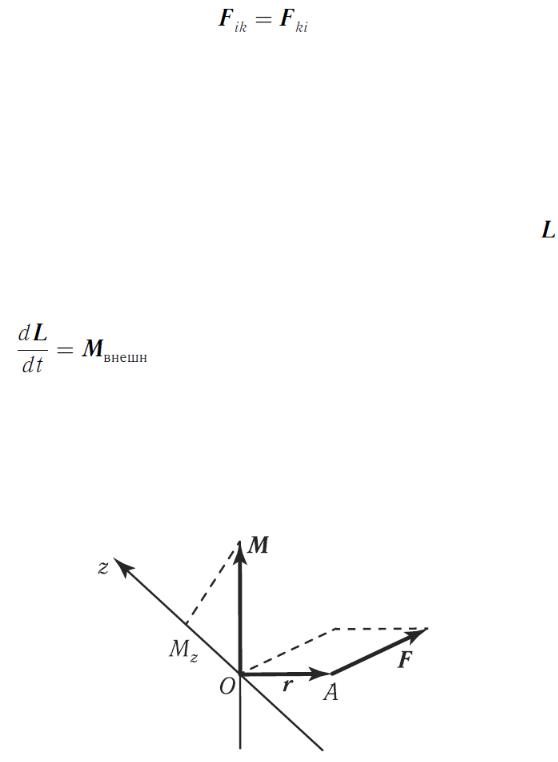
где 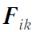 - сила воздействия k -й материальной точки на i -ю.
- сила воздействия k -й материальной точки на i -ю.
Кроме того, эти силы 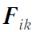 и
и 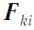 , действуют вдоль одной и той же прямой. Момент таких двух сил, а значит и моменты всех внутренних сил равны нулю.
, действуют вдоль одной и той же прямой. Момент таких двух сил, а значит и моменты всех внутренних сил равны нулю.
Для системы материальных точек, в котором момент импульса
определяется выражением (88), а момент силы 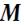 - выражением (86) для внешних сил, можно показать, что
- выражением (86) для внешних сил, можно показать, что
. |
(91) |
Моментом силы механической системы относительно оси
называется проекция на эту ось вектора момента силы системы относительно любой точки, выбранной на рассматриваемой оси (рисунок 36).
Рисунок 36.
Соответственно, моментом импульса относительно оси
называется проекция на эту ось вектора момента импульса относительно любой точки на данной оси.
70
