
glava01
.pdf
ГЛАВА 1
ЛИНЕЙНЫЕ СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ
1.1.СОБСТВЕННЫЕ КОЛЕБАНИЯ В КОНСЕРВАТИВНОЙ СИСТЕМЕ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ
Консервативная система – это идеализированная система, при анализе которой пренебрегают всеми возможными видами потерь энергии из системы. Подобная идеализация позволяет достаточно просто проанализировать важные свойства колебательных систем с малыми потерями.
Движение маятника, груза на пружине, заряда в электрическом контуре, эволюцию во времени многих систем в физике, химии, биологии и других науках при определенных предположениях можно описать одним и тем же ДУ, которое в теории колебаний выступает в качестве основной модели. Эта модель называется гармоническим осциллятором.
Для консервативных систем уравнение имеет вид
|
|
|
x =ƒ(x). |
|
|
(1.1) |
|
Точками сверху принято обозначать производные по времени: |
|||||||
|
dx |
= x, |
d 2 x |
= x, |
dq |
= q |
и т. д. |
|
dt |
dt2 |
dt |
||||
|
|
|
|
|
|||
Вмеханической системе x представляет смещение, в электрической системе это может быть, например, заряд.
При описании механических колебаний уравнение (1.1) выражает баланс силы инерции, отнесенной к единице массы, и возвращающей силы.
Вконкретных случаях, пренебрегая потерями, для колебаний математического маятника уравнение (1.1) имеет вид
x + |
g |
sin x = 0, |
(1.2) |
|
|||
|
l |
|
|
9 |
|
||
для груза на пружине:
x + |
k |
x = 0. |
(1.3) |
|
m |
||||
|
|
|
В случае электрического колебательного контура без потерь из закона Кирхгофа следует
q + |
1 |
q = 0. |
(1.4) |
|
LC |
||||
|
|
|
Уравнение (1.4) получено в предположении линейности элементов, образующих контур.
Рассмотрим еще один пример собственных колебаний – известную модель в биологии «хищник – жертва» [3].
Пусть на замкнутом пространстве живут два вида: хищники и вегетарианцы (жертвы). Число жертв – N1(t), а число хищников – N2 (t), где t –
время. Если жертвы живут одни и пищи достаточно, то их численность будет увеличиваться:
N |
= ε N , |
(1.5) |
|
1 |
1 |
1 |
|
где N1 – скорость роста числа жертв; ε1 > 0 – коэффициент прироста.
Если бы жили одни хищники, то из-за отсутствия пищи они бы вымерли:
N2 = −ε2 N2 , ε2 > 0, |
(1.6) |
где N2 – скорость уменьшения числа хищников; ε2 |
– коэффициент вы- |
мирания.
При совместном проживании численность хищников будет увеличиваться пропорционально N1N2 . Следовательно, для описания совместно-
го существования двух видов вместо соотношений (1.5), (1.6) следует записать:
N |
= ε N −γ |
2 |
N N |
, |
N |
2 |
= −ε |
N |
2 |
+ γ N N |
, |
γ > 0, γ |
2 |
> 0, (1.7) |
||||
1 |
1 |
1 |
1 |
2 |
|
|
2 |
|
1 |
1 |
2 |
|
1 |
|
||||
где γ1 – коэффициент пропорциональности, характеризующий размножение хищников; γ2 – коэффициент пропорциональности, характеризующий гибель жертв в результате встречи с хищниками.
Для состояния равновесия, когда |
N |
|
= 0, |
N |
2 |
= 0, |
|
|||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
||
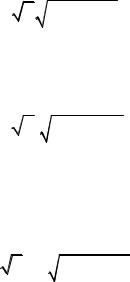
N = N |
= |
ε2 |
, |
N |
2 |
= N |
20 |
= |
|
ε1 |
. |
(1.8) |
||
|
|
|||||||||||||
1 |
10 |
|
γ |
|
|
|
|
|
γ |
2 |
|
|
||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
10
При малых отклонениях численности от состояния равновесия можно записать:
N1 (t )= N10 + n1 (t ), N2 (t )= N20 + n2 (t ). |
(1.9) |
Подставляя (1.9) в (1.7) и пренебрегая нелинейными слагаемыми, получаем
dn1 |
=− |
γ2ε2 |
n , |
dn2 |
= |
γ1ε1 |
n . |
(1.10) |
|
dt |
γ |
dt |
|
||||||
|
2 |
|
γ |
1 |
|
||||
|
|
1 |
|
|
|
|
2 |
|
|
Уравнения (1.10) можно свести к одному для n1 или n2 , аналогичному соотношению (1.1):
d 2n |
|
|
|
|
|
1,2 |
+ε ε n |
= 0. |
(1.11) |
||
|
|||||
dt2 |
1 |
2 |
1,2 |
|
|
|
|
|
|
|
|
Итак, из рассмотренных примеров очевидно, что в общем виде уравнение колебаний в консервативной системе соответствует (1.1). Сделав под-
становку y = dxdt , проинтегрируем (1.1). Интеграл уравнения примет вид
y2 |
= ∫ f (x)dx + h. |
(1.12) |
|
2 |
|||
|
|
Левая часть выражения (1.12) может трактоваться как кинетическая энергия единичной массы. Интеграл в правой части выражает работу силы f (x) на некотором участке изменения координаты x и может быть истол-
кован как функция, описывающая потенциальную энергию системы. Тогда постоянная интегрирования h выражает полный запас энергии в системе.
Введя обозначение W (x)= −∫ f (x)dx, получим
y = ± 2 h −W (x). |
(1.13) |
Поскольку y = dxdt , то
dt = ± |
1 |
|
dx |
. |
2 |
|
h −W (x) |
||
|
|
|
Если при определении периода колебаний T принять, что моментам времени 0 и T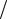 2 соответствуют амплитудные значения x1 = −A,
2 соответствуют амплитудные значения x1 = −A,
x2 = +A, то
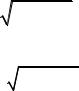
T = 2 |
1 |
A |
dx |
. |
(1.14) |
|
|
∫ |
|
||||
2 |
h −W (x) |
|||||
|
−A |
|
|
11
Анализируя соотношение (1.14), можно сделать вывод, что в нелинейной системе период колебаний зависит от амплитуды колебаний. Такие колебания называются неизохронными, а системы, в которых наблюдаются подобные колебания, – неизохронными системами.
Для линейной системы уравнение (1.1) примет вид
|
|
|
|
|
|
d 2 x = −ω2 x. |
|
|
|
|
|
|
|
|
(1.15) |
|||||||||||
|
|
|
|
|
|
dt2 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
В уравнении (1.2) sin x ≈ x, |
ω2 |
= |
g |
|
, |
в (1.3) ω2 |
= |
k |
, в (1.4) |
ω2 |
= |
|
1 |
, в |
||||||||||||
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
0 |
|
l |
|
|
|
|
|
|
|
|
0 |
|
m |
|
0 |
|
LC |
||||
(1.11) ω2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
= ε ε |
2 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В рассматриваемом случае |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
W (x)= |
1 |
ω2 x2 , |
|
|
|
y2 |
= h − ω02 x2 . |
|
|
|
|
|
|
||||||||||
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|||
Значение h можно определить из условия, что скорость |
y = 0, |
если |
||||||||||||||||||||||||
координата x = ±A, тогда y =ω |
A2 |
|
− x2 и |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T = |
2 |
|
A |
|
|
dx |
|
|
= |
2π |
. |
|
|
|
|
|
(1.16) |
||||||
|
|
|
|
|
∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
ω |
|
A |
2 |
|
− x |
2 |
ω |
|
|
|
|
|
|||||||||||
|
|
|
|
0 −A |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|||||||
Следовательно, период колебаний в линейной консервативной системе, определяемый соотношением (1.16), не зависит от амплитуды колебаний. Подобную систему называют изохронной, а колебания – изохронными.
1.2. МЕТОД ФАЗОВОЙ ПЛОСКОСТИ ПРИ АНАЛИЗЕ ДИНАМИЧЕСКИХ СИСТЕМ
Уравнение гармонического осциллятора позволяет найти его состояние в любой момент времени, если известны величины, описывающие состояние в некоторый начальный момент времени. Согласно этому свойству, осциллятор принадлежит к классу динамических систем. Дадим одно из определений понятия «динамическая система». «Динамическая система – математический объект, соответствующий реальным физическим (химическим, биологическим и др.) системам, эволюция которых на бесконечном интервале времени однозначно определяется начальным состоянием. Можно сказать, что реальному процессу соответствует динамическая система, если этот процесс удается описать с помощью системы уравнений, допускающих существование на беско-
12
нечном интервале времени единственного решения для любого начального условия» [3]. Под состоянием системы в момент времени t понимают значения величин, количества которых достаточно для определения этих величин в последующие моменты времени. Такие величины называют динамическими переменными. Для осциллятора, например, состояние системы однозначно определено заданием его координаты и скорости.
Множество всех возможных состояний системы называется фазовым пространством. Размерность фазового пространства совпадает с числом динамических переменных.
Рассматриваемый нами гармонический осциллятор – динамическая система с размерностью фазового пространства, равной 2. В качестве ди-
намических переменных выступают координата x и скорость y = dxdt .
В общем виде уравнение (1.15) для системы с одной степенью свободы можно записать как
d 2 x |
= |
|
dx |
|
(1.17) |
dt2 |
f x, |
dt |
. |
||
|
|
|
|
Как будет показано в дальнейшем, уравнение (1.17) описывает колебания в системах, в которых есть трение.
Проведя замену переменных y = dxdt , получим
dy = |
f (x, y) |
. |
(1.18) |
|||||||
|
|
|||||||||
dx |
y |
|
|
|
|
|
|
|
||
Решение уравнения (1.18) можно |
|
|
|
y |
|
|
|
|
||
|
|
|
|
|||||||
изобразить в виде графика y = y(x) |
|
|
|
|
|
|
|
xi , yi |
||
на плоскости с координатами x и y, |
|
|
|
|
|
|
|
|||
которая и является фазовой плоско- |
|
|
|
|
|
|
|
|
|
|
стью (рис. 1.1). |
|
|
|
|
|
|
|
|
|
|
Точки с координатами xi , yi , ото- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|||
бражающие состояние системы в мо- |
|
|
|
|
|
|
|
|
|
|
мент времени ti , называют изобра- |
|
|
|
|
|
|
|
|
|
|
жающими точками. А решения y = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
= y(x), представляющие собой сле- |
|
|
|
|
|
|
|
|
|
|
ды перемещения изображающих то- |
|
|
|
Рис. 1.1. Общий вид фазовой |
||||||
чек на фазовой плоскости, называют |
|
|
|
|||||||
|
|
траектории для консервативной |
||||||||
фазовыми траекториями. Величина |
системы с одной степенью свободы |
|||||||||
13

dydx в (1.18) есть угловой коэффициент касательной к некоторой фазовой
траектории в заданной точке с координатами xi и yi .
Рассмотрим общие свойства фазовых траекторий. При изменении динамического состояния системы изображающие точки перемещаются по плоскости XY следующим образом: в верхней полуплоскости слева направо, в нижней – справа налево.
Это следует из того, что в верхней полуплоскости dx = ydt > 0
(x возрастает), а в нижней − dx < 0 (x убывает).
В точках пересечения фазовых траекторий с осью x f (x, y)= f (x, 0). Если при этом f (x, 0)≠ 0, то
dydx = f (x0, 0) →∞.
Следовательно, касательная к фазовой траектории в точке пересечения оси x перпендикулярна оси x. Фазовые траектории пересекают ось x только под прямым углом. Если f (x, 0)= 0, то dydx = 00 . Точки, в которых выполняется данное условие, называются особыми точками. Для особых точек характерно равенство нулю кинетической энергии системы, поскольку y = 0. Функция, описывающая потенциальную энергию, имеет экстремум, так как f (x, 0)= 0 и, значит, dWdx
точки соответствуют положениям равновесия динамической системы. Из единственности решения дифференциального уравнения следует
утверждение, что через каждую неособую точку на фазовой плоскости проходит одна и только одна фазовая траектория. В особых точках условия существования и единственности решения нарушаются. Через особую точку может проходить произвольное число фазовых траекторий либо не проходить ни одной, т. е. особая точка представляет собой отдельную траекторию.
Для консервативных систем уравнение фазовых траекторий имеет вид (1.13). Значения функции y расположены на фазовой плоскости симметрично оси x. Эта симметричность является признаком консервативной системы.
Семейства интегральных кривых образуют фазовый портрет, который состоит из фазовых траекторий и особых точек. Замкнутым фазовым траекториям на фазовом портрете соответствуют периодические колебательные процессы.
14
1.3.ФАЗОВЫЙ ПОРТРЕТ КОНСЕРВАТИВНОЙ СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ
Используя соотношение (1.13), запишем уравнение фазовых траекторий для консервативных систем:
y2 |
= h −W (x). |
(1.19) |
|
2 |
|||
|
|
При известном значении W(x) легко найти особые точки xi, соответствующие положению равновесия.
Рассматривая малые отклонения x и y от равновесных положений xi, yi = 0, можно получить фазовые траектории в окрестности особых точек.
Пусть x = xi +ξ, y = yi +η. Разложим W(x) |
в ряд: |
|
|
|
||||||||||
W (x + ξ) =W (x ) + dW / dx |
|
x=x |
ξ + (1/ 2)d 2W / dx2 |
|
|
x=x |
ξ2 |
+... . |
||||||
|
|
|||||||||||||
i |
|
i |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
i |
|
|
|
|
|
|
i |
|
|
Обозначим |
W (x ) = h , |
d 2W / dx2 | |
x=x |
= α. |
Учтем, |
что y = 0 + η, |
||||||||
|
i |
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
dW/dx│x=xi = 0. Тогда из уравнения (1.19) |
|
|
|
|
|
|
|
|||||||
|
|
η2 / 2 = h – hi – 1 / 2 αξ2 |
|
|
|
|||||||||
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
η2+ αξ2 = H, |
|
|
|
|
|
(1.20) |
|||||
где H = 2(h − hi).
Если α > 0, то выражение (1.20) описывает семейство эллипсов. Если
α< 0, это семейство гипербол. Знак α определяет вид особых точек. Особая точка, для которой α > 0, называется центром. Фазовые траек-
тории в малой окрестности центра – эллипсы. Особая точка центр соответствует минимуму потенциальной энергии ( α = d2W/dx2│x=xi ), т. е. устойчивому состоянию динамической системы. Особая точка, для которой
α< 0, называется седлом. Она соответствует неустойчивому состоянию системы (максимуму потенциальной энергии).
Используя сведения об особых точках и фазовых траекториях, можно построить фазовый портрет консервативной системы как совокупность семейства фазовых траекторий и особых точек. К этим двум основным элементам фазового портрета следует добавить фазовые траектории, пограничные между областями фазовой плоскости с движениями различного характера. Эти траектории носят название разделительных линий или сепаратрис. Их расположение наглядно показывает области возможных движений разного типа и те значения координат x, y, при которых одно движение переходит в другое.
15
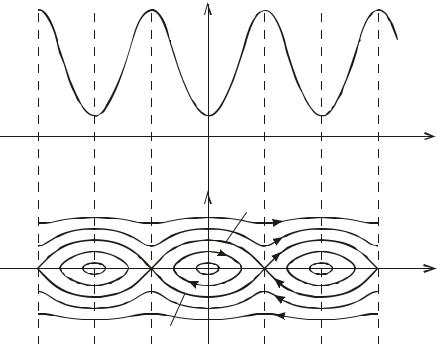
Рассмотрим примеры, иллюстрирующие построение фазовых портретов. Построим фазовый портрет колебаний математического маятника, поведение которого определяется соотношением (1.2). Сравнивая (1.1) и (1.2), находим f (x) = −g / l·sin x. Соответственно, с точностью до постоян-
ной, W(x) = − ω02 cos x. А уравнение фазовых траекторий будет иметь вид
y2 / 2 − ω2 cos x = h. |
(1.21) |
0 |
|
Используя (1.21) и выражение для потенциальной энергии, легко найти особые точки и построить фазовые траектории (рис. 1.2). Замкнутые траектории, окружающие особые точки типа центр с координатами y = 0, x = 2πn (n − любое целое число), характеризуют колебательные движения маятника вокруг устойчивого равновесия, соответствующего минимуму потенциальной энергии. Особые точки y = 0, x = (2n – 1)π типа седло соответствуют верхнему положению равновесия – максимуму потенциальной энергии.
Кривые 1 и 2 являются сепаратрисами. Они разделяют различные области на фазовой плоскости: область замкнутых траекторий и область приходящих из −∞(+∞) и уходящих в +∞(−∞). Эти траектории соответ-
ствуют вращательным движениям маятника. |
|
W(x) |
|
|
x |
y |
1 |
|
|
|
x |
2 |
|
Рис. 1.2. Фазовый портрет маятника |
|
16

Для электрического колебательного контура, описываемого уравне-
|
|
|
|
|
|
|
d 2 x |
|
нием (1.4), на основании (1.1) получим |
dt2 = −ω2 x , где x = q, ω2 = 1/LC. |
|||||||
Следовательно, уравнение фазовых траекторий |
||||||||
|
y2 |
2 |
x2 |
|
|
dx |
||
|
|
+ ω |
|
= h , |
|
y = dt , |
||
|
2 |
|
2 |
|
||||
где h − постоянная интегрирования. |
|
|
|
|||||
|
|
|
|
1 |
2 |
2 |
|
|
Потенциальная энергия W (x) = 2 |
ω x |
|
, а особая точка для рассматри- |
|||||
ваемого процесса x = 0 – точка типа центр. Фазовые траектории, описывающие поведение системы, − эллипсы.
Рассмотрим теперь фазовый портрет системы «хищник − жертва».
В качестве динамических переменных для описания системы можно взять численности популяций жертв N1 и хищников N2. Если же принять
за координаты x = N1, y = dNdt1 или x = N2, y = dNdt2 , то анализ будет тождествен случаю колебательного контура (как следует из уравнения (1.11)), но не будет полным, так как взаимосвязь в системе «хищник – жертва» на такой фазовой плоскости не будет отражена. Фазовым пространством в этом случае будет четверть плоскости, поскольку N1 ≥ 0,
N2 ≥ 0.
Введем в рассмотрение фазовую плоскость с безразмерными координатами x = N1/N10 и y = N2/N20, где N10 и N20 определяются соотноше-
нием (1.8). Тогда уравнения (1.7) можно привести к виду |
|
||||||
dx = −ε x(y −1), |
dy =ε |
2 |
y(x −1) |
|
|||
dt |
1 |
|
dt |
|
|
|
|
|
|
|
|
|
|
||
или, разделив одно на другое, |
y(x −1) |
|
|
|
|
|
|
dy |
= − |
, α = |
ε1 |
. |
(1.22) |
||
dx |
αx(y −1) |
|
|||||
|
|
|
ε2 |
|
|||
Проинтегрировав (1.22), получим |
|
|
|
|
|
||
(x −ln x)+α(y −ln y)= c, |
(1.23) |
||||||
где с − постоянная интегрирования.
Значения x = 1, y = 1 соответствуют точке равновесия системы. Для малых отклонений от точки равновесия x = 1 +ξ, y = 1 +η
ln (1 + ξ)≈ ξ − ξ2 / 2, ln (1 + η)≈ η− η2 / 2.
17
y |
|
1 |
|
0 |
1 |
|
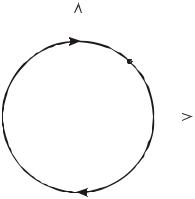
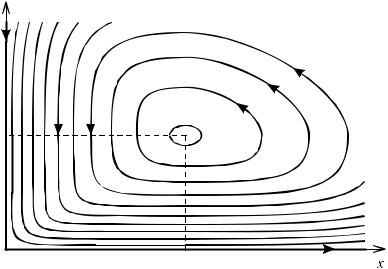
Рис. 1.3. Фазовый портрет системы «хищник − жертва» |
Таким образом, вблизи особой точки уравнение (1.23) для фазовой траектории приобретает вид
ξ2 +αη2 = 2c.
Поскольку α > 0, то фазовые траектории являются вложенными друг в друга эллипсами, а особая точка − центр.
Очевидно, что система «хищник – жертва» имеет еще одну особую точку – это положение равновесия N1 = 0, N2 = 0, т. е. x = 0, y = 0.
Анализ показывает [3], что данная особая точка представляет собой точку типа седло, а траектории, входящие и выходящие из седла, являются сепаратисами. В целом вид фазового портрета показан на рис. 1.3.
1.4.ФАЗОВЫЙ ПОРТРЕТ ДИССИПАТИВНОЙ СИСТЕМЫ
СОДНОЙ СТЕПЕНЬЮ СВОБОДЫ
В общем случае уравнение колебаний в нелинейной диссипативной системе с одной степенью свободы имеет вид
d 2 x |
= |
|
dx |
(1.24) |
dt2 |
f x, |
. |
||
|
|
dt |
|
Для линейного гармонического осциллятора выражение (1.24) записывается как
d 2 x |
+ 2δ dx |
+ ω02 x = 0. |
(1.25) |
dt 2 |
dt |
|
|
18
