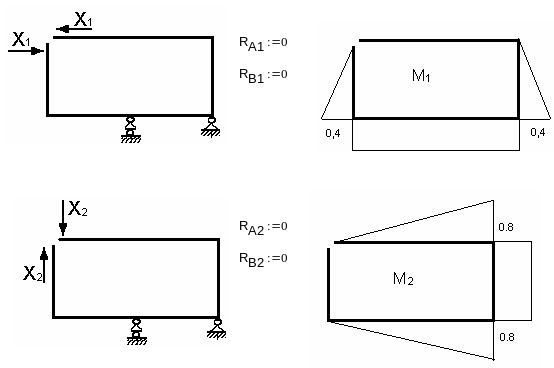
- •Построение диаграмм внутренних сил nр, tр, m р от заданной нагрузки.
- •Часть стержня искривлённая по дуге окружности.
- •2. Построение диаграммы изгибающих моментов .
- •Определение перемещения сечения а по интегралам Мора.
- •Рассчитаем коэффициента в каноническом уравнении
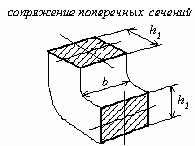
- •3. Подбор размеров поперечных сечений по условию прочности.
Определение перемещения сечения а по интегралам Мора.
В системах, элементы которых сопротивляются изгибу, энергия нормальных сил и энергия поперечных сил малы по сравнению с энергией от изгиба и все перемещения вызываемые растяжением и сдвигом несущественны в сравнении с перемещениями от изгиба. Поэтому во вспомогательном состоянии не определялись нормальные и поперечные силы и из трёх интегралов Мора (для плоской системы) берём один, учитывая только энергию изгибающих моментов:
![]() .
.
Интегрирование
производится по длине участков (частей)
![]() и затем осуществляется суммирование
интегралов.
и затем осуществляется суммирование
интегралов.
В нашем случае имеется три участка: горизонтальная часть стержня, вертикальная и часть стержня изогнутая по дуге окружности:
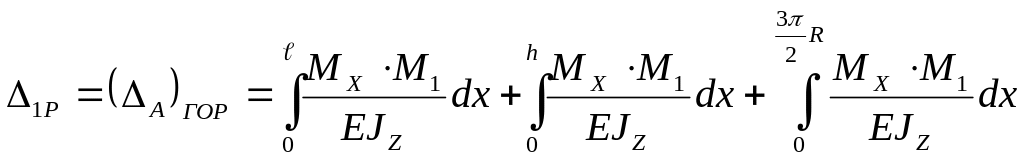 .
.
Вычисляем последовательно интегралы:
![]()
![]() .
.
![]()
Для
проверки эти интегралы вычислим
графоаналитическим способом Верещагина,
который применим только для прямых
участков с постоянными в пределах
каждого участка поперечными сечениями.
Интегрирование заменяется умножением
площадей
![]() диаграммы грузового состояния
диаграммы грузового состояния
![]() на ординаты диаграммы вспомогательного
состояния
на ординаты диаграммы вспомогательного
состояния
![]() под центрами тяжести площадей
:
под центрами тяжести площадей
:
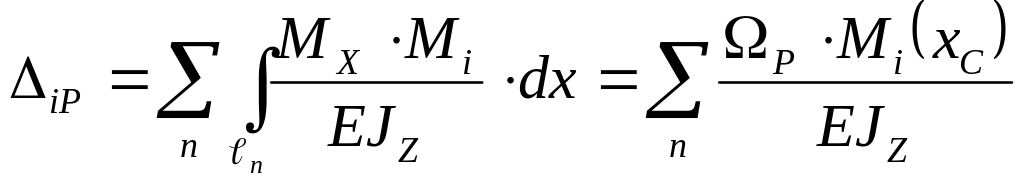 .
.
Рассмотрим участок I для этого построим отдельно диаграммы от распределённой нагрузки, и от реакции RA
От RA
![]()
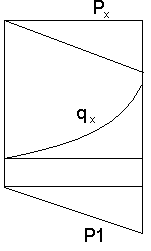 От qx
От qx
![]()
6,74 От
![]()
![]()
4,48
![]()
![]()
![]()
0,246
![]()
![]()
Рассмотрим участок II
 Изгибающий момент от силы P
равен
Изгибающий момент от силы P
равен
![]()
Изгибающий момент от силы P1 равен
![]()
![]()
0,88 0,4
![]()
![]()
Рассчитаем перемещение на криволинейном участке
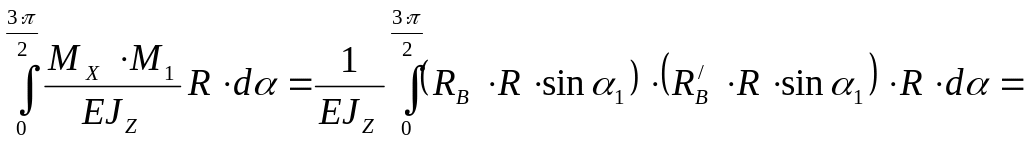
![]()
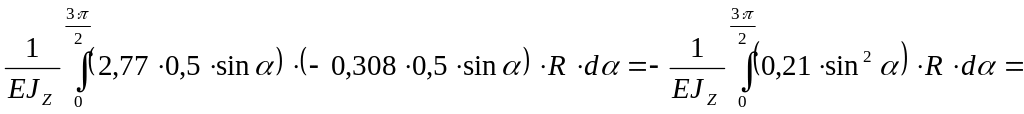
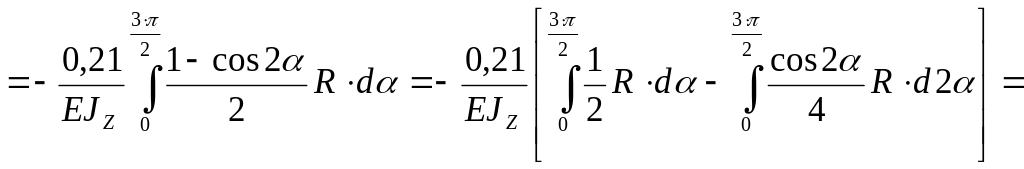
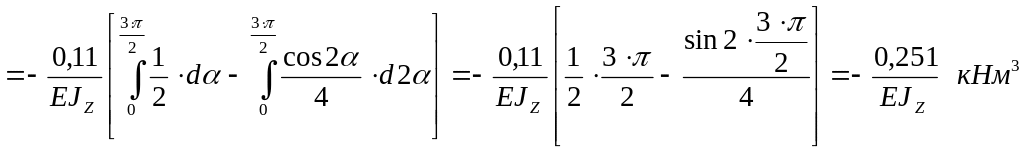
Рассчитаем горизонтальное перемещение сечения А как сумму перемещений на всех участках рамы
![]() .
.
Определить размеры поперечного сечения стержня из условия ограничивающего перемещение сечения А (условия жёсткости):
![]() .
.
Определяем требуемый осевой момент инерции сечения:
![]() .
.
Этот момент инерции можно обеспечить при любой форме поперечного сечения.
О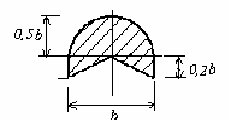 пределим
необходимые размеры заданной
формы сечения.
пределим
необходимые размеры заданной
формы сечения.
Сечение имеет
одну ось симметрии
![]() .
Эта ось главная и центральная. Изгиб
происходит относительно другой главной
оси Z, проходящей через
центр тяжести сечения, положение которого
неизвестно и его необходимо определить.
.
Эта ось главная и центральная. Изгиб
происходит относительно другой главной
оси Z, проходящей через
центр тяжести сечения, положение которого
неизвестно и его необходимо определить.
Найдём
положение центра тяжести сечения
относительно вспомогательной оси
![]() ,
разделив его на составляющие элементы
- прямоугольник и полукруг:
,
разделив его на составляющие элементы
- прямоугольник и полукруг:
![]() .
.
Момент инерции всего сечения относительно главной оси:
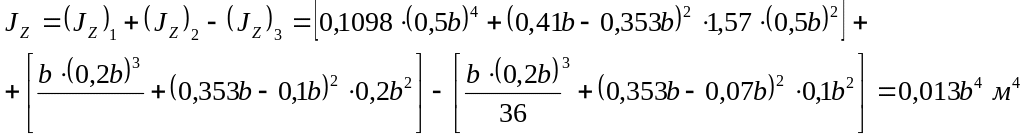
Определяющий размер сечения должен быть:
![]() .
Принимаем
.
Принимаем
![]()
При этом перемещение сечения А:
![]() .
.
Максимальные напряжения от изгиба:
![]() .
.
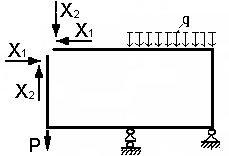
С х е м а 2 (изображать в масштабе по заданным размерам).
Дано: Р = 2,2 кН, q = 14 kH/м, h = 0,4 м, = 0,8 м,.
М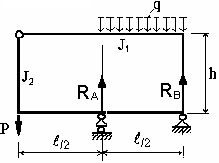 атериал:
Сталь Ст.3,
,
атериал:
Сталь Ст.3,
,
![]() .
.
Определяем опорные реакции.
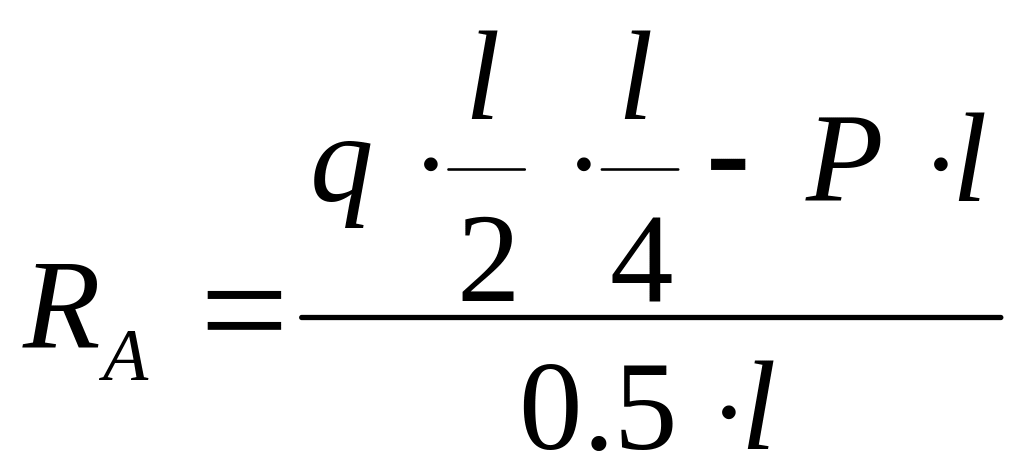
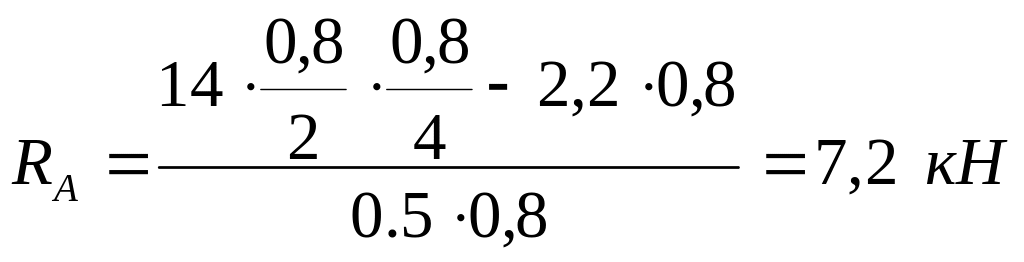
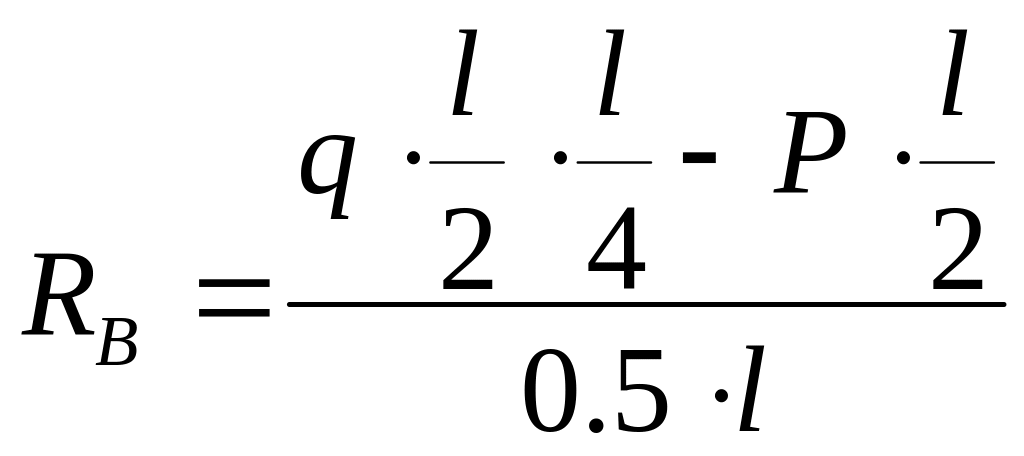
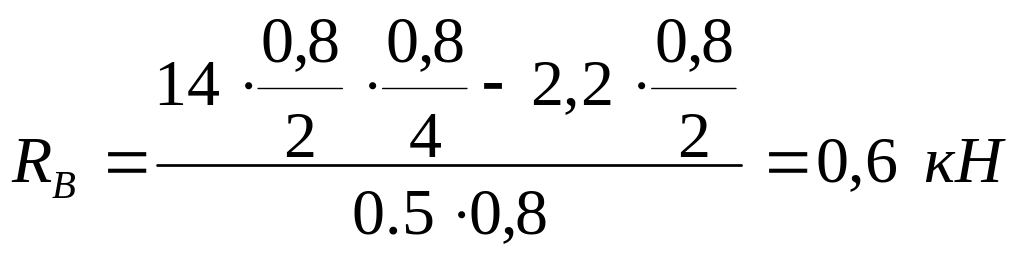
Проверка:
![]()
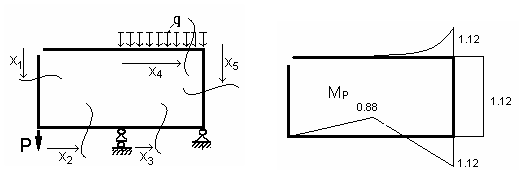
Разрываем связь в шарнире и составляем канонические уравнения
![]() ,
,
![]()
Определяем коэффициенты в канонических уравнениях .
MX1=0
При X2=0
![]()
При X2=l/2
![]()
При X3=0
![]()
При X3=l/2
![]()
При X4=0
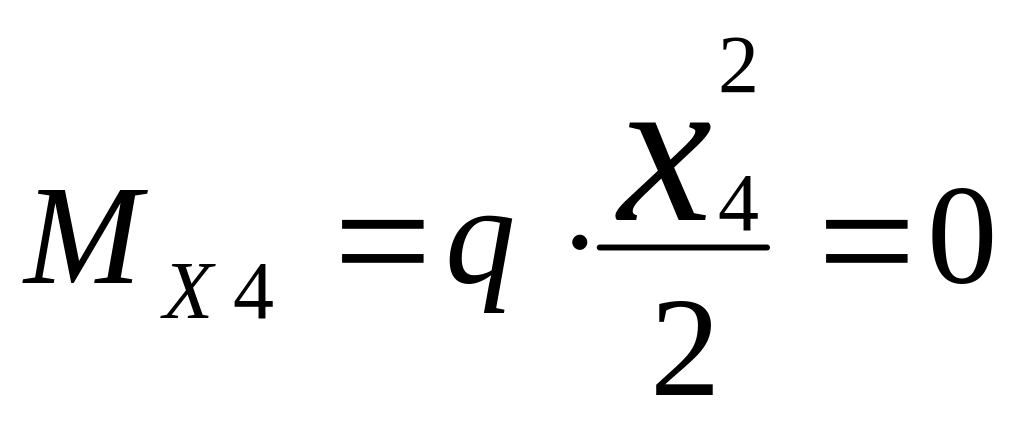
При X4=l/2
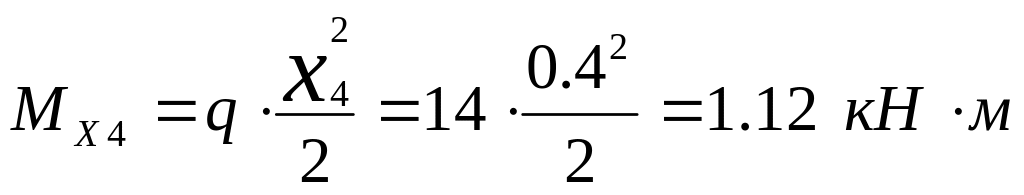
При X5=0
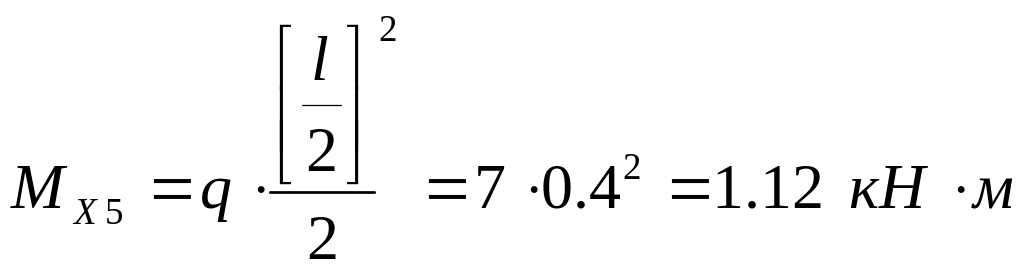
При X5=l