§ 11.2. Тригонометрические и показательные функции
1. Рассматриваются
интегралы
,
где
дробно-рациональная функция, двух
аргументов
и
.
Другими словами, в числителе и знаменателе
этой дроби присутствуют только целые,
положительные степени этих аргументов.
Заменой переменной
эти интегралы сводятся к интегралам
,
причем
дробно-рациональная функция, но уже
аргумента
,
что приводит поставленную задачу к
задаче предыдущего параграфа.
Этот переход может
быть осуществлен с помощью, так называемой,
универсальной подстановки
.
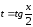Покажем, что функции
и
,
а также
оказываются рациональными функциями
новой переменной
.
,
.
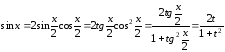При получении
первой формулы учитывалось, что
.
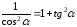Кроме того, из
следует
.
Итак,
.
Указанная подстановка позволяет свести рассматриваемый интеграл к интегралу предыдущего класса при любой дробно-рациональной функции R . Однако, как показывает опыт, эта замена чаще всего приводит к сложным интегралам от рациональных дробей, их интегрирование весьма затруднительно, а иногда невозможно.
В некоторых случаях с помощью других подстановок удается получить более простые дробно-рациональные функции. В отличие от универсальной, эти подстановки, называют иногда специальными, так как применимы они лишь при выполнении некоторых условий.
1. Замена применима при выполнении условия
,
то есть подынтегральная
функция нечетна относительно
.
Докажем это.
Упомянутое условие, очевидно, реализуется
в двух случаях: а) когда в числителе
рациональной функции присутствует
только нечетные степени
,
а в знаменателе – только четные, б) в
числителе имеются только четные степени
,
а в знаменателе – только нечетные.
Очевидно, случай б) сводится к случаю
а) умножением числителя и знаменателя
дроби на
.
Следовательно, достаточно рассмотреть
случай а). Вынесем за скобку
,
тогда и в числителе, и в знаменателе
рациональной функции будут только
четные степени
что позволяет сделать следующие
преобразования
,
что и требовалось доказать.
2. Замена
применима при выполнении условия
,
то есть в случае,
когда подынтегральная функция нечетна
относительно
.
Доказательство аналогично.
3. Замена
применима при выполнении условия
.
Это условие
реализуется, когда функция
либо четна, либо
нечетна одновременно относительно
и
.
Первый из этих вариантов очевиден,
второй сводится к первому. В самом деле,
если функция нечетна относительно
и
,
то
.
Итак,
откуда следует
,
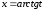тогда
,
,
.
В результате
.
Таким образом, приведение рассматриваемого класса интегралов к предыдущему классу возможно двумя способами. Либо применение универсальной подстановки, приводящей почти всегда к интегрированию сложных дробно-рациональных функций, либо использование, когда это возможно, наиболее подходящей специальной подстановки.
Применение универсальной подстановки целесообразно, когда не работает ни одна из специальных подстановок.
Если допустимы несколько специальных подстановок, желательно осуществить каждую из них, чтобы выбрать ту, которая приводит к интегрированию самой простой рациональной дроби.
Пример 1. Вычислить
.
Нетрудно проверить,
что можно реализовать все приведенные
выше подстановки. В самом деле,
подынтегральная функция нечетна и
относительно
,
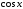и относительно
,
одновременная смена знака перед этими
функциями не изменяет подынтегральной
функции, универсальная подстановка
осуществима в этих интегралах всегда.
Реализуем поочередно все подстановки.
А) универсальная подстановка
.
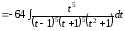В результате имеем правильную, несократимую дробь. Ее можно представить в виде суммы одиннадцати простейших дробей. Относительно коэффициентов разложения получается система 12 алгебраических уравнений.
В) Замена
:
.
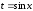Подынтегральная функция может быть представлена в виде суммы шести простейших дробей, для отыскания коэффициентов разложения требуется решить систему 6 алгебраических уравнений. Задача значительно проще по сравнению с A).
С) Замена
:
.
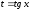Итак, необходимо вычислить интеграл от неправильной дробно-рациональной функции, что значительно проще вычисления интеграла B), не говоря уж об A).
D)
Замена
:
.
Таким образом, последний вариант замены переменной оказался самым удачным, с помощью этой подстановки интеграл был вычислен. В ходе решения подтвердилось, что универсальная подстановка в рассмотренном примере приводит к значительно более трудоемким вычислениям.
Пример 2. Вычислить
.
В этом случае не работает ни одна из
специальных подстановок, приходится
применять универсальную
.
Знаменатель подынтегральной функции имеет действительные корни, следовательно, она может быть представлена в виде суммы двух простых дробей
,
откуда следует система уравнений
,
решение которой
.
Итак,
.
Интегралы вида
рассмотрим отдельно. Вообще говоря, эти
интегралы являются частным случаем
интеграла
,
следовательно, к ним применима
вышеизложенная теория. Ее следует
использовать, когда один из показателей
степени нечетен. Если
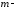нечетно,
то делается замена
,
если нечетно
,
реализуется замена
.
Интересен случай,
когда
и
четны. Теория предлагает в этом случае
замену
.
Однако удобнее использовать одну из
формул
.
Введение двойного угла позволяет понизить общую степень подынтегральной функции, что, конечно, упрощает вычисление интеграла.
Пример 3.
.
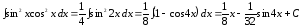Наконец, интегралы
вида
,
,
преобразуются с помощью формул
,
,
.
Примеры для самостоятельного решения
Вычислить интегралы
11.6.
,
11.7.
,
11.8.
,
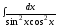11.9.
,
11.10.
,
11.11.
,
11.12.
,
11.13.
,
11.14.
.
Показательные функции
Вычисляются
интегралы вида
,
где
дробно-рациональная функция аргумента
.
В этом классе рекомендуется замена
,
тогда
.
Пример.
Примеры для самостоятельного решения
11.15.
,
11.16.
,
11.17.
.