
Формула Эйлера
При рассмотрении
комплексных чисел использовалась без
доказательства формула Эйлера
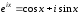 .
Теперь появилась возможность ее доказать.
Используем разложение функции
.
Теперь появилась возможность ее доказать.
Используем разложение функции
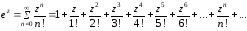 .
.
Примем
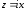 (в разложении использована договоренность,
что
(в разложении использована договоренность,
что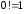 ).
Тогда
).
Тогда
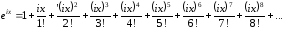 .
.
Если учесть, что
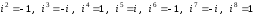 и т.д., то
и т.д., то
 ,
,
Сравнивая полученное выражение с разложениями
 ,
,
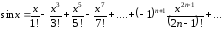 ,
,
нетрудно убедиться, что формула Эйлера справедлива.
Ряды Фурье
Наряду со степенными рядами к наиболее распространенным функциональным рядам относятся ряды Фурье.
Классический ряд Фурье – это ряд вида
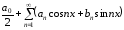 ,
,
где
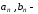 постоянные
коэффициенты. Таким образом, ряды Фурье
- тригонометрические, а их сумма -
периодическая функция с периодом
постоянные
коэффициенты. Таким образом, ряды Фурье
- тригонометрические, а их сумма -
периодическая функция с периодом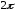 .
.
Данное обстоятельство
существенно ограничивает область
применимости рядов Фурье, так как далеко
не всякий реально происходящий процесс
является периодическим, да еще с периодом
 .
Поэтому основные усилия математиков
были направлены на смягчение указанных
ограничений путем внесения некоторых
дополнительных условий, о чем будет
сказано ниже.
.
Поэтому основные усилия математиков
были направлены на смягчение указанных
ограничений путем внесения некоторых
дополнительных условий, о чем будет
сказано ниже.
Рассмотрим систему функций, входящих в ряд Фурье
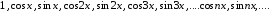
Эта система функций обладает двумя важнейшими свойствами - ортогональностью и полнотой.
Определение 1.
Систему функций
 называют ортогональной на некотором
промежутке
называют ортогональной на некотором
промежутке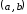 ,
если выполняются условия:
,
если выполняются условия:
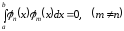 ,
,
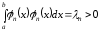 .
.
Когда
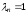 ,
система называется нормальной.
,
система называется нормальной.
Покажем, что система функций
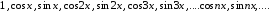
является ортогональной
системой на интервале
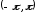 .
Для этого вычислим несколько интегралов
.
Для этого вычислим несколько интегралов
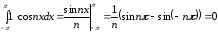 ,
,
 ,
,
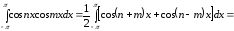
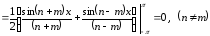 ,
,
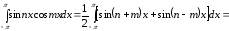
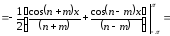
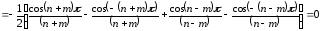 ,
,
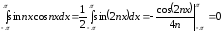 ,
,
 ,
, 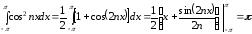 ,
,
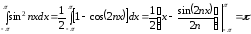 .
.
Итак, доказано,
что интегралы от произведений разных
функций этой системы равны нулю, интегралы
от произведений одинаковых функций
равны
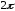 и
и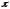 .
Ортогональность системы функций
доказана.
.
Ортогональность системы функций
доказана.
Определение 2. Система функций является полной в заданном промежутке, если нет ни одной, не входящей в эту систему, функции, кроме функции, тождественно равной нулю, ортогональной функциям системы.
Например, система
косинусов
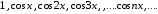 не обладает полнотой, так как любой
не обладает полнотой, так как любой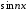 ортогонален и к 1, и ко всем функциям
ортогонален и к 1, и ко всем функциям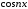 .
Следствием этого является то, что в ряды
по косинусам можно разлагать не все, а
только четные функции. По той же причине
не обладает полнотой и система синусов
.
Следствием этого является то, что в ряды
по косинусам можно разлагать не все, а
только четные функции. По той же причине
не обладает полнотой и система синусов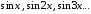 ,
что позволяет разлагать в ряд Фурье по
синусам только нечетные функции.
Доказательство полноты достаточно
сложно, поэтому ограничимся утверждением,
что вышеприведенная система
тригонометрических функций полна.
,
что позволяет разлагать в ряд Фурье по
синусам только нечетные функции.
Доказательство полноты достаточно
сложно, поэтому ограничимся утверждением,
что вышеприведенная система
тригонометрических функций полна.
Полнота системы функций обеспечивает единственность разложения в ряд Фурье (представления в виде ряда Фурье) любой, удовлетворяющей некоторым условиям, функции, что весьма ценно при решении с помощью рядов Фурье всевозможных уравнений.
Определение 3. Если функция в некоторой области имеет конечное число точек разрыва первого рода (конечные разрывы), а между этими точками она непрерывна, такая функция называется кусочно-непрерывной.
Определение 4. Если в некоторой области функция имеет конечное число точек, между которыми она дифференцируема, а в самих этих точках существуют конечные значения левых и правых пределов, как самой функции, так и ее производной, то она называется кусочно-дифференцируемой в этой области.
Теорема.
Для любой кусочно-дифференцируемой,
периодической с периодом
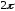 функции
функции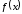 ее ряд Фурье сходится, а его сумма равна
ее ряд Фурье сходится, а его сумма равна

 ,
,
здесь
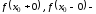 правый
и левый пределы функции
правый
и левый пределы функции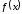 при
при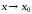 (теорема приводится без доказательства).
(теорема приводится без доказательства).
Следствие.
Сумма ряда равна
 ,
если функция непрерывна.
,
если функция непрерывна.
Известно, что ряд
Фурье, представляющий разложение
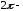 периодической
непрерывной функции, сходится равномерно.
периодической
непрерывной функции, сходится равномерно.
Разложение в ряд
Фурье
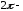 периодической
функции
периодической
функции
Теорема. Если
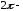 периодическая
функция
периодическая
функция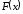 непрерывна (или кусочно-непрерывна), то
значение интеграла
непрерывна (или кусочно-непрерывна), то
значение интеграла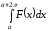 не зависит от
не зависит от .
.
Доказательство.
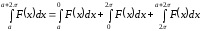 .
.
В последнем интеграле сделаем замену переменной
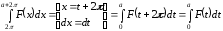 ,
,
что следует из периодичности подынтегральной функции. Тогда
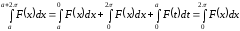 .
.
Теорема доказана,
поскольку
 .
.
Пусть
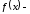
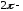 периодическая,
кусочно-дифференцируемая функция,
следовательно, она разложима в ряд Фурье
периодическая,
кусочно-дифференцируемая функция,
следовательно, она разложима в ряд Фурье
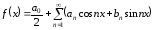 .
.
Определим
коэффициенты этого разложения, для чего
умножим обе части равенства на
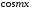 и проинтегрируем в пределах от
и проинтегрируем в пределах от до
до .
Тогда
.
Тогда
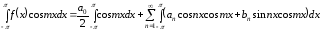 .
.
Из ортогональности
системы тригонометрических функций,
это было доказано выше, следует, что
интеграл
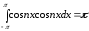 ,
а все остальные интегралы в правой
части равенства равны нулю. В этом случае
,
а все остальные интегралы в правой
части равенства равны нулю. В этом случае
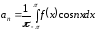 .
.
Нетрудно заметить,
что полученная формула справедлива для
 .
.
Умножим обе части
исходной формулы на
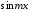 и проинтегрируем в тех же пределах
и проинтегрируем в тех же пределах
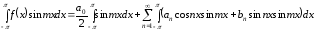 .
.
Также из
ортогональности рассматриваемых функций
следует
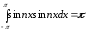 ,
все остальные интегралы в правой части
равенства равны нулю, отсюда имеем
,
все остальные интегралы в правой части
равенства равны нулю, отсюда имеем
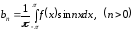 .
.
Здесь при интегрировании использовалась только что доказанная теорема.
Таким образом,
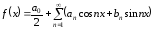 ,
,
причем
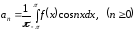 ,
,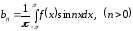 .
.
Разложение в ряд
Фурье
 периодической
функции
периодической
функции
Обобщим полученный
результат на функции с периодом
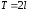 .
Очевидно, такая возможность несколько
расширяет область применимости рядов
Фурье.
.
Очевидно, такая возможность несколько
расширяет область применимости рядов
Фурье.
Пусть дана
кусочно-дифференцируемая, периодическая
с периодом
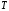 функция, то есть удовлетворяющая условию
функция, то есть удовлетворяющая условию .
Перейдем от переменной
.
Перейдем от переменной к переменной
к переменной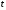 ,
считая при этом
,
считая при этом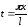 .
Тогда функция
.
Тогда функция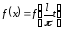 ,
причем
,
причем осталась периодической, но ее период
стал
осталась периодической, но ее период
стал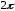 .
Проверим это:
.
Проверим это:
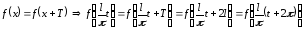 .
.
Отсюда имеем
 ,
что требовалось доказать.
,
что требовалось доказать.
Теперь воспользуемся
разложением в ряд Фурье
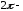 периодической
функции
периодической
функции
 ,
,
причем
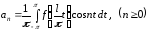 ,
,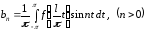 .
.
Сделаем обратную
замену
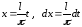 ,
тогда
,
тогда
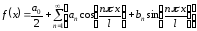 ,
,
при этом
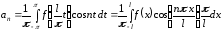 ,
,
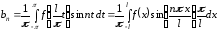 .
.
Таким образом,
 периодическая,
кусочно-дифференцируемая функция может
быть представлена в виде ряда Фурье
периодическая,
кусочно-дифференцируемая функция может
быть представлена в виде ряда Фурье
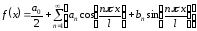 ,
,
Где
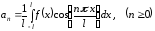 ,
,  .
.
Разложение в ряд Фурье четной, или нечетной
периодической функции
Лемма 1.
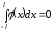 ,
если подынтегральная функция нечетна.
,
если подынтегральная функция нечетна.
Доказательство.
Очевидно,
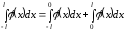 ,
сделаем в первом интеграле правой части
замену переменной с учетом того, что
,
сделаем в первом интеграле правой части
замену переменной с учетом того, что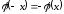 ,
,
 .
.
Тогда
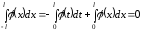 .
Доказано.
.
Доказано.
Лемма 2.
 ,
если подынтегральная функция четна.
,
если подынтегральная функция четна.
Доказательство.
В первом интеграле правой части равенства
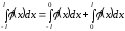 сделаем ту же замену переменной с учетом
четности подынтегральной функции
сделаем ту же замену переменной с учетом
четности подынтегральной функции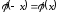 ,
тогда
,
тогда
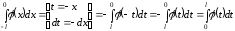 .
.
В результате
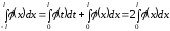 .
.
Разложение четной функции
1а). Имеем четную,
периодическую с периодом
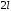 функцию
функцию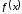 .
Воспользуемся ее представлением рядом
Фурье
.
Воспользуемся ее представлением рядом
Фурье
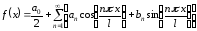 ,
,
где
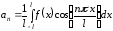 ,
, 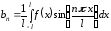 .
.
Поскольку
 - четная функция,
- четная функция,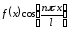 также четная функция как произведение
четных функций, а
также четная функция как произведение
четных функций, а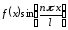 - нечетная как произведение четной и
нечетной функций. В соответствии с
леммами 1 и 2, имеем
- нечетная как произведение четной и
нечетной функций. В соответствии с
леммами 1 и 2, имеем ,
тогда
,
тогда
 ,
,
где
 .
.
1в). Если
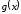 - четная,
- четная,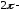 периодическая,
кусочно-дифференцируемая функция, как
частный случай получаем
периодическая,
кусочно-дифференцируемая функция, как
частный случай получаем
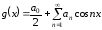 ,
,
причем 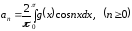 .
.
Разложение нечетной функции
2а). Пусть
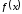 - нечетная, периодическая с периодом
- нечетная, периодическая с периодом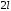 функция. Воспользуемся формулами
функция. Воспользуемся формулами
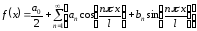 ,
,
где
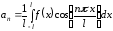 ,
,  .
.
Поскольку в первом
интеграле подынтегральная функция
нечетна, а во втором четна, то
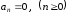 ,
и
,
и
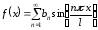 ,
,
где
 .
.
2в). Для нечетной,
периодической с периодом
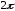 функции имеем
функции имеем
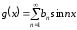 ,
,
где
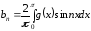 .
.
Разложение в ряд Фурье непериодической функции,
заданной в некотором промежутке
I.
Пусть кусочно-дифференцируемая функция
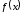 интересует нас только в промежутке
интересует нас только в промежутке .
Как представить ее в виде ряда Фурье?
Поскольку разложение непериодической
функции в ряд Фурье невозможно, поступают
следующим образом. Вместо заданной на
интервале
.
Как представить ее в виде ряда Фурье?
Поскольку разложение непериодической
функции в ряд Фурье невозможно, поступают
следующим образом. Вместо заданной на
интервале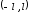 функции рассматривается периодическая
с периодом
функции рассматривается периодическая
с периодом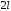 функция
функция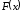 ,
которая периодически продолжает функцию
,
которая периодически продолжает функцию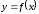 на всю числовую ось, то есть на каждом
интервале длиной
на всю числовую ось, то есть на каждом
интервале длиной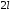 всей числовой оси она принимает значение
всей числовой оси она принимает значение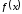 .
.
Теперь функция
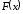 ,
как периодическая, может быть представлена
в виде ряда Фурье
,
как периодическая, может быть представлена
в виде ряда Фурье
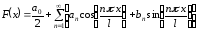 ,
,
где
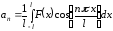 ,
, 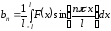 .
.
Но при определении
коэффициентов разложения интегрирование
происходит на интервале
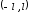 ,
где функции
,
где функции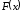 и
и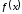 совпадают, следовательно, в этом
промежутке одну из этих функций можно
заменять другой. Совершив замену
функций, получаем, что в промежутке
совпадают, следовательно, в этом
промежутке одну из этих функций можно
заменять другой. Совершив замену
функций, получаем, что в промежутке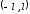 можно использовать разложение
можно использовать разложение
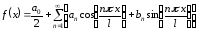 ,
,
где
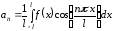 ,
, 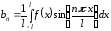 .
.
При этом возникают
некоторые проблемы. Вне промежутка
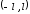 и на его границах значения функций
и на его границах значения функций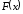 и
и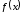 различаются. Известно, что
различаются. Известно, что
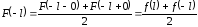 ,
,
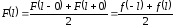 .
.
Таким образом, на
границах интервала
 значения функций
значения функций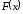 и
и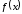 совпадают только в случае
совпадают только в случае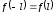 .
.
Вне интервала
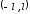 функции
функции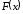 и
и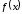 ,
как правило, вообще не имеют ничего
общего.
,
как правило, вообще не имеют ничего
общего.
В итоге, если
исследователя интересуют только
внутренние точки интервала
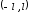 и не важно различие значений функций
и не важно различие значений функций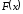 и
и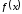 на границах этой области, для непериодической
функции можно использовать разложение
на границах этой области, для непериодической
функции можно использовать разложение
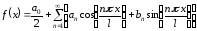 ,
,
где
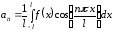 ,
, 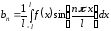 ,
,
причем в определении
коэффициентов ряда функция
 фактически не участвует.
фактически не участвует.
Пример замены
заданной в промежутке
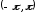 функции
функции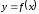 периодической функцией
периодической функцией приведен на рисунках 50 и 51.
приведен на рисунках 50 и 51.

Рисунок 50. Рисунок 51.
Пример. Разложить
в ряд Фурье функцию
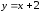 на интервале
на интервале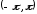 .
.
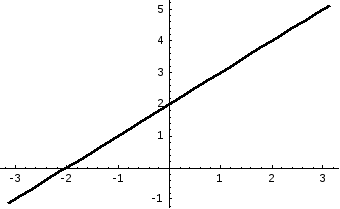
Рисунок 52.
Очевидно,
 ,
,
причем
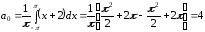 ,
,
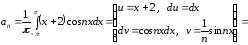
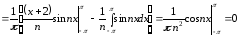 ,
,
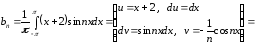
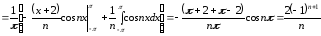 .
.
Тогда
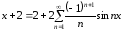 .
.
Нетрудно заметить,
что функция
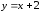 на границах интервала принимает значения
на границах интервала принимает значения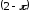 и
и ,
тогда как ряд Фурье на обеих границах
дает значение 2.
,
тогда как ряд Фурье на обеих границах
дает значение 2.
II.
Пусть кусочно-дифференцируемая
непериодическая функция
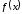 рассматривается в промежутке
рассматривается в промежутке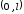 .
В этом случае необходимо продолжить
заданную функцию на интервал
.
В этом случае необходимо продолжить
заданную функцию на интервал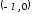 ,
затем применить процедуру, описанную
в пунктеI.
Поскольку на область
,
затем применить процедуру, описанную
в пунктеI.
Поскольку на область
 функция может быть продолжена произвольным
образом, появляется несколько вариантов
продолжения, и при решении конкретной
задачи можно использовать наиболее
удобный из них. Рассмотрим несколько
вариантов продолжения. Один из них –
продолжить функцию так, чтобы она стала
четной, тогда разложение в ряд будет
содержать только косинусы. Второй
вариант – продолжить функцию так, чтобы
она стала нечетной, ряд Фурье будет
содержать только синусы. Третий вариант
– считать в области
функция может быть продолжена произвольным
образом, появляется несколько вариантов
продолжения, и при решении конкретной
задачи можно использовать наиболее
удобный из них. Рассмотрим несколько
вариантов продолжения. Один из них –
продолжить функцию так, чтобы она стала
четной, тогда разложение в ряд будет
содержать только косинусы. Второй
вариант – продолжить функцию так, чтобы
она стала нечетной, ряд Фурье будет
содержать только синусы. Третий вариант
– считать в области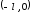 функцию равной нулю, тогда в ряде Фурье
будут присутствовать и синусы, и косинусы,
а при определении коэффициентов
разложения интегрирование будет
проводиться от 0 до
функцию равной нулю, тогда в ряде Фурье
будут присутствовать и синусы, и косинусы,
а при определении коэффициентов
разложения интегрирование будет
проводиться от 0 до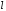 .
Возможны и другие варианты продолжения
функции.
.
Возможны и другие варианты продолжения
функции.
В разложении в ряд Фурье с помощью МАКСИМЫ используются следующие команды
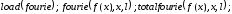
Первая команда показывает, что имеет место разложение в ряд Фурье, вторая команда задает разлагаемую функцию, переменную разложения и полупериод разложения. На выходе выдаются коэффициенты ряда Фурье. Третья команда выдает, и коэффициенты, и весь ряд Фурье.
Пример. Разложить
в ряд Фурье функцию
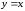 ,
заданную на интервале
,
заданную на интервале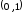 .
Рассмотрим два варианта решения.
.
Рассмотрим два варианта решения.
А) Продолжим функцию
на область
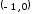 естественным образом, то есть рассмотрим
ее на интервале
естественным образом, то есть рассмотрим
ее на интервале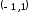 .
Поскольку
.
Поскольку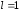 ,
а функция нечетна, ее разложение имеет
вид
,
а функция нечетна, ее разложение имеет
вид
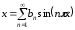 ,
,
где
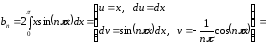
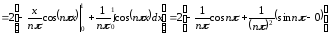
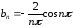
Тогда
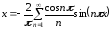 .
.
Заметим, что в
граничных точках интервала
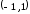 сама функция
сама функция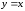 принимает значения
принимает значения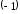 и 1 а ряд Фурье в этих точках дает
значение, равное 0.
и 1 а ряд Фурье в этих точках дает
значение, равное 0.
Разложение с помощью МАКСИМЫ функции, заданной на интервале,

Отметим, что в
последней команде приводится общий вид
коэффициента
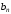 и упрощенный вариант, учитывающий, чтоn
– целое.
и упрощенный вариант, учитывающий, чтоn
– целое.
В) Продолжим на
интервал
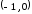 функцию как четную, тогда ее график
будет совпадать с графиком функции
функцию как четную, тогда ее график
будет совпадать с графиком функции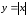 :
:
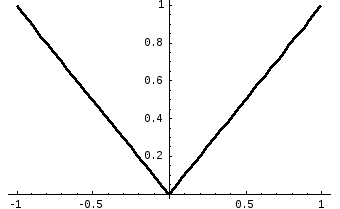
Рисунок 53.
В этом случае
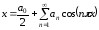 ,
,
причем
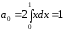 ,
,
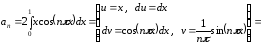
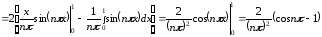 .
.
Очевидно,
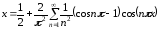 .
.
При помощи МАКСИМЫ
разложим функцию
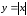 ,
или функцию
,
или функцию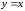 ,
заданную на интервале
,
заданную на интервале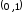 ,
продолженную на область
,
продолженную на область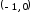 как четную
как четную

Примеры для самостоятельного решения
Разложить в ряды Фурье на указанных интервалах следующие функции
16.9.
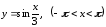 ,
16.10.
,
16.10. ,
,
16.11.
 ,
продолжив ее как четную,
,
продолжив ее как четную,
16.12.
 ,
продолжив ее как нечетную.
,
продолжив ее как нечетную.
Интеграл Фурье
Еще один вариант
представления непериодической функции
в виде ряда Фурье заключается в том, что
период функции принимается
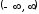 .
Тогда ряд Фурье переходит в интеграл
Фурье. Покажем, как это делается.
.
Тогда ряд Фурье переходит в интеграл
Фурье. Покажем, как это делается.
Запишем вначале
ряд Фурье для промежутка

 ,
,
где
 ,
, 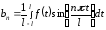 .
.
При определении
коэффициентов интегрирование по
переменной
 заменено интегрированием по
заменено интегрированием по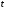 ,
что не меняет сути дела, но необходимо
для дальнейшего вывода формул. Подставляем
значения коэффициентов в ряд
,
что не меняет сути дела, но необходимо
для дальнейшего вывода формул. Подставляем
значения коэффициентов в ряд
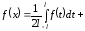
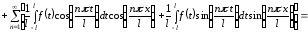
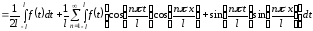 ,
,
откуда следует
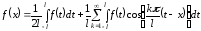 .
(*)
.
(*)
Пусть функция
 определена на промежутке
определена на промежутке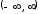 и разложима на интервале
и разложима на интервале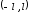 при любом, сколь угодно большом, значении
при любом, сколь угодно большом, значении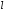 .
Осуществим переход к пределу в формуле
(*) при
.
Осуществим переход к пределу в формуле
(*) при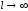 .
Интеграл
.
Интеграл должен принимать конечное значение, в
противном случае разложение в ряд Фурье
невозможно, тогда первое слагаемое в
формуле (*) при
должен принимать конечное значение, в
противном случае разложение в ряд Фурье
невозможно, тогда первое слагаемое в
формуле (*) при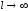 стремится к нулю. Преобразуем оставшийся
член, обозначив,
стремится к нулю. Преобразуем оставшийся
член, обозначив,
 ,
,
что равносильно
разбиению интервала
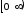 на равные отрезки длиной
на равные отрезки длиной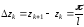 .
Тогда второе слагаемое суммы (*) принимает
вид
.
Тогда второе слагаемое суммы (*) принимает
вид
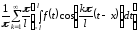
или
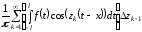 .
.
Полученное выражение
очень напоминает интегральную сумму
Римана для функции
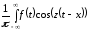 на интервале
на интервале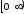 .
Переходя к пределу при
.
Переходя к пределу при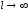 ,
получаем
,
получаем
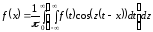 .
.
С помощью формулы для косинуса разности полученное соотношение можно представить следующим образом
 ,
,
где
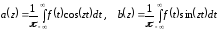 .
.
Таким образом,
получено представление функции
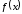 через интеграл Фурье. Имеет место
теорема, которая утверждает, что если
эта функция кусочно-дифференцируема в
каждом конечном промежутке и абсолютно
интегрируема в промежутке
через интеграл Фурье. Имеет место
теорема, которая утверждает, что если
эта функция кусочно-дифференцируема в
каждом конечном промежутке и абсолютно
интегрируема в промежутке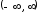 ,
то в любой точке промежутка
,
то в любой точке промежутка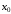 ее интеграл Фурье сходится и имеет
значение
ее интеграл Фурье сходится и имеет
значение
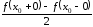 .
.
Для непрерывной
в области
 функции интеграл Фурье сходится и
принимает значение
функции интеграл Фурье сходится и
принимает значение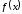 .
.
