Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Казанский федеральный университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

ruffus.doc

Скачиваний:

Добавлен:

24.08.2019

Размер:

185.34 Кб

Скачать

☆

1 / 21 2 > Следующая >>>

Казанский государственный университет

КУРСОВАЯ РАБОТА

по дисциплине:

Численные методы

Работу выполнил:

студент группы 938

Трагер Д. Н.

Работу проверила:

Гнеденкова В.Л.

Казань - 2006

ЧИСЛЕННЫЕ МЕТОДЫ.

Семестровое задание.

Вариант №5.

I. Постановка задачи

Имеется функция – интегральный косинус: . Необходимо изучить и сравнить различные способы её приближённого вычисления. Для этого надо выполнить следующие задания:

протабулировать на отрезке с шагом и точностью , основываясь на ряде Тейлора, предварительно вычислив его по формуле: , где ;
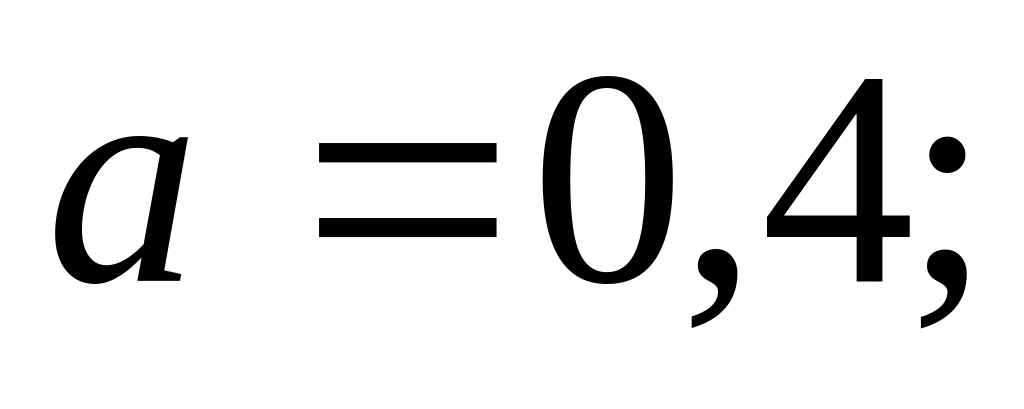
по полученной таблице значений построить интерполяционный полином Лагранжа, приближающий : и вычислить погрешность интерполирования ;
на той же сетке узлов построить таблицу приближённых значений , используя составную квадратурную формулу центральных прямоугольников: , где , а - точки разбиения отрезка интерполирования на N частей, . Интеграл вычислить с точностью , которая считается достигнутой, если ;
построить таблицу обратной к функции следующим итерационным методом (метод секущих): решение уравнения находится по формуле . В качестве начального приближения к точке взять .

II. Решение и анализ

Для начала изучим сходимость ряда. Так как ряд является степенным, то мы можем вычислить радиус его сходимости следующим способом:

, где - это коэффициент степенного ряда с номером n. Имеем , поэтому ряд сходится на всей числовой оси. Следовательно, мы можем табулировать его на любом отрезке.

1) Значения, полученные вычислением суммы ряда в узлах табуляции, являются опорными и служат в дальнейшем сравнений и вычислений погрешностей.

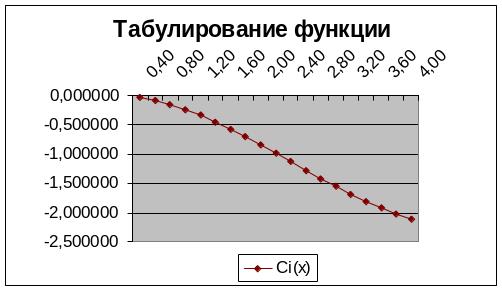
Табулирование исходной функции:

X: Ci(x):

0.40 -0.039733

0.60 -0.088661

0.80 -0.155794

1.00 -0.239812

1.20 -0.339078

1.40 -0.451681

1.60 -0.575487

1.80 -0.708191

2.00 -0.847383

2.20 -0.990598

2.40 -1.135393

2.60 -1.279390

2.80 -1.420347

3.00 -1.556198

3.20 -1.685109

3.40 -1.805510

3.60 -1.916124

3.80 -2.015995

4.00 -2.104491

2) Первый полином Лагранжа строится на начальных узлах табуляции. Второй раз он строится по специально выбранным узлам, являющимися корнями полиномов Чебышёва и вычисляемых по формуле: . Оба раза сравнение полинома с функцией проводится в точках, лежащих между узлами табуляции. Нижеприведённые графики наглядно показывают, что полином Чебышева даёт минимальную погрешность вычисления.

Погрешность интерполяционного полинома Лагранжа, построенного по начальным узлам табуляции (погрешность считается по точкам, находящимся между узлами начальной табуляции):

X: Ошибка:

0.50 0.00038080

0.70 0.00003859

0.90 0.00000684

1.10 0.00000205

1.30 0.00000101

1.50 0.00000005

1.70 0.00000015

1.90 0.00000024

2.10 0.00000038

2.30 0.00000010

2.50 0.00000001

2.70 0.00000041

2.90 0.00000038

3.10 0.00000064

3.30 0.00000163

3.50 0.00000487

3.70 0.00003130

3.90 0.00032595

Наибольшая погрешность: 0.00038080.

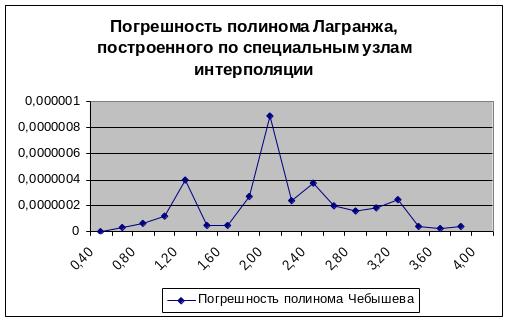
Погрешность интерполяционного полинома Лагранжа по спец. узлам интерполяции (считается по точкам, находящимся между узлами начальной табуляции):

X: Ошибка:

0.50 0.00000000

0.70 0.00000003

0.90 0.00000006

1.10 0.00000012

1.30 0.00000040

1.50 0.00000005

1.70 0.00000005

1.90 0.00000027

2.10 0.00000089

2.30 0.00000024

2.50 0.00000037

2.70 0.00000020

2.90 0.00000016

3.10 0.00000018

3.30 0.00000025

3.50 0.00000004

3.70 0.00000002

3.90 0.00000004

Наибольшая погрешность: 0.00000089.

3) Приближённые вычисления интеграла в узлах табуляции проводятся 4 раза с вычислениями по формулам центральных прямоугольников, трапеций, Симпсона и Гаусса соответственно. При вычислении интеграла по формуле трапеций возникает необходимость в использовании значения , где - это подынтегральная функция, но . Имеем 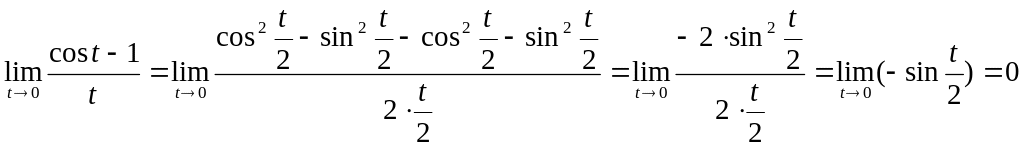. Графики показывают погрешность вычисления интегралов по каждому из методов. Видно, что наилучшей по погрешности является формула Гаусса, а наихудшей – формула трапеций.

X: Ф-ла ЦП: N: Ошибка: Ф-ла трапеций: N: Ошибка:

0.40 -0.039736 8 0.000003 -0.039730 8 0.000003

0.60 -0.088671 8 0.000010 -0.088640 8 0.000021

0.80 -0.155826 8 0.000032 -0.155777 16 0.000017

1.00 -0.239831 16 0.000019 -0.239802 32 0.000010

1.20 -0.339088 32 0.000010 -0.339059 32 0.000019

1.40 -0.451699 32 0.000018 -0.451673 64 0.000008

1.60 -0.575516 32 0.000029 -0.575472 64 0.000014

1.80 -0.708202 64 0.000011 -0.708169 64 0.000022

2.00 -0.847398 64 0.000016 -0.847350 64 0.000033

2.20 -0.990621 64 0.000023 -0.990587 128 0.000011

2.40 -1.135423 64 0.000031 -1.135378 128 0.000015

2.60 -1.279400 128 0.000010 -1.279371 128 0.000019

2.80 -1.420359 128 0.000012 -1.420322 128 0.000025

3.00 -1.556214 128 0.000015 -1.556167 128 0.000031

3.20 -1.685128 128 0.000018 -1.685100 256 0.000010

3.40 -1.805531 128 0.000021 -1.805498 256 0.000012

3.60 -1.916149 128 0.000025 -1.916111 256 0.000013

3.80 -2.016024 128 0.000029 -2.015980 256 0.000014

4.00 -2.104524 128 0.000033 -2.104476 256 0.000016

X: Ф-ла Симпсона: N: Ошибка: Ф-ла Гаусса: N: Ошибка:

0.40 -0.039734 8 0.000001 -0.039734 8 0.000001

0.60 -0.088661 8 0.000000 -0.088661 8 0.000000

0.80 -0.155793 8 0.000001 -0.155793 8 0.000001

1.00 -0.239812 8 0.000000 -0.239812 8 0.000000

1.20 -0.339078 8 0.000000 -0.339078 8 0.000000

1.40 -0.451681 8 0.000001 -0.451681 8 0.000001

1.60 -0.575487 8 0.000000 -0.575487 8 0.000000

1.80 -0.708191 8 0.000000 -0.708191 8 0.000000

2.00 -0.847382 8 0.000000 -0.847382 8 0.000001

2.20 -0.990599 8 0.000001 -0.990598 8 0.000000

2.40 -1.135394 8 0.000001 -1.135392 8 0.000000

2.60 -1.279392 8 0.000002 -1.279390 8 0.000000

2.80 -1.420349 8 0.000002 -1.420345 8 0.000001

3.00 -1.556201 8 0.000003 -1.556196 8 0.000002

3.20 -1.685113 8 0.000004 -1.685106 8 0.000003

3.40 -1.805514 8 0.000004 -1.805506 8 0.000004

3.60 -1.916130 8 0.000007 -1.916120 8 0.000004

3.80 -2.015995 16 0.000001 -2.015989 8 0.000005

4.00 -2.104492 16 0.000001 -2.104485 16 0.000000

4) Отыскание обратных функции ведётся методом секущих с погрешностью . По методу секущих в качестве начального приближения к точке берётся , что обеспечивает эффективный поиск корней уравнения . Для вычисления производной функции в точке, используется встроенная процедура, которая производит вычисления с помощью дифференцирования ряда Тейлора исходной функции по формуле: .