
Определения
Ряды в настоящее время представляют собой особо широко используемый математический аппарат для точного и приближенного решения различных уравнений.
Определение 1. Рядом называется сумма некоторой последовательности, другими словами ряд – есть сумма бесконечного числа членов, каждый из которых является элементом заданной последовательности.
Ряды бывают двух видов:
1) числовые ряды, если каждый член ряда – число, в этом случае
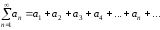 ,
,
причем в правой
части записан числовой ряд, в левой
части – его сокращенное обозначение,
здесь
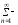 означает
суммирование членов ряда от первого до
сколь угодно большого,
означает
суммирование членов ряда от первого до
сколь угодно большого, общий
(
общий
(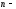 й)
член ряда.
й)
член ряда.
2) функциональные ряды, когда каждый член ряда есть функция:

Определение 2. Ряд называется сходящимся, если его сумма имеет конечное значение, если сумма ряда не существует, или равна бесконечности, ряд – расходящийся.
Определение
3. Сумму
 первых членов ряда называют
первых членов ряда называют частичной суммой ряда
частичной суммой ряда .
.
Очевидно, сумма
ряда
 определяется формулой
определяется формулой .
Однако применение этой формулы сопряжено
с большими, порой непреодолимыми,
трудностями. Далеко не всегда удается
в компактной форме записать
.
Однако применение этой формулы сопряжено
с большими, порой непреодолимыми,
трудностями. Далеко не всегда удается
в компактной форме записать ю
частичную сумму ряда, а, следовательно,
вычислить ее предел. Почленное суммирование
ряда - еще менее перспективная процедура,
бесконечное число членов не просуммируешь.
ю
частичную сумму ряда, а, следовательно,
вычислить ее предел. Почленное суммирование
ряда - еще менее перспективная процедура,
бесконечное число членов не просуммируешь.
Вследствие этого точное значение суммы ряда можно установить в очень небольшом числе случаев.
Приведем пример геометрической прогрессии
 ,
,
знаменатель которой
 .
.
Известна сумма
первых
 членов этого ряда
членов этого ряда .
Вычислим ее предел
.
Вычислим ее предел .
Если
.
Если ,
то
,
то ,
следовательно,
,
следовательно, .
При
.
При
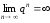 ,
и
,
и .
Ряд расходится. При
.
Ряд расходится. При ряд также расходится. Итак, подтверждается
утверждение, что геометрическая
прогрессия сходится при
ряд также расходится. Итак, подтверждается
утверждение, что геометрическая
прогрессия сходится при и расходится при
и расходится при .
.
В большинстве случаев приходится вычислять суммы рядов приближенно, но для этого необходимо знать, существует ли конечное значение этой суммы, то есть сходящийся ли ряд.
Теория рядов, следовательно, создана для установления сходимости или расходимости рядов. При необходимости сумму сходящегося ряда вычисляют приближенно, расходящиеся ряды практической ценности не представляют.
Числовые ряды Необходимое условие сходимости ряда
Если ряд сходится,
то
 .
.
Доказательство.
Если ряд сходящийся, существует его
конечная сумма
 ,
причем
,
причем .
Вычислим
.
Вычислим
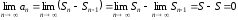 .
.
Основное свойство рядов
Если ряд сходящийся,
то его остаток
 ,
образованный отбрасыванием первых
,
образованный отбрасыванием первых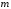 членов ряда, тоже сходится. Если ряд
расходящийся, то его остаток также
является расходящимся рядом.
членов ряда, тоже сходится. Если ряд
расходящийся, то его остаток также
является расходящимся рядом.
В самом деле,
 .
.
Если ряд сходится,
то существует его конечная сумма
 ,
а
,
а -
всегда конечна как сумма конечного
числа членов. Тогда из
-
всегда конечна как сумма конечного
числа членов. Тогда из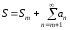 следует, что
следует, что конечное
число, и остаток ряда – сходится. Когда
ряд расходящийся,
конечное
число, и остаток ряда – сходится. Когда
ряд расходящийся, .
Поскольку сумма ряда в правой части
равенства не существует (ряд расходящийся),
а
.
Поскольку сумма ряда в правой части
равенства не существует (ряд расходящийся),
а имеет конечное значение, сумма ряда в
левой части также не существует.
имеет конечное значение, сумма ряда в
левой части также не существует.
Переходим к рассмотрению частных случаев рядов. Вначале исследуем сходимость числовых рядов.
Знакоположительные числовые ряды
Начнем с теорем сравнения знакоположительных рядов.
Первая теорема
сравнения.
Даны два знакоположительных числовых
ряда
 и
и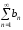 ,
причем
,
причем .
Из сходимости большего ряда следует
сходимость меньшего ряда. Из расходимости
меньшего ряда следует расходимость
большего ряда.
.
Из сходимости большего ряда следует
сходимость меньшего ряда. Из расходимости
меньшего ряда следует расходимость
большего ряда.
Доказательство.
1) Пусть ряд
 сходится, и его сумма
сходится, и его сумма конечна. Рассмотрим частичные суммы
обоих рядов
конечна. Рассмотрим частичные суммы
обоих рядов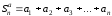 и
и .
Так как члены обоих рядов положительны,
при любом
.
Так как члены обоих рядов положительны,
при любом имеем
имеем ,
из условия
,
из условия имеем
имеем .
Рассмотрим последовательность частичных
сумм ряда
.
Рассмотрим последовательность частичных
сумм ряда .
Она монотонно возрастает с ростом
.
Она монотонно возрастает с ростом (суммируется все большее число
положительных членов). В то же время она
ограничена сверху числом
(суммируется все большее число
положительных членов). В то же время она
ограничена сверху числом .
Но имеется теорема, утверждающая, что
монотонно возрастающая и ограниченная
сверху последовательность имеет конечный
предел. Итак,
.
Но имеется теорема, утверждающая, что
монотонно возрастающая и ограниченная
сверху последовательность имеет конечный
предел. Итак, ,
следовательно,
,
следовательно, является суммой ряда
является суммой ряда .
.
2) Пусть ряд
 расходится. Поскольку все его члены
положительны, его сумма равна бесконечности.
По условию теоремы
расходится. Поскольку все его члены
положительны, его сумма равна бесконечности.
По условию теоремы ,
следовательно,
,
следовательно, ,
то есть при неограниченном возрастании
суммы
,
то есть при неограниченном возрастании
суммы неограниченно растет и сумма
неограниченно растет и сумма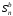 .
Больший ряд также расходится.
.
Больший ряд также расходится.
Вторая теорема
сравнения
(упрощенная постановка). Даны два
знакоположительных ряда
 и
и ,
причем
,
причем ,
в этом случае оба ряда ведут себя
одинаково: либо оба сходятся, либо оба
расходятся.
,
в этом случае оба ряда ведут себя
одинаково: либо оба сходятся, либо оба
расходятся.
Доказательство.
Из
 следует, что
следует, что
 .
.
Из записанной
формулы следует, что начиная с
 и для всех остальных выполняется
неравенство
и для всех остальных выполняется
неравенство ,
из которого имеем
,
из которого имеем ,
или
,
или .
.
1)Рассмотрим правую
часть неравенства. Пусть ряд
 сходится, тогда сходится и его остаток
сходится, тогда сходится и его остаток ,
следовательно, сходится и ряд
,
следовательно, сходится и ряд .
Поскольку
.
Поскольку ,
из первой части первой теоремы сравнения
следует сходимость ряда
,
из первой части первой теоремы сравнения
следует сходимость ряда ,
а, следовательно, и самого ряда
,
а, следовательно, и самого ряда .
.
2) Пусть ряд
 расходится, тогда расходится и его
остаток
расходится, тогда расходится и его
остаток .
Подберем
.
Подберем так, чтобы
так, чтобы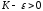 ,
тогда ряд
,
тогда ряд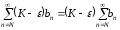 тоже расходится. Но из левой части
полученного выше неравенства следует,
что
тоже расходится. Но из левой части
полученного выше неравенства следует,
что ,
значит, члены ряда
,
значит, члены ряда больше членов расходящегося ряда, из
первой теоремы сравнения следует, что
ряд
больше членов расходящегося ряда, из
первой теоремы сравнения следует, что
ряд расходящийся, расходится и ряд
расходящийся, расходится и ряд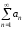 .
.
Доказано, что из
сходимости (расходимости) ряда
 следует сходимость (расходимость) ряда
следует сходимость (расходимость) ряда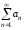 .
.
Рассмотрим теперь
 .
Очевидно,
.
Очевидно, ,
то есть условия только что доказанной
теоремы выполнены. Но в этом случае
можно утверждать, что из сходимости
(расходимости) ряда
,
то есть условия только что доказанной
теоремы выполнены. Но в этом случае
можно утверждать, что из сходимости
(расходимости) ряда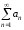 следует сходимость (расходимость) ряда
следует сходимость (расходимость) ряда .
Итак, ряды при выполнении условий теоремы
ведут себя одинаково.
.
Итак, ряды при выполнении условий теоремы
ведут себя одинаково.
Доказаны две важнейшие теоремы. Однако для сравнения рядов необходимо иметь информацию о сходимости или расходимости хотя бы нескольких рядов, с которыми можно было бы сравнивать другие ряды.
Для этой цели рассмотрим несколько достаточных условий, позволяющих исследовать сходимость конкретных рядов.
Признак Даламбера
сходимости знакоположетельных рядов
Теорема.
Ряд

 при условии
при условии сходится, когда
сходится, когда расходится, если
расходится, если признак Даламбера неприменим.
признак Даламбера неприменим.
Доказательство.
Если
 ,
то
,
то
 ,
,
откуда следует

1) Для доказательства
первой части теоремы воспользуемся
правой частью неравенства, записав его
в виде
 ,
где
,
где ,
, .
По условию теоремы
.
По условию теоремы .
Зададим
.
Зададим настолько малым, чтобы
настолько малым, чтобы .
Тогда
.
Тогда
 ,
,
 ,
,
 ,
,
……………………
Рассмотрим теперь два ряда

и
 .
.
Нижний ряд
представляет собой сходящуюся
геометрическую прогрессию, так как
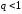 .
Члены верхнего ряда меньше соответствующих
членов нижнего ряда, на основании первой
теоремы сравнения ряд
.
Члены верхнего ряда меньше соответствующих
членов нижнего ряда, на основании первой
теоремы сравнения ряд сходится. Но этот ряд является остатком
рассматриваемого ряда
сходится. Но этот ряд является остатком
рассматриваемого ряда ,
следовательно, он тоже сходится.
,
следовательно, он тоже сходится.
2) Для доказательства
второй части теоремы при
 воспользуемся полученным ранее
неравенством, подобрав
воспользуемся полученным ранее
неравенством, подобрав так, чтобы
так, чтобы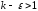 .
Тогда
.
Тогда ,
то есть положительные члены ряда растут
с ростом
,
то есть положительные члены ряда растут
с ростом .
Очевидно,
.
Очевидно, ,
но ряд может сходиться только в случае
,
но ряд может сходиться только в случае .
Ряд расходится.
.
Ряд расходится.
3) При условии невозможно доказать сходимость, или
расходимость ряда. Следовательно, в
этом случае признак Даламбера неприменим.
невозможно доказать сходимость, или
расходимость ряда. Следовательно, в
этом случае признак Даламбера неприменим.
Рекомендация. Признак Даламбера дает положительный ответ практически всегда, если общий член ряда содержит показательную функцию или факториалы.
Пример 1.
 .
Очевидно,
.
Очевидно, .
Тогда
.
Тогда
 .
Ряд сходится.
.
Ряд сходится.
Пример 2.
 .
.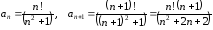 .
.
Чтобы
решить этот пример, вспомним некоторые
формулы для "факториала"
 ,
,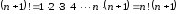 .
.
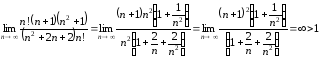 .
.
Ряд расходится.
Радикальный признак Коши
сходимости знакоположительных рядов
Теорема.
Дан ряд

 .
Если
.
Если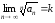 , а
, а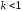 ,
то ряд сходится, при
,
то ряд сходится, при ряд расходится, при
ряд расходится, при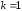 признак
не работает.
признак
не работает.
Доказательство.
Из
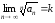 следует, что
следует, что
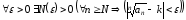 ,
,
другими словами,
начиная с некоторого
 и для всех последующих
и для всех последующих ,
оттуда следует
,
оттуда следует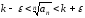 ,
или
,
или ,
где
,
где ,
,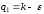 .
.
1. Докажем
справедливость первого утверждения
теоремы. В этом случае
 ,
зададим
,
зададим так, чтобы выполнялось
так, чтобы выполнялось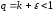 .
Из правой части полученного двойного
неравенства следует, что
.
Из правой части полученного двойного
неравенства следует, что .
Если сравнить ряды
.
Если сравнить ряды и
и ,
то члены первого ряда меньше соответствующих
членов второго ряда, являющегося
сходящимся как геометрическая прогрессия
со знаменателем меньшим единицы. Из
первой теоремы сравнения рядов следует,
что ряд
,
то члены первого ряда меньше соответствующих
членов второго ряда, являющегося
сходящимся как геометрическая прогрессия
со знаменателем меньшим единицы. Из
первой теоремы сравнения рядов следует,
что ряд ,
то есть остаток ряда
,
то есть остаток ряда сходится, следовательно, сходится и сам
ряд.
сходится, следовательно, сходится и сам
ряд.
2. При доказательстве
второго утверждения теоремы учтем, что
 и зададим
и зададим так, чтобы
так, чтобы .
Воспользуемся левой частью двойного
неравенства
.
Воспользуемся левой частью двойного
неравенства .
Сравним ряд
.
Сравним ряд с расходящейся геометрической прогрессией
с расходящейся геометрической прогрессией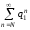 .
И поскольку члены ряда
.
И поскольку члены ряда больше соответствующих членов расходящейся
геометрической прогрессии, он расходится.
Так как этот ряд является остатком ряда
больше соответствующих членов расходящейся
геометрической прогрессии, он расходится.
Так как этот ряд является остатком ряда ,
то и сам ряд расходится.
,
то и сам ряд расходится.
3. При
 ряд может как сходиться, так и расходиться,
следовательно, признак неприменим.
ряд может как сходиться, так и расходиться,
следовательно, признак неприменим.
Замечание.
Радикальный признак удобно применять,
когда хорошо извлекается корень
 й
степени из общего члена ряда.
й
степени из общего члена ряда.
Пример 1.
 .
. ,
ряд сходится.
,
ряд сходится.
Пример 2.
 .
.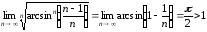 ,
,
ряд расходится.
Интегральный признак Маклорена – Коши
сходимости знакоположительных рядов
Теорема.
Знакоположительный ряд
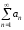 сходится
(расходится), если сходится (расходится)
интеграл
сходится
(расходится), если сходится (расходится)
интеграл ,
причем подынтегральная функция
,
причем подынтегральная функция получается из общего члена ряда заменой
дискретно меняющейся переменной
получается из общего члена ряда заменой
дискретно меняющейся переменной на действительную переменную
на действительную переменную .
.
Доказательство.
1) Пусть интеграл
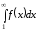 - сходится, то есть принимает конечное
значение. Рассмотрим интеграл
- сходится, то есть принимает конечное
значение. Рассмотрим интеграл ,
его значение дает площадь криволинейной
трапеции, ограниченной прямыми
,
его значение дает площадь криволинейной
трапеции, ограниченной прямыми ,
, ,
, и кривой
и кривой .
Разобьем отрезок
.
Разобьем отрезок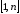 на
на равных частей, длина каждого элементарного
отрезка равна 1. Из точек разбиения
восстановим перпендикуляры до пересечения
с кривой, длины этих перпендикуляров
равных частей, длина каждого элементарного
отрезка равна 1. Из точек разбиения
восстановим перпендикуляры до пересечения
с кривой, длины этих перпендикуляров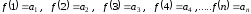 ,
где
,
где -
члены исследуемого ряда, что следует
из условия теоремы. Построим вписанные
в криволинейную трапецию прямоугольники,
одна из сторон каждого из них равна 1,
другие имеют длины
-
члены исследуемого ряда, что следует
из условия теоремы. Построим вписанные
в криволинейную трапецию прямоугольники,
одна из сторон каждого из них равна 1,
другие имеют длины соответственно. Подсчитаем сумму
площадей вписанных прямоугольников
соответственно. Подсчитаем сумму
площадей вписанных прямоугольников
 ,
,
сумма площадей
численно равна
 й
частичной сумме ряда без первого члена.
Рассмотрим последовательность частичных
сумм ряда. Она растет с ростом величины
верхнего предела интеграла, так как
растет количество вписанных прямоугольников.
В то же время любая частичная сумма
ряда, как уже говорилось выше, совпадающая
численно с площадью вписанных
прямоугольников, не может превышать
площади криволинейной трапеции, которая
сама меньше значения интеграла
й
частичной сумме ряда без первого члена.
Рассмотрим последовательность частичных
сумм ряда. Она растет с ростом величины
верхнего предела интеграла, так как
растет количество вписанных прямоугольников.
В то же время любая частичная сумма
ряда, как уже говорилось выше, совпадающая
численно с площадью вписанных
прямоугольников, не может превышать
площади криволинейной трапеции, которая
сама меньше значения интеграла .
Итак, последовательность частичных
сумм ряда монотонно возрастает и
ограничена сверху, следовательно, она
имеет конечный предел
.
Итак, последовательность частичных
сумм ряда монотонно возрастает и
ограничена сверху, следовательно, она
имеет конечный предел ,
но это сумма ряда
,
но это сумма ряда по определению. Значит, ряд сходится.
по определению. Значит, ряд сходится.
2) Пусть интеграл
 расходящийся. Так как
расходящийся. Так как ,
то
,
то .
Построим описанные прямоугольники,
одна из сторон каждого из них равна 1,
другие соответственно
.
Построим описанные прямоугольники,
одна из сторон каждого из них равна 1,
другие соответственно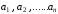 .
Сумма площадей этих прямоугольников
равна
.
Сумма площадей этих прямоугольников
равна и совпадает с
и совпадает с частичной
суммой ряда. Поскольку сумма площадей
описанных прямоугольников больше
площади криволинейной трапеции, которая
равна
частичной
суммой ряда. Поскольку сумма площадей
описанных прямоугольников больше
площади криволинейной трапеции, которая
равна ,
то и частичные суммы ряда неограниченно
возрастают. Очевидно,
,
то и частичные суммы ряда неограниченно
возрастают. Очевидно, .
Ряд расходится.
.
Ряд расходится.
Итак, получен универсальный признак сходимости, который, в отличие от предыдущих двух признаков, работает всегда. Но его применение приводит к необходимости исследования сходимости несобственного интеграла, что далеко не просто, да и не всегда возможно.
Исследуем ряд
 с помощью интегрального признака. Для
этого необходимо исследовать сходимость
интеграла
с помощью интегрального признака. Для
этого необходимо исследовать сходимость
интеграла ,
что было проделано ранее. Он сходится
при
,
что было проделано ранее. Он сходится
при и расходится при
и расходится при .
Тогда и ряд
.
Тогда и ряд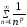 сходится при
сходится при и расходится при
и расходится при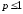 .
.
Пример 1.
 .
Вычислим интеграл
.
Вычислим интеграл
 ,
,
интеграл сходится и ряд тоже.
Пример 2.
 .
Вычислим интеграл
.
Вычислим интеграл

 ,
,
интеграл, а вместе с ним ряд сходятся.
Исследование сходимости знакоположительных рядов с помощью МАКСИМЫ
Рассмотрим ряд


Поскольку не выполняется необходимое условие сходимости ряда (предел n - го члена равен бесконечности), он расходящийся.
Рассмотрим ряд


Поскольку предел
n
- го члена
равен нулю, ряд может как сходиться, так
и расходиться. Применение признака
Даламбера дает
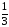 ,
что меньше 1, ряд сходится.
,
что меньше 1, ряд сходится.
Исследуем ряд


Проверка необходимого условия показывает, что ряд может и сходиться, и расходиться. Признак Даламбера дает 1, то есть не работает. Интегральный признак приводит к сходящемуся интегралу, следовательно, ряд сходится.
Примеры для самостоятельного решения
Исследовать сходимость рядов, используя теоремы сравнения и признаки сходимости
15.1.
 ,
15.2.
,
15.2. ,
15.3.
,
15.3. ,
15.4.
,
15.4. ,
,
15.5.
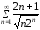 ,
15.6.
,
15.6. ,
15.7.
,
15.7. ,
15.8
,
15.8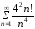 ,
,
15.9.
 ,
15.10.
,
15.10. ,
15.11.
,
15.11. ,
15.12.
,
15.12. .
.
Ответы. 15.1. Сходится. 15.2. Сходится. 15.3.Сходится. 15.4. Сходится.
15.5. Сходится. 15.6. Расходится. 15.7. Сходится. 15.8. Расходится.
15.9. Сходится. 15.10. Сходится. 15.11. Сходится. 15.12. Расходится.
