
4.9 А); б).
4.10
а)![]() ;
б)
;
б)![]() .
.
4.11
а)![]() ;б)
;б)
![]() .
.
4.12
а)![]() ;
б)
;
б)
![]() .
.
В задачах 4.13-4.21, выяснить какие из указанных функций четные, какие нечетные, а какие ни четные, ни нечетные.
4.13
![]() .
4.14
.
4.14
![]() .
4.15
.
4.15
![]()
4.16![]() .4.17
.4.17
![]() .
.
4.18![]() .4.19
.4.19
![]() .
.
4.20
![]() .4.21
.4.21
![]() .
.
В задачах 4.22-4.30 выяснить, какие из функций являются периодическими, и определить их наименьший период Т:
4.22
![]() 4.23
4.23![]() 4.24
4.24
![]()
4.25![]() 4.26
4.26![]()
4.27
![]() 4.28
4.28
![]()
4.29![]() 4.30
4.30
![]()
В задачах 4.31-4.34 доказать, что следующие функции являются монотонно возрастающими в указанных промежутках:
4.31
![]() 4.32
4.32![]() .
.
4.33![]() 4.34
4.34![]() .
.
В задачах 4.35-4.38 доказать, что следующие функции являются монотонно убывающими в указанных промежутках:
4.35
![]() 4.36
4.36
![]()
4.37
![]() .4.38
.4.38![]() .
.
В
задачах 4.39-4.46 найти
обратную функцию
![]() и её область определения:
и её область определения:
4.39![]() 4.40
4.40
![]() 4.41
4.41
![]() 4.42
4.42
![]()
4.43
![]() 4.44
4.44
![]() ,а)
,а)![]() ;б)
;б)![]()
4.45
![]() если:а)
если:а)
![]() б)
б)
![]() .
.
4.46
![]() если:а)
если:а)
![]() ;
б)
;
б)
![]() .
.
В
задачах 4.47-4.51 найти
композиции
![]() функций:
функций:
4.47
![]() 4.48
4.48
![]()
4.49
![]() 4.50
4.50
![]()
4.51
![]() ,
,
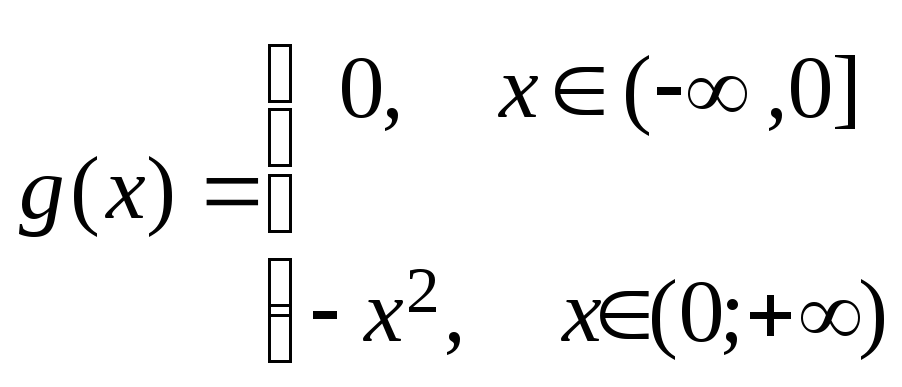 .
.
4.52
Найти
![]() .
.
4.53
Найти
![]() .
.
4.54
Функция
![]() определена при
определена при![]() Найти области определения функций:
Найти области определения функций:
а)
![]() ;
б)
;
б)![]() ;
в)
;
в)
![]() ;
г)
;
г)![]() .
.
§2. Графики элементарных функций.
Основными
элементарными функциями
считаются: степенная
функция
![]() ,показательная
функция
,показательная
функция
![]() (
(![]() ,
,![]() ),логарифмическая
функция
),логарифмическая
функция
![]() (
(![]() ,
,![]() ),тригонометрические
функции
),тригонометрические
функции
![]() ,
,![]() ,
,![]() ,
,![]() ,обратные
тригонометрические
функции
,обратные
тригонометрические
функции
![]() ,
,![]() ,
,![]() ,
,![]() .
.
Элементарной
называется функция, полученная из
основных элементарных функций конечным
числом их арифметических операций и
композиций. Функции![]() ,
,![]() ,
,![]() ,
,![]() называются, соответственно,гиперболическими:
синусом, косинусом,
тангенсом,
котангенсом.
называются, соответственно,гиперболическими:
синусом, косинусом,
тангенсом,
котангенсом.
Если
задан график
![]() функции
функции![]() ,
,![]() ,
то построение графика функции
,
то построение графика функции![]() сводится к ряду преобразований (сдвиг,
сжатие или растяжение, отображение)
графика
сводится к ряду преобразований (сдвиг,
сжатие или растяжение, отображение)
графика![]() :
:
1)
преобразование
![]() симметрично отображает график
симметрично отображает график![]() ,
относительно оси
,
относительно оси![]() ;2)
преобразование
;2)
преобразование
![]() симметрично отображает график
симметрично отображает график![]() ,
относительно оси
,
относительно оси![]() ;3)
преобразование
;3)
преобразование
![]() сдвигает график
сдвигает график![]() по оси
по оси![]() на
на![]() единиц (
единиц (![]() -
вправо,
-
вправо,![]() - влево);4)
преобразование
- влево);4)
преобразование
![]() сдвигает график
сдвигает график![]() по оси
по оси![]() на
на![]() единиц (
единиц (![]() -
вверх,
-
вверх,![]() - вниз);5)
преобразование
- вниз);5)
преобразование
![]() график
график![]() вдоль оси
вдоль оси![]() растягивает в
растягивает в![]() раз, если
раз, если![]() или сжимает в
или сжимает в![]() раз, если
раз, если![]() ;6)
преобразование
;6)
преобразование
![]() график
график![]() вдоль оси
вдоль оси![]() сжимает в
сжимает в![]() раз, если
раз, если![]() или растягивает в
или растягивает в![]() раз, если
раз, если![]() .
.
Последовательность
преобразований при построении графика
функции
![]() можно представить символически в виде:
можно представить символически в виде:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Примечание.
При выполнении преобразования
![]()
![]() следует иметь в виду, что величина сдвига
вдоль оси
следует иметь в виду, что величина сдвига
вдоль оси![]() определяется той константой, которая
прибавляется непосредственно к аргументу
определяется той константой, которая
прибавляется непосредственно к аргументу![]() ,
а не к аргументу
,
а не к аргументу![]() .
.
Графиком
функции
![]() является парабола с вершиной в точке
является парабола с вершиной в точке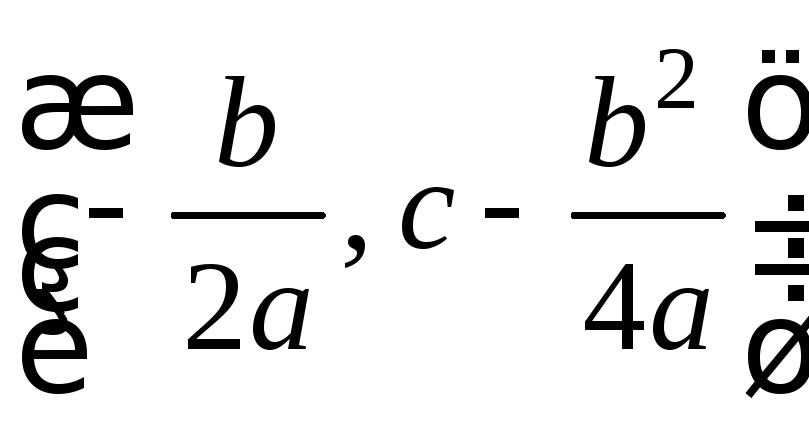 ,
ветви которой направлены вверх, если
,
ветви которой направлены вверх, если![]() или вниз, если
или вниз, если![]() .
Графиком дробно-линейной функции
.
Графиком дробно-линейной функции![]() является гипербола с центром в точке
является гипербола с центром в точке![]() ,
асимптоты которой проходят через центр,
параллельно осям координат.
,
асимптоты которой проходят через центр,
параллельно осям координат.
В
некоторых случаях при построении графика
функции целесообразно разбить её область
определения на несколько непересекающихся
промежутков и последовательно строить
график на каждом из них. Например, при
построении графика функции, в аналитическое
выражение которой входит функция
![]() ,
следует выделить и рассмотреть отдельно
промежутки, на которых выражение под
знаком модуля не меняет знак.
,
следует выделить и рассмотреть отдельно
промежутки, на которых выражение под
знаком модуля не меняет знак.
График
функции
![]() можно построить, предварительно построив
графики функций
можно построить, предварительно построив
графики функций![]() и
и![]() ,
а затем сложив их ординаты при одинаковых
значениях
,
а затем сложив их ординаты при одинаковых
значениях![]() .
.
В задачах 4.55-4.59 построить графики элементарных функций:
4.55
a)![]() ;б)
;б)![]() ;в)
;в)![]() ;г)
;г)![]() .
.
4.56
a)![]() ;б)
;б)![]() ;
;
в)
![]()
4.57
а)![]() ;б)
;б)![]() ;
;
в)
![]()
4.58
а)
![]() ;б)
;б)
![]() ;
в)
;
в)
![]() .
.
4.59
а)![]() ;б)
;б)![]() ;
в)
;
в)![]() .
.
4.60
Построить
графики следующих элементарных функций,
используя правило построения графика
функции
![]() по графику
по графику![]() :
:
а)
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ;
;
б)
![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ;
;
в)
![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() .
.
г)
![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() .
.
В задачах 4.61-4.64 построить графики дробно-линейных функций:
4.61
![]() .
4.62
.
4.62
![]() .
.
4.63
![]() .
4.64
.
4.64
![]() .
.
В задачах 4.65-4.81 построить графики следующих функций:
4.65![]() .4.66
.4.66
![]() .4.67
.4.67
![]() .
.
4.68![]() 4.69
4.69![]() .4.70
.4.70![]() .
.
4.71![]() .4.72
.4.72![]() .4.73
.4.73![]() .
.
4.74![]() 4.75
4.75![]() 4.76
4.76![]() .
.
