13.86 13.87

13.88 13.89

В задачах 13.90-13.93, предполагая, что выборки получены из двумерных нормально распределённых генеральных совокупностей, проверить гипотезу при альтернативной гипотезепо следующим данным:

13.90 13.91

13.92 13.93

Количественной характеристикой степени нелинейной зависимости между величинами иявляетсякорреляционное отношение ,. Равенствовлечёт независимость случайных величини, а равенствоимеет место тогда и только тогда, когдаисвязаны функциональной зависимостью. Состоятельной оценкой корреляционного отношения служит статистика, значение которой , в предположении, что выборка получена из двумерной генеральной совокупности (,) и представлена в виде корреляционной таблицы,,, вычисляется по формулам:,,,,.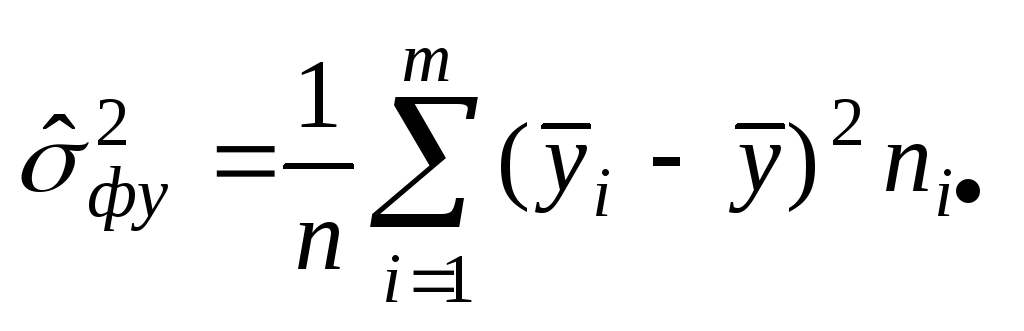

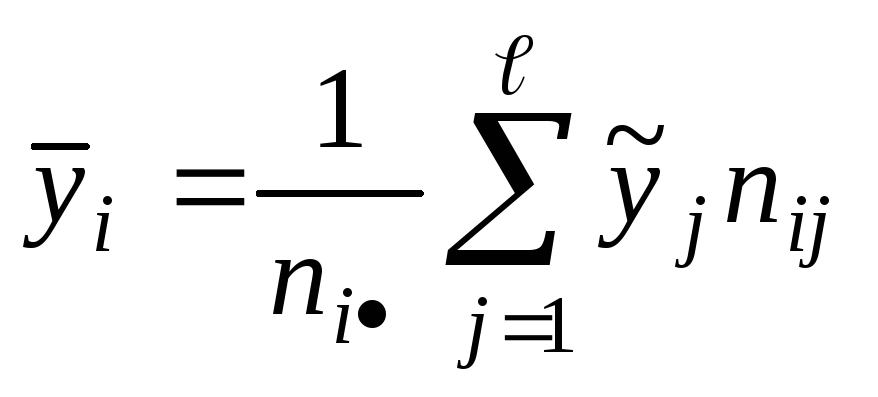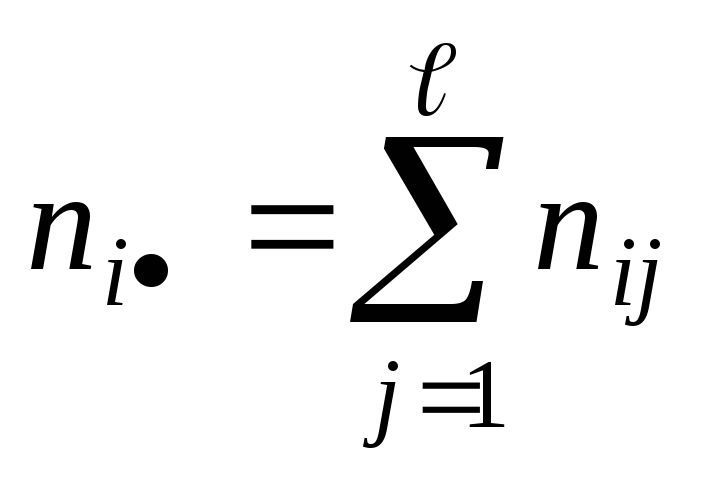Проверка гипотезы о значимости выборочного значения корреляционного отношения .

Гипотеза	Статистика критерия	Критическое множество
		, где ,,

Здесь: - критическая точка распределения Фишера (приложение 6.5а,б).

В задачах 13.94-13.95 вычислить эмпирическое корреляционное отношение и проверить гипотезупри альтернативной гипотезена уровне значимостипо следующим данным:

13.94

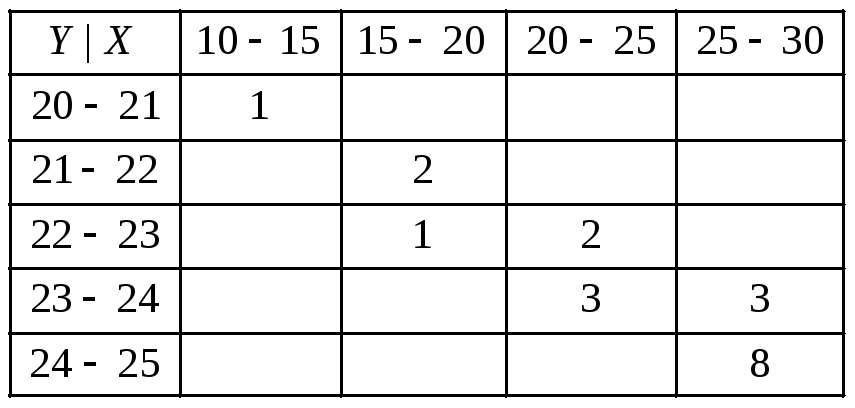
13.95

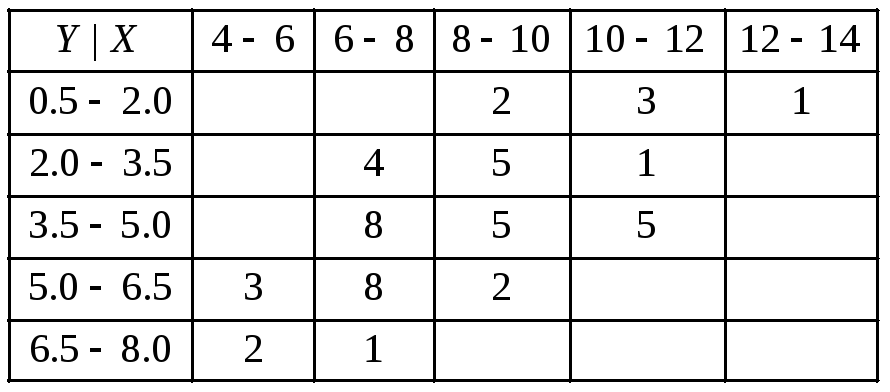
В задачах 13.96-13.97 требуется: а) вычислить эмпирическое корреляционное отношение и проверить его значимость на уровне;б) найти выборочное уравнение нелинейной регрессии , считая, что регрессионная зависимость между величинами и имеет вид. (Указание. Эмпирические коэффициенты ,,регрессионной зависимости находят как решение системы уравнений метода наименьших квадратов, где).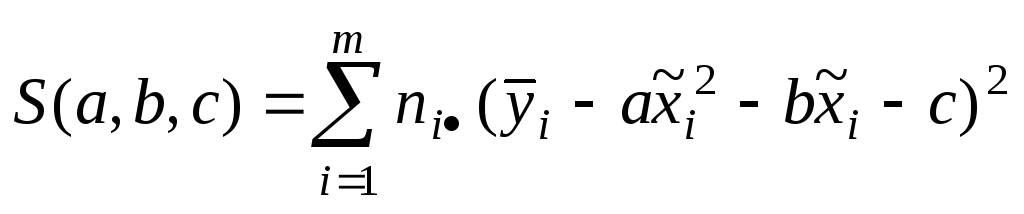

13.96 13.97

88