
- •Глава 13. Математическая статистика.
- •§1. Выборка, способы её записи, графическое представление и числовые характеристики.
- •13.9 13.10
- •Основные числовые характеристики выборки.
- •§2. Статистические оценки параметров распределения.
- •2.1 Точечные оценки.
- •2.2 Интервальные оценки. Необходимый объём выборки.
- •Доверительные интервалы для параметров инормально распределённой генеральной совокупности.
- •Доверительный интервал для параметра биномиального распределения.
- •§3. Проверка статистических гипотез.
- •3.1 Проверка гипотез о параметрах нормально распределённой генеральной совокупности. Проверка гипотез о средних нормального распределения.
- •3.2 Проверка гипотез о параметре биномиального распределения.
- •3.3 Проверка гипотезы о виде распределения генеральной совокупности.
- •§4. Корреляционно-регрессионный анализ.
- •13.80 13.81
- •13.86 13.87
- •13.88 13.89
- •13.90 13.91
- •13.92 13.93
- •13.96 13.97
§4. Корреляционно-регрессионный анализ.
На практике часто бывает важно знать, существует ли зависимость между некоторыми наблюдаемыми величинами, насколько тесно они связаны между собой, можно ли по значению одной величины сделать какие-либо выводы о предполагаемом значении другой величины и т.д. Для решения задач такого рода и применяется корреляционно-регрессионный анализ.
Пусть
![]() - выборка из двумерной генеральной
совокупности
- выборка из двумерной генеральной
совокупности![]() .
Предварительное представление о
зависимости между случайными величинами
.
Предварительное представление о
зависимости между случайными величинами![]() и
и![]() можно получить изобразив в прямоугольной
системе координат на плоскости точки
можно получить изобразив в прямоугольной
системе координат на плоскости точки![]() .
Такое графическое представление
двумерной выборки называютдиаграммой
рассеивания
(корреляционным
полем).
.
Такое графическое представление
двумерной выборки называютдиаграммой
рассеивания
(корреляционным
полем).
Количественной
характеристикой степени линейной
зависимости между величинами
![]() и
и![]() являетсякоэффициент
корреляции
являетсякоэффициент
корреляции
![]() .
Состоятельной оценкой коэффициента
корреляции служит статистика
.
Состоятельной оценкой коэффициента
корреляции служит статистика![]() ,
где
,
где![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
Если
![]() ,
то все выборочные точки
,
то все выборочные точки![]() ,
,![]() лежат на одной прямой. При
лежат на одной прямой. При![]() выборочные данные только имеют тенденцию
сосредотачиваться около прямых:
выборочные данные только имеют тенденцию
сосредотачиваться около прямых:
![]() ,
,
![]() ,
,
называемых
(теоретическими)
прямыми
регрессии
![]() на
на![]() и
и![]() на
на![]() ,
соответственно. Здесь
,
соответственно. Здесь![]() ,
,![]() .
Первое уравнение даёт наилучший в
среднем квадратичном прогноз ожидаемых
значений
.
Первое уравнение даёт наилучший в
среднем квадратичном прогноз ожидаемых
значений![]() по наблюдениям
по наблюдениям![]() ,
второе – прогноз значений
,
второе – прогноз значений![]() по наблюдениям
по наблюдениям![]() .
.
Прямые
![]() ,
,![]() называютсяэмпирическими
прямыми регрессии
называютсяэмпирическими
прямыми регрессии
![]() на
на![]() и
и![]() на
на![]() ,
соответственно. Здесь
,
соответственно. Здесь
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() -
найденные по выборке
-
найденные по выборке![]() ,
,![]() ,
значения статистик
,
значения статистик![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
являющихся состоятельными оценками
параметров
,
являющихся состоятельными оценками
параметров![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() двумерной генеральной совокупности.
Если выборка представлена корреляционной
таблицей
двумерной генеральной совокупности.
Если выборка представлена корреляционной
таблицей![]() ,
,![]() ,
,![]() ,
,![]() ,
где
,
где![]() ,
,![]() - или отдельные различные выборочные
значения
- или отдельные различные выборочные
значения![]() и
и![]() или середины интервалов группировки
выборочных значений
или середины интервалов группировки
выборочных значений![]() и
и![]() ,
,![]() - частота с которой в выборке встречается
пара
- частота с которой в выборке встречается
пара![]() ,
то значения статистик вычисляются по
формулам:
,
то значения статистик вычисляются по
формулам:
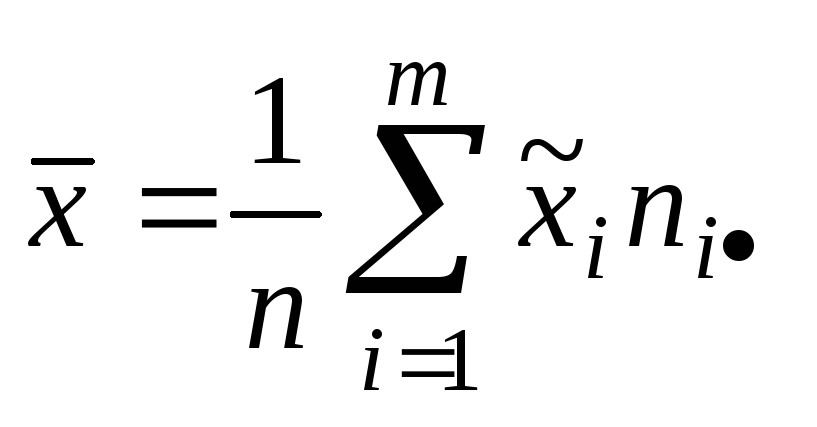 ,
,
![]() ,
,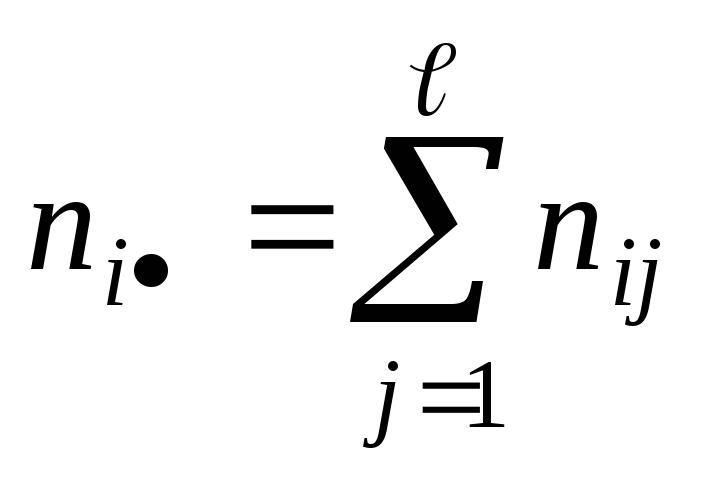 ,
,![]() ,
,
![]() ,
,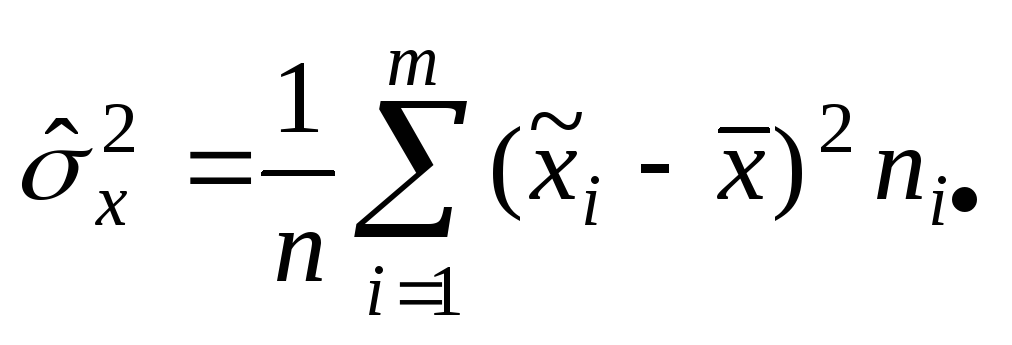 ,
,![]()
В задачах
13.80-13.81 для
указанных выборок вычислить коэффициенты
корреляции
![]() и построить
диаграммы рассеивания.
и построить
диаграммы рассеивания.
13.80 13.81
В задачах
13.82-13.83 для
указанных выборок вычислить коэффициенты
корреляции, определить и нанести на
диаграмму рассеивания прямые регрессии
![]() и
и![]() .
.
13.82
![]()
13.83![]()
![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
![]()
В задачах
13.84-13.85 вычислить
коэффициент корреляции и найти уравнения
прямых регрессии
![]() и
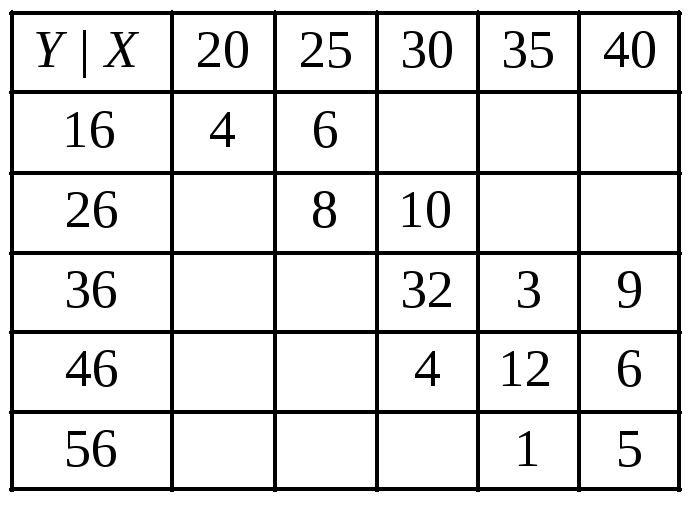
и![]() по данным в следующих корреляционных
таблицах:
по данным в следующих корреляционных
таблицах:
13.84
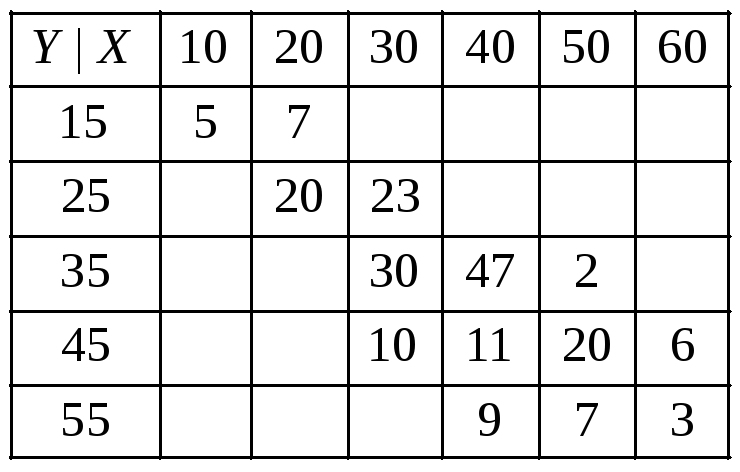
13.85
В случае выбора
из двумерной нормально распределённой
генеральной совокупности равенство
![]() влечёт независимость случайных величин
влечёт независимость случайных величин![]() и
и![]() .
Проверка параметрической гипотезы
.
Проверка параметрической гипотезы![]() основана на статистике
основана на статистике![]() ,
которая имеет распределение Стьюдента
с
,
которая имеет распределение Стьюдента
с![]() степенями свободы.
степенями свободы.
Проверка гипотезы о значимости выборочного коэффициента
корреляции
![]() .
.
|
Гипотеза
|
Статистика критерия |
Критическое множество |
|
|
|
где
|
Здесь:
![]() -критическая точка распределения
Стьюдента (приложение 6.4),
-критическая точка распределения
Стьюдента (приложение 6.4),![]() .-
объём выборки.
.-
объём выборки.
Доверительный
интервал для коэффициента корреляции![]() .
.
![]()
Здесь:
![]() - корень уравнения
- корень уравнения
![]() (приложение.6.2);
(приложение.6.2);
![]() -выборочный коэффициент корреляции;
-выборочный коэффициент корреляции;![]() -
объём выборки. Значения гиперболического
тангенса вычисляются по таблице
приложения 6.6.
-
объём выборки. Значения гиперболического
тангенса вычисляются по таблице
приложения 6.6.
В задачах
13.86-13.89 построить
доверительные интервалы для коэффициентов
корреляции
![]() двумерной нормально распределённой
генеральной совокупности по следующим
данным:
двумерной нормально распределённой
генеральной совокупности по следующим
данным:
