Bilety_integraly (1) / 1_11

№11

Теорема о среднем

Пусть функции   и   удовлетворяют следующим условиям:

1. 

2. 

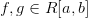
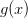3.  не меняет знак на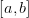 

Тогда

.

Доказательство

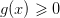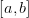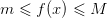Не ограничивая общности рассуждений рассмотрим случай   на  . Домножив все части неравенства   на  , получим

.

По свойству монотонности интеграла, получим

.

Если  , то и  , тогда   — любое изотрезка  . Пусть, далее,  . Разделим все части неравенства на 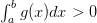 , будем иметь

.

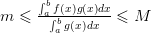Обозначим

.

Получили, что   и  . Случай   доказывается аналогично.