
Электродинамика и распространение радиоволн
..pdf
2.9. Энергия электростатического поля
Нам уже известно выражение для энергии электрического поля:
|
εE |
2 |
( |
|
, |
|
) |
|
W = |
E |
D |
|
|||||
|
= |
|
|
|
|
|
. |
|
|
|
|
|
|
|
|||
э |
2 |
|
2 |
|
|
|
||
|
|
|
|
|
||||
Выразим энергию электростатического поля через потенциал и объемную плотность заряда:
Wэ = 12 V∫EDdv = −12 V∫D grad ϕdv ; div(ϕD)= ϕdiv D + Dgrad ϕ;
Wэ = 12 V∫ϕdiv Ddv − 12 V∫div(ϕD)dv.
Рассмотрим второй интеграл в последнем выражении. Применим к нему теорему Остроградского – Гаусса:
∫div(ϕ |
|
)dV |
= ∫ϕ |
|
|
|
|
|
|
|
|
|
|||
D |
DdS . |
||||||
V |
S |
||||||
Интересуясь всей энергией, создаваемой системой электрических зарядов, распространим интегрирование на все исследуемое пространство. Другими словами, окружим область, в которой имеются заряды, условной сферической поверхностью и устремим ее радиус в бесконечность. Так как произведение ϕD убывает быст-
рее, чем r−2 , а площадь сферы увеличивается как r2 , исследуемый интеграл обращается в ноль. Следовательно, формула для энергии электростатического поля имеет вид
Wэ = 12 V∫ϕ ρdV .
В последнем соотношении учтено, что div D = ρ.
71

Контрольные вопросы
1.Охарактеризуйте понятие «электростатическое поле».
2.Получите уравнения электростатического поля из уравнений Максвелла.
3.Какой физический смысл придается электростатическому потенциалу ϕ?
4.Какая интегральная и дифференциальная связь существует между E и ϕ?
5.Поясните физическое содержание вектора Пойнтинга.
6.Изменяются ли при переходе через границу раздела двух
сред с различными ε полные значения E и D ?
7.Запишите граничные условия для векторов электрического поля при переходе через границу «идеальный диэлектрик – проводник».
8.Охарактеризуйте виды распределения зарядов.
9.Получите из уравнений Максвелла для электрического поля уравнения для потенциала.
10.Сформулируйте основную задачу электростатики.
11.Сформулируйте теорему единственности.
12.Перечислите основные методы решения задач электроста-
тики.
13.Дайте обоснование методу зеркальных изображений.
72

3.Электромагнитное поле постоянных токов
3.1. Электрическое поле постоянного тока
Электрическое поле постоянного тока подобно полю электростатическому потенциально. Однако на проводящих границах потенциал уже не постоянен и вектор Е не составляет с ними прямого угла. Таким образом, электрическое поле системы проводящих тел, несущих ток, отличается от электростатического поля этой же системы.
Посмотрим, насколько велико может быть на практике отмеченное различие. Пусть разность потенциалов двух параллельных
токонесущих пластин из меди (σ = 5,8 107 См м), лежащих на расстоянии d = 1 см, составляет ϕB −ϕA =10 В, а плотность тока j = 2 А/мм2 .
м), лежащих на расстоянии d = 1 см, составляет ϕB −ϕA =10 В, а плотность тока j = 2 А/мм2 .
Вычислим компоненты вектора Е у поверхности проводника: тангенциальная
Eτ = σj ≈ 3,5 10−2 В/м;
нормальная
En = ϕB −ϕA =103 В/м. d
Как видно, их отношение оказывается весьма малой величиной:
Eτ 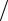 En = 3,5 10−5 ,
En = 3,5 10−5 ,
и электрическое поле практически нормально токонесущему проводнику. По виду оно пренебрежимо мало отличается от поля электростатического конденсатора, образованного взятыми пластинами. Рассмотренный пример типичен. Тангенциальная компонента вектора Е на проводящей токонесущей поверхности обычно
73

настолько мала, что отличие электрического поля в диэлектрике от электростатического оказывается несущественным.
Иное наблюдается внутри проводника. Как известно, электростатическое поле там всегда отсутствует. Но при наличии постоянного тока в проводящей среде существует электрическое поле, описываемое уравнениями
rot |
|
|
= 0, |
|
|
|||||
E |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
j = σE, |
(3.1) |
||||||||
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
div j = 0; |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Edl = 0, |
|
||||||
|
|
||||||
L |
|
|
|
|
|
|
(3.2) |
∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j |
|
ds |
= 0. |
|
|
S |
|
|
|
|
|
|
|
Последнее из уравнений (3.1) есть не что иное, как уравнение закона сохранения заряда, записанное для стационарного процесса (∂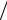 ∂t = 0). Оно выражает непрерывность линий постоянного тока.
∂t = 0). Оно выражает непрерывность линий постоянного тока.
Сопоставляя систему уравнений (3.1) с уравнениями электростатического поля в среде, не содержащей зарядов:
rot |
|
|
= 0, |
|
|
|||||||||||
E |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D = εE, |
|
(3.3) |
||||||||||||||
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
= |
|
|
|
||||
div |
D |
0; |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫ |
|
|
|
|
|
0, |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Edl = |
|
|||||||||||||||
L |
|
|
|
|||||||||||||
|
|
(3.3а) |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫ Dds = |
|
|
||||||||||||||
0, |
|
|||||||||||||||
S |
|
|
|
|||||||||||||
видим, что они совершенно одинаковы по форме. Уравнения электростатики (3.3) становятся справедливыми для электрического поля в проводящей среде, если электрическую индукцию D заменить в них на плотность тока j , а диэлектрическую проницаемость ε —
74

удельной проводимостью σ. На этом основании говорят, что между обоими полями существует формальная аналогия.
В ряде случаев указанное обстоятельство помогает нахождению электрического поля в проводящей среде. Если в рассматриваемой задаче все граничные поверхности имеют ту же форму, что и в некоторой электростатической задаче, и вектор j ведет себя в
первом случае на границах так же, как вектор D во втором, то можно использовать готовое решение электростатической задачи, сделав в нем замену
|
|
на |
|
и ε на σ. |
(3.4) |
|
D |
j |
Так, вектор j в слабо проводящей среде нормален ограничивающей ее поверхности хорошего проводника. Действительно, это вытекает из второго уравнения (3.2)
∫ j dS = 0.
S
Нормальная составляющая j на границе сред непрерывна:
|
|
|
|
|
|
(3.5) |
|
j1n = j2n , |
|
||||
а тангенциальная составляющая |
в |
силу |
непрерывности Еτ |
|||
(Е1τ = Е2τ ) подчинена соотношению |
|
|
||||
j |
= j |
σ1 |
, |
(3.6) |
||
|
||||||
1τ |
1τ σ |
|
|
|||
|
|
|
|
2 |
|
|
т.е. в слабо проводящей среде она в σ1 раз меньше, чем в хорошем
σ2
проводнике. При достаточном различии проводимостей σ1 и σ2 составляющей j1τ можно пренебречь и считать вектор j1 нормальным
границе.
Если заменить слабо проводящую среду идеальным диэлектриком, то можно рассмотреть электростатическую задачу, в которой вектор D будет также нормальным границе. Пусть решение электростатической задачи известно заранее. Тогда, сделав в нем замену (3.4), мы получаем поле в слабо проводящей среде.
75
На принципе отмеченной выше аналогии базируется также моделирование электростатических полей в электролитической ванне. Для экспериментального исследования электростатического поля системы проводящих тел последние помещают в ванну и, создав требуемые потенциалы, измеряют плотность тока в различных участках электролита. Найденное таким путем поле тока в электролите представляет собой модель электростатического поля системы. Гарантией этому служит значительное различие удельных проводимостей электролита и элементов системы (обычно металлических), позволяющее считать, что вектор плотности тока к поверхностям системы нормален.
3.2. Магнитное поле постоянного тока
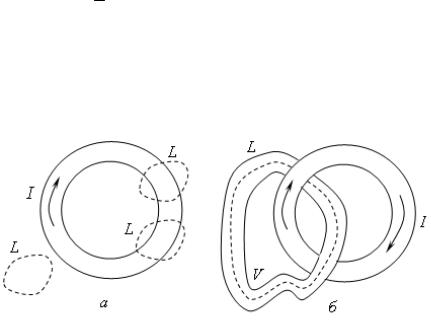
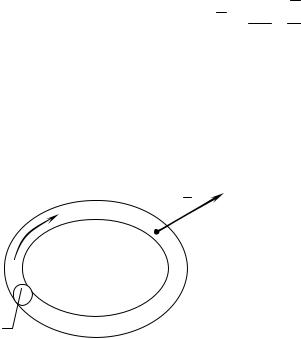
В этом подразделе мы ограничимся наиболее простыми проявлениями магнитного поля. Будем рассматривать лишь области, не содержащие тока ( j = 0). Поставим также условие, чтобы любой мыслимый контур в области не охватывал тока (рис. 3.1,а). Кольцевые области, подобные изображенной на рис. 3.1,б, охватывающие ток, пока исключаются из анализа.
Рис. 3.1. Контур L не охватывает виток
спостоянным током (а); контур L охватывает виток
спостоянным током (б)
Тогда из уравнений Максвелла выделится независимая система уравнений магнитостатики:
76

|
|
|
|
|
|
|
|
= 0, |
|
|
||||
|
rot H |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
div B = 0, |
(3.7) |
||||||||||||
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
B |
|
= μH |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫ H dl = 0, |
|
||||||||||||
|
L |
|
|
|
|
|
|
|
|
|
|
(3.8) |
||
|
∫ |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
Bds = 0. |
|
||||||||
|
S |
|
|
|
|
|
|
|
|
|
|
|
||
Первое из дифференциальных уравнений позволяет немедлен- |
||||||||||||||
но записать |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
= −grad ϕм, |
(3.9) |
|||||||||||
H |
||||||||||||||
где ϕм — магнитостатический потенциал.
Из (3.7) следует, что магнитостатический потенциал подчиня-
ется уравнению Лапласа: |
|
|
|
|
|
|
|
|
|
|
|
|
|
2ϕм = 0. |
|
(3.10) |
|||||||||
|
|
|
||||||||||
Принимая во внимание, что граничные условия для вектора H |
|
|||||||||||
H |
1τ |
= H |
2τ |
, |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
(3.11) |
|||||
μ |
H |
|
= μ |
|
|
H |
|
|
||||
1n |
2 |
|
|
|
|
|
||||||
1 |
|
|
|
2n |
|
|
|
|||||
ничем не отличаются от таких же условий для вектора Е , приходим к очевидному выводу, что решения задач магнитостатики формально идентичны решениям соответствующих электростатических задач и могут быть получены из них простой заменой величин E на H и ε на μ.
Продолжим изучение магнитного поля постоянного тока, отказавшись от поставленных выше ограничений. С этой целью запишем в полном виде уравнения Максвелла, относящиеся к магнит-
ному полю, при условии |
∂ |
= 0 : |
|
|
|
|
|
∂t |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(3.12) |
|
|
rot H |
= |
j |
, |
||
77
div |
|
= 0, |
(3.13) |
||||
B |
|||||||
∫ Hdl = I , |
(3.14) |
||||||
l |
|
||||||
∫ Bd s = 0 . |
(3.15) |
||||||
S |
|
||||||
Добавим сюда материальное уравнение |
|
||||||
|
|
|
|
. |
(3.16) |
||
B |
= μ H |
||||||
Сосредоточим внимание на связи магнитного поля и постоянного тока. Покажем, что однозначную связь между потенциалом
магнитного поля ϕм и полем установить не удается. Пусть задан контур с током (рис. 3.2).
Рис. 3.2. К определению разности магнитных потенциалов между точками A и B
Определим разность магнитных потенциалов между точками A и B. При этом от точки A до точки B будем проходить разными путями:
ΔϕмAmB = ΔϕмA − ΔϕмB ;
ϕмAnB = ΔϕмA − ΔϕмB + I; ΔϕмAlB = ΔϕмA − ΔϕмВ + 2I.
78
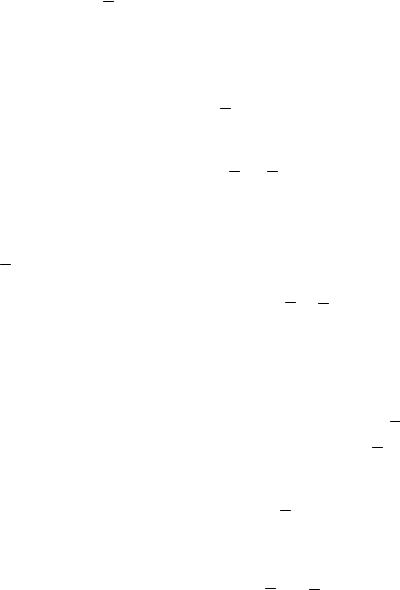
Отсюда видно, что разность потенциалов зависит от формы пути, следовательно, скалярный потенциал в области, содержащей токи, не может определять поле.
С целью установления связи между полем и вызывающим его током введем векторный магнитный потенциал, удовлетворяющий уравнениям (3.12), (3.13):
div |
|
= 0 |
|
|
|
|
|
|
|
||
B |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B = rot A. |
(3.17) |
|||||
|
|
|
|
|
|
||||||
div rot |
A |
≡ 0 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
Вектор A называется векторным магнитным потенциалом. Сам он определяет поле неоднозначно, так как
B = rot |
|
= rot ( |
|
+ grad ϕ). |
(3.18) |
A |
A |
Действительно, если A есть решение (3.18), то решением будет также функция
А′ = А+ grad ϕ,
где ϕ — некоторый скаляр.
Из уравнений Максвелла выведем уравнения для потенциала A. Подставляя (3.17) в (3.12) с учетом (3.16), получим
rot rot A = jμ.
Воспользовавшись формулой векторного анализа, запишем:
grad div |
|
− 2 |
|
= |
|
μ. |
(3.19) |
|
A |
A |
|||||||
j |
Из (3.18) следует, что в выборе вектора A допускается известный произвол. В связи с этим наложим на A дополнительное условие, называемое «кулоновской калибровкой»:
div A = 0. |
|
Тогда (3.19) принимает вид |
|
2 A = − jμ. |
(3.20) |
79
Это векторное уравнение соответствует трем скалярным:
2 Ax = − jxμ;
2 Ay = − jyμ;
2 Az = − jzμ.
Сравним результат с уравнением Пуассона для электростатиче-
ского потенциала. Запишем его еще раз: 2ϕ = −ρε . Решение этого
уравнения имеет вид ϕ = |
1 |
∫ |
ρ dv. |
|
|
|
|
|
|
|
|
|
||||||
4πε |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
V |
r |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Отсюда запишем проекции вектора |
|
: |
|
|
|
|
|
|||||||||||
А |
|
|
|
|
|
|||||||||||||
A = |
μ |
|
jx |
dv; |
A = |
|
μ |
|
jy |
dv; |
A = |
μ |
|
jz |
dv. |
|||
|
|
|
|
|
|
|||||||||||||
x |
4π ∫ r |
y |
|
|
4π ∫ |
r |
z |
4π ∫ |
r |
|||||||||
|
|
V |
|
|
|
|
V |
|
|
|
|
|
|
V |
|
|
||
Зная проекции, найдем вектор:
A = 4μπV∫ rj dv.
3.3. Магнитное поле линейного тока
М
I |
r |
S
Рис. 3.3. К вопросу определения магнитного поля линейного тока
Воспользуемся выражением для векторного магнитного потенциала, чтобы найти магнитное поле в наиболее важном случае линейного тока.
Пусть это будет ток, протекающий в замкнутом контуре L произвольной формы (рис. 3.3). Площадь его поперечного сечения S .
80
