
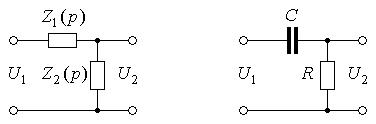
Практическое занятие № 1
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ И ПЕРЕДАТОЧНЫЕ ФУНКЦИИ ЗВЕНЬЕВ И СИСТЕМ
Задача 1. Найти передаточную функцию и дифференциальное уравнение пассивной электрической цепи относительно напряжений
U1 |
и U 2 |
(рис. 1, а). |
а |
б |
|
Рис. 1 |
Решение. Для нахождения передаточных функций электрических цепей, подобных изображенной на рис. 1, а, удобно воспользоваться операторной формой записи сопротивлений: индуктивного – Z ( p) = pL , емкостного – Z ( p) = 1/ pC и активного – Z ( p) = R , где
p = d / dt
оператор дифференцирования.
Так как падение напряжения на последовательно соединенных сопротивлениях пропорционально величине сопротивлений, то передаточная функция рассмотренной цепи (рис. 1, а) находится как отношение выходного и входного сопротивлений. При этом
Z |
вх |
( p) = Z |
1 |
( p) + Z |
2 |
( p) |
; |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Z |
вых |
( p) = Z |
2 |
( p) |
. |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
W ( p) = |
U 2 |
= |
|
Zвых ( p) |
= |
|
Z2 ( p) |
. |
||||||||||
|
|
|
|
|||||||||||||||
|
|
|
|
U1 |
|
|
|
|
|
Zвх ( p) |
|
|
Z1 |
( p) + Z2 ( p) |
|
|||
Дифференциальное уравнение рассматриваемой электрической цепи относительно напряжений имеет вид
[Z1( p) + Z2 ( p)]U 2 = Z2 ( p)U1 .
Например, для звена, изображенного на рис. 1, б получаем:
1
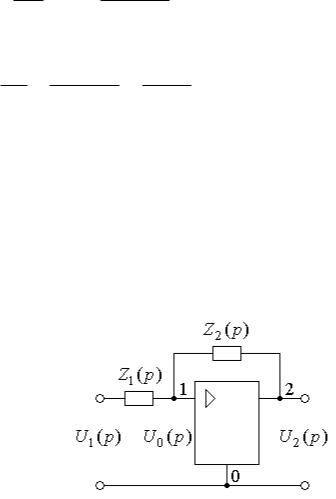
где
Zвх ( p) = |
1 |
+ R = |
1 + pRC |
; |
|
||||
pC |
|
pC |
|
||||||
|
|
|
|
|
|
||||
Zвых ( p) = R ; |
|
|
|
|
|
|
|||
W ( p) = |
U |
2 |
= |
pRC |
= |
Tp |
; |
||
|
|
|
|
|
|||||
U |
|
1 + pRC |
Tp +1 |
||||||
|
1 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
(Tp +1)U 2 |
= TpU 1 , |
|
|
|
|
|
|||
T = RC – постоянная времени. |
|
||||||||
Данное звено является реальным дифференцирующим звеном.
Задача 2. Вывести уравнение динамики и определить передаточную функцию аналогового вычислительного устройства на основе операционного усилителя (рис. 2).
Рис. 2
Решение. сопротивление
напряжение
U
Усилитель предполагается идеальным: его входное между зажимами 1–0 бесконечно велико, а выходное 2 не зависит от нагрузки. Последнее означает, что
внутреннее сопротивление усилителя между зажимами 2–0 принимается равным нулю.
Для узла 1 справедливо следующее соотношение токов
|
I1 = I2 + Iоу . |
|||
Так как операционный усилитель имеет большое входное сопро- |
||||
тивление, то Iоу = 0 . Тогда |
||||
|
I1 = I2 |
|
|
|
или |
|
|
|
|
|
U1 −U 0 |
= |
U 0 −U 2 |
. |
|
|
|||
|
Z1( p) |
|
Z2 ( p) |
|
2

где
Напряжение на выходе операционного усилителя kоу – коэффициент усиления. Тогда U0 = U2 / kоу .
U2
=
k |
U |
0 |
|
оу |
,
Так как коэффициент операционного усилителя достаточно большой (он обычно достигает тысяч и десятков тысяч), то kоу → и
U0
→ 0 . При этом получим
Z2 ( p)U1 = −Z1( p)U 2 .
Следовательно, дифференциальное уравнение имеет вид
Z1( p)U 2 = −Z2 ( p)U1 .
Передаточная функция
W ( p) = |
U |
2 |
= − |
Z |
2 |
( p) |
. |
|
|
|
|||||
U |
|
Z |
( p) |
||||
|
1 |
|
|
||||
|
|
|
|
1 |
|
|
|
Выбирая различные значения
Z |
1 |
( p) |
|
|
и
Z |
2 |
( |
|
|
p)
, на основании по-
следнего выражения можно получить модели различных звеньев.
|
|
Например, используя в качестве сопротивлений |
Z1( p) |
и Z 2 ( p) |
||||||||
активные сопротивления |
1 и |
R |
2 , построим пропорциональное звено |
|||||||||
с |
|
|
|
R |
|
2 |
1. Выбирая |
|
1 |
|
1 , а |
|
|
коэффициентом передачи |
|
|
|
|
|||||||
|
2 |
|
|
|
k = −R |
|
/ R |
Z |
|
( p) = R |
||
Z |
( p) = 1/ pC |
, получим интегрирующее звено с передаточной функ- |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
||
цией W ( p) = −1/ Tp , где |
T = R1C . Включая в качестве сопротивления |
|||||||||||
Z |
2 |
( p) |
|
|
параллельное соединение конденсатора емкостью
C
и рези-
стора сопротивлением ной функцией W ( p) =
R −k
2 , построим инерционное звено с передаточ-
/(Tp +1), где k = R2 / R1 ; T = R2C .
Таким образом, можно получить модели различных типовых звеньев линейных систем автоматического управления.
Z1( p) || Z2 ( p) = Z1( p)+Z2 ( p) .
Z1( p) Z2 ( p)
Задача 3. Определить эквивалентную передаточную функцию следующего соединения звеньев:
3

Рис. 3
W12 ( p) = W1( p) +W2 ( p) ; |
|
|
|
|
|
|
|
|
|
||||||
W123 ( p) = [W1( p) + W2 ( p)]W3 ( p) ; |
|
|
|
||||||||||||
|
|
W |
( p) |
|
[W |
( p) +W |
( p)]W |
( p) |
|
||||||
Ф( p) = |
123 |
|
|
= |
1 |
|
|
|
|
2 |
3 |
|
|
= |
|
1 +W |
|
( p) |
1 + [W |
( p) +W ( p)]W |
( p) |
||||||||||
|
|
|
|
|
|||||||||||
|
|
123 |
|
|
|
1 |
|
|
|
2 |
3 |
|
|
||
|
W ( p)W ( p) +W |
( p)W |
|
( p) |
|
|
|
|
|
||||||
= |
1 |
3 |
|
|
2 |
3 |
|
|
|
. |
|
|
|
|
|
+W |
( p)W |
( p) +W ( p)W |
|
( p) |
|
|
|
|
|||||||
1 |
|
|
|
|
|
|
|||||||||
|
1 |
3 |
|
|
|
2 |
|
3 |
|
|
|
|
|
|
|
Задача 4. Определить эквивалентную передаточную функцию следующего соединения звеньев:
|
|
|
|
|
|
|
|
|
|
Рис. 4 |
|
|
Ф23 ( p) = |
|
W2 ( p) |
|
|
|
; |
|
|
||||
|
+W2 ( p)W3 |
|
|
|
|
|
||||||
|
1 |
( p) |
|
|
||||||||
W ( p) = W1( p)Ф23 ( p) = |
|
W1( p)W2 ( p) |
; |
|
||||||||
|
+W2 ( p)W3 ( p) |
|
||||||||||
|
|
|
|
|
|
|
1 |
|
|
|||
|
|
W ( p) |
|
|
|
W1( p)W2 ( p) |
||||||
Ф( p) = |
|
|
= |
|
. |
|||||||
1 +W ( p) |
1 +W1( p)W2 ( p) +W2 ( p)W3 ( p) |
|||||||||||
4
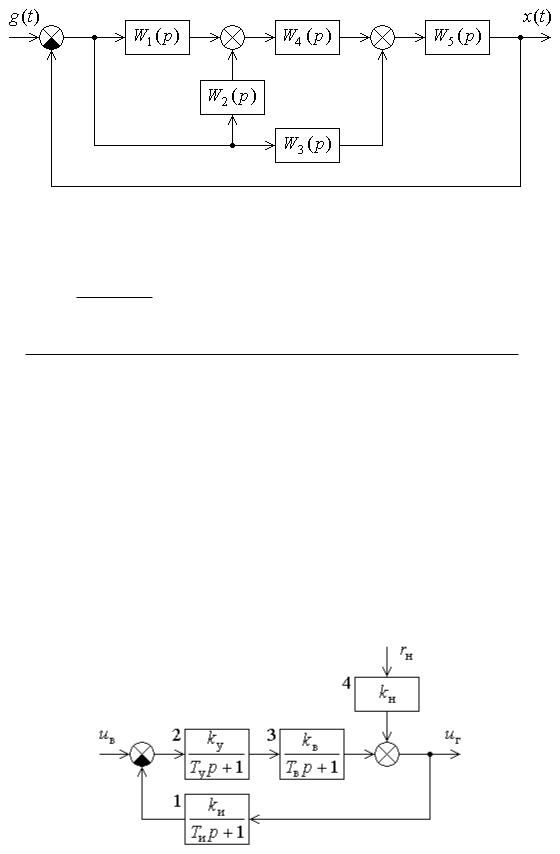
Задача 5. Найти передаточную функцию САУ, структурная схема которой приведена на рисунке.
Рис. 5
W ( Ф(
= 1
p) ={[W1( p) +W2 ( p)]W4 ( p) +W3 ( p)}W5 ( p) ; |
|
|
|
|
||||||||
p) = |
W ( p) |
= |
|
|
|
|
|
|
|
|
|
|
1 +W ( p) |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
||
W ( p)W ( p)W |
( p) +W |
( p)W |
( p)W |
( p) +W |
( pW |
( p) |
||||||
1 |
4 |
|
5 |
|
2 |
4 |
5 |
3 |
|
5 |
|
|
+W |
( p)W |
( p)W |
( p) +W ( p)W ( p)W ( p) +W |
( pW |
( p) |
|||||||
1 |
4 |
|
|
5 |
|
2 |
4 |
5 |
3 |
|
5 |
|
.
Задача 6. Необходимо написать выражения для передаточных функций системы автоматического регулирования напряжения синхронного генератора. Структурная схема системы приведена на рис 6. В схему входят три апериодических звена: звено 1 – измеритель напряжения, звено 2 – усилитель и звено 3 – генератор, являющийся объектом регулирования. В качестве внешних воздействий на схеме указаны изменение задающего воздействия uз , определяющего регу-
лируемое значение напряжения, и изменения активного сопротивле-
ния нагрузки |
н . |
|
r |
Рис. 6
5
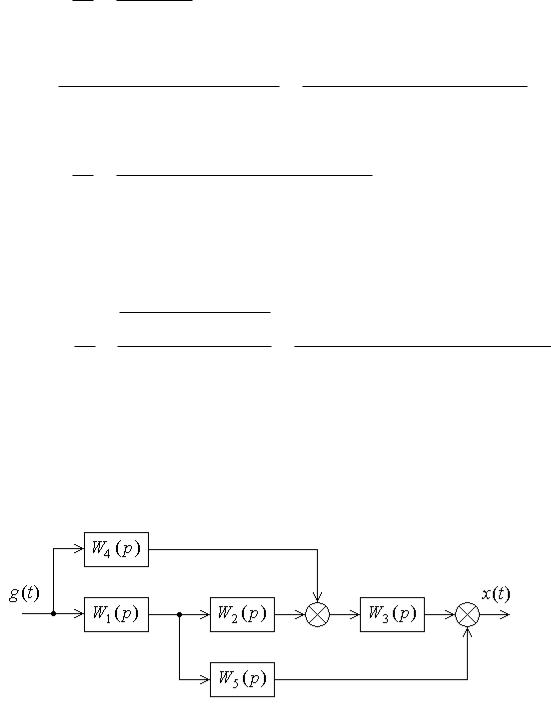
Решение. Согласно формуле (5.5), получаем передаточную функцию для возмущения
Ф |
r |
( p) |
|
н |
|
где
W ( p) =
=uг rн
(T |
p |
и |
|
=
+
k |
|
|
|
|
|
|
|
н |
, |
|
|
|
|
|
|
1 +W ( p) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
kиkуkв |
|
= |
|
k |
|
|
|
1)(T p +1)(T p +1) |
р +1)(T |
p +1)(Т |
|
p +1) |
|||
(T |
в |
||||||
в |
|
в |
и |
у |
|
|
|
После освобождения от дроби в знаменателе
|
|
|
u |
|
|
k |
н |
(T |
p +1)(T |
p +1)(Т |
в |
p +1) |
|||
Ф |
|
( p) = |
г |
= |
|
и |
|
у |
|
|
|
|
|||
r |
|
|
|
|
|
|
|
|
|
|
|
||||
r |
|
(T |
р +1)(T |
p +1)(Т |
|
p +1) + k |
|||||||||
|
н |
|
|
|
|
||||||||||
|
|
н |
|
|
и |
|
у |
|
|
в |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|||||
.
Если раскрыть скобки в числителе и знаменателе, получим многочлены третьего порядка.
Передаточная функция для задающего воздействия
k |
у |
k |
в |
|
|
Фu ( p) = u
зu
г з
|
(T |
p +1)(Т |
в |
p +1) |
= |
у |
|
|
|
|
1 +W ( p) |
|||
|
|
|||
=
|
k |
у |
k |
в |
(T |
p +1) |
||
|
|
|
и |
|
|
|
||
(T |
р +1)(T |
p +1)(Т |
в |
p +1) + k |
||||
и |
|
|
у |
|
|
|
|
|
.
Таким образом, числитель второй передаточной функции имеет первый порядок.
Задача 7. Найти передаточную функцию САУ, структурная схема которой приведена на рисунке.
Рис. 7
W ( p) =W4 ( p)W3 ( p) +W ( p)1W ( p)2W3 ( p) +W1( p)W5 ( p).
6
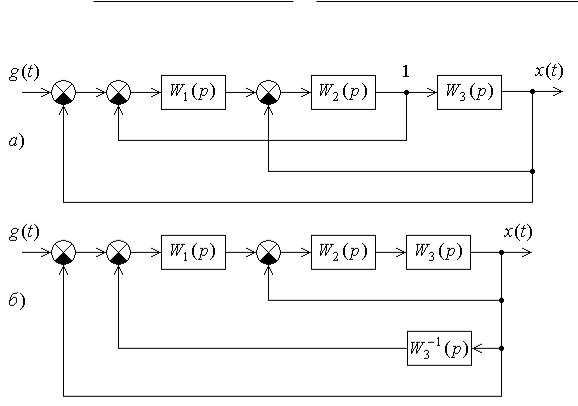
Задача 8. Найти передаточную функцию
Ф( p)
замкнутой авто-
матической системы управления, структурная схема которой изображена на рис. 8, а.
Решение. Освободимся от перекрестных связей в структурной схеме на рис. 8, а, для чего перенесем узел 1 через звено W3 ( p) по
направлению действия сигнала. При этом получаем систему с тремя вложенными друг в друга контурами обратной связи (рис. 8, б).
Передаточная функция внутреннего замкнутого контура:
Ф1 |
( p) = |
|
|
W2 ( p)W3 ( p) |
|
. |
|
|
|
|
|
|
|
|
|
|||
|
|
+W2 |
( p)W3 |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
1 |
( p) |
|
|
|
|
|
|
|
|
|
|||||
Передаточная функция второго замкнутого контура: |
|
|
||||||||||||||||
|
|
|
|
|
W ( p)Ф |
( p) |
|
|
|
W ( p)W |
( p)W |
( p) |
|
|||||
Ф |
|
( p) = |
|
|
|
1 |
1 |
|
|
|
|
= |
|
1 |
2 |
3 |
|
|
|
|
|
|
|
|
|
|
−1 |
|
|
|
|
|
|
|
|||
2 |
|
|
1 +W ( p)Ф |
( p)W |
( p) |
|
1 +W |
( p)W |
( p) +W ( p)W |
( p) |
||||||||
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
1 |
1 |
|
3 |
|
|
2 |
3 |
|
1 |
2 |
|
||
.
Рис. 8
Передаточная функция внешнего замкнутого контура:
Ф( p) = Ф3 |
( p) = |
|
Ф2 |
( p) |
= |
|
+ Ф2 ( p) |
||||
|
1 |
|
|||
|
W1( p)W2 ( p)W3 ( p) |
|
= |
|
. |
1 +W1( p)W2 ( p) +W2 ( p)W3 ( p) +W1( p)W2 ( p)W3 ( p) |
||
7

Задача 9. Дано дифференциальное уравнение динамического звена (системы управления):
2 |
d |
2 |
y(t) |
|
dy(t) |
|
|
|
du(t) |
|
|
|
|
|
|
+ T1 |
+ y(t) = K |
τ1 |
+ u(t) |
, |
|
||||||||
T2 |
|
dt |
2 |
dt |
|
dt |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||||
где u(t) |
– входной; |
y(t) |
– выходной сигналы. |
|
|
|
||||||||
Необходимо определить передаточную функцию в операторной |
||||||||||||||
форме. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение. Используя, оператор дифференцирования |
p = d / dt , |
|||||||||||||
данное уравнение можно записать в операторной форме:
T22 p2 y(t) + T1 py(t) + y(t) = K τ1 pu(t) + u(t) .
Если выделить операторы преобразования входного и выходного сигналов, то дифференциальное уравнение «вход-выход» принимает следующий вид:
2 |
p |
2 |
+ T1 p +1) y(t) = K (τ1 p +1)u(t) , |
||
(T2 |
|
|
|||
2 |
p |
2 |
+ T1 p + 1) – собственный оператор; (τ1 p + |
||
где (T2 |
|
|
|||
воздействия.
Тогда получаем искомую передаточную функцию, ние оператора воздействия к собственному оператору, в
|
|
|
τ |
p +1 |
|
|
W ( p) = K |
|
|
|
1 |
|
. |
|
2 |
|
2 |
|
||
|
T |
p |
+ T p +1 |
|
||
|
|
|
|
|||
|
2 |
|
|
1 |
|
|
1) |
– оператор |
|
как отношевиде
8
