
Практическое занятие № 4
КАЧЕСТВО СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
Рис. 1. Структурная схема САУ
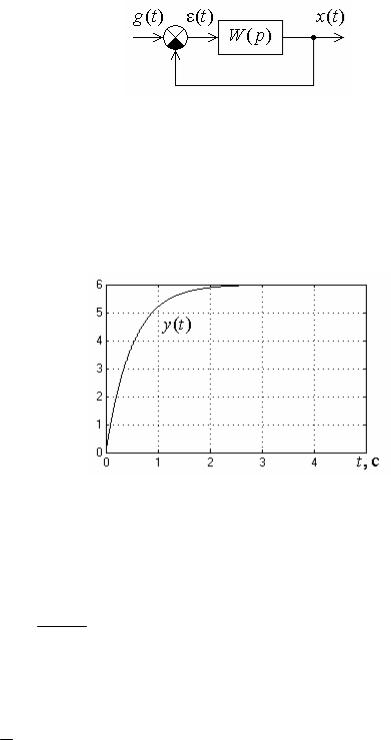
Задача 1. По переходному процессу y(t) (рис. 2) на ступенчатый сигнал вида u(t) 4 1(t) определить передаточную функцию динамического инерционного звена первого порядка.
Рис. 2
Решение. Передаточная функция инерционного звена первого порядка
W(p) k . Tp 1
Установившееся значение выходного сигнала yуст 6. Тогда значение коэффициента передачи
k6 1,5. 4
1
Постоянная времени T звена определяется по касательной, проведенной к переходной функции при t 0. Тогда T 0,5 с.
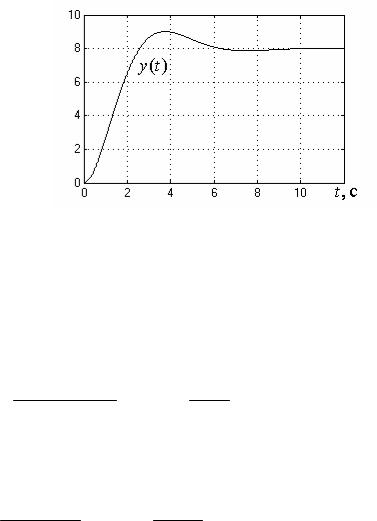
Задача 2. Оценить прямые показатели качества САУ, переходный процесс y(t) на выходе которой при подаче ступенчатого задающего воздействия g0(t) 10 1(t) имеет следующий вид:
Рис. 3
Решение. Установившееся значение выходного сигнала yуст 8.
Максимальное значение – yмакс 9. Тогда величина перерегулирования
макс yмакс yуст 100% 9 8100% 12,5%.
yуст 8
Время регулирования tрег 5,5 с.
Установившаяся ошибка системы
εуст yуст g0 100% 8 10100% 20%. g0 10
Задача 3. Какой должна быть величина коэффициента передачи пропорционального регулятора в системе (рис. 1), замкнутой единичной обратной связью с передаточной функцией разомкнутой части
W(p) |
k |
, |
|
(Tp 1)p |
|||
|
|
чтобы переходный процесс не имел перерегулирования?
Решение. Найдем передаточную функцию замкнутой системы:
2

Ф(p) |
W(p) |
|
k |
. |
|
|
|||
1 W(p) |
|
Tp2 p k |
||
Приведем полученное выражение к стандартной передаточной функции динамического звена второго порядка
1
Ф0(p) T02 p2 2T0ξ0 p 1.
Известно, что для такого звена при ξ0 1 переходные процессы имеют монотонный характер.
Тогда
T |
T |
; ξ |
0 |
|
1 |
|
. |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||||||
0 |
k |
|
2 Tk |
1 |
|
|
|
0,25 |
|
|||||||
Следовательно, при |
|
|
1 |
или при k |
переходные про- |
|||||||||||
|
|
|
|
|
||||||||||||
|
|
|
|
|
2 |
|
Tk |
|
|
|
T |
|||||
цессы не будут иметь перерегулирование.
При k 0,25/T характеристическое уравнение системы принимает следующий вид
Tp2 p k T2 p2 Tp 0,25 (Tp 0,5)2 0.
Этому случаю соответствуют два кратных корня p 0,5/T .
1,2
Задача 4. Передаточная функция разомкнутой САР (рис. 1) имеет вид
W(p) k . Tp 1
Определить установившееся значение ошибки замкнутой системы на входное воздействие g(t) 1 t.
Решение. Определим первую и вторую производные входного воздействия g(t):
g(t) 1; g(t) 0.
Найдем передаточную функцию замкнутой системы относительно ошибки:
Фε(p) |
|
1 |
|
|
Tp 1 |
. |
|
1 W(p) |
|
||||||
|
|
Tp 1 k |
|||||
Коэффициенты ошибки: |
|||||||
C0 Фε(0) |
1 |
; |
|
|
|||
|
|
|
|||||
|
|
1 k |
|
|
|
||
3

Фε(p) |
|
|
Tp 1 |
|
|
Tk |
|
|||
C1 |
|
|
|
|
|
|
|
|
|
. |
p |
|
|
|
(1 k)2 |
||||||
|
p 0 |
|
p Tp 1 k p 0 |
|
|
|||||
Тогда установившееся значение ошибки:
1Tk
εв(t) C0g(t) C1g(t) 1 k (1 t) (1 k)2 .
Задача 5. Передаточная функция разомкнутой САР (рис. 1) имеет вид
W(p) k . p(Tp 1)
Определить установившееся значение ошибки замкнутой системы на входное воздействие g(t) 1 t.
Решение. Найдем передаточную функцию замкнутой системы относительно ошибки:
Фε(p) |
|
|
1 |
|
|
(Tp 1)p |
. |
|
|
|
|
|
||||||
1 W(p) |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
(Tp 1)p k |
|
|
|
|
|
|||||||||
Коэффициенты ошибки: |
|
|
|
|
|
|
|
|||||||||||
C0 Фε(0) 0; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Фε(p) |
|
|
|
(Tp 1)p |
|
1 |
|
|||||||||||
C1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
p |
|
|
p (Tp 1)p |
|
k |
||||||||||||
|
|
p 0 |
|
|
k p 0 |
|
|
|||||||||||
Тогда установившееся значение ошибки:
εв(t) C0g(t) C1g(t) 1. k
Задача 6. Для системы (рис. 4) определить, значение установившейся ошибки системы.
Рис. 4
Передаточная функция системы в разомкнутом состоянии
4

W(p) |
k |
, |
|
(T1p 1)(T2 p 1)p |
|||
|
|
где k 10с 1; T1 0,2с; T2 0,02с.
Входной сигнал меняется по закону g(t) 5 20t 20t2, возмущение f (t) 0.
Решение. Найдем передаточную функцию замкнутой системы относительно ошибки
Фε(p) |
E(p) |
|
|
1 |
|
(T1p 1)(T2 p 1)p |
|
|
1 W(p) |
(T1p 1)(T2 p 1)p k |
|||||
|
G(p) |
|
|
||||
|
TT p3 |
(T T )p |
2 p |
|
|||
|
|
1 2 |
|
1 |
2 |
|
. |
|
|
(T T )p2 |
p k |
||||
TT p3 |
|
||||||
1 |
2 |
|
1 |
2 |
|
|
|
Коэффициент ошибки C0 0, так как система астатическая. Коэффициенты ошибок C0, C1, C2 определяют по (9.12) или разложением в ряд по возрастающим степеням p функции Фε(p) делением числителя на знаменатель:
Фε(p) C1p C2 p2 kp [(T1 T2k)2k 1]p2 .
Коэффициенты C3, вычислять не имеет смысла, так как функция g(t) имеет только две производные, не равные нулю.
Определим первую и вторую производные входного воздействия g(t):
g(t) 20 40t; g(t) 40.
Тогда
εв(t) С1g(t) C2g(t) 2,48 4t.
Задача 7. Дано характеристическое уравнение замкнутой системы автоматического управления
p2 p 1 0.
Определить корневые оценки качества системы. Решение. Корни характеристического уравнения:
p α jβ |
1 |
|
1 |
1 |
1 j 3 |
. |
|
|
|
||||
1,2 |
2 |
4 |
2 |
|
||
|
|
|||||
Тогда
5
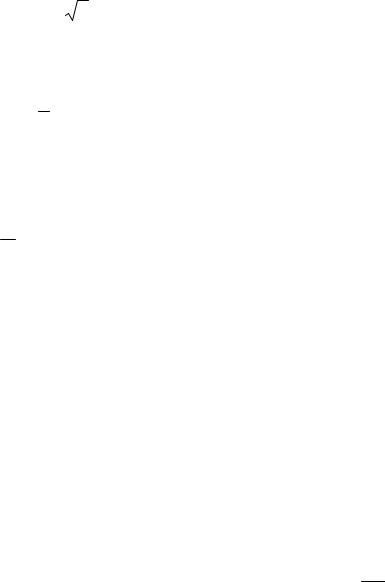
α 1/2; |
β 3/2. |
Следовательно, степень устойчивости
|α| 1/2;
колебательность
|β/α| 
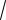 3; tg ; 60
3; tg ; 60
Задача 8. Передаточная функция разомкнутой системы автоматического управления (рис. 1)
W(p) k . p
Определить оптимальное значение коэффициента передачи, соответствующее минимуму интегральной оценки
I [ε2(t) T2ε2(t)]dt.
0
Решение. Передаточная функция замкнутой системы по выходу
Ф(p) |
k |
|
1 |
, гдеτ 1/k; x(t) 1 e kt . |
p k |
|
|||
|
|
τp 1 |
||
Тогда значение ошибки системы
ε(t) g(t) x(t) 1 1 e kt e kt;ε(t) k
Интегральная оценка системы
|
|
I (e 2kt T2k2e 2kt)dt (1 T2k2) e 2kt |
|
0 |
0 |
Условие минимума интегральной оценки
dI |
|
2T2k 2k 2(1 T2k2) |
T |
2k |
2 1 |
0. |
|||
|
|
|
|
|
|
|
|
|
|
dk |
4k |
2 |
|
2k2 |
|||||
|
|
|
|
||||||
e kt.
dt 1 (1 T2k2). 2k
Оптимальное значение коэффициента передачи, соответствующее минимуму I :
T2k2 1 0, тогда kопт T .
Задача 9. Передаточная функция разомкнутой системы (рис. 1) имеет вид
|
A(p) |
|
a pm |
a pm 1 |
a |
m 1 |
p a |
m |
|
|
W(p) |
|
|
0 |
1 |
|
|
. |
|||
B(p) |
b pn |
b pn 1 |
b |
|
|
|
||||
|
|
|
p b |
|
|
|||||
|
|
0 |
1 |
n 1 |
|
n |
||||
6
Каковы условия получения астатизма нулевого, первого, второго порядка?
Решение. Передаточная функция разомкнутой системы
W(p) |
|
A(p) |
, |
|
|
p |
|
|
|||
|
|
νB (p) |
|
||
|
|
|
1 |
|
|
где ν – порядок астатизма. |
|
||||
Тогда |
|
|
|
||
ν 0 |
– статическая система: bn 0; |
|
|||
ν 1 |
– система с астатизмом 1 порядка: bn 0;bn 1 0; |
|
|||
ν 2 |
– система с астатизмом 2 порядка: bn bn 1 0;bn 2 |
0. |
|||
Передаточная функция замкнутой системы (рис. 1) имеет вид Передаточная функция замкнутой системы
W(p) |
W(p) |
|
|
|
|
|
|
A(p) |
|
|
|
|
|
|
|
|
A(p) |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
1 W(p) |
|
|
B(p) A(p) |
pνB (p) A(p) |
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a pm |
a pm 1 |
a |
m 1 |
p a |
m |
|
|
|
|
||||||||||||||||||||
|
|
|
0 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
||||||||||
b pn |
(b |
|
|
|
|
|
)p |
2 (b |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
a |
m 2 |
|
|
|
a |
m 1 |
)p b a |
m |
|
||||||||||||||||||||||
0 |
|
|
n 2 |
|
|
|
|
|
|
|
n 1 |
|
|
|
|
|
n |
|
|||||||||||||||
|
a pm |
|
a pm 1 |
a |
m 2 |
p2 a |
m 1 |
p a |
m |
|
|
|
|
|
|||||||||||||||||||
|
0 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|||||||||||
c pn c pn 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
c |
n 2 |
p2 c |
n 1 |
p c |
n |
|
|
|
|
|
|
|
|
|||||||||||||||||||
0 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
ν 0 |
– статическая система: am cn; |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
ν 1 |
– система с астатизмом 1 порядка: am cn; am 1 |
cn 1; |
|||||||||||||||||||||||||||||||
ν 2 |
– система с астатизмом 2 порядка: am cn; am 1 |
cn 1; |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
am 2 cn 2. |
|
|||||||
Задача 10. В статической системе регулирования (рис. 5) пере- |
|||||||||||||||||||||||||||||||||
даточная функция W(p) |
|
|
k |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
Tp 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Рис. 5
7
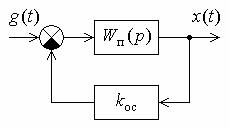
Определить коэффициент передачи обратной связи kос, при котором замкнутая система приобретает свойство астатизма первого порядка.
Решение. Передаточная функция замкнутой системы
Ф(p) |
|
W(p) |
|
|
|
x |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
1 W(p)kос g |
|
|
|
|
|
|
|||||||
Ошибка системы |
|
|
1 W(p)kос W(p) |
|||||||||||
|
|
|
|
|
|
W(p) |
|
|
||||||
ε g |
x (1 |
|
|
|
|
|
)g |
|
|
|
g Фε(p)g. |
|||
1 W(p)kос |
|
|
||||||||||||
|
|
|
|
|
|
|
1 W(p)kос |
|||||||
Передаточная функция замкнутой системы по ошибке |
||||||||||||||
Фε(p) |
1 W(p)kос W(p) |
|
Tp 1 kkос k |
. |
||||||||||
|
|
|||||||||||||
|
|
|
1 W(p)kос |
|
|
|
Tp 1 kkос |
|||||||
Коэффициент позиционной ошибки
C0 Фε(0) 1 kkос k 0. 1 kkос
Тогда
kос 1 1.
k
Задача 11. В статической системе регулирования передаточная
функция разомкнутой САР (рис. 6) W(p) K .
Tp 1
Рис. 6
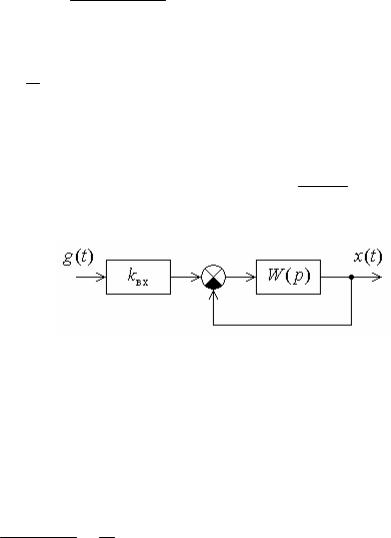
Определить коэффициент передачи входного усилителя kвх, при котором замкнутая система приобретает свойство астатизма первого порядка.
Решение. Передаточная функция замкнутой системы
Ф(p) kвхW(p) x . 1 W(p) g
8
Ошибка системы
ε g x (1 |
kвхW(p) |
)g |
1 W(p) kвхW(p) |
g Фε(p)g. |
||||
|
|
|
|
|||||
|
1 W(p) |
|
|
|
1 W(p) |
|||
Передаточная функция замкнутой системы по ошибке |
||||||||
Фε(p) |
1 W(p) kвхW(p) |
|
Tp 1 k kвхk |
. |
||||
|
|
|||||||
|
1 W(p) |
|
|
|
Tp 1 k |
|||
Коэффициент позиционной ошибки
C0 Фε(0) 1 k kвхk 0. 1 k
Тогда
kвх 1 1
k
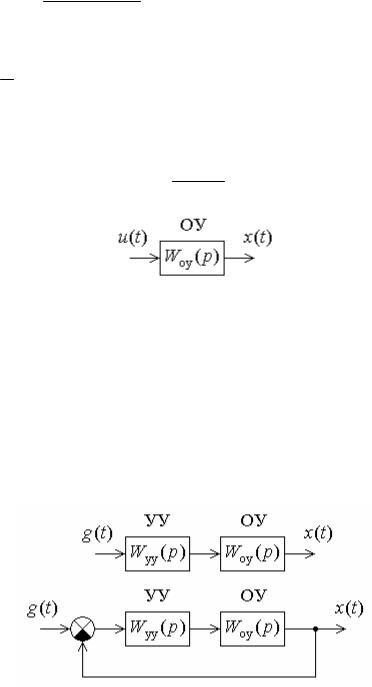
Задача № 12. Имеется линейный объект управления (рис. 7) с
передаточной функцией W(p) 5 . 2p 1
Рис. 7
Используя замкнутый и разомкнутый принципы управления, предложить структурные схемы системы управления данным объектом, обеспечивающие значение выходной координаты объекта равное
100.
Решение. Структурная схема разомкнутого управления и структурная схема замкнутого управления приведены на рис. 8
Рис. 8
9
где для разомкнутого управления g(t) 1, W1(p) 20(2p 1) , τ 0; τp 1
для замкнутого управления g(t) 100, W1(p) k 2p 1, k . p
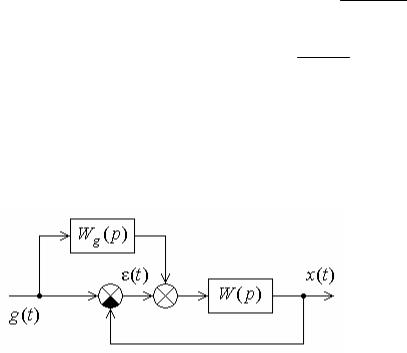
Задача 13. Определить требуемый уровень компенсирующего сигнала по первой производной от входного воздействии, при котором устраняется скоростная ошибка системы (рис. 9),
Рис. 9
где
W(p) |
k |
; Wg (p) kg p. |
|
p(Tp 1) |
|||
|
|
Решение. Уравнение ошибки относительно входного воздейст-
вия
|
|
|
|
|
|
|
|
|
W(p) |
|
|
|
Wg (p)W(p) |
|
1 Wg (p)W(p) |
|
|||||
(t) g(t) |
|
|
|
|
|
g(t) |
|
|
g(t) |
|
g(t). |
||||||||||
1 W(p) |
|
1 W(p) |
1 W(p) |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Передаточная функция замкнутой системы по ошибке |
|
||||||||||||||||||||
Фε(p) |
1 Wg (p)W(p) |
Tp2 p kgkp |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
||||
|
|
|
|
1 W(p) |
|
|
|
|
Tp2 p k |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Коэффициент скоростной ошибки |
|
|
|
|
|||||||||||||||||
C |
|
Ф |
ε |
(p) |
|
1 kgk |
|
|
|
|
|||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
p |
|
|
|
|
|
k |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
p 0 |
|
|
|
|
|
|
|
|
|
|||||||
Условие устранения скоростной ошибки 1 kgk 0.
Следовательно kg 1/k.
10
