
Практическое занятие № 3
УСТОЙЧИВОСТЬ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
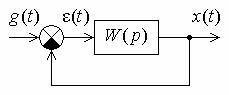
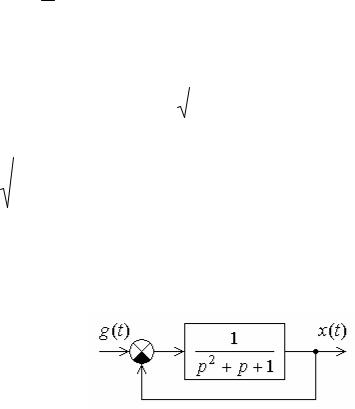
Рис. 1. Структурная схема САУ
Задача 1. Характеристическое уравнение замкнутой системы имеет вид
p3 p2 2p 1 0.
Определить устойчивость системы. Решение.
a1 a3 |
0 |
|
1 |
1 |
0 |
||
|
a2 |
0 |
|
|
|
2 |
|
a0 |
|
1 |
0 . |
||||
0 |
a |
a |
|
0 |
1 |
1 |
|
|
1 |
3 |
|
|
|
|
|
Условия устойчивости
a0 0, a1 0, a2 0, a3 0, a1a2 a0a3 0
Все коэффициенты положительные, тогда
2 a1a2 a0a3 1 2 1 1 1 0.
Следовательно, система устойчивая.
Задача 2. Характеристическое уравнение замкнутой системы имеет вид
5p3 2p2 3p 1 0.
Определить устойчивость системы.
Решение. Система неустойчивая, так как a2 3 0.
Задача 3. Характеристическое уравнение замкнутой системы имеет вид
1

p4 p3 p2 p 1 0.
Определить устойчивость системы. Решение.
a1 a3 |
0 |
0 |
1 1 0 |
0 |
||||
|
|
a4 |
|
|
|
|
|
|
a0 a2 |
0 |
1 1 1 |
0 |
|||||
0 |
a1 a3 |
0 |
0 1 1 |
0 |
||||
0 |
a a |
2 |
a |
4 |
|
0 1 1 |
1 |
|
|
0 |
|
|
|
|
|
||
Условия устойчивости
a0 0, a1 0, a2 0, a3 0, a4 0,
a1a2a3 a0a32 a12a4 0.
Все коэффициенты положительные, тогда
3 a1a2a3 a0a32 a12a4 1 1 1 1 1 1 1 1 1 1 0.
Следовательно, система неустойчивая.
Задача 4. Передаточная функция разомкнутой системы с единичной обратной связью
W((p) k . p(Tp 1)
Определить условия устойчивости замкнутой системы. Решение.
Ф(p) |
W(p) |
|
k |
. |
|
|
|||
1 W(p) |
|
Tp2 p k |
||
Для устойчивости необходимо, чтобы a0 0;a1 0; a2 0, т.е.
T 0;1 0; k 0.
Условия устойчивости T 0; k 0
Задача 5. Определить устойчивость замкнутой системы, если передаточная функция разомкнутой системы с единичной обратной связью имеет вид
k
W((p) p2(Tp 1).
Решение.
2
Ф(p) |
W(p) |
|
k |
|
. |
|
Tp3 p2 |
|
|||
1 W(p) |
|
k |
|||
Характеристическое уравнение замкнутой системы
Tp3 p2 k 0, |
a2 0. |
Замкнутая система структурно неустойчива, т.е. неустойчива при любых значениях k и T .
Задача 6. Передаточная функция разомкнутой САУ имеет вид
W(p) |
K(T3p 1) |
. |
|
p(T1p 1)(T2 p 1)
Определить значение постоянной времени T3, при котором замкнутая система находится на границе устойчивости.
Решение.
Ф(p) |
k(T3 1) |
. |
|
p(T1p 1)(T2 p 1) k(T3p 1)
T1T1p3 (T1 T2)p2 (1 kT3)p k 0.
Условия устойчивости
a0 0, a1 0, a2 0, a3 0, a1a2 a0a3 0.
Отсюда
(T1 T2)(1 kT3) kT1T2 |
0; или |
|
|
|
||||||||||
1 kT |
|
kT1T2 |
|
; или T |
|
T1T2 |
|
|
1 |
. |
||||
|
|
|
|
|
||||||||||
|
3 |
T T |
3 |
T T |
|
k |
||||||||
Тогда |
1 |
2 |
|
|
|
1 |
2 |
|
|
|
||||
T1T2 |
|
|
|
1 |
|
|
|
|
|
|
|
|||
T |
|
|
|
. |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
||||||
3кр |
|
T T |
|
k |
|
|
|
|
|
|
||||
|
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
Задача 7. Определить с помощью критерия Михайлова условия устойчивости системы автоматического регулирования с передаточной функцией в разомкнутом состоянии
W p |
k |
|
k |
. |
p(T1p 1)(T2 p 1) |
|
|||
|
|
Q(p) |
||
Решение. Характеристическое уравнение замкнутой системы
D(p) Q(p) k p(T1p 1)(T2 p 1) k 0.
3
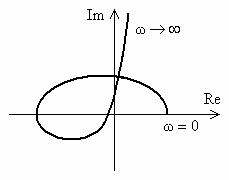
Построим годограф Михайлова
D j j 1 j T1 1 j T2 U jV ,
где
U(ω) k ω2 T |
T |
; |
(3.1) |
1 |
2 |
|
|
V(ω) ω ω3T1T2. |
|
|
|
Cистема будет на границе устойчивости, если годограф D( jω) пройдет через начало координат. Величина kкр может быть опреде-
лена из уравнений:
V(ω0) 0;U(ω0) 0, |
(3.2) |
где ω0 – частота, соответствующая точке пересечения годографа D( jω) с началом координат.
Решая уравнения (3.1) и (3.2), получим
ω20 1/T1T2;
kкр ω02(T1 T2).
Следовательно
k kкр (T1 T2)/T1T2 1/T1 1/T2.
Задача 8. САУ имеет характеристическое уравнение пятого порядка. Годограф Михайлова имеет вид
Рис. 2
Определить число корней характеристического уравнения в правой и левой части комплексной плоскости.
Решение.
4
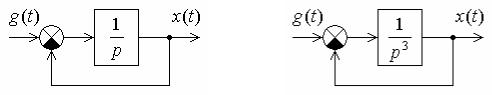
l m 5; |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|||
argD(jω) (l m) |
|
|
|
. |
||
2 |
2 |
|||||
|
0 ω |
|
|
|||
Отсюда получаем:
l m 5;
l m 1.
Тогда число левых корней l 3, число правых корней m 2.
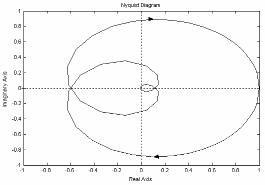
Задача 9. С помощью критерия Найквиста определить устойчивость систем, приведенных на рис. 3 и рис. 4.
Рис. 3 Рис. 4
Решение. САУ на рис. 3 – устойчивая, на рис. 4 – структурно неустойчивая.
Задача 10. Применить критерий Найквиста для определения предельного (критического) коэффициента системы регулирования с передаточной функцией разомкнутой системы
W p |
k |
. |
|
p(T1p 1)(T2 p 1) |
|||
|
|
||
Решение. Величина kкр определяется из условия |
|||
|W(jω-π)| 1, |
(3.3) |
||
где ω-π – частота, на которой годограф пересекает отрицательную действительную полуось. Она может быть получена из уравнения
ImW(jω-π) 0. |
(3.4) |
В рассматриваемом примере числитель передаточной функции W(p) представляет собой действительное число k , поэтому последнее уравнение (3.4) удовлетворяется при значениях ω, обращающих в нуль мнимую часть знаменателя W( jω):
5
Im[ jω-π(1 jω-πT1)(1 jω-πT2)] 0
или
1 T1T2ω-2π 0,
откуда
ω2-π 1/T1T2.
На этой частоте знаменатель представляет собой действитель-
ную величину, равную ω-2π(T1 T2), поэтому
|W(jω-π)| kT1T2 /(T1 T2),
что при подстановке в (3.3) дает kкр (T1 T2)/T1T2 1/T1 1/T2.
Задача 11. Передаточная функция разомкнутой системы равна
W(p) |
K |
, |
|
(Tp 1)n |
|||
|
|
где K 0; T 0; n 0.
Определить условие устойчивости замкнутой системы.
Рис. 5
Решение. Запас устойчивости по амплитуде
1 | A(ω π)| 0.
ФЧХ САУ
(ω) n arctg(ωT).
Для точкиω ω π
(ω-π) n arctg(ω-πT) π.
Тогда
6
ω πT tg π. n
Для устойчивости САУ необходимо и достаточно, чтобы
|W(jω)|ω ω π A(ω π) |
|
K |
|
ω ω π 1. |
||||||||
|
|
|||||||||||
|
|
n |
|
|||||||||
1 ( T)2 |
||||||||||||
|
||||||||||||
Тогда условие устойчивости не зависит от T : |
||||||||||||
|
|
|
|
|
n |
|
|
|
|
|||
|
|
2 |
|
|
|
|
|
|||||
K |
|
1 tg |
|
|
|
|
|
|
|
|||
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
n |
|
|
|
|
||||
Задача 12. С помощью критерия Найквиста определить устойчивость системы, приведенной на рис. 6.
Рис. 6
Решение. АФЧХ разомкнутой системы
1 |
|
|
|
|
(1 2) j |
|
|
|
|
|
|||||||||||
W(jω) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U(ω) jV(ω), |
||||
2 j 1 |
|
(1 2) |
2 2 |
||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||
где U(ω) |
|
1 ω2 |
|
; V(ω) |
|
|
|
|
ω |
|
. |
||||||||||
(1 ω2)2 |
ω2 |
|
(1 ω2)2 |
ω2 |
|||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
ω |
|
U |
|
V |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
0 |
|
1 |
|
0 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
0 |
|
0 |
|
|
|
|
|
|||
ФЧХ разомкнутой системы |
|
|
|
|
|
ω-π |
|
|
|||||||||||||
(ω) arctg |
ω |
|
; (ω-π) arctg |
. |
|||||||||||||||||
|
|
|
|
||||||||||||||||||
|
|
1 ω2 |
|
|
|
|
|
|
|
|
|
|
|
1 ω-2π |
|
|
|||||
Тогда, если
7
tg( ) 1ωω-π-2π 0, то -π и U( -π) 0.
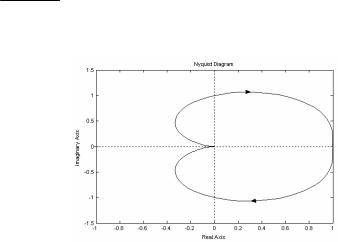
Рис. 7
Таким образом, годограф W( jω)находится в 4 и 3 квадрантах, не охватывает точку ( 1, j0) и, следовательно, САУ – устойчивая.
Задача 13. Определить область устойчивости для коэффициентов α и β характеристического уравнения
p3 αp2 βp 1 0.
Решение. В этом случае
P(p) p2;Q(p) p; R(p) p3 1.
Уравнение для границы D-разбиения:
αω2 jβω jω3 1 0.
Уравнения для действительной и мнимой частей:
αω2 1 0, βω ω3 0.
Отсюда α 1/ω2, β ω2.
Исключая параметр ω, получаемграницуD-разбиения:
αβ 1.
Так как α 0,β 0, то
|
2 |
0 |
3 0. |
|
0 |
|
|
Если значение α откладывается по горизонтальной оси, а значение β – по вертикальной оси, то областью устойчивости является область в первом квадранте выше гиперболы αβ 1.
8
