Практическое занятие № 2
ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ЗВЕНЬЕВ И СИСТЕМ
RC
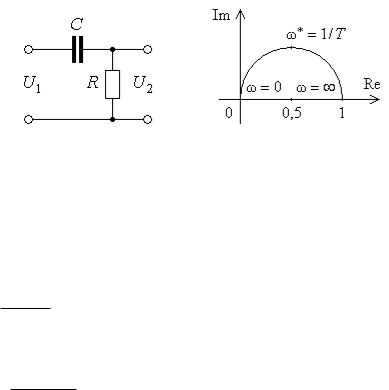
Задача 1. Построить амплитудно-фазовую характеристику цепи , представленной на рис. 1, а, где R = 1 кОм, C =10 мкФ.
а |
б |
Рис. 1
Решение. Передаточная функция цепи, согласно, задачи 1.1, равна
W ( p) = |
Tp |
. |
|
|
|
||
Tp +1 |
|
|
|
||||
|
|
|
|
|
|||
Тогда АФЧХ имеет вид |
|
||||||
W ( jω) = |
jωT |
, |
|
|
|||
|
|
|
|
|
|||
|
jωT |
+1 |
|
|
|||
где T = RC =10 |
3 |
10 |
−5 |
=10 |
−2 |
||
|
|
|
|||||
с.
Преобразуем полученное выражение АФЧХ таким образом, чтобы оно представляло собой комплексное число в алгебраической форме:
W ( jω) = U (ω) + jV (ω) = |
|
ω2T 2 |
|
|
+ j |
|
ωT |
|
; |
|||||
|
2 |
2 |
|
2 |
2 |
|||||||||
|
|
|
|
|
|
|
|
|
||||||
|
|
|
1 + ω T |
|
|
|
|
1 + ω T |
|
|
||||
U (ω) = |
ω2T 2 |
|
; V (ω) = |
|
ωT |
|
|
. |
|
|
|
|
||
|
2 |
2 |
|
2 |
|
|
|
|
||||||
2 |
|
|
|
|
|
|
|
|
||||||
1 + ω T |
|
|
|
1 + ω T |
|
|
|
|
|
|
||||
Задаваясь отдельными значениями частоты ω , можно по форму- |
||||||||||||||
лам вычислить ряд |
значений |
|
U (ω) |
и |
V (ω) , |
и построить по ним |
||||||||
1
АФЧХ цепи. Например, для предельных значений частоты можно получить следующую таблицу.
|
ω |
U (ω) |
|
|
V (ω) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
|
|
0 |
|
|
|
1/ T |
0,5 |
|
|
0,5 |
|
|
|
|
1 |
|
|
0 |
|
|
Однако анализ выражений |
U (ω) |
и |
V (ω) |
показывает, что для |
|||
АФЧХ может быть получено аналитическое выражение.
Пусть
ωT
=
a
, тогда
U (ω) = a |
2 |
/(1 + a |
2 |
) |
|
|
и
V (ω) =
a /(1 +
a |
2 |
) |
|
. Сле-
довательно,
U (ω) / V (ω) =
a
,
отсюда
U (ω) = U |
2 |
(ω)/[U |
2 |
(ω) +V |
2 |
(ω)] |
|
|
|
или U |
2 |
(ω) +V |
2 |
(ω) = U (ω) . Тогда |
|
|
||||
|
|
|
|
|||||||
V (ω) +[U (ω) − 0,5] |
2 |
= 0,5 |
2 |
. |
|
|
||||
|
|
|
|
|||||||
Для положительных частот АФЧХ является полуокружностью, |
||||||||||
расположенной в верхней полуплоскости с центром в точке ( 0,5; |
j0 ) |
|||||||||
и радиусом 0,5 (рис. 1, б). |
|
|
|
|
||||||
Из полученных выражений видно, что при ω = 0 |
W ( jω) = 0 + j0 , |
|||||||||
а при ω =
W ( jω) = 1 +
j0
. Частоты, соответствующие промежуточ-
ным точкам кривой, могут быть найдены следующим образом. Аргумент комплексного числа
(ω) = arg W ( jω) = |
V (ω) |
= arg tg |
|
U (ω) |
|||
|
|
поэтому луч, проведенный из начала
1 |
= arg tg |
100 |
, |
|
T |
|
|||
|
|
координат под углом (ω) к оси
абсцисс, пересекает АФЧХ в точке, в которой величина ω определя-
ется через (ω) последним выражением. Например, для |
(ω) = 45 |
частота ω =1/ T =100 1/с. |
|
Задача 2. Передаточная функция динамического звена
W ( p) = K . p(Tp +1)
Вывести аналитические выражения частотных характеристик и построить амплитудно-фазовую частотную характеристику звена при
K =10 с-1; T = 0,25 с .
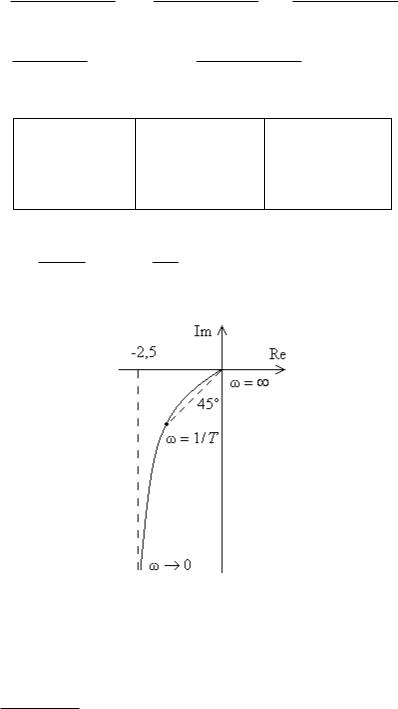
Решение. АФЧХ звена
2
W ( jω) = |
k |
= − |
kTω |
|
|
− |
|
jω( jωT +1) |
|
2 |
|
2 |
|||
|
|
ω(1 + T |
ω |
) |
|||
|
|
|
|
||||
j |
k |
|
|
|
|
|
2 |
|
2 |
|
|
|
ω(1 + T |
ω |
) |
||
|
|
|
;
U (ω) = − |
kT |
|
|
; |
|
|
2 |
|
2 |
||
|
1 + T |
ω |
|
||
|
|
|
|
||
V (ω) = − |
k |
|
|
ω(1 |
+ T |
2 |
ω |
2 |
) |
|
|
.
ω |
U (ω) |
V (ω) |
|
|
0 |
-2,5 |
|
1 / T |
0,5 |
0,5 |
|
||
|
0 |
0 |
( ) = arctg U (ω) = arctg T1ω . При
ω = T |
−1 |
|
(ω) = 45 .
Рис. 2
Задача 3. Передаточная функция динамического звена
W ( p) = |
k |
. |
|
p(Tp +1) |
|||
|
|
Вывести аналитические выражения и построить логарифмические амплитудные и фазовые частотные характеристики звена при
k = 10 с−1 , T = 10−1 c ; k = 100 с−1 |
, |
T = 10−1 c ; |
k = 10 с−1 , T = 10−2 c . |
|||||
Решение. АФЧХ звена |
|
|
|
|
|
|||
W ( jω) = |
k |
|
kTω |
− j |
k |
; |
||
|
= − |
|
|
|||||
jω( jωT +1) |
ω(1 + T 2ω2 ) |
ω(1 + T 2ω2 ) |
||||||
3
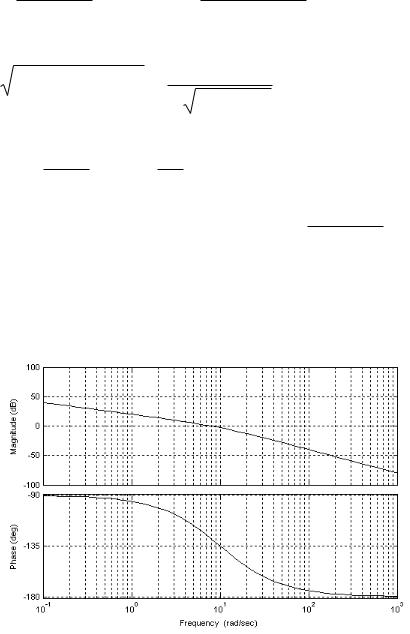
U (ω) = − |
kT |
|
|
; |
|
|
2 |
|
2 |
||
|
1 + T |
ω |
|
||
|
|
|
|
||
АЧХ звена
V (ω) = − |
k |
|
|
ω(1 |
+ T |
2 |
ω |
2 |
) |
|
|
.
A(ω) = U |
2 |
(ω) +V |
2 |
(ω) = |
k |
|
|
|
||
|
|
|
|
|||||||
|
|
|
2 |
|
2 |
|||||
|
|
|
|
|
|
ω |
1 + T |
ω |
||
|
|
|
|
|
|
|
|
|||
ФЧХ звена |
|
|
|
|
|
|
|
|
|
|
(ω) = arctg |
V (ω) |
= arctg |
1 |
. |
|
|
|
|||
U (ω) |
Tω |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
||
.
Тогда ЛАХ звена
L(ω) = 20 lg A(ω) = 20 lg k − 20 lg ω − 20lg 
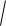1 + T 2ω2 .
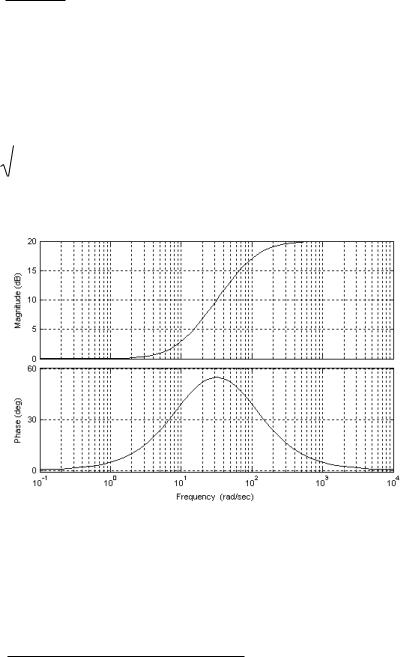
Логарифмические частотные характеристики для первого варианта числовых значений, построенные в пакете Control системы Matlab представлены на рис. 3.
Рис. 3
Для второго варианта числовых значений ЛАЧХ смещается вверх до 20 lg 100 = 40 дб при lg ω = 0 ; ЛФЧХ остается неизменной.
Для третьего варианта числовых значений ЛАЧХ остается неизменной; ЛФЧХ имеет излом при lg ω = 1/10−2 = 2 .
4
Задача 4. Передаточная функция динамического звена
|
T p +1 |
|
||
W ( p) = |
1 |
|
. |
|
T |
p +1 |
|||
|
|
|||
|
2 |
|
|
|
Вывести аналитические выражения частотных характеристик и построить логарифмические амплитудные и фазовые частотные ха-
рактеристики звена при T1 |
= 10 |
−1 |
c; T2 |
= |
||||||
|
||||||||||
W ( jω) = (T1 jω +1) /(T2 jω +1) ; |
|
|
||||||||
|
|
|
|
|
|
|||||
A(ω) = |
[(T ω)2 +1] /[(T ω)2 |
+1] ; |
( |
|||||||
|
1 |
|
|
2 |
|
|
|
|
|
|
L(ω) = |
10 lg[(T ω) |
2 |
+1] |
−10 lg[(T ω) |
2 |
|||||
|
|
|||||||||
|
1 |
|
|
|
|
2 |
|
|
||
10 |
−2 |
|
|
ω) = |
|
+1] . |
|
c.
arctg
T1ω
− arctg
T2ω
;
Рис. 4
Задача 5. САР в разомкнутом состоянии имеет передаточную функцию
|
K (T |
p + 1) |
|
W ( p) = |
4 |
|
. |
|
|
||
p(T p + 1)(T |
p + 1)(T p + 1) |
|
|
1 |
2 |
3 |
|
Построить логарифмическую АЧХ и определить диапазон изме-
нения ФЧХ при K = 100 с-1 |
; T |
= 10−1 |
c; T |
= T |
= 10 |
−3 c; T = 10−2 |
c. |
|
1 |
|
2 |
3 |
|
4 |
|
5
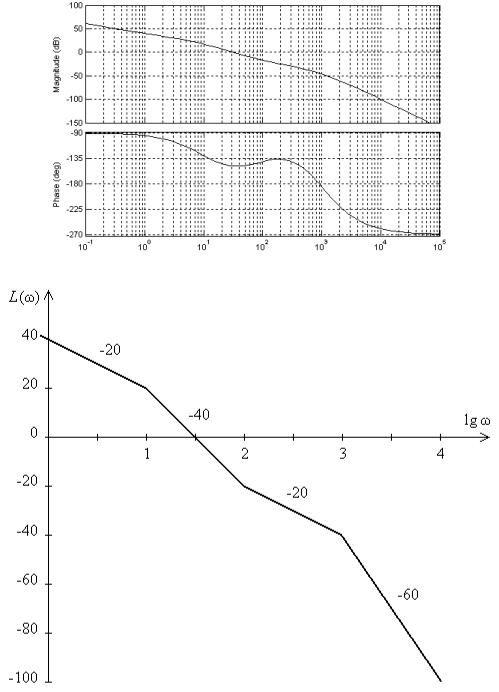
Рис. 5
ЛАЧХ имеет вид ломанной прямой с участками, имеющими отрицательные наклоны: – 20, – 40, – 20, – 60 дБ/дек.
ЛФЧХ изменяется от − π/2 до − 3π/2.
6
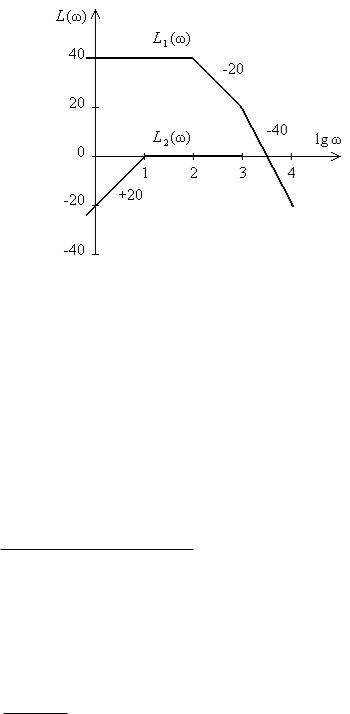
Задача 6. На рис. 6 изображены асимптотические логарифмические амплитудные характеристики минимально-фазовых звеньев. Найти передаточные функции этих звеньев.
Рис. 6
Решение. По виду низкочастотных асимптот первое звено является статическим звеном, второе – дифференцирующим.
Для первого звена.
L1(ω) |ω=1= 20 lg k1 = 40 . Тогда |
1 |
. Точки излома ЛАХ: |
|
k = 100 |
|
lg ω1 = 2; lg ω2 = 3. Тогда T1 = 1/ ω1 = 1/100 = 0,01 с ; T2 = 1/ ω2 = 1/1000 = 0,001 с .
Следовательно, передаточная функция первого звена:
W |
( p) = |
1 |
|
(0,01 p
100 +1)(0,001 p
+1)
.
lg ω3
Для первого звена. |
. Тогда |
|
2 |
|
. Точка излома ЛАХ: |
L1(ω) |ω=1= 20 lg k2 = −20 |
k |
= 0,1 с |
|||
|
|
|
|
||
=1. Тогда T3 =1/ ω3 =1/10 = 0,1 с . |
|
|
|
||
Следовательно, передаточная функция второго звена:
W2 |
( p) = |
0,1p |
. |
||
0,1p |
+1 |
||||
|
|
|
|||
7
Задача 7. Замкнутая система с единичной обратной связью с передаточной функцией Ф( p) имеет АФЧХ, приведенную на рис. 7, а. Определить передаточную функцию разомкнутой системы W ( p) .
а |
б |
Рис. 7. Структурная схема и АФЧХ САУ
АФЧХ, представленная на рис. 7, является АФЧХ инерционного звена первого порядка со следующими параметрами
где
Ф( p) |
|
K = 1 |
; |
|
|
= T
K |
, |
|
Tp +1 |
|
|
|
|
|
|
=10 |
|
=1/ |
|
|
с
.
Передаточная функция замкнутой системы (рис. 7) связана с передаточной функцией разомкнутой системы, как
Ф( p)
=
W ( p) 1 +W ( p)
.
Тогда передаточная функция разомкнутой системы
|
|
|
|
K |
|
|
|
W ( p) = |
Ф( p) |
= |
Tp +1 |
= |
K |
|
|
− Ф( p) |
|
K |
Tp +1 |
− K |
|||
1 |
1 |
− |
|
||||
|
|
Tp +1 |
|
|
|
||
|
|
|
|
|
|
|
|
= |
1 |
|
10 p |
||
|
=
0,1 p
.
Следовательно, разомкнутая система представляет собой интегрирующее звено с передаточной функцией
W ( p) =
K р p
, где
Kр
=
0,1 с
.
8
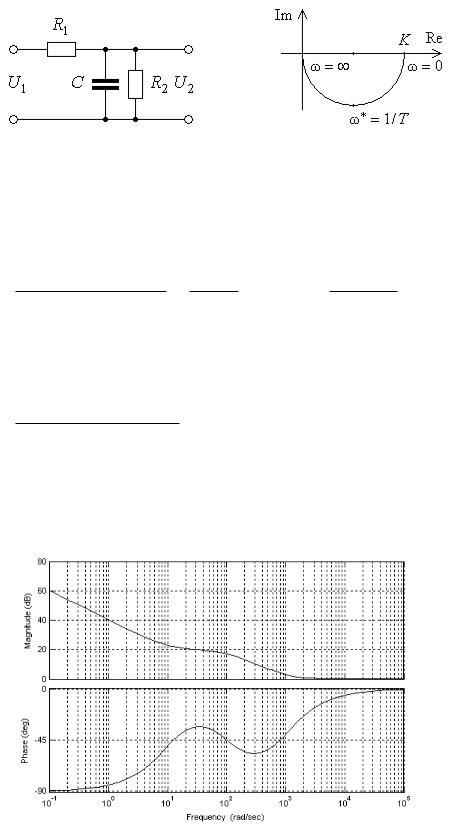
Задача 8. Построить амплитудно-фазовую частотную характеристику цепи, представленной на рисунке.
C
Рис. 8
где
C =1 мкФ; Решение.
W ( p) = R1
R |
= |
1 |
|
+ R2
R2 = 1 МОм. |
||||
R |
|
|
K |
|
2 |
|
= |
|
|
+ R R Cp |
Tp + |
|||
|
||||
1 |
2 |
|
|
|
1
, где
|
R |
|
K = |
2 |
|
|
|
|
R |
+ R |
2 |
1 |
|
;
T
=
KR1C
.
Задача 9. САР в разомкнутом состоянии имеет передаточную функцию
|
K (T p +1)(T |
p +1) |
|
||
W ( p) = |
1 |
2 |
|
. |
|
p(T |
p +1) |
||||
|
|
||||
|
3 |
|
|
|
|
Построить логарифмическую АЧХ и определить диапазон изме-
нения ФЧХ при K =100 |
c |
; |
1 |
|
c; |
2 |
|
c; T3 = 0,01 |
с. |
|
-1 |
|
T |
= 0,1 |
|
T |
= 0,001 |
|
|
Решение.
Рис. 9
9