
- •1. Алгебраическая форма записи комплексного числа
- •2. Плоскость комплексных чисел
- •3. Комплексно сопряжённые числа
- •4.1 Сложение комплексных чисел
- •4.2 Вычитание комплексных чисел
- •4.3 Умножение комплексных чисел
- •4.4 Деление комплексных чисел
- •5. Тригонометрическая форма записи комплексного числа
- •6.1 Умножение комплексных чисел в тригонометрической форме
- •6.2 Деление комплексных чисел в тригонометрической форме
- •6.3 Возведение комплексного числа в целую положительную степень
- •6.4 Извлечение корня целой положительной степени из комплексного числа
- •6.5 Возведение комплексного числа в рациональную степень
- •7. Комплексные ряды
- •7.1 Комплексные числовые ряды
- •7.2 Степенные ряды в комплексной плоскости
- •7.3 Двусторонние степенные ряды в комплексной плоскости
- •8. Функции комплексного переменного
- •8.1 Основные элементарные функции
- •8.2 Формулы Эйлера
- •8.3 Показательная форма представления комплексного числа
- •8.4 Связь между тригонометрическими и гиперболическими функциями
- •8.5 Логарифмическая функция
- •8.6 Общая показательная и общая степенная функции
- •9. Дифференцирование функций комплексного переменного
- •9.1 Условия Коши-Римана
- •9.2 Формулы для вычисления производной
- •9.3 Свойства операции дифференцирования
- •9.4 Свойства действительной и мнимой частей аналитической функции
- •10.1 Способ №1. С помощью криволинейного интеграла
- •10.2 Способ №2. Непосредственное применение условий Коши-Римана
- •10.3 Способ №3. Через производную искомой функции
- •14.1 Нули функции комплексного переменного
- •14.2 Изолированные особые точки функции комплексного переменного
- •14.3 Бесконечно удалённая точка как особая точка функции комплексного переменного
- •15.1 Вычет в конечной точке
- •15.2 Вычет функции в бесконечно удаленной точке

15
8.Функции комплексного переменного
8.1Основные элементарные функции
По определению для всех значений z
|
|
|
|
|
|
|
|
|
|
z |
2 |
|
|
|
|
z |
n |
|
∞ |
|
z |
n |
|
|
|
|
|
|
|
|
|
|
||
еz =1+ z+ |
|
+...+ |
|
+... = ∑ |
|
|
, |
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
n! |
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2! |
|
|
|
|
|
n! |
|
n=0 |
|
|
|
|
|
|
|
|
|
|
|||||
|
z |
2 |
|
|
|
z |
4 |
−...+ (−1) |
n |
z |
2n |
|
∞ |
|
(−1) |
n |
z |
2n |
|
|||||||||||||||
cos z =1− |
|
|
+ |
|
|
|
+... = ∑ |
|
|
|
, |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
(2n)! |
|
||||||||||||||||||||||
2! |
|
4! |
|
|
|
|
|
|
(2n)! |
n=0 |
|
|
|
|
||||||||||||||||||||
|
|
z |
3 |
|
|
|
|
|
(−1) |
n |
z |
2n+1 |
|
∞ |
(−1) |
n |
z |
2n+1 |
|
|
||||||||||||||
sin z = z − |
|
|
+...+ |
|
|
|
|
|
+ |
... = ∑ |
|
|
|
|
|
. |
|
|||||||||||||||||
|
|
|
|
(2n +1)! |
|
|
(2n +1)! |
|
||||||||||||||||||||||||||
|
|
|
3! |
|
|
|
|
|
|
|
|
n=0 |
|
|
|
|||||||||||||||||||
Ряды, стоящие справа, абсолютно сходятся на всей комплексной плоскости и поэтому введение указанных функций корректно.
Тогда по определению tg z = sin z |
, при cos z ≠ 0 и |
ctg z = cos z |
при условии |
sin z ≠ 0. |
||||||||
|
cos z |
|
|
|
|
|
|
sin z |
|
|
|
|
Кроме того, по определению для всех значений z |
|
|
|
|
|
|||||||
|
ch z = |
ez +e−z |
, |
sh z = |
ez −e−z |
|
|
|
||||
|
2 |
2 |
|
, |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||
th z = |
sh z |
= |
|
ez −e−z |
, |
cth z = |
ch z |
= |
ez +e−z |
. |
|
|
ch z |
|
ez +e−z |
sh z |
ez −e−z |
|
|||||||
|
|
|
|
|
|
|
|
|||||
Для комплексных чисел сохраняют свою силу известные формулы для действительных чисел, например:
sin2 z +cos2 z =1,
cos(z1 ± z2 ) = cos z1 cos z2 sin z1 sin z2 , sin(z1 ± z2 ) = sin z1 cos z2 ±cos z1 sin z2 .
Замечание. Определение таких понятий как непрерывность функции в точке, предел функции в точке остаются формально аналогичными действительному случаю.
8.2 Формулы Эйлера
Справедливы формулы
eiz = cos z +i sin z , e−iz = cos z −i sin z .
Тогда
Оглавление Е.Е. Красновский, В.Д. Морозова «Теория функций комплексного переменного»

16
cos z = |
eiz +e−iz |
, |
|
2 |
|||
|
|
||
sin z = |
eiz −e−iz |
. |
|
2i |
|||
|
|
Первую из этих формул чаще всего называют формулой Эйлера. Это название может быть применено и к любой из трёх остальных.
8.3 Показательная форма представления комплексного числа
|
|
Если r , |
ϕ модуль и аргумент комплексного числа, то из тригонометрической формы записи |
||||||||||||||||||||||||||||||
комплексного |
числа |
z = r (cosϕ +i sinϕ) и |
формулы Эйлера получим показательную форму |
||||||||||||||||||||||||||||||
представления комплексного числа z = reiϕ . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
В |
показательной |
форме |
формулы |
Муавра |
приобретают |
простой |
|
вид |
zn = rneinϕ |
и |
|||||||||||||||||||||
n |
|
= n |
rei(arg z+2kπ ) n , где k = 0,1,..., n −1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
(1+ |
|
|
i)5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
Пример. |
Найдём |
|
и |
4 1+ |
|
i . |
Сначала |
представим в |
показательной |
форме |
|||||||||||||||||||||
|
|
3 |
3 |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
π |
π i |
|
|
|
|
5 |
|
5 |
|
5π |
i |
|
|
5π |
i |
|
|
комплексное |
число |
1 |
|
|
|
|
|
|
. Тогда |
(1+ |
3i) |
= 2 |
|
|
и |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
+ 3i = 2 cos |
+i sin |
|
= 2e3 |
|
|
e 3 |
= 32e 3 |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 1+
1+
 3i = 4
3i = 4 2ei(π
2ei(π 3+2kπ )
3+2kπ ) 4 , где k = 0,1,2,3 .
4 , где k = 0,1,2,3 .
8.4 Связь между тригонометрическими и гиперболическими функциями
Справедливы следующие соотношения |
|
|
||
|
|
sin iz = i sh z , |
sh iz = i sin z |
|
|
|
cosiz =ch z , |
ch iz = cos z |
|
|
|
tg iz = i th z , |
th iz = i tg z |
|
|
|
ctg iz = −i cth z , |
cth iz = −i ctg z |
|
С учётом приведённых свойств можно получить и две следующие формулы |
||||
|
|
sin(x ±iy) = sin xch y ±i cos xsh y |
|
|
|
|
cos(x ±iy) = cos xch y i sin xsh y |
|
|
Примеры. |
|
|
||
1. Вычислим cos(1+ |
|
i). Применяя формулы из п. 8.1 |
(по сути, хорошо известные |
|
3 |
||||
формулы), получим: cos(1+
 3i)= cos1 cos(i
3i)= cos1 cos(i
 3)−sin1 sin (i
3)−sin1 sin (i
 3)= cos1 ch
3)= cos1 ch
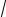 3 −i sin1 sh
3 −i sin1 sh 
 3 .
3 .
Оглавление Е.Е. Красновский, В.Д. Морозова «Теория функций комплексного переменного»

17
2.Вычислим sin 1+ π i .
3
|
π |
|
= sin1cos |
|
π |
+cos1sin |
|
π |
= sin1ch |
π |
+i cos1sh |
π |
. |
||
Аналогично, sin 1+ |
3 |
i |
i |
3 |
|
i |
3 |
|
3 |
3 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|||||
3. Представим в |
алгебраической форме |
значение sh (1− |
3i). Учитывая формулу |
|||||||||||
sh (α −β)= shα chβ −chα shβ |
и формулы |
связи между |
тригонометрическими и |
|||||||||||
гиперболическими функциями, |
найдём |
|
|
|
|
|
|
|
|
|||||
sh (1−i |
|
|
)= sh1 ch (i |
|
)−ch1 sh (i |
|
)= cos |
|
sh1−isin |
|
ch1. |
|||
|
3 |
3 |
3 |
3 |
3 |
|||||||||
4. Аналогично можно вычислить и следующее:
ch (−1−2i)= ch (−1) ch (−2i)+sh (−1) sh (−2i)= cos 2 ch1+i sin 2 sh1.
8.5 Логарифмическая функция
|
Если eω = z , то ω называют логарифмом комплексного числа z и обозначают ω = Ln z . |
||||||||||||||||||||||||||||||||
|
Логарифм |
|
комплексного |
числа |
– |
|
это |
многозначная |
|
|
|
функция |
|||||||||||||||||||||
Ln z = ln |
|
z |
|
+iArg z = ln |
|
z |
|
+i(arg z +2kπ) , |
k Z , в которой мнимая часть определена с точностью |
||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||
до слагаемого кратного 2π . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
Главное значение логарифма ln z |
отвечает значению k = 0 и имеет вид ln z = ln |
|
z |
|
+i arg z . |
|||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||
|
Пример. |
|
Представить |
в |
|
алгебраической |
|
форме |
значение |
|
ln (1+i). |
|
|
|
Поскольку |
||||||||||||||||||
|
|
|
|
|
π |
|
π |
|
1+i |
|
|
|
|
и arg (1+i) |
|
π |
|
ln (1+i)= ln |
|
|
π |
i . Соответственно, |
|||||||||||
1 |
|
|
|
+i sin |
|
= 2 |
|
= |
, то |
2 + |
|||||||||||||||||||||||
+i = 2 cos |
4 |
4 |
, т.е. |
|
|
4 |
4 |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Ln (1+i)= ln 
 2 +i π4 +2kπ , где k .
2 +i π4 +2kπ , где k .
8.6 Общая показательная и общая степенная функции
Можно говорить о возведении комплексного числа в произвольную комплексную степень. По определению полагают, что az = ez Ln a , a ≠ 0 . При фиксированном a ≠ 0 это соотношение определяет, как говорят, общую показательную функцию. Как и в случае логарифма, выделяют
главное значение показательной функции a z , равное ez ln a . Значение, заданное равенством az = ez Ln a , иногда называют общим значением показательной функции.
Оглавление Е.Е. Красновский, В.Д. Морозова «Теория функций комплексного переменного»
