
Сборник задач
.pdf
Максимальное значение КПД достигается при uv = 12 :
1 |
|
cos β |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
ηmax = 2 |
1 + |
1 + |
ζ! . |
||||
Считая процесс идеальным (ζ = 0) , получим для теоретическо- |
||||||||||||||||||||||
го КПД ηт, учитывающего только потерю выходной кинетической |
||||||||||||||||||||||
энергии (определяемой скоростью v2), |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
ηт = 2 (1 + cos β) 1 − |
u |
|
u |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
; |
|
|
|
||||||||||||
|
|
|
v |
v |
|
|
|
|||||||||||||||
|
|
|
ηт max = |
|
1 + cos β |
. |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
При β = 0 (струя отклоняется в относительном движении на |
||||||||||||||||||||||
угол 180◦) получим η |
max |
= 1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
При установившемся |
движении жидкости в равномерно враща- |
|||||||||||||||||||||
ющемся канале динамический реактивный момент действия пото- |
||||||||||||||||||||||
ка на стенки канала относительно оси его вращения определяет- |
||||||||||||||||||||||
ся изменением секундного момента количества движения потока |
||||||||||||||||||||||
(рис. 13.9): |
|
M = ρQ(r1vи1 − r2vи2 ), |
|
|
|
|
|
|
(13.15) |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||
где r1 и r2 – радиусы вращения центров входного и выходного се- |
||||||||||||||||||||||
чений канала; vи1 = v1 cos α1 и vи2 = v2 cos α2 – окружные соста- |
||||||||||||||||||||||
вляющие абсолютных скоростей потока v1 и v2 |
на входе и выходе |
|||||||||||||||||||||
из канала. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
При M > 0 момент действия потока на стенки направлен в сто- |
||||||||||||||||||||||
рону вращения канала (турбина), при M < 0 – |
против вращения |
|||||||||||||||||||||
(насос). Уравнение Бернулли для относительного движения жидко- |
||||||||||||||||||||||
сти в рассматриваемом случае имеет вид |
|
|
|
|
|
|
|
|||||||||||||||
|
p1 |
w12 |
u12 |
|
|
|
p2 |
|
w22 |
u22 |
+ hп, |
(13.16) |
||||||||||
z1 + |
|
+ |
|
− |
|
= z2 + |
|
|
+ |
|
− |
|
|
|||||||||
ρg |
2g |
2g |
ρg |
2g |
2g |
|||||||||||||||||
где относительные скорости w1 и w2 |
в канале связаны уравнением |
|||||||||||||||||||||
расхода |
|
|
|
w1F1 = w2F2, |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
а потеря напора может быть выражена как hп = |
ζw2 |
. |
|
|||||||||||||||||||
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2g |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
401 |

|
Рис. 13.9 |
Рис. 13.10 |
|
Вектор абсолютной скорости жидкости vˉ равен геометрической |
|
сумме ее относительной скорости wˉ |
и переносной скорости канала |
|
uˉ |
и является замыкающей стороной треугольника скоростей: |
|
vˉ = wˉ + uˉ.
В качестве примера определим момент действия потока на рав номерно вращающуюся трубку для которой заданы выходной ра- диус и выходной угол β при постоянном( статическом напоре ис- теченияr сегнерово колесо) рис - По формулеН ( учитывая, . 13что.10)начальный. момент количе ства движения потока(13.15),в баке равен, нулю получим величины в вы- ходном сечении 2 трубки обозначены без, индекса) ( -
M = −ρQrvи.
Если и реактивный момент является движущим напра влен в сторонуv < 0вращения, трубки). Так как из плана скоростей( -
то
M = ρQr (w cos β − u) ,
где расход в трубке площадь сечения трубки По фор муле (13.16) имеем Q = wf (f – ). -
H = w2 (1 + ζ) − u2 2g
402

и |
|
|
|
|
|
|
|
|
|
|
w = ϕp |
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
(13.17) |
|||||||||
где ϕ = |
|
|
|
|
1 |
|
|
|
|
|
2gH + u2 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
– коэффициент скорости трубки. |
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
1 + ζ |
|
|
||||||||||||||||||||||||||||||||||
Для идеального процесса |
(ζ = 0) момент действия потока на |
||||||||||||||||||||||||||||||||||||||
трубку |
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Mт = ρfr h 2gH + u2 cos β − up |
|
|
|
|
|
|
i . |
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
2gH + u2 |
|
|||||||||||||||||||||||||||||||||||
Обозначив v0 = √ |
|
|
|
|
и Q0 = v0f (v0 и Q0 – |
скорость и расход |
|||||||||||||||||||||||||||||||||
2gH |
|||||||||||||||||||||||||||||||||||||||
при и = 0), |
получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u |
|
|
|
|
|
u2 |
|
||||||||||
Mт = ρQ0v0r " 1 + |
|
cos β − |
|
|
|
|
s1 + |
|
# . |
(13.18) |
|||||||||||||||||||||||||||||
v02 |
v0 |
v02 |
|||||||||||||||||||||||||||||||||||||
Момент на заторможенной трубке |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
Mт0 = ρQ0v0r cos β. |
|
|
|
|
|
|
|
|
|
(13.19) |
||||||||||||||||||
Полезная механическая мощность, развиваемая потоком на вра- |
|||||||||||||||||||||||||||||||||||||||
щающейся трубке, Nт |
= Mт ω и теоретический КПД процесса |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
Mт ω |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
ηт = |
|
|
u |
cos βs1 + |
u2 |
|
|
|
u |
! . |
|
(13.20) |
||||||||||||||||||||||||||
|
|
= 2 |
|
|
|
|
|
|
− |
|
|
||||||||||||||||||||||||||||
|
QρgH |
v0 |
v02 |
v0 |
|
||||||||||||||||||||||||||||||||||
Исследование полученного выражения показывает, что теорети- |
|||||||||||||||||||||||||||||||||||||||
ческий КПД достигает максимального значения: η1 max = 1 − sin β |
|||||||||||||||||||||||||||||||||||||||
при соотношении скоростей |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
u |
1 |
sin |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
= s |
|
2−sin ββ |
. |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
v0 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Можно видеть, что движущий реактивный момент на трубке |
|||||||||||||||||||||||||||||||||||||||
(которому отвечают турбинные режимы – получение полезной ра- |
|||||||||||||||||||||||||||||||||||||||
боты за счет уменьшения энергии потока) |
возникает только при |
||||||||||||||||||||||||||||||||||||||
углах выхода β < 90◦. |
Значениям |
β ≥ 90◦ соответствуют насосные |
|||||||||||||||||||||||||||||||||||||
режимы – |
реактивный момент потока направлен противоположно |
||||||||||||||||||||||||||||||||||||||
угловой скорости трубки (М < 0) |
и для ее вращения затрачивается |
||||||||||||||||||||||||||||||||||||||
внешняя работа, идущая на увеличение энергии жидкости. |
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
403 |
ЗАДАЧИ |
|
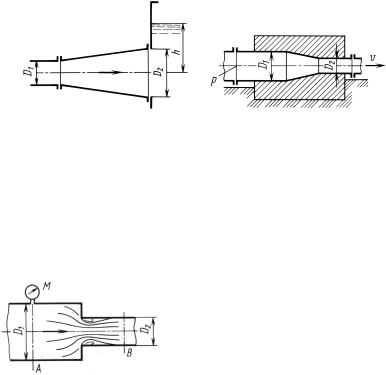
Задача 13.1. Из диффузора, входной и выходной диаметры ко- |
|
торого D1 = 250 мм и D2 = 500 мм, |
вода поступает в бак с посто- |
янным уровнем h = 4 м в количестве |
Q = 0, 4 м3/с. |
1. Определить осевую силу R, действующую на диффузор (ко- |
|
эффициент потерь в диффузоре ϕд = 0, 25). |
|
2. При каком вакууме pв над уровнем воды в баке искомая сила |
|
будет равна нулю? |
кПа. |
Ответ. 1. R = 4,61 кН. 2. рв = 31,4 |
|
К задаче 13.1 |
|
|
|
|
К задаче 13.2 |
|
|||
Задача 13.2. |
Диаметр трубопровода на участке заделки в опору |
||||||||
изменяется от D1 = 1,5 |
м до |
D2 = 1 м. |
|
|
|
||||
Определить осевую силу, |
воспринимаемую опорой на переход- |
||||||||
ном участке при избыточном давлении перед опорой р = 0,4 МПа |
|||||||||
и расходе воды Q = 1,8 |
м3/с. |
|
|
|
|
|
|
|
|
Потерями в конусе пренебречь. |
|
|
|
|
|||||
Ответ. R = 392 кН. |
|
|
Задача |
13.3. |
Определить осевую |
||||
|
|
|
|
||||||
|
|
силу, |
приложенную к трубопроводу |
||||||
|
|
на участке |
AВ внезапного сужения от |
||||||
|
|
D1 |
= 300 |
мм до D2 |
= 200 |
мм. Пока- |
|||
|
|
зание |
манометра |
перед |
сужением |
||||
К задаче 13.3 |
M = 0,15 |
МПа, |
расход воды Q = |
||||||
= |
0,28 м3/с. Сопротивление участка |
||||||||
определить по формуле |
(7.5), |
см. |
гл. 7. |
|
|
|
|
||
Ответ. R = 5 870 Н. |
|
|
|
|
|
|
|
|
|
Задача 13.4. |
На поршень гидроцилиндра диаметром D = 60 мм |
||||||||
действует сила |
Р = 3 000 Н, |
вызывающая |
истечение |
масла из |
|||||
404 |
|
|
|
|
|
|
|
|
|

цилиндра |
через |
торцевое |
отверстие |
|
||
с острой |
кромкой, диаметр |
которого |
|
|||
d = 20 мм. Пренебрегая трением порш- |
|
|||||
ня, |
определить силу, действующую на |
К задаче 13.4 |
||||
цилиндр. |
|
|
|
|||
|
|
Коэффициенты истечения для отверстия принять ϕ = 0,97 и |
||||
μ = 0,63; относительная плотность масла |
δ = 0,9. |
|||||
|
|
Ответ. R = 2 620 Н. |
|
|
||
|
|
Задача |
13.5. |
Расход воды в отсасывающей трубе гидротур- |
||
бины, представляющей вертикальный тонкостенный конический |
||||||
диффузор с диаметрами d = 1 000 мм и |
D = 2 000 мм и длиной |
|||||
L = 4 000 мм, равен Q = 5,5 м3/с. Входное сечение трубы располо- |
||||||
жено выше уровня на Н = 3 м. Коэффициент потерь в диффузоре |
||||||
ϕ |
д |
= 0,25. |
|
|
|
|
|
Определить гидравлическую осевую силу, действующую на |
|||||
трубу. |
|
|
|
|
||
|
|
Указание. Принять, что давление в выходном сечении трубы равно |
||||
статическому давлению в окружающей неподвижной жидкости и что на |
||||||
внешней поверхности трубы, погруженной под уровень, давление распре- |
||||||
делено по статическому закону. |
|
|
||||
|
|
Ответ. R = ρQ (v1 − v2)−pвF +G, где pв – вакуум на входе в трубу; |
||||
G – |
вес воды в трубе над свободной поверхностью. R = 35 кН. |
|||||
|
|
Задача |
13.6. |
Определить гидравлические нагрузки болтовых |
||
групп во фланцевых соединениях А и В |
при истечении воды из |
|||||
бака через отвод и присоединенный к нему насадок. Выходной диа- |
||||||
метр насадка d = 50 мм, диаметр отвода D = 100 мм и его радиус |
||||||
кривизны r = 400 мм. Избыточное давление в баке М = 1 МПа. |
||||||
Гидравлическими сопротивлениями и весом жидкости в отводе |
||||||
пренебречь. |
|
|
|
|||
|
|
Как изменится нагрузка болтов B, если удалить насадок? |
||||
|
|
Ответ. |
Соединение A: отрывающая сила |
PA = 4 450 Н. Соединение |
||
В: отрывающая сила PB = 8 350 |
Н; срезающая сила TB = 3 930 Н; изги- |
|||||
бающий момент MB = 1 570 Н ∙ м. |
|
|||||
|
|
При удалении насадка РB = TB = 15 700 Н; MB = 6 280 Н ∙ м. |
||||
|
|
|
|
|
|
405 |
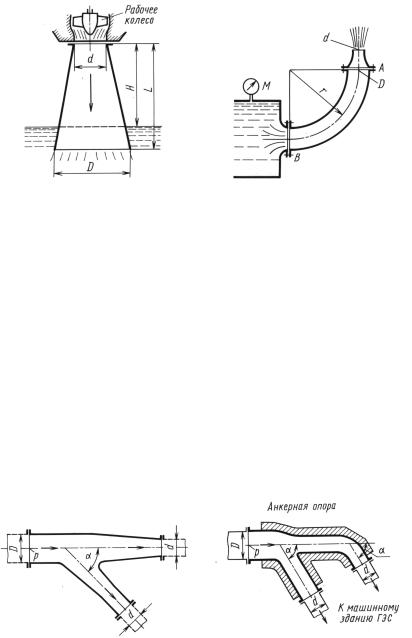
К задаче 13.5 |
К задаче 13.6 |
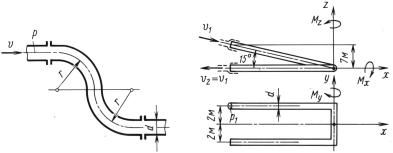
Задача 13.7. Трубопровод ГЭС, имеющий диаметр D = 1,2 м, |
|
разветвляется в горизонтальной плоскости на две линии диаметром |
|
d = 0,85 м, подводящие воду к двухколесной гидротурбине. |
|
Определить силу, воспринимаемую тройником, если боковая |
|
ветвь образует с осью трубопровода угол |
α = 45◦, избыточное да- |
вление перед тройником р = 5 МПа и суммарный расход Q = 6 м3/с |
|
делится поровну между отходящими ветвями. Гидравлическими |
|
сопротивлениями в тройнике пренебречь. |
|
Как изменится эта сила, если при выключении турбины рас- |
|
ход станет равным нулю, а давление в тройнике возрастет до р = |
|
= 7 МПа? |
|
Ответ. R = 2 180 и 3 020 кН. |
|
Задача 13.8. Определить усилие, передающееся на трубопровод |
|
ГЭС в пределах анкерной опоры, расположенной перед машинным |
|
зданием. Диаметр трубопровода D = 3 м, |
а патрубков, подводящих |
К задаче 13.7 |
К задаче 13.8 |
406
воду к турбинам, d = 2 м; |
угол патрубков с осью трубопровода |
|
α = 60◦. Избыточное давление перед опорой |
= 295 кПа и рас- |
|
ход Q = 35 м3/с (делится между патрубками |
поровну). Потерями |
|
напора в пределах опоры пренебречь. |
|
|
Ответ. R = 2 150 кH. |
|
|
Задача 13.9. По отводу типа «утка», диаметр которого d = |
||
= 200 мм и радиус закругления r = 600 мм, течет вода в количестве |
||
Q = 125 л/с. Избыточное давление в отводе р = 200 кПа. |
||
Пренебрегая потерей напора и силой тяжести воды, определить |
||
момент М сил действия потока, воспринимаемый отводом. |
||
При каком вакууме рв этот момент окажется равным нулю? |
||
Ответ. M = 8 140 H ∙ м; |
в = 15,9 кПа. |
|
Задача 13.10. Определить результирующую силу R и моменты |
||
относительно осей х, у и z, возникающие от потока воды на колен- |
||
чатой трубе, размеры которой указаны на рисунке (диаметр трубы |
||
d = 400 мм). Средняя скорость воды v = 3 |
м/с, избыточное да- |
|
вление при входе в трубу p1 = 0,2 МПа. Коэффициент сопротивле- |
||
ния трения λ = 0,02; коэффициент сопротивления каждого колена |
|
ζ = 1,3. Учитывать вес жидкости в трубе. |
кH ∙м; Mz = 13 кH ∙м. |
Ответ. R = 93 кН; Mx = 16 кH ∙м; My = 800 |
|
К задаче 13.9 |
К задаче 13.10 |
|
Задача 13.11. По прямому длинному трубопроводу диаметром |
||
D = 200 мм вода вытекает в атмосферу под напором Н = 16 |
м. |
|
Определить гидравлическую осевую силу, воспринимаемую |
||
трубопроводом. |
|
прене- |
Указание. Имея в виду, что трубопровод является длинным, |
||
бречь сопротивлением входа и скоростным напором выхода, принимая, |
||
что потеря напора на трение по длине трубопровода равна напору |
Н . |
|
|
|
407 |
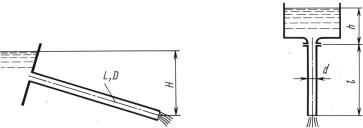
К задаче 13.11 |
|
К задаче 13.12 |
|||||||||||
Ответ. R = ρg |
|
πD2 |
H = 4 930 Н независимо от наклона (длины L) |
||||||||||
|
|
|
|||||||||||
трубопровода. |
4 |
|
|
|
|
|
|
|
|
||||
Задача 13.12. Из бака, в котором поддерживается заданный уро- |
|||||||||||||
вень, жидкость вытекает в атмосферу по вертикальной трубе диаме- |
|||||||||||||
тром d и длиной l. |
|
|
|
|
|
|
|
|
|
|
|||
Найти зависимость гидравлической осевой силы, действующей |
|||||||||||||
на трубу, от уровня h. |
Указать, при каком значении h эта сила будет |
||||||||||||
равна силе тяжести жидкости в трубе. |
|
|
|
|
|||||||||
Сопротивлением входа в трубу пренебречь, коэффициент сопро- |
|||||||||||||
тивления трения λ считать постоянным. |
|
|
|
|
|||||||||
Ответ. R |
|
λ |
|
− 1 lρg |
|
|
|
|
|
||||
|
h |
|
f + G, где f = |
πd2 |
и G = ρdfl. |
||||||||
d |
|
||||||||||||
|
|
|
|
|
|
|
4 |
||||||
|
|
|
1 + λ |
l |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|||
Осевая сила R равнаdсиле тяжести G жидкости в трубе при h = |
d |
. |
|||||||||||
|
|||||||||||||
Задача 13.13. |
|
|
|
|
|
|
|
|
λ |
||||
|
Из насадка, выходной диаметр которого d = |
||||||||||||
= 150 мм, в горизонтальном направлении вытекает струя воды |
|||||||||||||
под напором Н = 125 |
м. |
|
|
|
|
||||||||
Определить мощность струи и силу ее удара о плоскую стенку, |
|||||||||||||
расположенную перпендикулярно к оси струи и под углом α = 60◦. |
|||||||||||||
Коэффициент сопротивления насадка |
ζ = 0,04; сжатие на вы- |
||||||||||||
ходе отсутствует. |
|
|
|
|
|
|
|
|
|
|
|||
Ответ. N = 1 000 кВт; R = 41,5 и 35,9 кН. |
|||||||||||||
Задача 13.14. |
Определить гидравлическую силу, воспринима- |
||||||||||||
емую анкерной опорой в которой участок АС трубопровода ГЭС между двумя расширительными, муфтами меняет направление с на клонного (α = 45◦) на горизонтальное при постоянном диаметре-
408
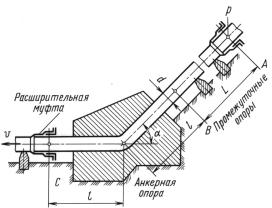
К задаче 13.14
d = 2,5 м. Расход воды Q = 15 м3/с, избыточное давление в начале |
||||
участка р = 0,5 МПа. Гидравлические потери не учитывать. |
||||
Имея в виду, что на длине L = 260 м между сечениями A и В |
||||
установлен ряд промежуточных опор, воспринимающих нормаль- |
||||
ные к оси трубопровода силы, в искомую нагрузку анкерной опоры |
||||
включать на этой длине только осевую составляющую веса воды. |
||||
На участке ВС (l = 20 м) в нагрузку опоры вес воды включать це- |
||||
ликом. |
|
|
|
|
Ответ. Горизонтальная и вертикальная составляющие силы: |
||||
Rгор = (ρQv + p1F ) cos α − (ρQv + p2F ) + GAB |
sin 2α |
; |
||
|
||||
2 |
||||
где p1 и p2– |
Rверт = (ρQv + p1F ) sin α + GAB sin2 α + GBC, |
|
||
избыточные давления в сечениях A и C; v – скорость воды в |
||||
трубе; F – |
площадь сечения трубы; GAB и GBC – |
вес воды на участках |
||
AB и ВС. Rгор = 4 000 кН, Rверт = 10 000 кН. |
|
|
|
|
Полная сила R = 10 800 кН действует вправо вниз под углом 68◦ к |
||||
горизонту. |
|
|
|
|
Задача 13.15. Лафетный пожарный ствол диаметром D = 75 мм, |
||||
снабженный спрыском (насадком) выходным диаметром d = 38 мм, |
||||
работает под избыточным давлением воды |
= 0,8 МПа. |
Опреде- |
||
лить силу воспринимаемую лафетом и разрывающие нагрузки соединения, спрыска со стволом 1 и соединения, ствола с гибким
409
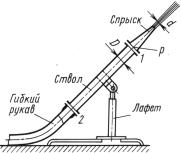
|
|
рукавом 2. Весом жидкости в лафе- |
||
|
|
те пренебречь, коэффициенты исте- |
||
|
|
чения для спрыска |
ε = 1, ζ = 0,06. |
|
|
|
Указание. Сила, действующая на |
||
|
|
спрыск и воспринимаемая соединени- |
||
|
|
ем 1, |
|
|
|
|
P1 = ρQ(v1 − v2) + pF, |
|
|
|
|
где v1 и v2 – скорости в стволе и на вы- |
||
К задаче 13.15 |
ходе из спрыска; F – |
площадь ствола. |
||
Сила, воспринимаемая соединени- |
||||
ем 2, определяется как реакция потока на конец гибкого рукава, примыка- |
||||
ющий к стволу: |
P2 = ρQv1 + pF. |
|
|
|
|
|
|
|
|
Нa лафет передается сила |
|
|
||
|
|
P = P2 − P1 = ρQv2, |
|
|
равная динамической реакции струи, вытекающей из спрыска. |
Н. |
|||
Ответ. |
Усилие на лафете P = 1 820 Н; Р1 = 2 180 |
Н; P2 = 4 000 |
||
Задача |
13.16. Гидромонитор с входным диаметром D1 |
= |
||
= 260 мм и насадком |
(d = 100 мм) работает при горизонтальном |
|||
расположении ствола под избыточным давлением |
= 1,2 МПа. |
|||
Определить усилия, воспринимаемые горизонтальным шарни- |
||||
ром 1, соединением 2 |
ствола с коленом и соединением 3 ствола с |
|||
насадком. |
|
|
|
|
Входной диаметр насадка D2 = 150 мм, длины: L1 = 3 000 мм |
||||
и L2 = 2 300 мм, радиус кривизны колена r = 400 |
мм. |
|
||
Весовыми нагрузками пренебречь, учитывать потери в насадке, |
||||
для которого ζ = 0,1 (сжатие на выходе отсутствует). |
|
|||
Указание. Горизонтальный шарнир воспринимает вертикальную от- |
||||
рывающую силу P1 = ρQv1 + pF, срезающую силу T1 = ρQv3 и изги- |
||||
бающий момент М1 = T1r (v1 и v3 – скорости в колене и на выходе из |
||||
насадка, F – |
площадь колена). |
|
|
|
Соединение ствола с коленом воспринимает отрывающую силу
P2 = ρQ(v1 − v3) + pF.
410
