
Сборник задач
.pdf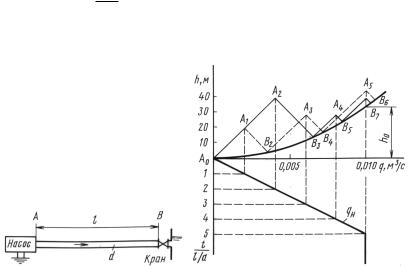
Задача 12.29. На конце трубы, присоединенной к резервуару |
||||||||
большой емкости, установлен кран, открытый настолько, что его ко- |
||||||||
эффициент расхода |
μ0 = 0,48. Напор перед краном h0 = 50 м, дли- |
|||||||
на трубы l = 160 м, диаметр d = 100 мм, скорость ударной волны |
||||||||
а = 770 м/с. Производится мгновенное частичное закрытие крана, |
||||||||
при котором новое значение коэффициента расхода μ1 = 0,016. |
||||||||
Определить максимальное значение ударного напора |
hуд и по- |
|||||||
строить зависимость расхода через кран и напора перед ним по вре- |
||||||||
мени. |
hуд = 60 м. |
|
|
|
|
|||
Ответ. |
|
|
|
|
||||
Задача |
12.30. К насосу подключен горизонтальный трубопро- |
|||||||
вод длиной l = 12 |
м, диаметром d |
= 125 мм с краном на конце. |
||||||
Кран частично открыт так, что его коэффициент расхода |
μ = 0,031. |
|||||||
При включении насоса его подача нарастает по прямой от ну- |
||||||||
ля до q0 = 10 л/с за время t = 0,05 с. Скорость ударной волны |
||||||||
а = 1 200 м/с. Определить закон изменения давления у насоса (се- |
||||||||
чение A) по времени. Трением в трубе пренебречь. |
|
|||||||
Решение. Наносим на график закон изменения подачи насоса qн по |
||||||||
времени, взяв за единицу времени |
l |
= |
12 |
|
= 0,01 с, и параболу расхода |
|||
|
|
|
||||||
через кран qк = μfтр√2gh. Ударные характеристики проводим с угловым |
||||||||
коэффициентом gfтр |
|
a |
1 200 |
масштаб расходов; β, м/мм, |
||||
β , где α, м3/(с ∙ мм), – |
||||||||
|
a |
α |
|
|
|
|
||
масштаб напоров
– Точки A1, A2, A. 3, . . . определяют напор в сечении А в моменты вре-
мени 1, 2, 3, . . . Из графика видно, что напор в этом сечении стремится к
К задачам 12.30 и 12.31 |
К решению задачи 12.30 |
391
значению h0 = 36 м, определяемому из уравнения расхода через кран для |
|||
установившегося режима работы: q0 = μfтр√2gh0 = 10 л/с. |
|||
Задача 12.31. |
Каким будет максимальный ударный напор в се- |
||
чении А у насоса в предыдущей задаче, если принять, что расход |
|||
насоса qн возрастает мгновенно от нуля до 0,010 м3/с и остается в |
|||
последующем постоянным. Найти максимальный расход жидкости |
|||
через кран. Трением в трубе пренебречь. |
|||
Ответ. hA = 100 м и сохраняется постоянным на отрезке времени |
|||
от 0 до 0,02 с; qmax = 0,0135 м3/с и сохраняется постоянным на отрезке |
|||
времени от 0,01 до 0,03 с. |
|
||
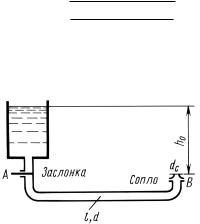
Задача 12.32. |
Труба длиной l = 400 м и диаметром d = 110 мм |
||
с соплом dc = 63 |
мм на конце заполнена водой. Напор h0 = 90 м, |
||
коэффициент расхода сопла μc |
= 0,98, скорость ударной волны в |
||
трубе а = 1 390 м/с. В сечении |
A производится неполное мгновен- |
||
ное открытие заслонки, так что ее коэффициент расхода становится |
|||
равным μз = 0,322. |
|
||
Найти графическим путем закон изменения расхода через соп- |
|||
ло qс по времени. |
Указать установившееся значение qуст расхода, к |
||
которому стремится qс. Трением в трубе и скоростным напором в |
|||
ней пренебречь. |
|
|
|
Указание. |
Параболу потерь напора в заслонке откладывать на графи- |
||
ке от уровня h0 |
вниз, а параболу напора в сечении В перед соплом вверх |
||
от линии h = 0 (от оси расходов). |
|
||
s
Ответ. qуст = μcfc μзfтр (μ f )2 + (μзfтр)2 = 9, 1 л/с.
Задача В условияхc предыдущейc задачи произведено мгновенное 12полное.33. открытие заслонки А. При каком отношении
К задачам 12.32 и 12.33
392

площадей сопла и трубы fc максимальная величина напора в се- чении В перед соплом составитfтр :
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1) h0; 2) |
|
h0; 3) 2h0 |
? |
|
|
|
|
|
|
|||||||||
2 |
|
|
||||||||||||||||
Каковы будут при этом установившиеся значения расхода через |
||||||||||||||||||
сопло qуст? |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Трением в трубе пренебречь. |
|
|
||||||||||||||||
Указание. |
|
Построив схематический чертеж графического решения, |
||||||||||||||||
вычислить требуемые величины аналитически. |
|
|||||||||||||||||
Ответ. 1) |
|
|
|
|
√ |
|
|
|
|
|
= 0, 0154, |
qуст = 6 л/c; |
||||||
|
fc |
|
= |
2gh0 |
|
|||||||||||||
|
fтр |
|
|
|
|
|
||||||||||||
|
|
|
|
2aμc |
|
|
||||||||||||
|
|
|
|
|
√ |
|
|
|
|
|
qуст = 2, 46 л/с; |
|||||||
2) |
|
fc |
|
2gh0 |
||||||||||||||
|
|
|
= |
2√ |
|
aμc |
= 0, 0063, |
|||||||||||
|
fтр |
|||||||||||||||||
|
|
|
6 |
|||||||||||||||
3) |
|
fc |
|
= 0, |
|
|
|
qуст = 0. |
|
|
||||||||
|
fтр |
|
|
|
|
|
||||||||||||
|
|
|
На конце трубы, заполненной водой, находится в |
|||||||||||||||
Задача 12.34. |
||||||||||||||||||
неподвижном состоянии поршень. Начальное избыточное давление |
||||||||||||||||||
в трубе равно нулю. |
Масса т, движущаяся со скоростью v0, ударяет |
|||||||||||||||||
в шток поршня, после чего поршень и масса |
движутся как одно |
|||||||||||||||||
тело Вследствие большой длины трубы и вязкости жидкости отра женные. волны не доходят до поршня Определить закон изменения- давления перед поршнем и закон движения. поршня в функции вре мени Трением поршня о стенки трубы и его массой пренебречь- Скорость. ударной волны в трубе равна а. .
|
|
|
К задаче 12.34 |
|
|
|
|
|
||
Указание. Воспользоваться формулой Жуковского в дифференциаль- |
||||||||||
ной форме dp = ρadv. |
aρf |
|
t; x = aρfп 1 − e− |
aρf |
|
t |
, где fп – |
пло- |
||
Ответ. p = aρv0e− |
m |
п |
m |
п |
||||||
щадь поршня. |
|
|
|
v0m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Глава ВЗАИМОДЕЙСТВИЕ ПОТОКА 13. С ОГРАНИЧИВАЮЩИМИ
ЕГО СТЕНКАМИ ГИДРАВЛИЧЕСКИЕ. МАШИНЫ
ВВЕДЕНИЕ
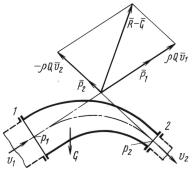
Результирующая сила действия потока на стенки неподвиж ного канала реакция потокаR при установившемся движении жид- кости определяется( по теореме) количества движения векторным- уравнением (рис. 13.1)
|
ˉ |
ˉ |
|
ˉ |
ˉ |
|
|
(13.1) |
|
R = ρQvˉ1 |
− ρQvˉ2 + P1 + P2 |
+ G, |
|
|
|||
|
|
где ρQvˉ1 |
и ρQvˉ2 |
– |
|
векторы се- |
||
|
|
кундных количеств |
движения по- |
|||||
|
|
тока, |
т. е. |
количеств движения |
||||
|
|
массы |
жидкости, |
|
протекающей |
|||
|
|
в единицу времени через вход- |
||||||
|
|
ное и выходное сечения канала |
||||||
|
|
(Q – расход; |
ρ – плотность жид- |
|||||
|
|
кости; v1 и v2 – средние скорости |
||||||
|
|
|
|
|
|
ˉ |
|
ˉ |
|
|
в этих сечениях); P1 |
и P2 – силы |
|||||
|
|
давления, |
действующие во вход- |
|||||
Рис |
. 13.1 |
ном и выходном сечениях канала |
||||||
|
на заполняющую |
его жидкость |
||||||
(P1 = p1F1 и P2 = p2F2, где F – площадь соответствующего се-
чения и |
р |
ˉ |
вес |
– давление в центре тяжести этой площади); G – |
|||
жидкости, заполняющей канал. |
|
||
394 |
|
|
|
В этом уравнении вектор |
Rд |
= ρQvˉ1 − ρQvˉ2 – |
динамическая |
||||||||
|
|
|
|
ˉ |
|
|
|
|
|
|
|
слагающая реакции потока на стенки канала, определяемая измене- |
|||||||||||
нием секундного количества движения потока при протекании жид- |
|||||||||||
кости по каналу. Вектор Rст = P1 |
+P2 +G – статическая слагающая |
||||||||||
реакции потока. |
ˉ |
|
ˉ |
ˉ |
ˉ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Уравнение применимо к потоку, который во входном и выход- |
|||||||||||
ном сечениях удовлетворяет условию плавной изменяемости (ма- |
|||||||||||
лая кривизна линий тока и малые углы между ними) и обладает до- |
|||||||||||
статочно равномерным распределением скоростей в этих сечениях. |
|||||||||||
Для определения суммарной силы, |
воспринимаемой стенками |
||||||||||
канала, на несмоченную поверхность которых действует атмосфер- |
|||||||||||
ное давление pат, в формуле (13.1) силы давления P1 и |
P2 |
следует |
|||||||||
определять по избыточным давлениям p |
1 |
= p1−pат |
и pи2 |
= p2−pат. |
|||||||
Если в центре одного из сечений |
имеется |
вакуум |
(p |
< 0) , |
сила из- |
||||||
быточного давления в этом сечении имеет направление, противопо- |
|||||||||||
ложное указанным на рис. 13.1. |
|
|
|
|
|
|
|
||||
Силу |
R можно определить непосредственно геометрическим |
||||||||||
суммированием слагающих ее векторов по уравнению |
(13.1) или |
||||||||||
пользуясь методом проекций на координатные оси. |
В зависимости |
||||||||||
от величины и ориентации слагающих векторов суммарное воздей- |
|||||||||||
ствие потока и внешнего давления на стенки может сводиться к |
|||||||||||
силе, моменту или динаме (динамическому винту). |
|
|
|
||||||||
Если в канале происходит слияние или разделение потоков, сила |
|||||||||||
R определяется из векторного соотношения: |
|
|
|
|
|||||||
|
k |
n |
|
|
k |
|
n |
|
|
|
|
X |
X |
|
|
X |
|
X |
|
ˉ |
|
||
ˉ |
ρQ1ivˉ1i − |
ρQ2ivˉ2i + |
ˉ |
ˉ |
|
(13.2) |
|||||
R = |
P1i + |
P2i + G, |
|||||||||
где k и |
1 |
1 |
|
|
1 |
|
1 |
|
|
|
|
n – число входных и выходных сечений канала соот- |
|||||||||||
ветственно. |
некоторые |
примеры |
|
|
|
|
|
|
|||
Рассмотрим |
|
|
|
|
|
|
|||||
определения реакции потока на стен- |
|
|
|
|
|
|
|||||
ки каналов. |
|
|
|
|
|
|
|
|
|
|
|
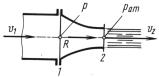
А. Сужающийся насадок с выхо- |
|
|
|
|
|
|
|||||
дом в атмосферу (рис. 13.2). Применяя |
|
|
Рис. 13.2 |
|
|||||||
уравнение (13.1) |
в проекциях на гори- |
|
|
|
|||||||
зонтальную ось насадка, |
получим осевую силу, действующую на |
||||||||||
его стенки: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
395 |

R = pиF1 |
− ρQ(v2 − v1), |
пло- |
|||||
где pи – избыточное давление во входном сечении насадка; F1 – |
|||||||
щадь этого сечения. |
|
|
|
|
|
|
|
Величины, входящие в предыдущую формулу, связаны уравне- |
|||||||
нием Бернулли |
|
|
|
|
|
|
|
|
pи |
+ |
v12 |
= |
v22 |
(1 + ζ) |
|
и уравнением расхода ρ |
|
|
|
||||
2 |
2 |
|
|
||||
Q = v1F1 |
= v2F2, |
|
|
|||
где ζ – коэффициент сопротивления насадка. |
|
после |
||||
Пренебрегая незначительным сопротивлением насадка, |
||||||
преобразований получаем |
|
|
|
|
||
R = ρ |
v22 |
(F1 − F2)2 |
, |
|
|
|
|
|
|
||||
2 |
|
F1 |
|
|
||
где F2 – площадь выходного сечения насадка. |
, в част- |
|||||
Результат справедлив при любом соотношении F1 и F2 |
||||||
ности, также и для расширяющихся насадков (F2 > F1) ; |
во всех |
|||||
случаях сила R направлена к выходному сечению. |
|
|
||||
Б. Диффузор в трубопроводе (рис. 13.3). Сила, воспринимаемая |
||||||
вертикальным диффузором, действует вдоль его оси. Считая поло- |
||||||
жительным направление этой оси вверх, по уравнению (13.1) |
полу- |
|||||
чим |
|
|
|
|
||
R = pи2 F2 − pи1 F1 − ρQ (v1 − v2) − G, |
|
|
||||
где и скорости и избыточные давления во входном
и сечениях
и выходномv1, p 1 v2, p 2 – диффузора и площади этих сечений1 вес жидкости2 в диффузоре ; F1 F2 – ; G – Если то сила направлена. вверх к входному сечению
диффузораR >такой0, случай всегда имеет место( когда давление на входе в диффузор); больше атмосферного , При вакууме во входном сечении сила может изменить(pнаправление1 > 0) . на противо положное R -
Для горизонтального. диффузора осевая сила
R = pи2 F2 − pи1 F1 − ρQ (v1 − v2) .
396
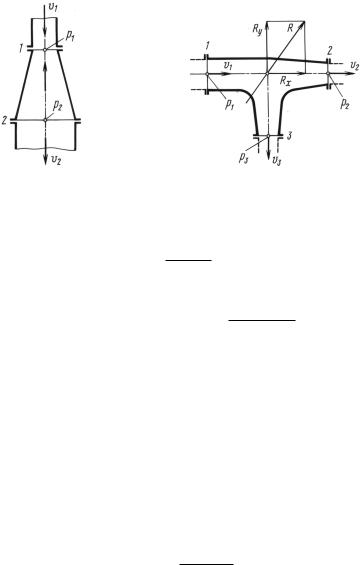
Рис. 13.3 |
|
|
|
|
|
|
|
Рис. 13.4 |
|
||
Пренебрегая потерями, имеем |
|
|
|
|
|
||||||
pи2 = pи1 + ρ |
v12 − v22 |
и Q = v2F2, |
|
||||||||
откуда |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
v12 |
|
(F2 − F1)2 |
|
|
||
R = p |
|
(F F ) + ρ |
|
. |
|
||||||
|
|
|
|||||||||
|
и1 |
2 − |
1 |
2 |
|
F2 |
зна- |
||||
При pи1 = −ρ 21 |
1 − F2 |
получаем R = 0; большим´ |
|||||||||
|
v2 |
|
|
F1 |
|
|
|
|
|
|
|
чениям вакуума отвечает направление силы к выходному сечению |
|||||||||||
диффузора. |
|
|
|
|
|
|
|
|
|
|
|
В. Приточный тройник (рис. 13.4). Пренебрегая весом жидко- |
|||||||||||
сти, для проекций искомой силы на оси ответвлений тройника по- |
|||||||||||
лучаем |
|
|
|
|
|
|
|
|
|
|
|
Rx = pи1 F1 − pи2 F2 + ρQ1v1 − ρQ2v2; |
|
||||||||||
Ry = pи3 F3 + ρQ3v3, |
|
|
|
|
|
||||||
где расход жидкости входящей в тройник и расходы жидкостиQ1 – выходящей из тройника, ; Q2 Q3 –
Полная, сила q (Q1 = Q2 + Q3). R = Rx2 + Ry2.
Соотношения между входным давлением и и выходными да влениями и определяются при заданныхpрасходах по уравне-
Бернулли записанному 1
нию p 2 p 3 для каждого ответвления с учетом его- коэффициента,сопротивления.
397
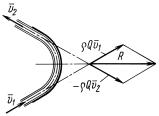
|
|
Сила действия свободной струи на |
|
|
преграду определяется изменением се- |
|
|
кундного количества движения струи, |
|
|
происходящим в результате ее откло- |
|
|
нения преградой. При этом влиянием |
|
|
силы тяжести можно в большинстве |
|
|
случаев пренебречь, получая для дина- |
Рис |
. 13.5 |
мической реакции струи на преграду |
|
(рис. 13.5) следующее выражение: |
ˉ |
− ρQvˉ2, |
(13.3) |
R = ρQvˉ1 |
||
где Q – расход струи; vˉ1 и vˉ2 – векторы скоростей струи перед пре- |
||
градой и после нее. |
|
|
Если струя делится преградой на n частей, то |
|
|
|
n |
|
X |
|
|
ˉ |
ρQ2ivˉ2i. |
(13.4) |
R = ρQvˉ1 − |
||
|
1 |
|
Пренебрегая силой тяжести и гидравлическими сопротивлени- |
||
ями, можно принять, что скорость струи перед преградой и после |
||
нее имеет одинаковое значение (v1 |
= v2) . |
|
При сделанных предположениях сила действия свободной |
||
струи на плоскую стенку, размеры которой велики по сравнению с |
||
диаметром струи (рис. 13.6), |
|
|
R = ρQv sin α = ρF v2 sin α, |
(13.5) |
|
где α – угол наклона стенки к оси струи; F – площадь сечения |
||
струи; v – скорость струи. |
|
|
Для стенки, перпендикулярной к струе, |
|
|
R = ρQv = ρF v2. |
(13.6) |
|
Сила действия струи на симметричную криволинейную стенку, |
||
которая делит струю на две части, отклоняемые на одинаковые углы |
||
γ (γ = 180◦ − β, где β – дополнительный угол выходного элемента |
||
стенки, рис. 13.7), |
|
|
R = γQv (1 − cos γ) = ρQv (1 + cos β) . |
(13.7) |
|
398 |
|
|
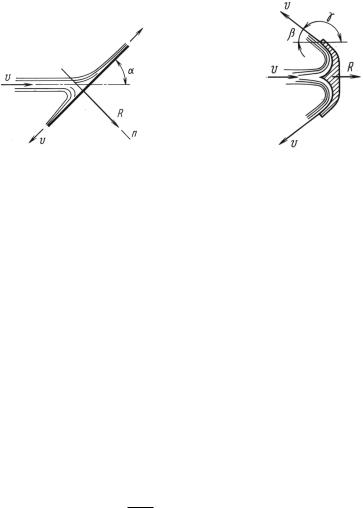
Рис. 13.6 |
|
|
|
|
|
|
|
|
|
|
Рис. 13.7 |
|
|||
Сила получается наибольшей при отклонении струи на угол |
|||||||||||||||
γ = 180◦ : |
|
R = 2 |
ρQv. |
|
|
|
|
|
|
|
|||||
При установившемся движении жидкости в канале, перемеща- |
|||||||||||||||
ющемся прямолинейно и поступательно с постоянной скоростью u, |
|||||||||||||||
сила R определяется из уравнения (13.1), |
в котором динамическая |
||||||||||||||
реакция потока равна изменению его секундного количества дви- |
|||||||||||||||
жения, вычисляемого по отношению к подвижным стенкам: |
|
||||||||||||||
ˉ |
|
|
|
|
|
ˉ |
|
ˉ |
|
ˉ |
(13.8) |
||||
R = ρQwwˉ1 − ρQwwˉ2 + P1 |
+ P2 |
+ G, |
|||||||||||||
где Qw – расход жидкости в канале, Qw |
= w1F1 |
= w2F2; wˉ1 |
и wˉ2 – |
||||||||||||
векторы относительных скоростей во входном и выходном сечениях |
|||||||||||||||
канала. |
|
|
|
|
|
|
|
|
|
|
|
|
|||
Уравнение Бернулли для рассматриваемого случая относитель- |
|||||||||||||||
ного движения жидкости имеет вид |
|
|
|
|
|
|
|
||||||||
z1 + |
p1 |
|
+ |
w12 |
= z2 |
+ |
p2 |
+ |
w22 |
|
+ hп, |
(13.9) |
|||
ρg |
2g |
ρg |
2g |
||||||||||||
|
|
|
|
|
|
|
|
|
|||||||
где потеря напора hп = ζw2 (ζ – коэффициент сопротивления; w – характерная относительная2g скорость
Сила действия свободной струи на). симметричную криволиней ную стенку которая поступательно перемещается в направлении- движения струи, с постоянной переносной скоростью u (рис. 13.8),
R = ρQw (w1 + w2 cos β) , |
(13.10) |
где w1 = v−u – относительная скорость натекания струи на стенку; |
|
Qw = w1F = (v − u) F – |
расход струи по отношению к стенке. |
|
399 |
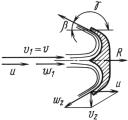
|
Пренебрегая гидравлическими сопроти- |
||||||||
влениями при обтекании стенки, |
получим |
||||||||
относительную скорость отклоненной струи |
|||||||||
w2 = w1 |
и силу действия струи на стенку |
||||||||
|
|
R = ρF (1 + cos β) (v − u)2 . |
|||||||
|
|
|
|
|
|
|
|
ζw22 |
|
Рис. 13.8 |
Учитывая потерю напора hп = |
|
|
, из |
|||||
|
2g |
||||||||
уравнения Бернулли для относительного движения жидкости най- |
|||||||||
дем |
w2 = w2 (1 + ζ) ; |
|
|
|
|||||
|
|
|
|
||||||
|
1 |
|
|
2 |
|
|
|
|
|
при этом сила действия струи |
|
|
|
|
|
|
|
|
|
R = ρF |
1 + |
|
|
cos β |
(13.11) |
||||
|
|
|
1 + ζ! (v − u)2 . |
||||||
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Развиваемая струей полезная механическая мощность N = Ru. |
|||||||||||||||||
КПД, представляющий отношение полезной мощности к затрачи- |
|||||||||||||||||
ваемой мощности струи, определяется выражением |
|
||||||||||||||||
|
Ru |
cos β |
|
|
|
u |
|
2 u |
|
||||||||
η = |
|
|
|
= 2 1 + |
|
|
|
! |
1 − |
|
|
|
|
. |
(13.12) |
||
|
v2 |
|
|
v |
v |
||||||||||||
|
|
1 + ζ |
|
||||||||||||||
|
ρQ |
|
|
|
p |
|
|
|
|
|
|
|
|||||
|
2 |
|
|
|
|
|
|
|
|
||||||||
Если весь расход струи Q = F v используется рядом следую- |
|||||||||||||||||
щих друг за другом лопастей (рабочее колесо активной турбины), |
|||||||||||||||||
то суммарная сила действия струи на лопасти |
! (v − u) v |
|
|||||||||||||||
R = ρQ (w1 + w2 cos β) = ρF 1 + |
|
cos β |
ζ |
(13.13) |
|||||||||||||
|
1 + |
||||||||||||||||
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
и КПД процесса преобразования кинетической энергии струи в по- |
||||||||||||||
лезную механическую работу на колесе (КПД колеса) |
|
|||||||||||||
|
Ru |
|
|
cos β |
|
|
u u |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
p |
|
|
|
|
|
|
|
|
|
η = |
ρQ |
v2 |
|
= 2 |
1 + |
1 + |
ζ! 1 − v v . |
(13.14) |
||||||
400 |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
