
Сборник задач
.pdf
личилась в |
|
y |
раз, а давление под клапаном возросло в |
|
y |
|
2 раз. |
y |
z |
y |
|
z |
|||
Таким образом, если давление под клапаном в положении его равновесия |
|||||||
|
|
− |
|
|
− |
|
|
было р, то при отклонении на величину z от этого положения давление |
|||||||||||||||||||||||||||||||||||||||||
стало |
|
|
|
|
|
|
|
pt = p |
|
y |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
y |
− |
z |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
Можно приближенно считать, что увеличение усилия на клапан со |
|||||||||||||||||||||||||||||||||||||||||
стороны жидкости выражается формулой |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
d2 |
d2 |
|
|
|
y |
|
|
|
|
2 |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Pж = (p1 − p) |
π |
|
|
= p |
π |
|
|
" |
|
|
|
|
|
− 1# . |
|
|
|||||||||||||||||||||||||
4 |
|
|
4 |
|
|
y − z |
|
|
|||||||||||||||||||||||||||||||||
Уменьшение усилия на клапан со стороны пружины при уменьшении |
|||||||||||||||||||||||||||||||||||||||||
его подъема на z |
|
|
|
|
|
|
|
|
|
|
|
|
Pпруж |
= cz. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Восстанавливающая сила, которая возникает на клапане при отклоне- |
|||||||||||||||||||||||||||||||||||||||||
нии от положения равновесия, |
|
|
|
|
|
|
|
|
" |
|
|
|
|
|
|
|
|
|
− 1# + cz. |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d2 |
|
y |
|
2 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
P = |
Pж + |
|
|
Pпруж |
= p |
π |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
4 |
y − z |
|
|
||||||||||||||||||||||||||||||||||||
В положении равновесия клапана |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
πd2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
= c(y0 + y), |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
следовательно, |
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2y |
z |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
P = c (y0 + y) |
" |
|
|
|
|
|
|
− 1# + cz = cz "(y0 + y) |
(y |
−z)2 |
+ 1# . |
||||||||||||||||||||||||||||||
y |
− |
z |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|||||||||
Так как амплитуда колебаний z мала по сравнению с подъемом клапа- |
|||||||||||||||||||||||||||||||||||||||||
на у, то можно приближенно принять 2y − z ≈ 2y |
|
и |
(y − z)2 ≈ y2, тогда |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
( |
y |
0 |
+ y) 2y |
|
|
|
|
|
|
2 |
|
|
3 |
|
|
|
||||||||||||||||||||
P ≈ cz |
|
|
|
|
|
|
|
+ 1 = cy0z |
|
|
+ |
|
. |
|
|
||||||||||||||||||||||||||
|
|
|
y2 |
|
|
|
y |
y0 |
|
|
|||||||||||||||||||||||||||||||
Дифференциальное уравнение движения клапана, масса которого т, |
|||||||||||||||||||||||||||||||||||||||||
имеет вид |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
d2z |
= |
−R − P ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
dt2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
d2z |
|
|
|
|
|
dz |
|
|
|
|
|
|
|
|
2 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
m |
|
+ |
ϑ |
|
|
+ cy0z |
|
+ |
|
= 0, |
|
|
|||||||||||||||||||||||||||||
dt2 |
dt |
y |
y0 |
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
381 |
|
или
d2z + 2Adz + B2z = 0,
где для краткости введеныdt2обозначенияdt
|
|
|
|
|
ϑ |
|
|
|
|
|
cy |
2 |
|
3 |
|
|
|||
|
|
|
|
A = |
|
|
и B2 = |
0 |
|
|
+ |
|
. |
|
|||||
|
|
|
2m |
m |
y |
y0 |
|
||||||||||||
Вычисляя, получаем |
А = 250 с−1; B2 = 92 000 c−2 и период колеба- |
||||||||||||||||||
ний T = |
|
2π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
√ |
|
= 0, 0365 c. Задача 12.15. Система, состоящая |
|||||||||||||||||
B2 − A2 |
|||||||||||||||||||
|
|
|
|
|
|
|
|
из пружины, поршня и столба жидкости |
|||||||||||
|
|
|
|
|
|
|
|
длиной L, выведена из состояния покоя |
|||||||||||
|
|
|
|
|
|
|
|
и совершает свободные колебания. |
|||||||||||
|
|
|
|
|
|
|
|
|
|
Определить период колебаний, если |
|||||||||
|
|
|
|
|
|
|
|
масса поршня |
m и площадь попереч- |
||||||||||
|
|
|
|
|
|
|
|
ного сечения трубки |
F . Режим тече- |
||||||||||
|
|
|
|
|
|
|
|
ния жидкости в трубке считать лами- |
|||||||||||
|
|
|
|
|
|
|
|
нарным: |
|
плотность и кинематическая |
|||||||||
|
|
|
|
|
|
|
|
вязкость жидкости ρ |
и ν. Массой пру- |
||||||||||
|
|
|
|
|
|
|
|
жины пренебречь. |
|
||||||||||
К задаче |
12.15 |
|
|
|
|
|
Сравнить найденный период с пе- |
||||||||||||
|
|
|
|
|
риодом |
колебаний, |
вычисленным в |
||||||||||||
предположении отсутствия трения. |
|
|
|
|
|
|
|
|
|||||||||||
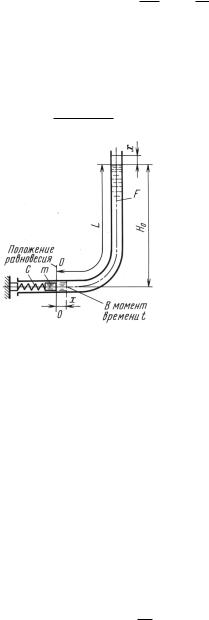
Решение. Пусть в некоторый момент времени t выведенный из поло- |
|||||||||||||||||||
жения равновесия поршень, |
масса которого m, |
двигаясь вправо, находится |
|||||||||||||||||
на расстоянии х от положения равновесия; избыточное давление жидко- |
|||||||||||||||||||
сти на поршень в этот момент равно р. |
Тогда дифференциальное уравне- |
||||||||||||||||||
ние движения поршня имеет вид |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
d2x |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
m |
|
= −cx − pF, |
|
|||||||||||
или |
|
|
dt2 |
|
|||||||||||||||
|
|
|
d2x |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
m |
+ pF + cx = 0, |
(1) |
||||||||||||
|
|
|
|
|
|
|
|
||||||||||||
где с – жесткость пружины. dt2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||
Давление р |
на поршень найдем, применяя уравнение (12.3) для сече- |
||||||||||||||||||
ния у поршня и свободной поверхности в трубке: |
|
||||||||||||||||||
p = H0 + x + hп + hин,
ρg
382

где hп – потеря напора в трубке; для ламинарного течения hп = 8 πνL dx; gF dt
hин – инерционный напор, hин = L d2x.
Подставляя выражения потерьg dtи 2инерционного напора в уравнение Бернулли, получаем
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
πνL dx |
|
L d2x |
|
|
|
|
(2) |
|||||||||
|
|
|
|
|
|
|
= H0 |
|
+ x + 8 gF |
|
+ |
|
|
|
|
|
. |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
ρg |
dt |
g |
dt2 |
|
|
|
|
|
|||||||||||||||||||||||||
Объединяя уравнения (2) и (1), находим дифференциальное уравнение |
||||||||||||||||||||||||||||||||||||||
движения системы |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
(m + ρLF ) |
d2x |
|
|
|
|
πμL dx |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
+ 8 |
|
|
|
|
|
|
|
|
|
|
+ (c + ρgF ) x + |
|
ρgF H0 = 0. |
|
|||||||||||||||||||||
dt2 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
F dt |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Разделив все члены уравнения на m + ρLF, получим |
|
|
||||||||||||||||||||||||||||||||||||
|
d2x |
+ 8 |
πμL |
|
|
|
|
|
dx |
|
|
|
c + ρgF |
x + |
|
|
ρgF H0 |
= 0. |
(3) |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
dt2 |
(m + ρLF ) F |
dt |
m + ρLF |
m + ρLF |
|||||||||||||||||||||||||||||||||
Удобно ввести новую переменную |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ρgF H0 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
s = x + |
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
c + ρgF |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Тогда уравнение (3) преобразуется в однородное линейное дифферен- |
||||||||||||||||||||||||||||||||||||||
циальное уравнение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
d2s |
|
+ 2A |
ds |
+ B2s = 0, |
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
dt2 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
где A = 4(m + ρLF ) F ; B2 = m + ρLF . |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
πμL |
|
|
|
|
|
|
|
|
c + ρgF |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Если B2 > A2, то период колебаний (см. задачу 12.11) |
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
T = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2π |
|
|
|
|
|
|
|
|
|
. |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
s |
c + ρgF |
|
− |
|
4πμL |
|
2 |
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
m + ρLF |
|
(m + ρLF ) F |
|
|
|
|
|
||||||||||||||||||||||||
При отсутствии сопротивления период колебаний
s
m + ρLF T0 = 2π c + ρgF .
383
Выражение T0 можно найти проще, используя аналогию с задачей ме- |
|||||||||||||
ханики о колебаниях груза массой M0, подвешенного на пружине жестко- |
|||||||||||||
стью c0. Период собственных колебаний груза при отсутствии сопроти- |
|||||||||||||
влений, как известно, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T0 = 2πr |
M |
|||||||||
|
|
|
0 |
. |
|
|
|||||||
|
|
|
c0 |
||||||||||
В данном случае массой груза M0 является масса поршня m плюс мас- |
|||||||||||||
са водяного столба ρLF (массой пружины пренебрегаем). Жесткость с0 |
|||||||||||||
равна жесткости пружины |
плюс отнесенное к единице перемещения во- |
||||||||||||
дяного столба изменение |
усилия на поршень вследствие изменения напо- |
||||||||||||
ра H0 при колебаниях: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c0 |
= c + |
xF ρg |
= c + ρgF. |
|||||||||
|
|
|
|
||||||||||
Следовательно, |
|
|
|
x |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T0 |
= 2πs |
m + ρLF |
|||||||||
|
|
|
. |
||||||||||
|
|
c + ρgF |
|||||||||||
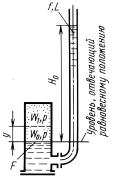
Задача 12.16. Жидкость в трубе, подключенной к воздушному |
|||||||||||||
колпаку поршневого насоса, выведена из положения равновесия. |
|||||||||||||
|
Пренебрегая сопротивлением, определить ча- |
||||||||||||
|
стоту собственных колебаний жидкости, если |
||||||||||||
|
длина трубы, заполненной жидкостью, L, пло- |
||||||||||||
|
щадь ее поперечного сечения f, площадь сече- |
||||||||||||
|
ния колпака F и объем воздуха в колпаке при |
||||||||||||
|
равновесном положении уровней W0. |
||||||||||||
|
|
Высота столба жидкости, соответствующая |
|||||||||||
|
давлению в колпаке в положении равновесия, |
||||||||||||
|
H0 |
. Инерцией жидкости в колпаке пренебречь, |
|||||||||||
|
считая площадь поперечного сечения колпака |
||||||||||||
К задаче 12.16 |
значительно большей, чем площадь попереч- |
||||||||||||
ного сечения трубы. |
|||||||||||||
Решение. Представив находящийся в колпаке воздух как пружину, вы- |
|||||||||||||
числим жесткость c0 |
такой «пневматической пружины». |
||||||||||||
В положении равновесия объем воздуха в колпаке и абсолютное давление р Пусть при отклонении уровня воды вверхWна0 величину у от положения0равновесия. объем воздуха станет и давление
сатьТогда, принимая процесс сжатия газа изотермическимW ,рможем. запи-
pW = p0W0,
384
откуда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
W |
|
W |
|
|
1 |
|
|
|
|
|
F |
|||||
p = p0 |
0 |
= p0 |
0 |
= p0 |
|
|
|
≈ p0 1 + |
|
y . |
|||||||
W |
W0 F y |
1 |
|
|
|
F y |
W0 |
||||||||||
|
|
|
− |
|
− |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
W0 |
|
|
|
|
|
|
||||
Следовательно, увеличение давления p − p0 = W0 . |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F p0y |
|
|
|
Поэтому жесткость «пневматической пружины |
», |
пересчитанная на |
|||||||||||||||
перемещение s воды в трубе, |
|
|
|
ρgH0 |
|
|
|
|
|
||||||||
|
|
c0 = |
(p − p0)Fy |
= |
|
f2, |
|
|
|||||||||
|
|
|
|
|
|||||||||||||
|
|
|
|
s2 |
|
|
|
|
W0 |
|
|
||||||
где s = yF .
Массаf колеблющегося на этой «пружине» груза
|
|
M0 = Lf ρ, |
|||||||||
поэтому частота собственных колебаний жидкости |
|||||||||||
|
|
|
|
|
|
|
|
|
r |
H fg |
|
|
1 |
r |
c |
|
1 |
||||||
n = |
0 |
= |
|
0 |
. |
||||||
2π |
M0 |
2π |
W0L |
||||||||
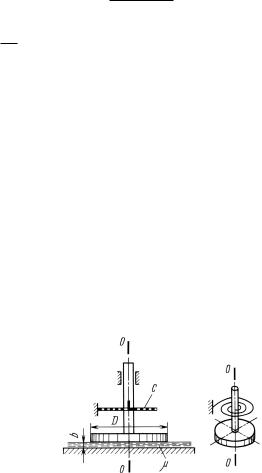
Задача 12.17. Круглый диск (D = 150 мм), к которому в его |
|||||||||||
плоскости приложена и внезапно удалена пара сил, совершает кру- |
|||||||||||
тильные колебания относительно оси О − О. Затухание колеба- |
|||||||||||
ний происходит благодаря трению в вязком слое жидкости по торцу |
|||||||||||
диска. |
|
|
|
|
|
||||||
Пренебрегая массой стержня, определить частоту крутильных |
|||||||||||
колебаний, если масса диска m = 1 |
кг, динамическая вязкость жид- |
||||||||||
кости μ П и толщина жидкого слоя мм Жесткость пру жины с = 1 Н ∙ м рад b = 0,5 . -
= 0,1 / .
К задаче 12.17
385
Течение в вязком слое считать ламинарным
Указание. Дифференциальное уравнение колебаний. имеет вид
|
|
|
|
|
J |
d2 ϕ |
|
+ ϑ |
dϕ |
+ cϕ = 0, |
|
|
|||||||||
где J – |
|
|
|
dt2 |
|
dt |
|
|
угол закру- |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
момент инерции диска относительно оси О − О;4 |
ϕ – |
||||||||||||||||||||
чивания диска; ϑ – |
фактор демпфирования: ϑ = |
π |
μ |
D |
; c – |
жесткость |
|||||||||||||||
|
|
|
|||||||||||||||||||
пружины. |
|
|
|
|
|
|
|
|
|
|
|
|
|
16 b |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Ответ. |
Частота колебаний n = 2πr |
|
|
|
|
|
= 0, 78 Гц. |
|||||||||||||
|
|
J |
− 4J2 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
c |
|
ϑ2 |
|
|
|||||
да |
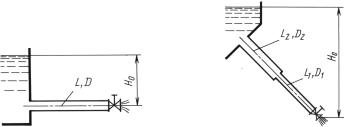
Задача 12.18. Затвор, установленный на конце трубопрово- |
||||||||||||||||||||
(L = |
100 |
м; |
D = 100 мм), работающего под напором во- |
||||||||||||||||||
ды |
Н0 |
= |
10 |
м, |
уменьшает расход от его начального значения |
||||||||||||||||
Q0 |
= 10 л/с до нуля за время Т = 1 с. |
|
|
|
|
|
|
|
|
||||||||||||
|
Принимая закон закрытия затвора линейным и считая трубопро- |
||||||||||||||||||||
вод и жидкость неупругими, определить максимальное повышение |
|||||||||||||||||||||
давления в трубопроводе в процессе закрытия. |
|
|
|||||||||||||||||||
|
Потерями напора в трубопроводе пренебречь. |
|
|
||||||||||||||||||
|
Ответ. |
pин = 0,24 МПа. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
К задаче 12.18 |
К задаче 12.19 |
|
Задача |
12.19. Затвор, установленный в конце трубопровода, со- |
|
стоящего из двух участков (L1 |
= 50 м; D1 = 100 мм и L2 = 50 м; |
|
D2 = 120 мм), закрываясь по линейному закону, уменьшает расход |
||
воды от Q0 = 15 л/с до Q1 = 5 |
л/с в течение Тз = 1 с. Располагае- |
|
мый напор |
Н0 = 40 м. |
|
Определить максимальное повышение давления в трубопрово- |
||
де в процессе закрытия, считая его стенки и жидкость неупругими |
||
и пренебрегая потерями напора. |
||
Ответ. |
pин = 0,15 МПа. |
|
386 |
|
|
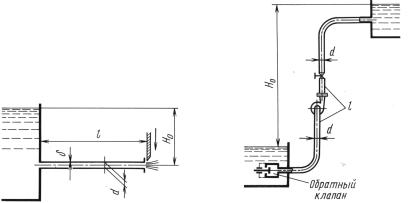
К задаче 12.20 |
|
|
|
К задаче 12.21 |
|
Задача |
12.20. Трубопровод, имеющий общую длину l = 20 м и |
||||
внутренний диаметр d = 50 |
мм и подключенный к баку с водой под |
||||
напором Н0 = 4 м, мгновенно закрывается. |
|
||||
Определить скорость а распространения ударной волны и удар- |
|||||
ное повышение давления |
pуд, если толщина стенок трубы δ = |
||||
= 6 мм и материал ее – сталь (E = 2 |
∙ |
105 МПа). Модуль упругости |
|||
воды K = 2 ∙ 103 МПа. |
|
|
|
||
Как изменится ударное давление, если стальная труба будет за- |
|||||
менена чугунной (E = 0, 9 ∙ 105 МПа) тех же размеров? Коэффици- |
|||||
ент сопротивления трения принять λ = 0,03. |
|||||
Ответ. |
Для стальной трубы а = 1365 м/с и |
pуд = 3, 5 МПа. |
|||
Задача |
12.21. Центробежный насос подает воду на высоту |
||||
H0 = 16 м по трубопроводу, имеющему общую длину l = 105 м и |
|||||
внутренний диаметр d = 75 |
мм. |
|
|
|
|
Внезапно двигатель насоса отключается от сети. Некоторое вре- |
|||||
мя столб воды в трубопроводе продолжает двигаться за счет инер- |
|||||
ции в прежнем направлении, затем скорость движения уменьшает- |
|||||
ся до нуля, после чего движение жидкости происходит в обратном |
|||||
направлении под действием напора H0. В этот момент происходит |
|||||
закрытие обратного клапана, установленного в нижнем конце тру- |
|||||
бы, и возникает гидравлический удар. |
|
||||
Определить ударное повышение давления, если обратный кла- |
|||||
пан закрылся через Т = 1 |
с после начала движения жидкости в |
||||
обратном направлении При движении жидкости через насос по следний следует рассматривать. как местное сопротивление с коэф-
-
387
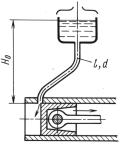
фициентом сопротивления ζ = 10 (отнесенным к скорости в тру- |
|||||||||||||||||||||
бопроводе). |
|
|
|
|
|
|
|
|
|
|
|
|
= 4, коэффициент |
||||||||
Коэффициент сопротивления задвижки ζз |
|||||||||||||||||||||
трения в трубе принять λ = 0,025. Для обратного клапана, |
проход- |
||||||||||||||||||||
ное сечение которого равно площади сечения трубы, ζк |
= 2. |
|
|||||||||||||||||||
Стенки трубы толщиной |
δ = 4 |
мм выполнены из стали (E = 2 |
× |
||||||||||||||||||
×105 МПа). |
Модуль упругости воды K = 2 ∙ 103 МПа. |
|
|
|
|||||||||||||||||
Ответ. |
|
|
pуд = 1,75 |
МПа. |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
Задача 12.22. Смазка параллелей ползуна |
||||||||||||
|
|
|
|
|
|
|
производится из масленки самотеком по труб- |
||||||||||||||
|
|
|
|
|
|
|
ке диаметром d = 6 мм и длиной l = 1 |
м через |
|||||||||||||
|
|
|
|
|
|
|
отверстие, периодически открываемое ползу- |
||||||||||||||
|
|
|
|
|
|
|
ном. |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
Считая трубку и жидкость неупругими, |
||||||||||||
|
|
|
|
|
|
|
определить количество поступающего из ма- |
||||||||||||||
|
|
|
|
|
|
|
сленки смазочного масла за один оборот ко- |
||||||||||||||
К задаче 12.22 |
ленчатого вала, |
если отверстие остается при |
|||||||||||||||||||
этом открытым в течение |
Т = 1 |
с. |
|
= 0,8 м. |
|||||||||||||||||
Кинематическая вязкость масла ν |
= 0,5 Ст. |
Напор |
H0 |
||||||||||||||||||
Течение жидкости считать ламинарным, пренебрегая кинетиче- |
|||||||||||||||||||||
ской энергией выхода из трубки. |
d2 |
|
1 , |
|
|
|
|
|
|
||||||||||||
Ответ. W = fv0 |
T + 32 |
|
e− |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
d2 |
32νT |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
||
|
πd2 |
|
|
|
|
|
|
|
ν |
|
|
|
|
|
|
|
|||||
где f = |
|
|
; v0 – скорость установившегося течения; W = 4,6 см3. |
|
|||||||||||||||||
|
|
|
|||||||||||||||||||
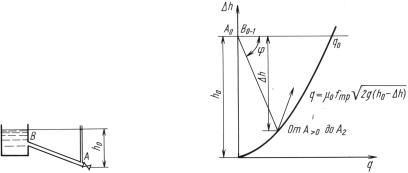
Задача |
12.23. На конце трубы мгновенно открывается кран А. |
||||||||||||||||||||
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Найти минимальное давление перед ним, если коэффициент расхо- |
|||||||||||||||||||||
да открытого крана |
μ0 |
= 0,6, скорость ударной волны а = 1 000 м/с, |
|||||||||||||||||||
статический напор перед закрытым краном h0 |
= 100 м. |
Исследо- |
|||||||||||||||||||
вать закон изменения расхода через кран. Трением в трубе пре- |
|||||||||||||||||||||
небречь. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Указание. Построив параболу расходов воды через кран по формуле |
|||||||||||||||||||||
q = μ0fтр |
|
|
|
|
|
|
и ударную характеристику трубы |
|
h(q), убе- |
||||||||||||
|
|
2g (h0 − |
h) |
|
|||||||||||||||||
ждаемся |
, что минимальное значение напора перед краном h0 |
− |
h полу- |
||||||||||||||||||
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
чается при первой фазе гидравлического удара, продолжающейся в тече- |
|||||||||||||||||||||
ние времени |
|
2l |
(см. рисунок к решению задачи). Величину |
|
h |
находим |
|||||||||||||||
|
|
|
|||||||||||||||||||
графически или аналитически из уравнения |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
а |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
388 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
К задаче 12.23 |
|
|
|
|
|
К решению задачи 12.23 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
h |
|
|
|
|
|
|
|
|
|
|
μ0fтрp2g (h0 − |
h) = |
, |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
||||||||
где tg ϕ = |
|
a |
tg ϕ |
|
|
|
|
||||||||||
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
gfтр |
|
|
|
|
|
|
|
|
|
|
h = 30 м. Расход |
||||||
Ответ. |
Минимальный напор перед краном h0 − |
||||||||||||||||
через кран стремится уменьшающимися ступенями к установившемуся |
|||||||||||||||||
значению q0 |
, каждая ступень продолжительностью а . |
|
|
|
|
||||||||||||
Задача |
12.24. В трубопроводе длиной l = |
2l |
|
|
|
|
|||||||||||
100 м и диаметром |
|||||||||||||||||
d = 100 мм, на конце которого установлен затвор, движется вода со |
|||||||||||||||||
скоростью v0 = 2 |
м/с. |
|
|
|
|
|
|
|
|
|
|
||||||
Построить график зависимости максимального ударного повы- |
|||||||||||||||||
шения напора в трубопроводе от времени полного закрытия затво- |
|||||||||||||||||
ра. Считать, что принятый закон закрытия дает линейное уменьше- |
|||||||||||||||||
ние скорости потока перед затвором по времени. Потерями напора |
|||||||||||||||||
в трубопроводе пренебречь. |
в двух вариантах: |
учитывая упругость |
|||||||||||||||
Построения выполнить |
|||||||||||||||||
системы (скорость ударной волны |
а = 1 000 м/с) и считая систему |
||||||||||||||||
неупругой. |
Сравнить ударное повышение напора, |
если время пол- |
|||||||||||||||
ного закрытия Tз |
= |
2l |
. |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
Указание. При непрямом ударе и линейном законе уменьшения ско- |
|||||||||||||||||
|
|
|
|
|
а |
|
|
|
|
|
|
|
|
Tз . |
|||
рости максимальное ударное повышение напора |
h = |
g |
|
||||||||||||||
Для неупругой системы воспользоваться выражением |
2lv0 |
1 |
инерционного |
||||||||||||||
|
|
|
|||||||||||||||
напора (12.4). |
|
|
|
|
|
|
|
|
h = 100 м. |
||||||||
Ответ. |
h = 200 м; для неупругой системы |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
389 |
||
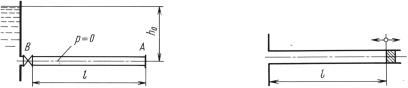
Задача 12.25. На конце трубы длиной l по направлению к ре- |
||||||||||
зервуару из неподвижного положения трогается поршень с посто- |
||||||||||
янным ускорением j. Найти максимальное и минимальное ударные |
||||||||||
давления перед поршнем и сравнить с результатом, полученным для |
||||||||||
неупругой системы жидкость |
– |
трубопровод. |
||||||||
Ответ. |
hmax |
= |
2lj |
, т. е. в |
2 |
раза больше, чем для неупругой систе- |
||||
|
||||||||||
мы; hmin = 0. |
|
g |
|
|
|
|
||||
Тупиковая труба заполнена жидкостью под атмо- |
||||||||||
Задача 12.26. |
||||||||||
сферным давлением. Кран В мгновенно открывается, сообщая тру- |
||||||||||
бу с резервуаром под постоянным напором h0. Определить ампли- |
||||||||||
туду колебаний давления у тупика в сечении А. |
||||||||||
Ответ. hmax = 2h0; hmin = 0. |
||||||||||
Задача 12.27. |
Для условий предыдущей задачи найти давление |
|||||||||
в середине трубы в момент |
3l |
(l – длина трубы, а – скорость удар- |
||||||||
|
||||||||||
ной волны). |
|
|
|
a |
|
|
|
|
||
Указание. Для решения задачи использовать двух подвижных наблю- |
||||||||||
дателей, выбывающих из сечений |
А и В навстречу друг другу так, чтобы |
|||||||||
встреча их произошла в середине трубы в момент |
3l |
. Искомый режим |
||||||||
|
||||||||||
|
|
|
|
|
|
|
|
а |
||
определяется пересечением прямых, выходящих из точек А2,5 и В2,5. |
||||||||||
Ответ. |
Напор равен h0. |
|
|
|
|
|||||
К задачам 12.26 и 12.27 |
К задаче 12.28 |
||
Задача 12.28. На конце трубы совершает гармонические колеба- |
|||
ния поршень, так что вытесняемый им расход изменяется по закону |
|||
q = qmax sin ωt, где ω – круговая частота колебаний. Показать, что |
|||
при ω = |
aπ |
, где l – длина трубы и а – |
скорость ударной волны, |
имеет место2lрезонанс, т. е. давление перед поршнем при отсутствии
трения неограниченно возрастает Смещения поршня считать ма лыми по сравнению с длиной трубы. -
Указание Воспользоваться методикой. примененной при решении примера 2 во введении. . ,
390
