
Содержание
|
1. Постановка задачи |
2 |
|
2. Вычисление матрицы коэффициентов податливости |
3 |
|
2.1. Кубическая кристаллическая решетка |
3 |
|
2.2. Гексагональная кристаллическая решетка |
3 |
|
3. Зависимость линейной податливости от направления единичного вектора |
4 |
|
3.1. Кубическая кристаллическая решетка |
4 |
|
3.2. Гексагональная кристаллическая решетка |
7 |
|
4. Оценки по Фойгту и Рейссу |
8 |
|
4.1. Кубическая кристаллическая решетка. Оценки по Фойгту |
8 |
|
4.2. Кубическая кристаллическая решетка. Оценки по Рейссу |
9 |
|
4.3. Гексагональная кристаллическая решетка. Оценки по Фойгту |
10 |
|
4.4. Гексагональная кристаллическая решетка. Оценки по Рейссу |
10 |
|
5. Задача Эшелби |
11 |
|
6. Сплав-смесь металлов |
11 |
|
6.1.
Коэффициент пористости
|
12 |
|
6.2.
Коэффициент пористости
|
14 |
|
.3.
Коэффициент пористости
|
15 |
|
7. Заключение |
17 |
|
8. Список литературы |
18 |
|
9. Приложение |
19 |
1. Постановка задачи
По значениям коэффициентов упругости кристаллов заданной пары чистых металлов вычислить элементы матрицы коэффициентов податливости и построить графики зависимостей линейной податливости от направления единичного вектора для гексагональной кристаллической решетки в плоскости, содержащей оптическую ось кристалла, а для кубической кристаллической решетки в плоскости грани и в плоскостях, содержащих имеющие общую точку диагонали двух граней, диагонали грани и куба, диагональ куба и ребро.
Для каждого из металлов в предположении хаотической ориентации зерен в поликристалле найти верхнюю и нижнюю оценки модулей сдвига, продольной и объемной упругости, а также оценки коэффициента Пуассона, и сравнить полученные значения с вычисленными для случая статистически усредненной сферической формы кристаллических зерен в поликристаллическом материале.
Провести
аналогичные расчеты и построить графики
для пористого двухфазного сплава-смеси
заданной пары металлов при трех
фиксированных значениях объемной
пористости, равных 0, 0.1 и 0.2, в зависимости
от отношения
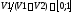 ,
где
,
где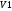 и
и - объемные доли металлов в сплаве.
- объемные доли металлов в сплаве.
|
Металл |
|
|
|
|
Литий, Li |
13,5 |
11,4 |
9,60 |
|
Металл |
|
|
|
|
|
|
Кобальт, Co |
303,5 |
161,2 |
99,8 |
354,2 |
71,9 |
2. Вычисление матрицы коэффициентов податливости
2.1. Кубическая кристаллическая решетка
Запишем матрицу жесткости для кубической решетки:

Для лития она примет вид:

где значения элементов матрицы измеряются в ГПа.
Найдем матрицу податливости, обратив матрицу жесткости:

где значения элементов матрицы измеряются в ГПа-1.
2.2. Гексагональная кристаллическая решетка
Аналогично запишем матрицу жесткости для ГПУ:

Для кобальта она примет вид

где значения элементов матрицы измеряются в ГПа.
Аналогично найдем матрицу податливости:

где значения элементов матрицы измеряются в ГПа-1.
3. Зависимость линейной податливости от направления единичного вектора
3.1. Кубическая кристаллическая решетка
Зависимость линейной податливости от направления единичного вектора в плоскости грани (рис. 1)
Воспользуемся формулой [1]
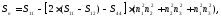 (1)
(1)
где
 -
компоненты направляющего единичного
вектора
-
компоненты направляющего единичного
вектора В нашем случае
В нашем случае
Подставим
значения компонент направляющего
вектора в формулу (1). На рис. 2 представлена
зависимость Snв ГПа от угла .
.
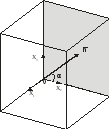
Рис.1
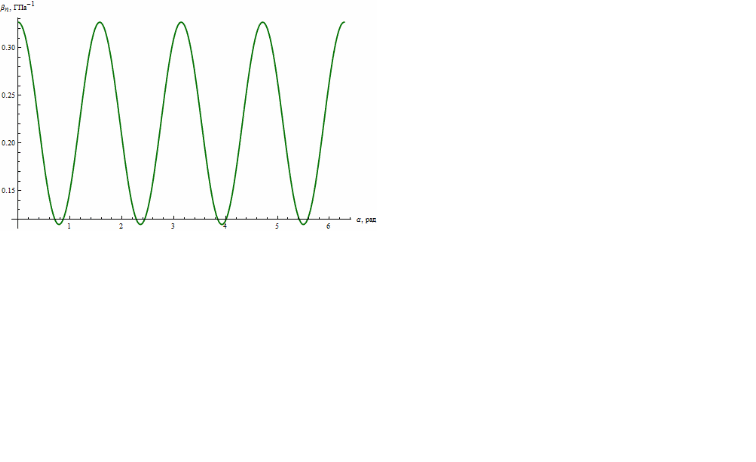
Рис.2
Зависимость линейной податливости от направления единичного вектора в плоскости, содержащей пересекающиеся диагонали двух граней (рис. 3)

Покажем,
что
 .
Уравнение плоскости, показанной на
рисунке №3, имеет вид
.
Уравнение плоскости, показанной на
рисунке №3, имеет вид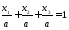 ,
где
,
где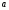 -
длина ребра куба. Пусть начало вектора,
лежащего в этой плоскости, имеет
координаты
-
длина ребра куба. Пусть начало вектора,
лежащего в этой плоскости, имеет
координаты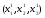 ,
а конец
,
а конец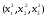 .
Начало и конец вектора принадлежат
плоскости, т.е.
.
Начало и конец вектора принадлежат
плоскости, т.е.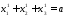 и
и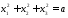 .
Вычитая второе уравнение из первого,
получим
.
Вычитая второе уравнение из первого,
получим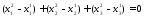 ,
или же
,
или же .
.

Рис.3
Известно,
что
 и
и .
Возведем в квадрат первое выражение,
получим
.
Возведем в квадрат первое выражение,
получим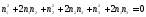 .
Или, воспользовавшись второй формулой,
.
Или, воспользовавшись второй формулой,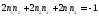 .
Возведем это выражение в квадрат, и,
вынеся одинаковые члены за скобки,
получим:
.
Возведем это выражение в квадрат, и,
вынеся одинаковые члены за скобки,
получим:
 .
.

Рис.4
Или
же
 .
Подставляя это выражение в формулу (1),
получаем
.
Подставляя это выражение в формулу (1),
получаем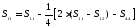 (рис 4).
(рис 4).
Зависимость линейной податливости от направления единичного вектора в плоскости, содержащей имеющие общую точку диагональ куба и ребро (рис. 5)


Рис. 5
В
этом случае
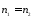 и
и ,
значит
,
значит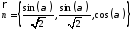
(рис. 6).
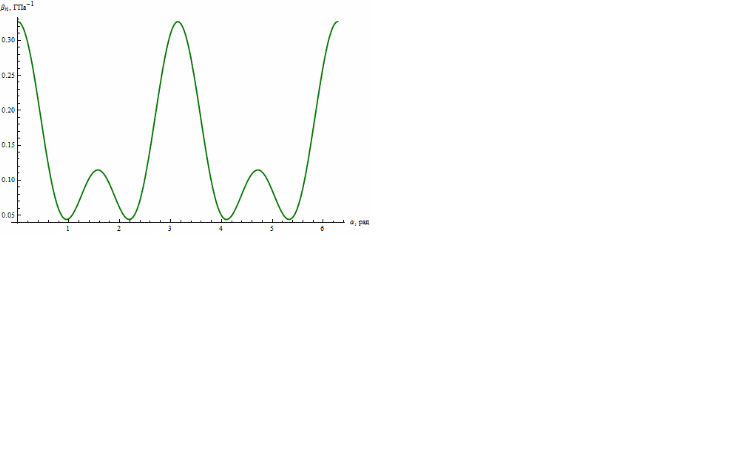
Рис. 6
3.2. Гексагональная кристаллическая решетка
Найдем зависимость линейной податливости от направления единичного вектора в плоскости, содержащей оптическую ось кристалла (рис. 7).
Для этого воспользуемся формулой [1]
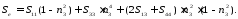

Рис. 7
Подставляя
вместо
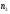 косинус угла, получаем искомый результат
(рис. 8).
косинус угла, получаем искомый результат
(рис. 8).
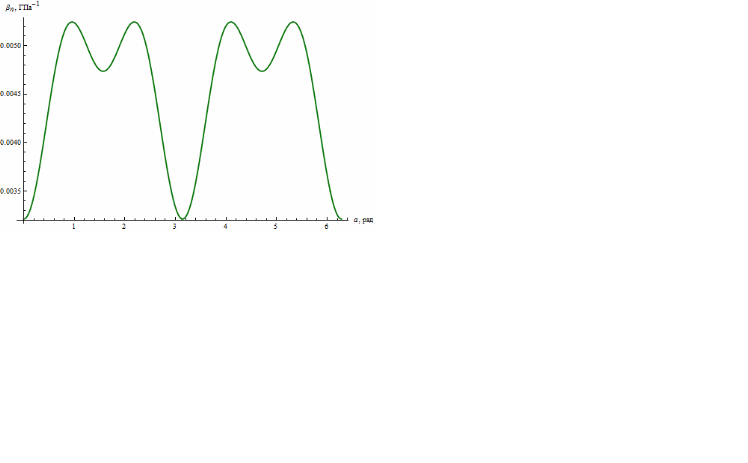
Рис. 8

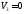
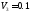

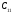 ,
ГПа
,
ГПа ,
ГПа
,
ГПа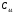 ,
ГПа
,
ГПа ,
ГПа
,
ГПа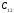 ,
ГПа
,
ГПа ,
ГПа
,
ГПа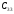 ,
ГПа
,
ГПа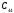 ,
ГПа
,
ГПа