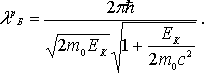2. 3. Расчет для нерелятивистских и релятивистских частиц.

Получим выражение для длины волны де Бройля частицы, обладающей кинетической энергией. Согласно(2.2)

     

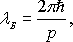
     где - импульс частицы. В случае нерелятивистской частицы, скорость которой,

     

     Поэтому

     

(2.6)

     В релятивистском случае, когда скорость частицы сравнима со скоростью света в вакууме ,, получаем, что в релятивистском случае

     

(2.7)

2. 4. Длина волны де Бройля микро- и макрообъектов.

 Для того чтобы более отчетливо представлять себе порядок величины дебройлевской длины волны микрочастиц, найдем длину волны де Бройля электрона, прошедшего ускоряющую разность потенциалов . Для определенности будем считать электрон нерелятивистским. В этом случае, согласно(2.6) ,

     

(2.8)

     Подставляя в (2.8) численные значения констант, получаем

     

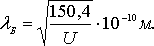
     Таким образом, при значении ускоряющей разности потенциалов в пределах от десятков вольт до нескольких киловольт дебройлевская длина волны электрона по порядку величины будет составлять м. Напомним, что эта величина имеет в физике очень большое значение: размеры атомов, а также расстояние между атомами и молекулами в твердых телах по порядку величины равным.

     Найдем теперь длину волны де Бройля у макроскопического, но достаточно малого объекта - пылинки, масса которой =г, а скорость

     = 1мм/c . Используя соотношение (2.2), получаем

     

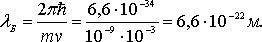
     Найденная длина волны значительно меньше не только размеров самой пылинки, но и наименьшего известного в физике размера - радиуса ядра, составляющего по порядку величины м.

     Поскольку никакого принципиального различия между микро- и макрообъектами не существует, то возникает вопрос: в каких случаях волновые свойства играют решающую роль в поведении частицы, а в каких случаях они оказываются несущественными и их можно не учитывать? Для того, чтобы ответить на этот вопрос, воспользуемся аналогией с оптикой. Как известно, волновая природа излучения максимальным образом проявляется в тех случаях, когда длина волны излучения сравнима с характерными размерами системы, т.е.. Если же, то волновые свойства излучения становятся несущественными и можно пользоваться геометрической или лучевой оптикой.

     В силу глубокой аналогии, существующей между механическими и оптическими явлениями, классическая ньютоновская механика соответствует геометрической оптике, а квантовая или, как ее еще называют, волновая механика - волновой оптике. Таким образом, волновые свойства частиц будут наиболее ярко проявляться в тех случаях, когда дебройлевская длина волны частицы сравнима с характерными размерами области движения частицы , т.е.. Напомним, что в первом из разобранных выше примеров примеров дебройлевская длина волны электрона, размеры атома и расстояние между атомами в кристалле имеют один и тот же порядок величины. Это означает, что при взаимодействии электронов с атомами, а также при их движении в твердых телах волновые свойства электронов будут проявляться максимальным образом. В тех же случаях, когда, как, например, для рассмотренной выше пылинки, волновые свойства частицы становятся несущественными, и для описания движения таких объектов необходимо пользоваться законами классической механики.