
- •5.Механика кровообращения.5.1.Давление и кровоток в артериях. Действие гравитации. Модель упругого резервуара
- •Вены с радиусом 100-50 мкм β≈0,02 гПа; Нижняя полая вена собаки β≈0,15 гПа
- •Уравнения стационарного квазиодномерного потока несжимаемой жидкости в одиночной трубке (мех-ка стационарного потока; зав-ть потока от давлений в общем виде)
- •Легочное кровообращение
- •Запирание потока в дыхательных путях при форсированном выдохе
- •4 Механика сокращения сердца.Схема анатомического строения сердца
- •Процессы, происходящие в сердце:
5.Механика кровообращения.5.1.Давление и кровоток в артериях. Действие гравитации. Модель упругого резервуара
В стенке крупн. кровен. сосудов находятся коллагеновые и эластиновые волокна. Упругость стенок определяется в основном эласт. волокнами, так как кол. волокна сориентированы т.о., что при растяжении они выпрям-ся, но не растяг-ся по направлению оси. Когда мы говорим о давл. крови, то представляем величину давл-я по отношению к атм. дав-ю, но для потока важна раз-ть давл-й вдоль сосудист. русла, а для растяж-я сосудов важно трансмуральное давление, т.е. раз-ть между давл. крови внутри сосуда и давл., действующ. на внеш. стенку сосуда. Система кровообращения(грубо):
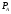 -
давление в легочной артерии,
-
давление в легочной артерии,
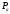 - давление в некотором артериальном
сегменте сосудистого русла,
- давление в некотором артериальном
сегменте сосудистого русла,
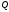 - кровоток,
- кровоток,
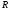 - сопротивление.
- сопротивление.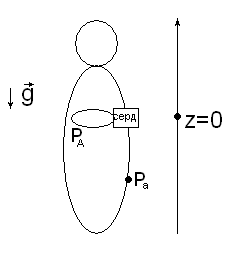
Тогда справедлива формула
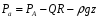
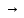 давление
крови больше внизу и меньше вверху.
Раз-ть давл-й опред. величиной
давление
крови больше внизу и меньше вверху.
Раз-ть давл-й опред. величиной
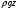 .
Такое дей-е
гравитации
может привести к явлению, назыв.
ортостатическим обмороком. if
человек резко переходит из гориз. полож-я
в вертик., давл. крови на уровне головы
резко падает, а на уровне ног – увелич..
В венах начин. накап. кровь, поэтому
возврат крови по венозной системе
уменьш. Поэтому уменьш. наполнение
сердца →, сердечный выброс. Сниж.
кровотока в аорте приводит к уменьш.
кровот. через мозговые сосуды. If
давл. крови на уровне глаз уменьш. до 30
мм.водн.ст., набл. серая пелена - на
периферии зрение ухудшается. If
давл. пад. до 10 мм.водн.ст., возник. черная
пелена – человек перестает видеть.
Сердце пыт. компенс. этот недостаток и
нач. усердно биться. В обыч. усл-х этого
мех-ма хватает для востан-я уровня
кровотока, но if
человек длительное время находился в
гориз. состоянии, то этих мех-в не
достаточно, и человек теряет сознание.
Это явление также встреч. у космонавтов,
кот. длит. t
пребывают в сост-ии антигравитации. При
перегрузках сильно возрастает g,
поэтому вертик. раз-ть давлений возраст.
пропорц. перегрузкам. Поэтому также
могут возникнуть явления черной и серой
пелены.
.
Такое дей-е
гравитации
может привести к явлению, назыв.
ортостатическим обмороком. if
человек резко переходит из гориз. полож-я
в вертик., давл. крови на уровне головы
резко падает, а на уровне ног – увелич..
В венах начин. накап. кровь, поэтому
возврат крови по венозной системе
уменьш. Поэтому уменьш. наполнение
сердца →, сердечный выброс. Сниж.
кровотока в аорте приводит к уменьш.
кровот. через мозговые сосуды. If
давл. крови на уровне глаз уменьш. до 30
мм.водн.ст., набл. серая пелена - на
периферии зрение ухудшается. If
давл. пад. до 10 мм.водн.ст., возник. черная
пелена – человек перестает видеть.
Сердце пыт. компенс. этот недостаток и
нач. усердно биться. В обыч. усл-х этого
мех-ма хватает для востан-я уровня
кровотока, но if
человек длительное время находился в
гориз. состоянии, то этих мех-в не
достаточно, и человек теряет сознание.
Это явление также встреч. у космонавтов,
кот. длит. t
пребывают в сост-ии антигравитации. При
перегрузках сильно возрастает g,
поэтому вертик. раз-ть давлений возраст.
пропорц. перегрузкам. Поэтому также
могут возникнуть явления черной и серой
пелены.
Самая
простая модель сосудистого русла –
компартментальная
модель упругого резервуара.
Эта модель рассм. с-му кровооб-я как с-му
с сосредоточ. пар-ми.В сос. русле выдел.
участки, каждый из которых явл. отдельным
упругим резервуаром. Каждый резервуар
опис. ур-ми: Q2Rab
= Pa
- Pb
; Q2-Q1
= -dVa/dt
; Pa
= (Va-Va0)/Ca,
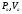 -
давл. и объем в 1м рез-ре,
-
давл. и объем в 1м рез-ре,
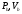 -во 2м,
-во 2м,
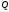 - величина кровотока,
- величина кровотока,
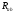 -
сопротивл. между рез-ми, С – вел-на
растяжимости рез-ра,
-
сопротивл. между рез-ми, С – вел-на
растяжимости рез-ра,
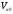 - объем 1го рез-ра, при кот. давл-я внутри
и снаружи резервуара одинаковы.
Резистивная часть между резервуарами
не облад. объемом, т.е. сколько втекло
крови, столько и вытекло. Эти уравнения
позвол. описать динамику кровообр-я в
рез-ре.
- объем 1го рез-ра, при кот. давл-я внутри
и снаружи резервуара одинаковы.
Резистивная часть между резервуарами
не облад. объемом, т.е. сколько втекло
крови, столько и вытекло. Эти уравнения
позвол. описать динамику кровообр-я в
рез-ре.


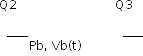
Rab
В системе кровообращения также должна быть описана насосная функция сердца.
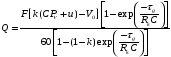 где
Q-объемный
кровоток, F
– частота сокращ-й,
где
Q-объемный
кровоток, F
– частота сокращ-й,
 -
сократит. способ-ть сердца,
-
сократит. способ-ть сердца,
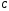 - растяжимость,
- растяжимость,
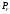 -
венозное давление на входе в сердце,
-
венозное давление на входе в сердце,
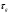 -
длительность диастолы,
-
длительность диастолы,
 -
объем нерастянутого желудочка, а величины
под экспонентой учитывают сопротивление
клапанов.
-
объем нерастянутого желудочка, а величины
под экспонентой учитывают сопротивление
клапанов.
Данная зависимость выведена на основе закона Франка-Старлинга.
5.1(Трехмерные уравнения (неразрывности и импульса – Навье-Стокса). Уравнения для линейного, невязкого варианта. Распространение пульсовой волны. Вывод формулы Моэнса-Кортевега. Нелинейные эффекты. Число Рейнольдса, число Уомерслея.
Раз с-ма имеет распределенность в пространстве, то в ней могут возникать волны. Ур-я, кот. опис. мех-ку с-мы кровооб-я, рассматриваемую как система с распределенными параметрами:
Уравнение Навье-Стокса (Уравнение баланса импульса) для несжимаемой жидкости:
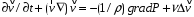 ,где
,где
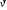 -
скорость,
-
скорость,
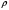 -
плотность,
-
плотность,
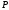 -
давление,
-
давление,
 -
коэффициент кинематической вязкости,
-
коэффициент кинематической вязкости,
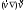 -
конвективное ускорение.Видно, что
уравнение не линейно по
-
конвективное ускорение.Видно, что
уравнение не линейно по
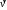 ,
поэтому решается только в простых
случаях.
,
поэтому решается только в простых
случаях.
Уравнение
неразрывности
для несжимаемой жидкости имеет простой
вид: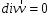
Это
2 ур-я баланса. Ур-е сохр. эн-и не нужно,
т.к. t
несжимаемой жидкости const.
Но нужно иметь замыкающее уравнение
для всей трубки в целом (закон трубки):
Эти три уравнения полностью описывают распространение пульсовой волны в сосудистом русле.
Рассмотрим
одномерный случай:1)
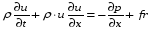 ,
где вязкостное слагаемое
,
где вязкостное слагаемое
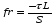 ,
что по смыслу является силой трения,
приходящ. на единицу площади сосуда.
,
что по смыслу является силой трения,
приходящ. на единицу площади сосуда.
Для течения Пуазейля τL = 8πηu, а для турбулентного потока τL = ρKtu2
2) уравнение неразрывности ∂S/∂t + ∂(uS)/ ∂x = 0
Будем
считать, что стенка невязкая,
линейно упругая.
Тогда 3) закон трубки
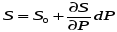
Пренебрегая
в первом уравнении вторыми слагаемыми
в левой и правой частях, получим: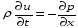 Уравнение неразрывности вместе с
законом трубки дает:
Уравнение неразрывности вместе с
законом трубки дает:
Помножив
первое из этих уравнений на
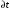 ,
а второе на
,
а второе на
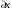 ,
получим волновое уравнение
,
получим волновое уравнение
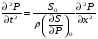 Тогда
скорость пульсовой волны равна
Тогда
скорость пульсовой волны равна
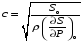 -
формула
Моэнса-Кортевега
-
формула
Моэнса-Кортевега
Для
тонкостенного сосуда, модуль упругости
которого равен
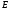 ,
а толщина равна
,
а толщина равна
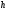 ,
а диаметр
,
а диаметр
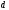
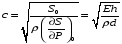
Оценим, справедливы ли наши упрощения. Мы предполож. линейность и пренебрегли конвективным ускорением. Это справедливо,if конвективное ускорение меньше, чем 1е слагаемое в уравнении Навье-Стокса. Для этого нужно, чтобы u/c << 1. Реально наблюдаются величины u/c~0.4 Второе упрощение – линеаризация кривой зависимости S от Р. Это можно делать, когда мы работаем на небольшом участке. Мы рассматривали диапазон dP/P ~ 0.2.Эти источники нелинейности искажают форму пульсовой волны, но на скорость влияют мало.Пренебрегать вязкостным слагаемым можно в том случае, если число Уомерслея (отношение сил инерции к силам вязкости) α >> 1, а в аорте человека α ≈ 20 .
Распространение
пульсовой волны
в сосудах выглядит следующим образом:←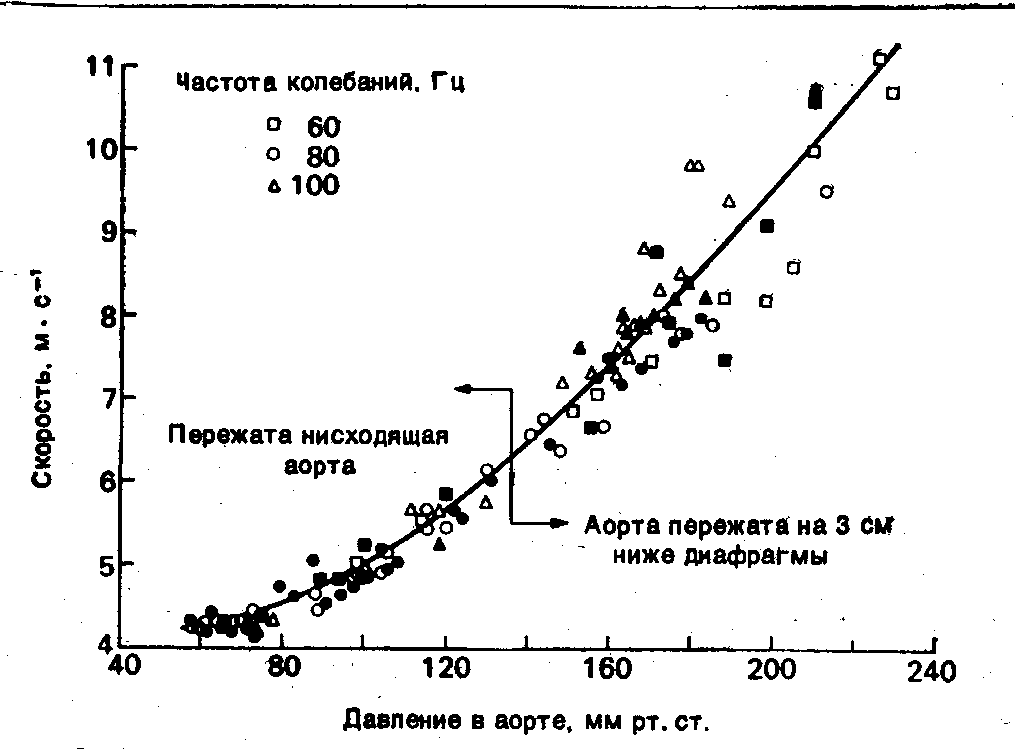
По
мере того, как давление крови повышается,
аорта растягивается и становится более
жесткой. Тогда величина
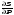 снижается, и скорость возрастает. Видно
также, что скорость пульсовой волны
мало меняется с частотой, что связано
с слабым влиянием вязкости стенки.
снижается, и скорость возрастает. Видно
также, что скорость пульсовой волны
мало меняется с частотой, что связано
с слабым влиянием вязкости стенки.
Дерево
сосудов – ветвящееся, поэтому в
бифуркациях сосудов происходит отражение
волн. Исходя из теории длинных линий,
можно найти отношение амплитуды давлений
в отраженной волне к амплитуде давлений
в падающей волне. Если у нас есть
гармонические колебания в системе, то
давление и поток связаны линейно
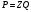 где
где
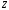 -
механический импеданс системы.
-
механический импеданс системы.
Для
трубочки сечения S
импеданс системы равен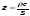 ,
где с – скорость пульсовой волны.
,
где с – скорость пульсовой волны.
Тогда
отношение амплитуд падающей и отраженной
волн (коэффициент отражения) равно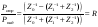 где
где
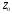 -импеданс
материнской ветви, а
-импеданс
материнской ветви, а
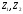 -
импедансы дочерних ветвей.
-
импедансы дочерних ветвей.
Видно,
что полное согласование возможно в
случае, когда
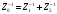
Тогда отраженная волна отсутствует. Но исследования показали, что реальная сосудистая система человека не является полностью согласованной, и в ней есть отраженные волны.
Число Рейно́льдса - безразмерная величина, характеризующая отношение нелинейного и диссипативного членов в уравнении Навье-Стокса. Число Рейнольдса также считается критерием подобия течения вязкой жидкости.
Re= ρ v L/ η= v L/ ν= Q L/ ν A где ρ — плотность среды, кг/м3; v — характерная скорость, м/с; L — характерный размер, м; η — динамическая вязкость среды, Н·с/м2; ν — кинематическая вязкость среды, м2/с ; Q — объёмная скорость потока; A — площадь сечения трубы.
5.2Кровоток в спадающихся сосудах: Механика стационарного потока в спадающихся сосудах. Запирание потока. Зависимость потока от давлений в общем виде. Спадение сосудов в легких и легочное кровообращение. Характерные параметры, скорости в венах. Метод измерения давления крови по звукам Короткова, аналогия с ударной волной в газе
Течение в спадающихся (коллапсобильных) трубках и артериях.Коллапс наблюдается в мягких податливых трубках, когда давл. снаружи трубки>давл. внутри нее. При сжатии трубки сначала сечение становится эллиптическим, а потом начинает схлопываться. Рис: зав-ть относ. изменения площади поперечного сечения от трансмурального давления в трубке:

где А0 – площадь трубки при нулевом давлении внутри нее.
Когда
давл. внутри труб. большое, труб. растянута,
имеет круглое сечение. Растяжимость
при этом мала. При уменьш. трансмур.
давл-я площадь сечения уменьшается.
Сплошная л. –для полой вены собаки,
пунктир. – для трубочки из латекса. Вена
более растяжима при больш. давл., лучше
держит форму при отриц. давл. На правом
рис. относит. изменение периметра
трубочки из латекса (треуг) и вены (крест)
в зав-ти от измен-я давл-я. При измен-и
давл-я периметр у вены мен. сильнее, чем
у лат. труб., хотя их р-ры одинаковы (внут.
d
вены и трубки 1,2 см, h/d=0,04).Cвязано
с тем, что модули Юнга различаются в 40
раз.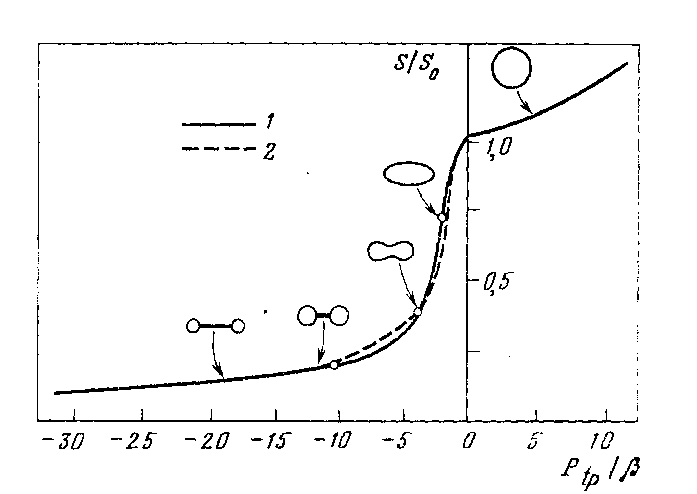
←Изменение формы сечения трубочки при измен. трансмур. давления. Форма трубочки меняется от круга до «гантельки»
При дальнейш. увелич. разницы давлений площадь открытых участков (круж.) уменьш., а длина перемычки– увел. Упругость трубочки препятствует полному схлопыванию просветов.
В
нек. диапазоне трансмур. давл-й площадь
сечения схлопывающ. трубки:(при Pтм<-β,
трубка без учета продольного натяжения)
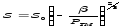 где
β – давление коллапса, т.е. давление,
при кот. трубка начинает схлопываться.
Зная геом. р-ры трубки и модуль Юнга,
можно рассчитать давление коллапса.
где
β – давление коллапса, т.е. давление,
при кот. трубка начинает схлопываться.
Зная геом. р-ры трубки и модуль Юнга,
можно рассчитать давление коллапса.
