Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Воронежский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

3484.pdf

Скачиваний:

Добавлен:

15.11.2022

Размер:

5.8 Mб

Скачать

☆

<<< < Предыдущая 1 2 34 / 54 5 > Следующая >>>

						y	.
		х2	у2 ,	tg		y		(3.5)
		х2	у2 ,	tg				(3.5)
						x
Заметим, что формула			tg	y	определяет два значения

				x
				x
полярного угла	, так как		изменяется от 0 до 2					. Из этих
двух значений	угла		выбирают то, при котором
удовлетворяются равенства (3.4).

Пример. Даны прямоугольные координаты точки: (2;2). Найти ее полярные координаты, считая, что полюс совмещен с началом прямоугольной системы координат, а полярная ось совпадает с положительной полуосью абсцисс.


Решение.	По формулам (3.5) имеем		= 2	2 , tg					1.
Согласно второму из этих равенств			или	5				.	Но

		4					4
так как x 2	0 и y 2 0 , то нужно взять					.
					4

3.3.Линии первого порядка

1.Уравнение прямой с угловым коэффициентом.

Пусть дана некоторая прямая. Назовем углом наклона

данной прямой к оси Ох угол , на который нужно повернуть ось Ох, чтобы ее положительное направление совпало с одним


из направлений прямой. Угол		может иметь различные
значения, которые отличаются друг от друга на величину			n ,
где п	натуральное число.	Чаще всего в качестве угла
наклона берут наименьшее неотрицательное значение угла			,

на который нужно повернуть (против часовой стрелки) ось Ох, чтобы ее положительное направление совпало с одним из

направлений прямой (рис. 15). В таком случае	0	< .
Тангенс угла наклона прямой к оси	Ох	называется

угловым коэффициентом этой прямой и обозначается буквой k: k tg .

Если 0 , т.е. прямая параллельна оси Ох, то k 0 .

Если 2 , т.е. прямая перпендикулярна оси Ох, то k tg

теряет смысл. В таком случае говорят, что угловой коэффициент «обращается в бесконечность».

Если известны угловой коэффициент k данной прямой и величина b отрезка 0В, который она отсекает на оси Оу (рис. 15) (т.е. данная прямая не перпендикулярна оси Ох), то уравнение рассматриваемой прямой имеет вид

y	kx b .	(3.6)
Уравнение (3.6) называют уравнением прямой с угловым
коэффициентом. Если k	0 , то прямая параллельна оси Ох,
и ее уравнение имеет вид	y	b . Итак, уравнение любой

прямой, не перпендикулярной оси Ох, имеет вид (3.6). Верно и обратное: любое уравнение вида (3.6) определяет прямую,

которая имеет угловой коэффициент			k и отсекает на оси Оу
отрезок величины b.
	Пример. Построить прямую,		заданную уравнением
у =	3	х 2 .

4

Решение. Отложим на оси Оу отрезок OВ, величина которого равна 2 (рис.16); проведем через точку В параллельно

Рис.15

Рис. 16

оси Ох отрезок,	величина которого BN	4 , и через точку N
параллельно оси	Оу отрезок, величина	которого MN 3.

Затем проведем прямую ВМ, которая и является искомой. Она

имеет угловой коэффициент k	3	и отсекает на оси Оу

	4
	4

отрезок величины b 2 .

2.Уравнение прямой, проходящей через данную точку,

сданным угловым коэффициентом. В ряде случаев возникает необходимость составить уравнение прямой, зная


одну ее точку M1(x1; y1)	и угловой коэффициент k. Запишем
уравнение прямой в виде (3.6), где b			пока неизвестное число.
Так как прямая проходит через			точку M1(x1; y1) , то
координаты этой точки		удовлетворяют уравнению		(3.6):
y1 kx1 b . Определяя	b	из этого равенства и подставляя в
уравнение (3.6), получаем искомое уравнение прямой:
y	y1	k(x x1) .		(3.7)
З а м е ч а н и е.	Если прямая проходит через точку

M1(x1; y1) перпендикулярно оси Ох, т. е. ее угловой коэффициент обращается в бесконечность, то уравнение прямой имеет вид x x1 0 . Формально это уравнение можно

получить из (3.7), если разделить уравнение (3.7) на k и затем устремить k к бесконечности.

3. Уравнение прямой, проходящей через две данные

точки. Пусть даны две точки M1(x1; y1)	и	M 2 (x2 ; y2 )
(рис. 17). Запишем уравнение прямой M1M 2	в	виде (3.7), где

k пока неизвестный угловой коэффициент. Так как прямая M1M 2 проходит через точку M 2 , то координаты этой точки

удовлетворяют	уравнению (3.7):	y2 y1	k(x2	x1) .
Определяя k	из этого равенства (при условии		x1	x2 ) и

подставляя в уравнение (3.7), получаем искомое уравнение

прямой: у у	у2	у1	(х х ) .

1	х2	1
		х1
		54

Это уравнение, если

y2 , можно записать в виде

у1

х1

(3.8)

у2

у1

х2

х1

Если y1

y2 , то уравнение искомой прямой имеет вид

y y1 . В этом случае прямая параллельна оси Ох. Если x1

x2 ,

то прямая, проходящая через точки

и M 2 , параллельна

оси Оу, и ее уравнение имеет вид

x1 .

Пример.

Составить уравнение прямой, проходящей через

точки M1 (3;1)

M 2 (5;4) .

Решение.

Подставляя

координаты точек

M1 и M 2

соотношение (3.8), получаем искомое уравнение прямой:

у 1

или

3х

2у

0 .

			Рис. 17
	4. Угол между двумя прямыми. Рассмотрим две прямые
L1 и	L2 . Пусть уравнение прямой			L1	имеет вид	у	k1х b1 ,
где k1		tg	1 , а уравнение прямой	L2	вид у	k2 х	b2 , где
k2	tg	2	(рис. 18). Пусть φ угол между прямыми L1 и
L2 :	0	φ < π.
			55

Из	геометрических			соображений						устанавливаем
зависимость между углами		1 , 2 ,					:		2	1		или
2	1 . Поэтому tg	tg(		2		1 )		tg	2	tg	1	, или
2	1 . Поэтому tg	tg(		2		1 )	1		tg	1 tg	2	, или
							1		tg	1 tg	2
	tg		k2	k1	.							(3.9)
	tg				.							(3.9)
		1		k2k1

Формула (3.9) определяет один из углов между прямыми. Второй угол равен .

				Рис 18
Пример. Две прямые заданы уравнениями											y 2x	3 и
y 3x			2 . Найти угол между этими прямыми.
Решение. Очевидно,					k1	2 ,		k2		3 ,	поэтому	по
формуле (3.9) находим
			tg		3	2			5	1.

				1	(	3) 2			5
				1	(	3) 2			5
Таким образом, один из углов между данными прямыми
равен		,	другой угол		3		.

	4			4		4

5. Условия параллельности и перпендикулярности

двух прямых. Если прямые	L1 и L2	параллельны, то	0
и tg 0 . В этом случае числитель в правой части формулы
(3.9) равен нулю: k2 k1 0,	откуда	k2 k1 . Таким образом,

условием параллельности двух прямых является равенство их угловых коэффициентов.

	Если прямые			L1 и L2	перпендикулярны, т.е.						, то
	Если прямые			L1 и L2	перпендикулярны, т.е.					2	, то
										2
		1 , tg		tg		ctg 1		1	,т.е. k2			1	.
2		1 , tg	2	tg	1	ctg 1			,т.е. k2				.
	2			2			tg	1				k1

Таким образом, условие перпендикулярности двух прямых состоит в том, что их угловые коэффициенты обратны по величине и противоположны по знаку. Это условие можно формально получить из формулы (3.9), если приравнять нулю знаменатель в правой части (3.9), что соответствует обращению

tg в бесконечность, т. е. равенству 2 .

6. Общее уравнение прямой.

Теорема. В прямоугольной системе координат любая прямая задается уравнением первой степени

Ax By Cz 0,

(3.10)

и обратно, уравнение (3.10) при произвольных коэффициентах А, В, С (А и В не равны нулю одновременно) определяет некоторую прямую в прямоугольной системе координат Оху.

Линии, определяемые в прямоугольной системе координат уравнением первой степени, называются линиями первого порядка. Таким образом, каждая прямая есть линия первого порядка и, обратно, каждая линия первого порядка

есть прямая.
Уравнение вида	Ax By C 0 называется общим

уравнением прямой. Оно содержит уравнение любой прямой при соответствующем выборе коэффициентов А, В, С.

7. Неполное уравнение первой степени. Уравнение прямой «в отрезках». Рассмотрим три частных случая,

когда

уравнение

By C

является неполным,

т.

е.

какой-то из коэффициентов равен нулю.

0 ;

уравнение

имеет

вид

определяет прямую, проходящую через начало координат.

0 (А ≠ 0); уравнение имеет вид

0 и опре-

деляет прямую, параллельную оси Оу.

Это

уравнение

приводится к виду

a , где

величина отрезка,

который отсекает прямая на оси

Ох (рис.

19). В частности,

если

0 , то прямая совпадает с осью

Оу.

Таким образом,

уравнение

0 определяет ось ординат.

(В ≠ 0); уравнение

имеет

вид

определяет прямую, параллельную оси Ох. Этот факт

устанавливается			аналогично	предыдущему случаю.		Если
положить		C	b , то уравнение принимает вид y b ,			где

		B

b	величина отрезка, который				отсекает прямая на оси Оу
(рис. 20). В частности, если b				0 , то прямая совпадает с осью
Ох. Таким образом, уравнение				y	0 определяет ось абсцисс.

Рис. 19	Рис. 20
Пусть теперь дано уравнение	Ax By C 0 при

условии, что ни один из коэффициентов А, В, С не равен

нулю. Преобразуем его к виду

	х			у	1 .

	С А			С В
	С А			С В
Вводя обозначения а =				С/А, b =		С/В, получим
		х	у	1.		(3.11)

		а b
		а b

Уравнение (3.11) называется уравнением прямой «в отрезках». Числа а и b являются величинами отрезков, которые прямая отсекает на осях координат. Эта форма уравнения прямой удобна для геометрического построения прямой.

Пример.	Прямая задана уравнением 3x 5y 15					0 .
Составить для	этой прямой		уравнение «в		отрезках»	и
построить прямю.
Решение.	Для данной прямой уравнение				«в отрезках»
имеет вид
		х	у	1.

	5		3
	5		3

Чтобы построить эту прямую, отложим на осях координат Ох и Оу отрезки, величины которых соответственно равны a 5 , b 3 , и проведем прямую через точки M1( 5;0) и

M 2 (0;3) (рис. 21).

8. Нормальное уравнение прямой. Расстояние от точки до прямой. Пусть дана некоторая прямая L. Проведем через началo координат прямую п, перпендикулярную данной, и назовем ее нормалью к прямой L. Буквой N отметим точку, в которой нормаль пересекает прямую L (рис. 22, а).

На нормали введем направление от точки О к точке N. Таким образом, нормаль станет осью. Если точки N и О совпадают, то в качестве направления нормали возьмем любое из двух возможных.

	Рис. 21
Обозначим через	угол, на который нужно повернуть

против часовой стрелки ось Ох до совмещения ее положительного направления с направлением нормали, через

рдлину отрезка ON.

Тем самым,	0	2 , p 0 . Если точки O и N
совпадают, то прямая L проходит через начало координат
(рис. 22, б) и p	0 .

Уравнение данной прямой, считая известными числа и р, имеет вид

xcos	ysin	p 0 .	(3.12)
Уравнение (3.12)	называется	нормальным уравнением

прямой L.

Рис.22 С помощью нормального уравнения прямой можно

определить расстояние от данной точки плоскости до прямой.

Пусть L

прямая, заданная нормальным уравнением

(3.12) и пусть

M 0 (x0 ; y0 )

точка, не лежащая на этой прямой.

Требуется определить расстояние d

от точки

M 0

до прямой

L. Искомое расстояние определяется формулой

x0 cos

y0 sin

(3.13)

Отметим,

что формула (3.13)

пригодна и в том случае,

когда

точка

M 0 (x0 ; y0 )

лежит

на

прямой

L, т.е. ее

координаты

удовлетворяют

уравнению

прямой

x0 cos

y0 sin

В этом случае по формуле (3.13)

получаем

d 0 .

Из

формулы (3.13) следует, что

для

вычисления расстояния d от точки

M 0

до прямой L нужно в

левую часть нормального уравнения прямой

поставить

вместо

(х,у)

координаты точки

M 0

и полученное число

взять по модулю.

Теперь покажем, как привести общее уравнение прямой к

нормальному виду. Пусть
Ax	By	C	0	(3.14)
общее уравнение некоторой прямой, а
хcos	ysin	p	0	(3.15)
ее нормальное уравнение.
		61

Так как уравнения (3.14) и (3.15) определяют одну и ту же прямую, то их коэффициенты пропорциональны. Умножая все члены уравнения (3.14) на произвольный множитель 0 ,

получаем уравнение Ах Ву С 0.

При соответствующем выборе μ полученное уравнение обращается в уравнение (3.15), т. е. выполняются равенства

А cos

sin

, C

p .

(3.16)

Чтобы найти множитель , возведем первые два из этих

равенств

квадрат

сложим,

тогда

получаем

2 (A2

B2 )

cos2

sin2

Отсюда

(3.17)

Число

называется нормирующим множителем. Знак

нормирующего множителя определяется с помощью третьего

из равенств (3.16). Согласно этому равенству	C число
отрицательное, если C 0 . Следовательно, в формуле (3.17)
берется знак, противоположный знаку С. Если C	0 , то знак

нормирующего множителя можно выбрать произвольно.

Итак, для приведения общего уравнения прямой к нормальному виду надо найти значение нормирующего множителя , а затем все члены уравнения умножить на .

Пример. Даны прямая 3x 4у + 10 = 0 и точка М(4; 3). Найти расстояние d от точки М до данной прямой.

Решение. Приведем данное уравнение к нормальному виду. Для этого найдем по формуле (3.17) нормирующий

множитель:					1			1	.
							5
				32	(	4)2
				32	(	4)2
Умножая данное уравнение на μ, получаем нормальное
уравнение	3	х	4	у	2	0 .
уравнение	5	х	5	у	2	0 .
	5		5

По формуле (3.13) находим искомое расстояние:

d			3	4		4	3	2	2	2 .

		5			5

			Задачи к п. 3
1. Даны	точки				A(0;0), B(3;				4), C( 3;4), D(		2;2) и
E(10; 3) . Определить расстояние d между точками: 1)											A и B ;
2) B и C ; 3) A и C ; 4) C и D ; 5) A и D ; 6) D и E .
2. Даны две смежные вершины квадрата A(3;7) и											B( 1;4)

. Вычислить его площадь.

3.Даны две противоположные вершины квадрата P(3;5) и Q(1; 3) . Вычислить его площадь.

4.Вычислить площадь правильного треугольника, две

вершины которого суть A( 3;2) и B(1;6) .
5.	Даны	три	вершины	A(3; 7) ,	B(5;		7)	и C(		2;5)
параллелограмма			ABCD , четвертая вершина				которого			D
противоположна B . Определить длины					диагоналей				этого
параллелограмма.
6.	Доказать,		что точки	A(3; 5) ,	B(	2;	7)	и C(18;1)
лежат на одной прямой.
7.	Даны	вершины треугольника			A(1;	3) ,		B(3;	5) и
C( 5;7) . Определить середины его сторон.
8.	Даны две смежные вершины параллелограмма A(								3;5) ,
B(1;7)	и точка пересечения его диагоналей M (1;1) . Определить
две другие вершины.
9.	Прямая проходит через точки A(7;					3) и		B(23;		6) .

Найти точку пересечения этой прямой с осью абсцисс.

10.Вычислить площадь треугольника, вершинами

которого являются точки: 1)			A(2; 3) , B(3;2)	и C(	2;5) ; 2)
M (3; 4) ,	N( 2;3) и P(4;5) .
11. Определить площадь параллелограмма, три вершины
которого суть точки A(		2;3) ,	B(4;5) и C( 3;1) .
12. Найти точку		пересечения прямых 3x		4y	29 0 и
2x 5y	19 0 .
			63

13. Даны	уравнения		двух сторон параллелограмма
8x 3y 1 0 ,	2x	y 1	0 и уравнение одной	из его
диагоналей 3x	2y 3	0 .	Определить координаты	вершин

этого параллелограмма.

14. Стороны треугольника лежат на прямых x 5y 7 0

, 3x 2y	4 0 , 7x y	19	0 . Вычислить его площадь S .
15.	Дана прямая	5x	3y 3 0 . Определить угловой

коэффициент k прямой:

1)параллельно данной прямой;

2)перпендикулярно к данной прямой.

16.	Найти проекцию точки P(	6;4)	на прямую
4x 5y	3 0 .
17. Даны вершины треугольника A(1;		1) , B(	2;1) и C(3;5) .

Составить уравнение перпендикуляра, опущенного из вершины A на медиану, проведенную из вершины B .

18. Написать уравнение сторон треугольника АВС, если задана его вершина А(1;3) и уравнения двух медиан

x	2y	1	0 и	y	1	0.
	19.		Даны	две	смежные вершины A(			3; 1)	и	B(2;2)
параллелограмма ABCD и точка Q(3;0) пересечения его
диагоналей.				Составить			уравнения	сторон		этого
параллелограмма.
	20.		Найти	точку		M1	симметричную	точке	M 2 (8;		9)
относительно прямой,						проходящей через точки A(3;				4)	и
B(	1;	2) .

21. Точка A( 4;5) является вершиной квадрата, диагональ которого лежит на прямой 7x y 8 0 . Составить уравнения сторон и второй диагонали этого квадрата.

22.Даны две противоположные вершины квадрата А(-1;3)

иС(6;2). Составить уравнение его сторон

23.Даны три вершины А(3;-4;7), B(-5;3;-2) и С(1;-2;3)

параллелограмма АВСD. Найти его четвертую вершину D, противоположную В.

24.На оси абсцисс найти точку M , расстояние которой от точки А(3;-5) равно 5.

25.На оси ординат найти точку M , равноудаленную от

точек А(1; 4;7) и В(5;6; 5).

26. Даны вершины треугольника А(3; 1;5), В(4;2; 5) и С( 4;0;3). Найти длину медианы, проведенной из вершины А.

27.	Найти	длины сторон		и	величины		углов
треугольника с		вершинами А(	1;	2;	4),	В( 4;	2;0)	и
С(3; 2;1).
28.	Заданы прямая L и точка М.			Требуется:
1)	вычислить расстояние		(М,L)		от	точки	М	до

прямой L;

2)написать уравнение прямой L проходящей через точку М перпендикулярно заданной прямой L;

3)написать уравнение прямой L, проходящей через точку М параллельно заданной прямой L.

Исходные данные:

а)	L:	2x		y	1				0,	M ( 1; 2);
б)	L: 2y 1				0,			M (1, 0);
в)	L:	x		y 1 0,					M (0;1).
В задачах 29 33 исследовать взаимное расположение
заданных прямых						L1		и L2 . Если прямые												параллельны, то
найти	расстояние								(L1, L2 ) между прямыми, а если
пересекаются				косинус угла (L ,L )										и точку M 0 пересечения
										1	2
прямых.
29.	L1 : 2x				y			1	0,	L2 : 2y				1			0.
30.	L	:	x	1		y	,			L	:		x	2			y		.
30.	L	:					,			L	:								.
	1			2	1					2	1						0
				2	1						1						0
31.	L1 : x			y	1			0,		L2 : 2x					2 y		1			0.
32.	L	: x		y	1			0,		L	:	x			y	1		.
32.	L	: x		y	1			0,		L	:							.
	1									2	2					2
33.	L1 : x			2 y	1			0,		L2 : 2x 4 y						2	0.
										65

34. Треугольник АВС задан координатами своих вершин. Требуется:

1)написать уравнение стороны (АВ);

2)написать уравнение высоты (СD) и вычислить ее

длину	h	CD	;
3)	найти угол между высотой (СD)			и медианой (ВМ);
4) написать уравнения биссектрис L1				и L2 внутреннего и
внешнего углов при вершине А.
Исходные данные: а) А(1, 2), В(2, 2), С(6, 1); б) А(2, 2),
В(6, 1), С(		2, 0).

35. Составить уравнение прямой, которая проходит через точку М(8,6) и отсекает от координатного угла треугольник с

площадью, равной 12.
		36. Написать уравнение прямой, параллельной двум
заданным прямым L1 и L2											и проходящей посередине между
ними, если:
		а) L :3x 2 y 1 0, L :											x 1						y 5			;											б)
		а) L :3x 2 y 1 0, L :																				;											б)
					1					2		2								3
												2								3
														x	1						y		1

			L : 3x 15y 1 0, L								2	:			2								2	.
															2								2

		1													5					1
															5					1
									Ответы к п. 3

1. 1)		5;			2)	10;	3)	5;	4)	5 ;		5)			2	2 ; 6)							13.				2.			137.		3.	34.

4. 8		3 .				5.	13 и 15.			7.	Середины сторон																AB ,				BC и AC
соответственно суть									(2;-4),			(-1;1),								(-2;2).							8.	(5;-3),				(1;-5).
9. (-9;0). 10. 1)								14;	2)	25.		11.				20. 12. (3; 5) .														13.		(1;	3) ,
(	2;5) ,				(5;	9) и (8; 17) . 14. S									17 . 15. 1)										5	;	2)		3		.16. (-2;-1).
(	2;5) ,				(5;	9) и (8; 17) . 14. S									17 . 15. 1)								3			;	2)	5			.16. (-2;-1).
																							3					5
17. 4x					y	3	0 .	18. x		2y		7			0,			x			4y		1				0,	x			y	2	0.
19.				3x		5y	4	0 ,			x			7y			16 0 , 3x										5y			22		0	и
x	7y				10	0 . 20. M1(10;						5) .				21.							Уравнения									сторон
квадрата:						4x	3y		1	0 ,	3x				4y					32			0 ,				4x			3y		24	0 ,
												66

3x			4y		7		0 ;						уравнение																			его							второй										диагонали:
x		7y			31		0 .							22.							3x								4y						15		0 ,							4x				3y					30 0 ,
3x			4y		10		0 ,				4x					3y			5						0 .						23.						D(9; 5;6). 13. C(6; 2),
D(2;			4).		13.				M1(7;0), M 2 (																1;0).											25. M(0;1;0).												26. 7.
27.																																																					28.
				AB	5,			BC						5 2,						AC						5;									A					,			B		C							.
				AB	5,			BC						5 2,						AC						5;									A			2					B		C				4
а)										3							x 1								y 2													2											4
				(M , L)						3		, L :					x 1								y 2								, L : 2(x 1) ( y 2) 0;
																	2								1
										5
										5
б)				(M , L)						1	, L :						x 1										y			, L : y 0;
б)				(M , L)						2	, L :						0								2					, L : y 0;
										2							0								2
в)																		x					y 1
				(M , L)							2, L :							x					y 1									, L : x y 1 0.
				(M , L)							2, L :																					, L : x y 1 0.
																	1								1
29.		Пересекаются в точке																		M											3		;		1		; cos(L L )																1	.
29.		Пересекаются в точке																		M				0									;				; cos(L L )																	.
																								0							4				2							1			2								5
																															4				2																		5
30.		Пересекаются в точке M																							(1,0);									cos(L L )											2					.
30.		Пересекаются в точке M																					0		(1,0);									cos(L L )																.
																							0														1				2				5
																																													5
31. Перпендикулярны.																	32. Параллельны, Пересекаются в точке
M			0;		1	;	cos(L L )												3			.
	0				1														3									(L , L )													2.				33.
																												(L , L )													2.				33.
					2					1				2					5												1				2
					2														5
34.			a) ( AB) :					x		1					y		2		,				(CD) :										x		6						y	1		,			h				19				,
								1									4																		4							1

																																																					17
cos					19				,			L1 :						x					1																y			2				,


					17 58												26		5						17										4		26					17
					17 58												26		5						17										4		26					17

L2 : ( 4					26		5			17)(x							1)		(					26							5				17)( y							2)			0;

б)		( AB) :			x	2		y		3	, (CD) :			x	2	y	,	h	4,		cos			1	,
				4				3						3		4
																							10
																							10
			x 2				y	2
L	:		x 2				y	2	,		L	2	: (4	2	5)(x	2)		(3		5)( y		2)	0.
L	:								,		L		: (4	2	5)(x	2)		(3		5)( y		2)	0.
1	4		2	5		3		5
	4		2	5		3		5
35.			3x	2y		12		0,			3x		8y	24	0.	36.		а)	3x		2y	7	0;
б)	x		5y	7		0.

				6
				6

4.ЛИНИИ ВТОРОГО ПОРЯДКА

Будем рассматривать линии, уравнения которых в декартовой системе координат являются алгебраическими уравнениями второй степени, то есть будем рассматривать алгебраические кривые второго порядка. Будут рассмотрены три вида линий второго порядка: эллипсы, гиперболы и параболы. Основной целью является ознакомление с важнейшими геометрическими свойствами указанных линий.

4.1.Эллипс

1.Определение эллипса и вывод его канонического уравнения.

Определение. Эллипсом называется геометрическое место точек на плоскости, для которых сумма расстояний от двух фиксированных точек плоскости, называемых фокусами, есть постоянная величина.

Для вывода уравнения эллипса выберем систему

координат xOy так, чтобы фокусы эллипса F1 и F2 лежали на оси абсцисс, а начало координат делило бы расстояние

между фокусами пополам (рис.23). Обозначим						F1F2	2c .
Тогда	координаты	фокуса	F1 будут ( c;0 ),	а	координаты
фокуса	F2 будут (	c;0) .
Возьмем произвольную точку M (x; y) , лежащую на
эллипсе. Соединим		точку	М с фокусами F1	и	F2 . Длины
			68

отрезков MF1 и MF2 обозначим соответственно через r1 и r2 : MF1 r1 ; MF2 r2 . Числа r1 и r2 называются фокальными радиусами точки М эллипса. Учитывая, что сумма r1 и r2 есть величина постоянная (это следует из определения эллипса), обозначим: r1 + r2 2a . Очевидно, что 2a 2c или a c . В

противном случае либо не существует точек, удовлетворяющих поставленным требованиям, либо совокупность этих точек сводится к отрезку F1F2 .

Рис. 23

На основании определения эллипса как геометрического места точек, можно утверждать, что для всех точек эллипса, и только для них, должно выполняться равенство:

r1 + r2

2a .

(4.1)

Определим r1

r2 по формулам расстояния между двумя

точками:

c)2

y 2 ;

(4.2)

c)2

y 2 .

(4.3)

Подставляя найденные значения r1 и

в уравнение

(4.1), получим

c)2

y 2

(x c)2 y 2

2a .

(4.4)

Уравнение (4.4) является уравнением эллипса. Однако полученная форма уравнения является неудобной для пользования, поэтому обычно уравнение эллипса дается в ином виде.

Преобразуем уравнение (4.4). Пусть M (x; y) - точка

эллипса, то есть равенство (4.4) имеет место. Перенесем первый радикал в правую часть и затем возведем обе части в квадрат

(x c)2

y 2

4a 2 4a

c)2

y 2

c)2

y 2 ,

(4.5)

или

4cx 4a 2

4a (x c)2

y 2 .

Выделим отсюда оставшийся радикал

(x c)2

y 2

a 2

cx .

(4.6)

Возведя обе части последнего равенства в квадрат, получим

a2 x2

2a2cx a2c2

a2 y 2

2a2cx

c2 x2 ,

(4.7)

откуда

(a2

c2 )x2

a2 y 2

a2 (a2

c2 ) .

(4.8)

Так

как

по

условию

c ,

то

a 2

c 2

0 .

Обозначим

разность

a 2

c2 ,

как

величину

положительную,

через

b2 a 2

c2 . Очевидно, что

a2 .

Подставляя

c2 в

равенство (4.8), получим

b2 x2

a2 y 2

a2b2

Разделив последнее равенство на

a2b2 , окончательно имеем

(4.9)

Пусть теперь х и у - любые действительные числа. Рассмотрим уравнение (4.9). По доказанному, всякая пара чисел х, у, удовлетворяющая уравнению (4.4), удовлетворяет и уравнению (4.9). Можно доказать, что и наоборот, всякая пара чисел х, у, удовлетворяющая уравнению (4.9), удовлетворяет уравнению (4.4). Произведя предыдущие выкладки в обратном порядке, мы

из равенства (4.9) получим сначала равенство (4.8), затем равенство (4.7), которое сейчас запишем в виде

a2 (x c)2

y 2

(a2

cx)2 .

Извлекая корень из обеих частей этого равенства, получим

(x c)2

y 2

(a 2

cx) .

(4.10)

Заметим теперь, что в силу равенства (4.9), должно быть

a . Так как

a и c

a , то

a . Следовательно число

a 2

cx положительно. Поэтому в правой части равенства (4.10)

необходимо взять знак плюс. Так мы приходим к равенству (4.6), после чего получим равенство (4.5); последнее мы напишем в виде

(x c)2

y 2

[2a

(x c)2

y 2 ]2 .

Отсюда

(x c)2

y 2

(2a

c)2

y 2 ) .

(4.11)

Исследуем величину

(x c)2

y 2

x2 2cx

y 2 .

(4.12)

силу равенства

(4.9) имеем x2

a2 . Далее

a2 ,

следовательно, число

2cx по абсолютному значению меньше 2a 2

. Наконец, также из равенства (4.9) заключаем, что y 2

b2 , то есть

y 2 a 2

c2 или c2

y 2

a 2 . В силу этих неравенств

вся сумма

в правой части (4.12) меньше 4a2 . Следовательно корень из этой суммы меньше 2a . Поэтому величина, стоящая внутри скобок в правой части (4.11), положительна. Отсюда вытекает, что в равенстве (4.11) перед скобками нужно брать знак плюс. Таким образом, мы получаем

(x c) y 2 2a (x c)2 y 2 ,

откуда сразу следует равенство (4.4).

Итак, уравнение (4.4) выводится из уравнения (4.9), как и уравнение (4.9) выводится из уравнения (4.4). Тем самым доказано,

что уравнение (4.9) есть уравнение данного эллипса, так как оно эквивалентно уравнению (4.4).

Уравнение (4.9) называется каноническим уравнением эллипса, это уравнение второй степени; таким образом, эллипс есть линия второго порядка.

2. Исследование формы эллипса. Приступим к изучению формы эллипса. В уравнении эллипса содержатся только члены с четными степенями текущих координат. Отсюда следует важная геометрическая особенность: эллипс, определяемый уравнением

x2	y 2	1
a2	b2

симметричен как относительно оси Ox , так и относительно оси Oy . Другими словами, если точка M 0 (x0 ; y0 ) лежит на эллипсе, то

точки M1(x0 ; y0 ) , M 2 ( x0 ; y0 ) , M 3 ( x0 ; y0 ) , симметричные точке M 0 соответственно относительно оси Ox , оси Oy и начала

О, также лежат на эллипсе. Это позволяет при изучении формы и построении эллипса ограничиться первым квадрантом, а затем получившуюся кривую с помощью зеркального отражения построить во всех четырех квадрантах. В случае канонического задания эллипса координатные оси являются осями симметрии эллипса. Точка пересечения осей симметрии называется центром эллипса.

Из канонического уравнения эллипса					x2	y 2	1 выразим	у
Из канонического уравнения эллипса					a2	b2	1 выразим	у
					a2	b2
через х:	y	b	a2	x2 .

		a
		a
Так	как	изучение		формы эллипса достаточно провести				в

первом квадранте, то в этом равенстве надо взять лишь знак плюс, то

		b
есть	y	b	a2	x2 и полагать, что x 0 .

		a
		a
	1) При		x	0 имеем y b . Следовательно, точка B1(0;b)

лежит на эллипсе.

2) При возрастании х от 0 до а у убывает.

3) При	x	a имеем		y 0 . Следовательно, точка		A1(a;0)
лежит на эллипсе.
4) При x		a получаем мнимые значения у. Следовательно,
точек эллипса, у которых			x	a , не существует.
Дадим	переменной		х	несколько	значений, 0 x	a , и,
получив соответствующие значения у,					b y 0 , построим ряд

точек, принадлежащих эллипсу. Учитывая высказанные ранее соображения и соединив найденные точки эллипса плавной линией, получим дугу эллипса B1A1 в первом квадранте. Произведя

зеркальное отображение дуги B1A1 относительно координатных

осей, получим весь эллипс. Отсюда следует, что эллипс представляет собой замкнутую кривую, с двумя взаимно перпендикулярными осями симметрии.

Рис.24

Отрезок A2 A1 и его длина 2а называются большой осью эллипса, отрезок OA1 и его длина а называются большой полуосью эллипса. Отрезок B2 B1 и его длина 2b называются малой осью эллипса; отрезок OB1 и его длина b называется малой полуосью эллипса. Длина отрезка F2 F1, то есть число 2с, называется фокусным расстоянием. Точки пересечения эллипса с

его осями A1, A2 , B1, B2 называются вершинами эллипса, а точка пересечения его осей называется центром эллипса (рис. 24).

Примечание. Если a b , то уравнение эллипса имеет вид

x2	y 2	1 или	x2 y2 a2 . Это уравнение окружности с
a2	a2

центром в начале координат и радиусом, равным а. Можно сказать, что окружность является частным случаем эллипса.

3. Эксцентриситет и фокальные радиусы эллипса.

Определение. Эксцентриситетом эллипса называется отношение фокусного расстояния к длине большой оси эллипса.

Обозначив эксцентриситет буквой

, получим:

(4.13)

Так как c

a , то

1, то есть эксцентриситет каждого эллипса

меньше единицы. Учитывая, что c2

a 2

b2 ,

получим

отсюда

2 .

Следовательно, эксцентриситет определяется отношением осей эллипса, а отношение осей, в свою очередь, определяется эксцентриситетом. Таким образом, эксцентриситет характеризует форму эллипса. Чем ближе эксцентриситет к

единице, тем меньше 1 2 , тем меньше, следовательно,

отношение ba . Т.о., чем больше эксцентриситет, тем более

эллипс вытянут. Наоборот, чем больше отношение ba , тем

меньше эксцентриситет и эллипс является менее вытянутым. В предельном случае, когда b a , то есть когда эллипс обращается в окружность, его эксцентриситет обращается в нуль.

Пусть M (x; y) - произвольная точка, лежащая на данном эллипсе. Если r1 и r2 - фокальные радиусы этой точки, то

(x c)2

y 2 ;

(x c)2 y 2

из равенства (4.6)

следует

x ;

x .

Или, так как

, то

x ; r2

x .

(4.14)

В заключение

отметим:

из

определения

эллипса

непосредственно вытекает способ построения его при помощи нити: если концы нерастяжимой нити длины 2а закрепить в

фокусах F1 и F2

и натянуть нить острием карандаша, то при

движении острия оно будет вычерчивать эллипс с фокусами F1

и F2 и суммой фокальных радиусов 2а.

Директрисы

эллипса. Построим эллипс,

заданный

каноническим уравнением

1 .

Затем построим две прямые, перпендикулярные к большой оси

эллипса,

на расстоянии

(рис. 25). Эти прямые, уравнения

которых

будут: x

и x

, называются

директрисами

эллипса. При их построении следует учесть, что

a , так как

эксцентриситет эллипса

0		x
		Рис. 25
Правая директриса, уравнение			которой x	a	, будет
Правая директриса, уравнение			которой x		, будет
проходить правее вершины эллипса			A1 , а левая	директриса,
уравнение которой x	a	, левее вершины эллипса A			(рис. 25).
уравнение которой x		, левее вершины эллипса A			(рис. 25).
			2

С помощью директрис и эксцентриситета можно выявить следующее свойство эллипса. Имеет место теорема.

Теорема. Отношение расстояния от произвольной точки M (x; y) эллипса до фокуса и до соответствующей директрисы есть величина постоянная, равная эксцентриситету кривой.

Доказательство. Пусть у эллипса F1 - правый фокус, прямая D1L1 - правая директриса, F2 - левый фокус, D2 L2 - левая директриса (рис. 25). Возьмем на эллипсе произвольную

точку M (x; y) , соединим ее отрезками MF1						и MF2 ( MF1	r1 ,
MF2	r2 ) с фокусами и опустим из нее перпендикуляры MK1						и
MK2	на обе директрисы ( MK1			d1 и MK2		d2 ) и на ось Ox .
Требуется доказать, что
		r1	r2		.
					.
		d1	d 2

На основании выведенных ранее формул имеем: r1 a x , r2 a x ,

F2 , а расстояние между

	a	x .
d1 OL1 ON	a

(Здесь N - основание перпендикуляра, опущенного из точки М на ось Ox )

x .

L2O

Вычисляя отношения

, получим:

d 2

a x (a x)

;

a x (a x)

a x

Таким образом, данная теорема доказана.

4.2.Гипербола

1.Определение гиперболы и вывод ее канонического уравнения.

Определение. Гиперболой называется геометрическое место точек на плоскости, для которых разность расстояний от двух фиксированных точек плоскости, называемых фокусами, есть величина постоянная; указанная разность берется по абсолютному значению.

Кроме того, требуется, чтобы разность была меньше расстояния между фокусами и отлична от нуля. Фокусы

гиперболы обозначим через F1 и

ними - через 2с.

Для вывода уравнения гиперболы возьмем систему

координат xOy так, чтобы фокусы гиперболы F1			и	F2	лежали
на оси		абсцисс, а начало координат делило	отрезок F1F2
	F1F2	2c пополам. Тогда координаты фокуса		F1	будут (

c;0 ), а координаты фокуса F2 будут ( c;0) (рис. 26).

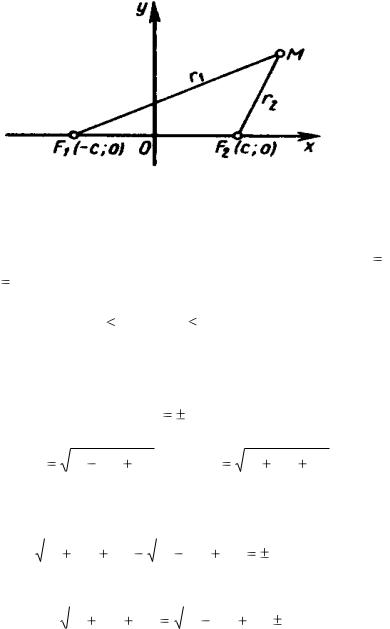
	Рис. 26
Возьмем точку	M (x; y) , лежащую	на гиперболе,		и
проведем отрезки MF1	и MF2 . Длину отрезка MF1		обозначим
через r1 , а длину отрезка MF2 - через		r2 . Т.е.	MF1	r1 ;
MF2 r2 . Числа r1 и	r2 называются фокальными радиусами

точки М гиперболы. Обозначая разность фокальных радиусов через 2а, имеем 2a 2c или a c .

На основании определения гиперболы как геометрического места точек на плоскости, можно утверждать, что для всех точек гиперболы и только для них, должно выполняться равенство

r1 - r2

2a .

(4.15)

По формуле расстояния между двумя точками имеем:

r		(x c)2	y 2 ;			r	(x c)2		y 2 .
1					2
Подставляя найденные					значения		r1 и	r2	в уравнение
(4.15), получим

	(x	c)2 y 2		(x		c)2 y 2	2a .		(4.16)
Уравнение (4.16) является уравнением гиперболы.
Приведем уравнение (4.16) к более удобному виду

		(x c)2	y 2			(x c)2	y 2	2a .

Возведем обе части в квадрат

(x c)2

y 2

(x - c)2

y 2

4a (x - c)2

y 2

4a 2

или

4cx 4a 2 4a

(x c)2

y 2 .

(4.17)

Возводя в квадрат обе части этого равенства, найдем

c2 x2

2a2cx a4

a2 x2

2a2cx a2c2

a2 y 2 ,

то есть

(c2

a2 )x2

a2 y 2

a2 (c2

a2 ) .

(4.18)

Так как по условию a

c ,

то

0 .

Обозначим

c2 a 2 b2 .

Подставив в равенство (4.18)

c2 a 2 , а

затем деля все его члены на

a 2b2 , получим

b2 x2

a2 y 2

a2b2 ,

то

1 .

(4.19)

Уравнению (4.19) будут удовлетворять координаты каждой точки, лежащей на гиперболе. Можно показать, что координаты точек, не принадлежащих гиперболе, уравнению (4.19) не удовлетворяют. Следовательно, уравнение (4.19) является уравнением рассматриваемой гиперболы. Уравнение (4.19) называется каноническим уравнением гиперболы.

2. Исследование формы гиперболы. Займемся исследованием гиперболы, определяемой уравнением

	x2		y 2	1 .
	a 2		b2

Прежде всего заметим,		что в уравнение гиперболы обе

координаты входят только в четных степенях. Следовательно,

если некоторая точка	M 0 (x0 ; y0 ) лежит на гиперболе,		то на
гиперболе будут	лежать также точки	M1(x0 ;	y0 ) ,
M 2 ( x0 ; y0 ) , M 3 (	x0 ; y0 ) ,. Отсюда следует, что гипербола

является кривой, симметричной относительно обеих координатных осей и начала координат. Это позволяет для

изучения формы гиперболы ограничиться первым квадрантом, а затем получившуюся кривую с помощью зеркального отображения построить во всех четырех квадрантах.

В случае канонического задания гиперболы координатные оси являются осями симметрии гиперболы. Таким образом, гипербола, как и эллипс, - центральная кривая.

От начала координат на оси абсцисс вправо и влево отложим отрезок, длина которого равна а, и построим точки A1(a;0) и A2 ( a;0) . На оси ординат вверх и вниз отложим

отрезок длины b и построим точки B1(0;b) и B2 (0; b) . Затем через точки A1 , A2 , B1 , B2 проведем прямые, параллельные

координатным осям, до их взаимного пересечения и таким образом построим прямоугольник (рис. 27), который назовем основным прямоугольником гиперболы.

Раствором циркуля, равным расстоянию A1B1 , из начала координат как из центра, сделаем засечки на оси абсцисс. При этом

мы найдем точки

и F2 . Действительно,

из прямоугольного

треугольника OA1B1 : OA1

a ,

OB1

b .

Следовательно, на

основании равенства

c2 ,

то получим

A B

c .

Определим

теперь

у из

канонического

уравнения

гиперболы

y 2

a 2

a2 .

Так как исследование

гиперболы

будет

вестись

в первом

квадранте, то в этом равенстве надо перед корнем взять знак плюс

	b
y	b	x2	a2	(4.20)

	a
	a

ирассматривать x 0 .

1)Если 0 x a , то у получает мнимые значения. Следовательно, точек гиперболы с абсциссами х, 0 x a не существует.

2)Если x a , то y 0 . Следовательно, точка A1(a;0)

принадлежит гиперболе.
3) Если	x a ,	то y 0 , причем при возрастании х
возрастает и у.

РРис. 27

Когда х неограниченно возрастает, у также неограниченно возрастает. Следовательно, при неограниченном возрастании х ветвь гиперболы уходит в бесконечность.

Отсюда следует, что гипербола представляет собой кривую,

состоящую из двух бесконечных ветвей (для правой ветви			r1
- r2 2a , для левой	r1 - r2	2a ) с двумя	взаимно

перпендикулярными осями симметрии, причем ни одной точки гиперболы не находится внутри основного прямоугольника.

Отрезок A2 A1 и его длина 2а называются действительной осью гиперболы, отрезок OA1 и его длина а называются действительной полуосью гиперболы. Отрезок B2 B1 и его длина 2b называются мнимой осью гиперболы; отрезок OB1 и его длина b называются мнимой полуосью гиперболы. Длина 2с отрезка F1F2 называется фокусным расстоянием. Точки пересечения гиперболы с действительной осью A1 и A2 называются вершинами

гиперболы.

3. Асимптоты гиперболы. Пусть Г - какая-нибудь линия, М - переменная точка на ней, а - некоторая прямая. Если возможно такое движение точки М по линии Г, что:

1)точка М уходит в бесконечность;

2)при этом расстояние от точки М до прямой а стремится к нулю, - то говорят, что линия Г ассимптотически приближается к прямой а. Прямая а в таком случае называется асимптотой линии Г.

Асимптотами гиперболы называются прямые, имеющие уравнения:

x и

x .

(4.21)

Эти

прямые

являются

диагоналями

основного

прямоугольника. Построим гиперболу

y 2

1 и рассмотрим

a 2

какую-нибудь

точку

M (x; y) ,

лежащую на гиперболе в первом

квадранте.

Выясним, как в первом квадранте по мере возрастания х будет изменяться расстояние от точки М гиперболы до асимптоты

x .

Обозначим

через N точку

асимптоты

абсциссой х:

N(x;Y) ,

где Y

x . Тогда

(4.22)

Так как

x , то в скобках первое слагаемое всегда больше

второго, следовательно,

y 0 , а это означает, что при одной

и той же абсциссе точка гиперболы лежит под соответствующей точкой асимптоты.

Преобразуя неравенство (4.22)

MN Y y

x2 a2

a x

a2 x

убеждаемся, что длина отрезка МN по мере возрастания х уменьшается, и когда х неограниченно растет, то MN стремится к нулю. Так как МN больше расстояния МК от точки М до асимптоты, то при этом МК и подавно стремится к нулю.

Аналогичное рассуждение можно провести в любом квадранте.


Итак, прямые y	b	x	в смысле определения являются

	a
асимптотами гиперболы	x2		y2	1 .
	a2		b2

При построении гиперболы обычно строят основной прямоугольник и проводят асимптоты, так как они позволяют точнее вычерчивать гиперболу.

4. Равнобочная гипербола. Возьмем каноническое


уравнение гиперболы	x2		y2		1 . В случае, когда	a b ,
уравнение гиперболы	a2		b2		1 . В случае, когда	a b ,
	a2		b2
уравнение гиперболы имеет вид
		x2		y2	1
		a2		a2	1
		a2		a2

или

x2 y 2 a2 .

(4.23)

Гипербола, у которой полуоси а и b равны, называется равнобочной гиперболой (рис. 28). Уравнение (4.23) называется уравнением равнобочной гиперболы. Так как основной прямоугольник этой гиперболы является квадратом, то асимптоты равнобочной гиперболы будут перпендикулярны

Рис. 28

5. Сопряженная гипербола. Рассмотрим уравнение

x2	y 2	1 .	(4.24)
a2	b2

Представим уравнение (4.24) в следующем виде

y 2	x2	1 .	(4.25)
b2	a2

Очевидно, что уравнение (4.25) представляет собой уравнение гиперболы, у которой действительной осью является ось координат, а мнимой - ось абсцисс.

Построим основной прямоугольник, проведем асимптоты и построим гиперболу (4.24). Далее в той же системе координат

построим (пунктиром) (рис. 29) гиперболу	x2	y2	1 .
построим (пунктиром) (рис. 29) гиперболу	a2	b2	1 .
	a2	b2
84

Очевидно, что гиперболы	x2	y 2	1 и	x2	y 2	1
	a 2	b2		a2	b2

имеют общие асимптоты. Такие гиперболы называются сопряженными.

Рис. 29

6. Эксцентриситет гиперболы.

Определение. Эксцентриситетом гиперболы называется отношение фокусного расстояния к длине ее действительной оси:

2c	или	c	.	(4.26)

2a		a

Так как у гиперболы c a , то эксцентриситет гиперболы больше единицы. Эксцентриситет характеризует отношение сторон основного прямоугольника, а следовательно, и форму самой гиперболы.

7. Фокальные радиусы. Из определения гиперболы (для правой ветви) следует:

		c	x a .
r	(x c)2 y 2	c
r	(x c)2 y 2
1		a
		a
	85

Так как	r	- r 2a ,	то r	c	x	a .

	1	2	2	a

Таким	образом,		получаем			формулы, выражающие

фокальные радиусы любой точки M (x; y) правой ветви через х:

r	c		x	a

1	a
				(4.27)
		c
r			x	a

2		a

Для левой ветви эти формулы примут вид

(4.28)

Выражая формулы (4.27) и (4.28) через эксцентриситет,

получим для точек правой ветви гиперболы:

(4.29)

для точек левой ветви гиперболы:

(

(4.30)

(

8. Директрисы гиперболы. Построим гиперболу,

заданную

каноническим уравнением

и две

прямые,

перпендикулярные

действительной

оси

гиперболы

симметрично расположенные относительно центра на расстоянии,

равном a (рис. 30).
Эти прямые (их уравнения x	a	и x	a ) называются

директрисами гиперболы (соответственно, правой и левой).

При их построении следует учесть, что	a	a , так как

эксцентриситет гиперболы 1 .

Рис. 30


Правая	директриса				гиперболы	x	a	будет	проходить


левее правой		вершины			гиперболы	A1 ,	а левая		директриса
гиперболы	x		a	будет проходить правее левой вершины

гиперболы A2 .

С помощью директрисы и эксцентриситета можно выявить следующее свойство, присущее гиперболе. Имеет место теорема.

Теорема. Отношение расстояний от произвольной точки M (x; y) гиперболы до фокуса и до соответствующей

директрисы есть величина постоянная, равная эксцентриситету кривой.

Доказательство. Пусть у гиперболы F1 - правый фокус, D1L1 - соответствующая ему правая директриса, F2 - левый фокус, D2 L2 - соответствующая ему левая директриса (рис. 28).

Возьмем на гиперболе произвольную точку M (x; y) , соединим ее

с фокусами MF1	r1 , MF2		r2 , затем из точки M опустим
перпендикуляры на	обе директрисы MK1 d1 и MK2 d2 .
Требуется доказать, что
		r1	r2	.
		d1	d2

Применяя выведенные ранее формулы, получим:

r1 a x , r2 a x, d1 ON OL1 x a ,

d2 ON L2O x a .

Следовательно

a x (a x)

x a

Таким образом, данная теорема доказана.

4.3.Парабола

1.Определение параболы и ее уравнение.

Определение. Параболой называется геометрическое

место точек на плоскости, каждая из которых равноудалена от данной точки, называемой фокусом, и данной прямой, называемой директрисой (предполагается, что эта прямая не проходит через фокус).

Для вывода уравнения параболы за ось Ox возьмем прямую, проходящую через фокус перпендикулярно директрисе. За положительное направление оси абсцисс возьмем направление от директрисы к фокусу.

В качестве начала координат возьмем точку О, которая делит пополам отрезок от директрисы до фокуса. Длину этого отрезка, который называется параметром параболы, обозначим

через	p . Фокус	p будет иметь координаты	p	;0 , а
			2

координаты точки оси Ox , через которую проходит

директриса, будут	p	;0
	2

Возьмем произвольную точку M (x; y) , лежащую на

параболе, соединим ее прямой с точкой F , а затем опустим из точки М на директрису перпендикуляр МК. Длина отрезка,

соединяющего точку M (x; y)

параболы с фокусом, называется

фокальным

радиусом

этой

точки

обозначается через r

(рис. 31).

Согласно определению параболы

KM .

(4.31)

Определяя FM и KM по формуле расстояния между

двумя точками, получим:

p 2

y 2

;

( y y)2 .

Следовательно,

p 2

y 2

(4.32)

Уравнению (4.32) будут удовлетворять координаты каждой точки параболы.

Рис. 31

Приведем уравнение параболы к более удобному виду, для чего возведем обе части равенства (4.32) в квадрат

		p2		p2
x2	px		y 2		px x2 .
x2	px	4	y 2	4	px x2 .
		4		4
Откуда,
		y 2	2 px .	(4.33)

Уравнение (4.33) называется каноническим уравнением параболы.

Сопоставляя равенства (4.31) и (4.32), можно выразить

фокальный радиус точки				M (x; y)			параболы через абсциссу
этой точки
			r		p	x .	(4.34)

				2
				2
2. Исследование формы параболы. Для определения
вида параболы	найдем			у		из	канонического уравнения

параболы y		2 px .
Из уравнения (4.33) следует, что х не может быть
отрицательным.	При x 0			y		0 .	Следовательно точка О(0;0)

лежит на параболе. Затем заключаем, что каждому значению x 0 соответствует два значения у, равных по абсолютной величине, но противоположных по знаку. Следовательно, парабола представляет

собой кривую, расположенную вправо от начала координат и симметричную относительно оси абсцисс.

Из формулы (4.33) следует, что по мере возрастания х возрастает и |у|, и когда х неограниченно растет, то и у по абсолютной величине неограниченно растет.

У параболы, заданной каноническим уравнением y2 2 px ,

осью симметрии является ось абсцисс. Точка пересечения параболы с осью симметрии называется вершиной параболы. В данном случае вершина параболы лежит в начале координат. Заметим, что у параболы одна вершина, у гиперболы - две, у эллипса - четыре.

Проведем на рис. 32 фокальный радиус перпендикулярно оси симметрии и определим длину LF по формуле (4.34) . Так как

абсцисса точки L равна 2p , то r p . Следовательно, число p

равняется длине фокального радиуса, перпендикулярного к оси симметрии. В связи с этим число p называют фокальным параметром параболы.

Рис. 32

Парабола, уравнение которой y2 2 px , p 0 , является кривой, расположенной справа от оси ординат (рис. 33, а).

Кривая, уравнение которой y2

2 px , p 0 , будет также

параболой. Вершина этой параболы лежит в начале координат, осью

симметрии является ось абсцисс. Все точки этой параболы лежат слева от оси ординат (рис. 33, б) .

Рис. 33 а)

Рассуждая аналогичным образом, заключаем, что уравнение

x2 2 py , p 0 , является уравнением параболы, вершина которой

лежит в начале координат, осью симметрии является ось ординат (рис. 33, в). Эта парабола лежит выше оси абсцисс. Уравнение же

вида x2 2 py , p 0 , является уравнением параболы, лежащей

ниже оси абсцисс, с вершиной в начале координат. Осью симметрии этой параболы является ось ординат (рис. 33, г).

Примечание. Условимся, наглядности ради, говорить, что

“ветви”	параболы	y2	2 px		( p	0 )	“направлены вправо”,
“ветви” параболы		x2	2 py ( p		0 ) “направлены вверх” и т. д.
Для параболы, являющейся геометрическим местом таких
точек,	которые равноудалены				от	фокуса		и директрисы	будет
справедливо равенство				r	1 ,	где	d	расстояние от	точки

				d

параболы до директрисы. Иначе, отношение расстояний от любой точки параболы до фокуса и до директрисы равно единице. По аналогии с остальными кривыми второго порядка, это постоянное отношение называют эксцентриситетом

параболы. Следовательно, эксцентриситет параболы равен единице.

б)

в)

Рис. 33 г)

Рассмотрим несколько примеров на кривые второго порядка.

Пример 1. Дано уравнение гиперболы 16х2 9 у 2 144 .

Найти длины ее осей, координаты фокусов, эксцентриситет; составить уравнение директрис и асимптот гиперболы.

Решение. Приведем уравнение гиперболы к каноническому виду и определим как параметры гиперболы, так и расстояние с от начала координат до фокуса

16х2		9 у 2		х 2		у 2
			1 или				1	,
144	144			9	16

откуда

a 3 ,

4 ,

a2 b2 5 ,

эксцентриситет

Действительная ось

6 ; мнимая ось

2b 8 .

Уравнение директрис:

Уравнение асимптот:

х .

Пример 2.

Составить уравнение эллипса, симметричного

относительно координатных осей, зная, что он проходит через

точки M1 (2;3) и M 2 1;

3 5

Решение.

Учитывая

симметричность

эллипса

относительно

осей координат,

его каноническое

уравнение

будет иметь вид:

1 и вместо текущих координат

подставим в это уравнение сначала координаты точки M1 , а

затем координаты

точки

M 2 .

Из получившейся системы

уравнений

a 2

4b2

определим параметры эллипса a и b.

Обозначив

получим следующую

систему уравнений

Решая ее, получим, что:								m			1	; n			1	,	откуда a2		16 ,
Решая ее, получим, что:								m				; n				,	откуда a2		16 ,
										16				12
b2 12 .
Следовательно, искомое уравнение эллипса будет
					х2				у 2	1.
				16				12		1.
				16				12
Пример 3. Найти вершину, фокус, ось и директрису
параболы	y	2x2	16x				29.
Решение. Преобразуем данное уравнение следующим
образом
y	2 x2	8x		29					2 x	2			8x 16 -16					29
										2
				2														2
				2														2
	2 x2	2 4x 42					3				2(x 4)2						3

							2
							2
Отсюда (x		4)2			1	( y		3) .
Отсюда (x		4)2		2		( y		3) .
				2
Обозначив		x	x	4			и		y		y		3,		перейдем к новой
системе координат O x y ,						начало которой находится в точке
O (4;3), а оси O x			и	O y			сонаправлены с осями Ox и												Oy

(рис. 34). В результате получим простейшее уравнение данной параболы

x 2 12 у.

y	y
3
3
	F
0	954

												Рис. 34
	Отсюда 2 p						1	, то есть						p		1	. Итак вершина параболы
					2								2		8

находится в точке								O (4;3); координаты фокуса xF x0												4;
yF	yO		p	3		1				23		, то		есть			F 4;	23	; уравнение	оси
		2			8			8										8

параболы		x		x0		4 , то есть							x		4		0 ; уравнение директрисы
y	y0		p	3	1				25		, то есть 8y						25	0 .
		2			8			8

4.4. Преобразование системы координат

Важной задачей аналитической геометрии является исследование общего уравнения линии второго порядка и приведение его к простейшим (каноническим) формам с помощью перехода к другим прямоугольным системам координат. При этом, естественно, изменяются как координаты точек, так и уравнения кривых. Возникает задача: как, зная координаты точки в одной системе координат, найти координаты этой же точки в другой системе координат. Решить эту задачу позволяют формулы преобразования координат.

Мы рассмотрим два вида преобразований прямоугольных координат: при параллельном сдвиге осей и при повороте осей.

1. Преобразование декартовых прямоугольных координат при параллельном сдвиге осей. При этом изменении декартовых координат меняется положение начала координат, а направление новых осей и масштаб остаются неизменными. Пусть Ox и Oy - старые, O x и O y - новые

координатные оси. Положение новых осей относительно старой системы определяется заданием старых координат нового начала: пусть O (a;b) . Произвольная точка M плоскости имеет относительно старых осей координат (x; y) , а по отношению к новым (x ; y ) . Из рис. 35 видно, что

x x a , y y b .

(4.35)

Это и есть искомые формулы. Их можно также записать в

виде

x	x	a,	y	y	b .	(4.36)
			Рис. 35

2. Преобразование декартовых прямоугольных координат при повороте осей. При этом изменении декартовых координат обе оси поварачиваются в одну сторону на один и тот же угол, а начало координат и масштаб остаются неизменными.

Пусть Ox и Oy - старые, а Ox и Oy - новые координатные оси. Положение новых осей относительно старой системы определяется заданием угла поворота новых

осей относительно старых. Обозначим этот угол буквой	.
97

Произвольная точка M плоскости имеет относительно старых осей координаты (x; y) , а по отношению к новым (x ; y ) . Из

рис.36 видно, что			x OC		OD	AB ; y CM BD AM .
Из	ODB :	OD	x cos	;	BD	x sin .
Из	MAB :	AB	y sin	;	AM	y cos .

Тогда
	x	x cos	y sin	,	y	x sin	y cos .	(4.37)
	Это и есть искомые формулы, выражающие при повороте
осей на угол			старые координаты (x; y) точки					M через
новые координаты (x ; y ) этой же точки.
					Рис. 36
	Формулы, выражающие новые координаты (x ; y ) точки
M	через	старые координаты				(x; y) , можно получить из
равенств (4.37), рассматривая их						как систему двух уравнений с
двумя неизвестными x , y , и решая эту систему относительно
x , y . Но эти формулы можно получить и сразу при помощи
следующего рассуждения: если новая система получается
поворотом старой на угол , то старая система получается
поворотом новой на угол					;	поэтому	в равенствах (4.37)
					98

можно поменять местами старые и новые координаты, заменяя одновременно на . Выполнив эти преобразования, мы получим:

x x cos

y sin ,

xsin

y cos .

(4.38)

4.5. Приведение общего уравнения линии второго порядка к каноническому виду

Общее уравнение линии второго порядка имеет следующий вид

Ax2 2Bxy Cy 2 2Dx 2Ey	F	0 ,	(4.39)
где коэффициенты A, 2B, C, 2D, 2E и	F -	любые числа и,

кроме того, числа A, B и C не равны нулю одновременно. Лемма. Пусть в прямоугольной системе координат Оху

задано уравнение (4.39) и пусть AC B2 0 . Тогда с помощью параллельного сдвига и последующего поворота oceй координат уравнение (4.39) приводится к виду

	A (x )2 C ( y )2 F		0,	(4.40)
где А', С',	F'	некоторые числа;	(х"; у")	координаты точки
в новой системе координат.
1.	Инвариантность		выражения АС – В2.
Классификация		линий второго	порядка. Коэффициенты

А, В и С при старших членах уравнения (4.39) при параллельном переносе осей координат не меняются, но они меняются при повороте осей координат. Однако выражение

AC B2 остается неизменным как при переносе, так и при повороте осей т.е. не зависит от преобразования координат.

Величина AC B2 называется инвариантом общего уравнения линии второго порядка. Она имеет важное значение в исследовании линий второго порядка. В зависимости от знака

величины AC B2 линии второго порядка разделяются на следующие три типа:

1)	эллиптический, если AC B2	0 ;
2)	гиперболический, если AC B2	0 ;
3)	параболический, если AC B2	0 .
Рассмотрим линии различных типов.
1)	Э л л и п т и ч е с к и й	т и п. Поскольку

AC B2 0 , то coгласно лемме, общее уравнение линии второго порядка может быть приведено к виду (для удобства записи опускаем штрихи у коэффициентов и координат)

		Ax2 Cy 2				F	0 .
Возможны следующие случаи:
а)	A	0 , C 0 (случай		A		0 ,	C 0 сводится к случаю
A 0 ,	C	0 умножением уравнения на – 1) и F 0 . Перене-
сем F в правую часть уравнения и разделим на него. Уравнение
принимает вид
			x2	y	2	1 ,
			a2	b2		1 ,
			a2	b2

где a2 FA , b2 CF . Сравнивая полученное уравнение с

уравнением эллипса, заключаем, что оно является каноническим уравнением эллипса.

б) A 0 , C 0 и F 0 . Тогда, аналогично предыдущему, уравнение можно привести к виду

x2	y 2	1.
a2	b2

Этому уравнению не удовлетворяют координаты никакой точки плоскости. Оно называется уравнением мнимого эллипса.

в) A 0 , C 0 и F 0 . Уравнение имеет вид ( a2 A, c2 C )

a2 x2 c2 y2 0 .

100

Ему удовлетворяют координаты только одной точки x 0

, y

0 .

Такое уравнение назовем уравнением пары мнимых

пересекающихся прямых.

Г и п е р б о л и ч е с к и й

т и п.

Поскольку

0 , то согласно лемме общее уравнение линии

второго порядка приводится к виду

Ax2 Cy 2

0 .

Возможны следующие случаи:

а)

0 ,

0 (случай A

0 ,

0 сводится к случаю

0 , C

0 умножением уравнения на

–1) и F

0. Пусть,

например, F

0 . Перенесем

в правую часть уравнения и

разделим на него. Уравнение принимает вид

где

. Сравнивая с уравнением гиперболы,

заключаем, что полученное уравнение является каноническим уравнением гиперболы.

б)

0 , C

F 0 . Уравнение принимает вид (

A, c2

C )

a2 x2

c2 y2

или

(ах - су) (ax + су) = 0.

Последнему

уравнению

удовлетворяют

только

координаты

точек

плоскости, расположенных

на прямых

0 , пересекающихся в начале координат,

и, таким образом, имеем пару пересекающихся прямых.

3) П а р а б о л и ч е с к и й

т и п. Если

0 , то

поворотом осей координат на угол ,

общее уравнение линии

второго порядка может быть приведено к виду

Ax2

Cy 2

2Dx 2Ey F 0 .

(4.41)

Здесь

и,

следовательно, один из коэффициентов

или

равен нулю. Пусть

0 ,

С 0.

Представим

уравнение (4.41) в виде

101

С y 2

2Dx

E 2

0 ,

или

C y

2Dx

0 ,

где

F *

E 2

Перенесем начало координат параллельно

оси

Оу

в точку

, т.е. перейдем к новым координатам

по

формулам

x ,

Получим

уравнение

C( y )2

2Dx

0. Возможны следующие случаи:

а)

0 .

Запишем

уравнение

виде

C( y )2

2D x

F *

Перенесем теперь начало координат

F *

параллельно оси

Ох'

в точку

;0 ,

т.е. перейдем к

F *

новым координатам по формулам

, y

y .

Получим уравнение

C( y )2

2Dx

или

( y )2

2 px ,

где

Сравнивая последнее уравнение с уравнением

параболы, заключаем, что оно является каноническим уравнением параболы.

б)	D	0 . Уравнение имеет вид	C( y )2 F	0. Если
С и	F *	имеют разные знаки, то,	полагая	F *	a 2	,
				F *
				C
				C
		102
		102

уравнение можно записать в виде (y - a)(y + a) = 0. Это уравнение определяет пару параллельных прямых.

Если С и F * имеют одинаковые знаки, то уравнение

принимает вид ( y )2 a2 0. Этому уравнению не

удовлетворяют координаты никакой точки плоскости. Оно называется уравнением пары мнимых параллельных прямых.

Наконец, если F *	0 ,	то уравнение принимает вид
( y )2 0 и определяет	ось	О'х'. Это	уравнение	можно
рассматривать как предельный случай при			F * 0 , т.	е. как
уравнение пары совпавших прямых.
Заканчивая исследование		общего	уравнения	линии

второго рядка, сформулируем полученные результаты в виде теоремы.

Теорема. Пусть в прямоугольной системе координат

задано	общее	уравнение	линии	второго	порядка
Ax2 2Bxy Cy 2		2Dx 2Ey F	0 .	Тогда существует

такая прямоугольная система координат, в которой это

уравнение

принимает

один

из

следующих

девяти

канонических видов: 1)

y 2

= 1 (эллипс); 2)

y 2

(мнимый

эллипс);

a2 x2

c2 y2

0 (пара

мнимых

y 2

пересекающихся

прямых);

= 1 (гипербола);

5)a2 x2

6)y2 2 px

прямых);

прямых); 9)

c2 y2	0	(пара		пересекающихся		прямых);
(парабола);			7)	y2 a2	0 (пара параллельных
8)	y2	a2	0	(пара	мнимых	параллельных
y2	0 (пара совпавших прямых).

103

2. Приведение к каноническому виду общего уравнения центральной линии второго порядка. Пусть дано общее уравнение кривой второго порядка

Ax2 2Bxy Cy 2 2Dx 2Ey F 0 .

(4.39)

Попытаемся упростить это уравнение путем перехода к другим координатам. В результате преобразования нужно добиться:

1)Чтобы в группе старших членов исчез член с произведением текущих координат.

2)Чтобы число членов первой степени стало наименьшим, а если возможно – совсем их уничтожить.

3)Если возможно уничтожить свободный член.

В результате мы получим уравнение кривой второго порядка, называемое каноническим.

а) Прежде всего попытаемся упростить уравнение (4.39) путем параллельного переноса координатных осей. Перенесем начало координат в точку S (x0 ; y0 ) , которую пока будем

считать произвольной. Из формул преобразования при параллельном переносе следует

x0 ,

y0 ,

(4.42)

y y

где

новые

координаты

произвольной

точки.

Подставляя (4.42) в (4.39), получим

A(x x0 )

2B(x x0 )( y y0 ) C( y y0 )

2D(x x0 )

y0 )

~ 2

2( Ax0

By0

(4.43)

2E( y

2Bxy

D)x

2(Bx0

Cy0

E) y

Ax02

2Bx0 y0

Cy02

2Dx0

2Ey0

где

F .

преобразованном уравнении (4.43) члены

первой

степени

исчезнут,

если

подобрать

так,

чтобы

удовлетворялись уравнения

104

Ax0

By0

Bx0

Cy0

0 .

(4.44)

Обозначим буквой

определитель системы (4.44)

Этот определитель составлен из коэффициентов при

старших

членах

уравнения

(4.39)

называется

дискриминантом старших членов этого уравнения. Если

0 ,

то система (4.44) совместна и

имеет единственное решение

(x0 ; y0 ) . С учетом (4.44) уравнение (4.43) примет вид

(4.45)

2Bxy

где свободный член

F с учетом (4.44) можно преобразовать

Cy02

F ( Ax0

F Ax02

2Bx0 y0

2Dx0

2Ey0

By0

D)x0

(Bx0 Cy0

E) y0

Dx0

Ey0

F Dx0

Ey0

или

Dx0

Ey0

F .

(4.46)

Вернемся к

уравнению

(4.45). При

замене

~ ~

на

(x; y)

его левая часть не меняется.

Это значит,

что если

( x;

точка

~ ~

на кривой,

определяемой

уравнением

M (x; y) лежит

(4.45), то и симметричная ей точка

M (

также лежит на

этой кривой. Но точки

M и

симметричны относительно

точки

S (x0 ; y0 ) .

Поэтому точка

в этом случае называется

центром симметрии или просто центром данной кривой. Теперь становится очевидным геометрический смысл преобразования, при котором исчезают члены первой степени: начало координат переносится в центр кривой.

Определение. Кривая второго порядка, имеющая единственный центр, называется центральной. Признаком

центральной кривой служит неравенство	0 .
б) Продолжим упрощение уравнения (4.45). Попытаемся
уничтожить член, содержащий произведение		~~	путем
уничтожить член, содержащий произведение		xy	путем
105

поворота перенесенных осей на некоторый угол											. Из формул
преобразования координат при повороте осей следует
			~		x cos		y sin		,		(4.47)
			x		x cos		y sin		,		(4.47)
			~		x sin			y cos .
			y		x sin			y cos .
Подставляя			(4.47)			в	уравнение (4.45)				и приводя
подобные, получим
A(x cos	y sin	)2		2B(x cos				y sin	)(x sin		y cos )
C(x sin	y cos		)2		~
C(x sin	y cos		)2	F
( A cos2	2B cos		sin			C sin2		)x 2			(4.48)
2( A cos	sin	B cos2				B sin2		C cos		sin	)x y
( Asin2	2B cos		sin			C cos2		) y 2	~	0
( Asin2	2B cos		sin			C cos2		) y 2	F	0

В уравнении (4.48) члены с произведением x y

исчезнут, если угол поворота выбрать так, чтобы коэффициент при x y обратился в нуль

Acos sin	B cos2	B sin2	C cos	sin 0 ,
или
Bsin2	(A C) cos sin		B cos2	0.
После деления на cos2 , получим
Btg 2	(A C)tg	B	0 .	(4.49)

Уравнение (4.49) является квадратным уравнением

относительно tg .

Решив его,

в общем случае мы найдем два

корня: (tg )1

и (tg

)2 . Однако в формулах для поворота (4.47)

фигурируют

sin

и cos .

Зная tg ,

их легко найти по

формулам тригонометрии

sin

;

cos

(4.50)

tg 2

Знак выбирается в зависимости от того, в какой четверти находится угол, определяемый соответствующим tg .

106

В системе координат, повернутой на угол		, опреляемый
по (4.50), уравнение (4.48) примет вид
A x 2 C y 2	~	(4.51)
	F 0 ,
где A и C - постоянные коэффициенты при		x 2 и y 2 в

уравнении (4.48). Уравнение (4.51) представляет собой канонический вид общего уравнения центральной линии второго порядка.

Пример 1. Привести к каноническому виду уравнение
	x2 6xy y2	4x 4y 12 0 .	(а)
Решение.	Здесь	A 1, B 3, C 1, D	2,
E 2, F 12.	Прежде чем использовать изложенную схему,

нужно убедиться, что данное уравнение представляет центральную линию второго порядка. Составим определитель

1	3	8 0 .	Следовательно,	данная	линия
3	1

центральная и для освобождения в ее уравнении от членов первого порядка перенесем начало координат в центр этой линии. Его координаты удовлетворяют уравнениям

x0	3y0		2 0	x0	3y0	2 0			y0		1,
3x0		y0	2 0		8y0	8 0			x0		1.
	Центр линии располагается в точке S(							1;	1) . Подсчитаем,
чему будет равен свободный член						~	после переноса начала
чему будет равен свободный член						F	после переноса начала
координат			в т. S :	F	2 (	1)	2 (	1)	12	16 .	Само
уравнение после применения параллельного сдвига										x	~
уравнение после применения параллельного сдвига										x	x 1,
y	~	1 примет вид
y	y	1 примет вид
			~2	~~	~2	16	0 .				(б)
			x	6xy	y	16	0 .				(б)

Для освобождения от члена, содержащего произведение

xy , применим преобразование поворота осей на некоторый

угол

107

													~		x cos							y sin							,
													x		x cos							y sin							,
													~		x sin									y cos .
													y		x sin									y cos .
		Для				определения								конкретного												значения				угла				имеем
уравнение
							3tg 2						0 tg						3		0				или				tg 2	1 .
		Отсюда									(tg		)1 1								и							(tg )2		1 .			Выберем
положительное значение																tg					1, что соответствует острому
углу поворота									осей										.			Тогда							sin			1			1		;
																4																					;
																														1			1		2
																														1			1		2
cos					1			1				. Формулы поворота в этом случае имеют

					1	1		2
					1	1		2
вид
								~			1					1									1				y ) ,
										x				x						y								(x

													2			2									2
													2			2									2
								~			1					1									1			(x y ) .								(в)
										y				x						y

													2			2									2
													2			2									2
Подставляя (в) в (б), получим
			1	(x y )2							3(x y )(x y )														1		(x y )2			16 0 .
2				(x y )2							3(x y )(x y )														2		(x y )2			16 0 .
2																									2
Раскрывая скобки и приводя подобные, имеем
	1	x 2			x y			1		y 2			3x 2				3y 2						1		x 2				x y	1	y 2		16 0 ,
2		x 2			x y			2		y 2			3x 2				3y 2				2				x 2				x y	2	y 2		16 0 ,
2								2													2									2
			x 2			3x 2 3y 2								y 2		16 0 ,												2x 2 4y 2					16 .
															x 2			y 2
Делим на (-16), тогда																						1.
Делим на (-16), тогда														8					4			1.
														8					4
			Получено									каноническое												уравнение						гиперболы							с

действительной полуосью a 8 , мнимой b 2 . Выполним последовательное построение этой гиперболы (рис. 37).

108

Рис. 37

Замечание. Из сопоставления с классификацией линий второго порядка получаем, что уравнение центральной линии может быть только эллиптического или гиперболического типа

( 0) .

3. Приведение к каноническому виду общего уравнения кривой второго порядка параболического типа.

Для уравнения параболического типа 0 . Схема приведения к каноническому виду уравнения центральной линии здесь не годится. Упрощение параболического уравнения целесообразно начать с поворота координатных осей на угол при помощи формул

~	x cos	y sin ,
x
~	x sin	y cos .
y
	109

Угол поворота определится из уравнения

Btg 2 (A C)tg B 0 .

В преобразованном уравнении исчезнет член с произведением x y. Дальнейшее упрощение преобразованных уравнений достигается путем параллельного переноса уже повернутых осей.

Пример 2. Привести к каноническому виду уравнение

4x2	4xy y2	2x 14y 7 0 .				(а)
Решение.	Здесь	A 4,		B 2,		C 1, D 1,
E 7, F 7 . Вычислим				2	0 .	Данная линия
			4	2
			2	1
			2	1

принадлежит к параболическому типу. Для освобождения от члена, содержащего произведение координат, повернем оси на

угол				,			определяемый										из				уравнения
Btg 2	(A		C)tg				B		0 .			В				нашем					случае
2tg 2		3tg		2		0 или						2tg 2	3tg				2 0 .			Его решения
(tg )	2	и		(tg	)					1	. Возьмем первое значение tg											2 .
(tg )	2	и		(tg	)	2					. Возьмем первое значение tg											2 .
1						2			2
									2
В										этом											случае
sin		tg				2		;				cos		1					1		.
								;				cos									.
	1	tg		2		5							1		tg	2	5
				2		5										2	5

Преобразование координат будет иметь вид
				x	x cos							y sin	1		(x		2y ) ,

													5
													5
				y	x sin						y cos		1		(2x			y ) .				(б)

													5
													5

Подставляя (б) в (а), получим

110

4		(x			2 y )2				4	(x				2 y )(2x					y )			1		(2x			y )2						2		(x				2 y )
		(x			2 y )2					(x				2 y )(2x					y )					(2x			y )2								(x				2 y )
5					5																	5											5
	14			(2x y ) 7										4	x 2			16	x y				16		y 2			8	x 2					16		x y				4	x y
				(2x y ) 7											x 2				x y						y 2				x 2							x y					x y
	5													5			5					5					5						5						5
		8	y 2			4		x 2			4	x y				1	y 2			2	x					4	y				28	x				14		y 7 0.
	5				5					5					5												y					x						y 7 0.
																			5					5					5						5
																			5					5					5						5
5y 2					30					10							0,		или				5y 2																7 0 .
					30		x			10			y		7												6			5x			2				5y

					5					5
					5					5

Данное уравнение не содержит члена с произведением x y. Дальнейшее упрощение производится с помощью параллельного переноса координатных осей. Для этого выделим полный квадрат по переменной y

			5 y 2				5			1	1
				2 y			5			1	1				6 5x 7						0 или

					5					5	5
					5					5	5
										2
					5					2
		5		y	5						1		6			5x		7			0 .

					5
					5
	Приводя подобные, получим
		2																2
	5	2												5				2				1
5 y	5		6 6 5x 0							;		5 y		5							6 5 x	1	0 ;

	5													5
																						5
																						5
								2
			y			5		2		6 5				x				5			0 .
			y		5						5			x				5			0 .
					5						5							5
Введем новые координаты										~	и		~
Введем новые координаты										x	и		y :

					~					5				~				5
				y		y						,	x				x			.
				y		y				5		,	x				x		5	.
Тогда последнее уравнение примет вид

					~ 2						6		5 ~
									y						x .
									y				5		x .
													5
											111

А это - каноническое уравнение параболы с параметром

3 5

с вершиной

т.

~ ~~

O(0;0)

системе xOy .

Выполним

последовательное

построение

этой

параболы

(рис. 38).

Рис. 38

Пример 3. Привести к каноническому виду уравнение

8x2

4xy 5y2

16x 4y 28 0 .

Решение.

Здесь

5, D

2, F

28. Вычислим

0 .

Данная линия

принадлежит к эллиптическому типу. Прежде всего

освободимся от членов с первой степенью переменных, для

чего начало координат перенесем в центр данной линии. Его

координаты найдем из системы:

8x0	2 y0	8 0	18y0	0	y0	0,
2x0	5y0	2 0 ( 4)	2x0 5y0	2 0	x0	1.
			112

Преобразование параллельного переноса будет иметь вид:

	x		~	a	~	1,								y	~							~						В			этом			случае
	x		x	a	x	1,								y	y b							y .						В			этом			случае
~			Dx0		Ey0			F		8			0		28				36 .								В		системе						~		~~
	F		Dx0		Ey0			F		8			0		28				36 .								В		системе						xOy
																						~2					~~		~2			36			0 (*).
уравнение линии приобретает вид 8x																											4xy		5y			36			0 (*).
			Для освобождения от члена с																								произведением								~~
			Для освобождения от члена с																								произведением									xy ,
проведем поворот координатных осей на угол																														.		Его найдем
из уравнения							2tg 2				3tg				2				0 . Его решение												(tg		)		1			и


																																	1		2
																																			2
(tg			)2		2 .	Возьмем,								например,									первое					значение					tg					1	.
(tg			)2		2 .	Возьмем,								например,									первое					значение					tg				2		.
																																					2
Тогда								sin					1 2						1					;			cos					1					2			.

													1		1 4				5											1		1 4					5
													1		1 4				5											1		1 4					5
Преобразование поворота будет иметь вид
								~	2						1							1						y ) ,
								x				x						y								(2x

									5						5							5
									5						5							5
								~	1						2							1						2 y ) .
								y				x						y								(x

									5						5							5
									5						5							5
					~			~	в уравнение (*), получим
Подставляя x							и y		в уравнение (*), получим
	8	(2x		y )2			4	(2x		y )(x 2 y )											5				(x 2 y )2					36 0;
5		(2x		y )2		5		(2x		y )(x 2 y )									5						(x 2 y )2					36 0;
5						5													5
32x 2				32x y 8y 2						8x 2					4x y 16x y 8y 2															5x 2			20x y
		20y 2			180	0;
45x 2				20y 2				180	0 ;							x 2				y 2							1 .
45x 2				20y 2				180	0 ;								4					9					1 .
																	4					9

Получили каноническое уравнение эллипса. Выполним последовательное построение этого эллипса (рис. 39).

113

					Рис. 39
	Пример 4. Привести к каноническому виду уравнение
		3x2		10xy 3y2		16x	16y	16		0 .
	Решение.		Здесь A		3, B	5, C	3, D		8,	E	2, F	16 .
Вычислим			3	5	16	0 . Уравнение гиперболического
Вычислим			5	3	16	0 . Уравнение гиперболического
			5	3
типа.
3x0	5y0	8 0 ( 5)				10y0		16 0			y0	1,
5x0	3y0	2	0	(3)		5x0	3y0	8	0		x0	1.
					114

1 .

этом

случае

(

0 .

В системе

уравнение линии

F 8 (

xOy

преобретает вид

0 .

Для освобождения от

10xy

члена с произведением

xy , проведем поворот координатных

осей на угол . Его найдем из уравнения

5tg 2

0 . Его

решение

(tg

1 . Возьмем, например,

первое значение

Тогда

sin

;

cos

Преобразование поворота будет иметь вид

(x y ) ,

(x y ) .

y )2

y )(x

y )

y )2

3x 2

6x y 3y 2

10x 2

10y 2

3x 2

6x y 3y 2

16x 2

4y 2

0 ;

y 2

4x 2 ; y 2x и y

2x .

Получена пара пересекающихся прямых (вырожденная гипербола рис. 40).

115

Рис. 40

Задачи к п. 4

1.Установить, что каждое из следующих уравнений

определяет окружность, найти ее центр С и радиус R:

а)	x2	y2	4x 6y 3 0;	б) x2 y2 8x 0,	в)
x2	y2	4y	0.

2.Написать уравнение окружности в каждом из

следующих случаев (обозначено: С					центр окружности,			R
радиус,	M , M1, M 2 , M 3		точки на окружности): а)				C(2;	3) ,
R 7 ;	б)	M (2;6) , C( 1;2);		в) М1(3; 2) , М 2 (		1;6)	концы
диаметра		окружности;	г) С(1; 1),		прямая 5x	12y	9	0
касательная к окружности.
3. Построить эллипс 9x2				25y2	225. Найти: а) полуоси,
б) координаты фокусов,			в)	эксцентриситет,		г) уравнения
директрис.
			116

4. Написать каноническое уравнение эллипса, если:

а) а = 3, b = 2;			б) a = 5, c = 4;	в) с = 3,	3	; г) b = 5,
					5
12	;	д) c = 2	и расстояние между директрисами равно 5;
13
е)	1	и расстояние между директрисами равно 32.
е)	2	и расстояние между директрисами равно 32.
	2
5.		Установить, что каждое		из следующих		уравнений

определяет эллипс, найти его центр С, полуоси, эксцентриситет и уравнения директрис:


a)	5x2	9y2	30x 18y 9 0;
б) 16x2		25y2		32x 100y		284 0;
в) 4x2		3y2	8x 12y 32			0.
6.	На эллипсе 9x2				25y2	225	найти точку, расстояние
от которой до фокуса				F2	в четыре раза больше расстояния до

фокуса F1 .

7.Написать уравнение кривой, по которой движется

точка	М,	если сумма расстояний	от нее до		точек

F1( 1;	1)	и F2 (1;1) остается постоянной и равной 2		3.

8. Написать уравнение кривой, по которой движется точка М, если расстояние от нее до точки F(3;0) остается в два раза меньше расстояния до прямой x y 1 0.

9. Определить, как расположена прямая относительно эллипса: пересекает, касается или проходит вне его, если прямая и эллипс заданы уравнениями:

					x2			y2
а)	2x	y	3	0,							1,
а)	2x	y	3	0,	16				9		1,
					16				9
						x2				y2
б)	2x	y	10	0,									1,
б)	2x	y	10	0,	9				4				1,
					9				4
							x2					y 2
в)	3x	2 y	20 0,											1.
в)	3x	2 y	20 0,				40		10					1.
							40		10
									117

10.

Построить гиперболу

16x2

9y2

144.

Найти:

а)

полуоси;

б) координаты фокусов;

в) эксцентриситет;

г) уравнения асимптот; д) уравнения директрис.

11.

Написать каноническое уравнение гиперболы, если: а)

а = 2, b = 3; б) b = 4, c = 5; в) с = 3,

; г) а = 8,

;

д)

с =

и уравнения асимптот

x ;

е)

расстояния между директрисами равно 83 .

12. Установить, что каждое из следующих уравнений определяет гиперболу, найти ее центр, полуоси, эксцентриситет, уравнения асимптот и директрис:

а) 16x2	9y2	64x 54y 161		0;
б) 16x2	9y2	64x 18y 199		0;
в) 9x2	16y2	90x 32y 367		0.
13. Найти точки гиперболы			x2		y	2	1,	находящиеся на
13. Найти точки гиперболы			9	16			1,	находящиеся на
			9	16

расстоянии 7 от фокуса	F1 .
14. Построить следующие параболы и найти их
параметры:
а) у2 6x , б) x2	5y, в) y2	4x, г) x2	y.

15. Написать уравнение параболы с вершиной в начале координат, если известно, что : а) парабола расположена в левой полуплоскости симметрично относительно оси Ох и

p 12 ; б) парабола расположена симметрично относительно

оси Оy и проходит через точку М(4; 8);			в) фокус параболы
находится в точке F(0;		3).
16. Даны	точки	A(2;1) , B( 1;3) и	C( 2;5) . Найти их
координаты в	новой	системе, если	начало координат
		118

перенесено (без изменения направления осей): 1) в точку А; 2)

вточку В; 3) в точку С.

17.Определить старые координаты начала O новой

системы, если формулы преобразования координат заданы

следующими	равенствами: 1) x x	3 ,	y	y 5;	2)
x x 2 , y y 1; 3) x x , y y 1.
18. Координатные оси повернуты на угол					60 .

Координаты	точек A(2 3; 4) ,	B( 3;0)		C(0;	2 3)

определены в новой системе. Вычислить координаты этих же точек в старой системе.

19. Определить угол , на который повернуты оси, если формулы преобразования координат заданы следующими


равенствами:	1)	x	1	x		3	y ,	y		3	x	1	y ; 2)
равенствами:	1)	x	2	x	2		y ,	y			x		y ; 2)
			2		2				2			2

x 23 x 12 y, y 12 x23 y.

20. Определить тип каждого из следующих уравнений; каждое из них путем параллельного переноса осей координат привести к простейшему виду; установить, какие геометрические образы они определяют:

1)	4x2	9y2	40x 36y 100	0 ;
2)	9x2	16y2	54x 64y 127	0 ;
3)	9x2	4y2	18x 8y 49 0 ;
4)	4x2	y2 8x 6y 11 0 ;
5)	2x2	3y2	8x 6y 11 0 .
21.	Каждое из следующих уравнений привести к
каноническому виду:
1)	14x2	24xy	21y2 4x 18y	139 0 ;
			119

2)	11x2	20xy 4y2	20x 8y 1 0 ;
3)	7x2	60xy 32y2	14x 60y 7 0 ;
4)	50x2	8xy 35y2	100x	8y 67 0 ;
5)	41x2	24xy 34y2	34x	112y 129		0 ;
6)	29x2	24xy 36y2	82x	96y 91 0 ;
7)	4x2	24xy 11y2	64x	42y 51	0	;
3)	41x2	24xy 9y2	24x	18y 36	0 .

																Ответы к п. 4.
1. а) C(2,								3),				R = 4;				б)		C(4, 0),					R = 4;				в)	C(0,		2),			R = 2.
2. а) (x								2)2				( y	3)2			49;						б)	(x		1)2		( y 2)2 25;
		в) (x 1)2										( y 4)2				8;						г) (x 1)2					( y 1)2			4.
3.				а)		а = 5,						b = 3;				б)		F				( 4,0),			F		(4,0);				в)				4	;
3.				а)		а = 5,						b = 3;				б)		F				( 4,0),			F		(4,0);				в)					;
																			1						2								5
																																	5
г) D : x								25			, D : x					25			.		4. а)		x2			y 2	1;		б)	x 2		y	2	1;
г) D : x											, D : x								.		4. а)						1;		б)					1;
			1					4					2			4							9		4					25		9
								4								4							9		4					25		9
				x2			y 2								x2					y2		1;					x2		y 2	1;
в)									1;				г)									1;			д)					1;					е)
			25			16								169					25								5	1
	x 2				y 2			1. 5. а)																											4
	x 2				y 2												C(3, 1),							а = 3,				b =		5 ,					4		,
64			48														C(3, 1),							а = 3,				b =		5 ,			5				,
64			48																														5
	D1 : 2x					3		0,				D2 : 2x				15					0;	б)			C( 1,2),				а = 5,			b = 4,
		3		, D : 3x							28		0,			D		: 3x				22	0; в) C(1,					2),		а = 4,					b
				, D : 3x							28		0,			D		: 3x				22	0; в) C(1,					2),		а = 4,					b
5			1													2
5
									1	, D : y 10 0, D : y 6 0.
= 2 3,									1
= 2 3,
								2			1											2
								2

6.			15			;		63				.				7. 2x2						2xy			2y2		3	0.
6.						;						.				7. 2x2						2xy			2y2		3	0.
			4					4
																					120

7x2

2xy 7 y2

46x 2y 71 0.

а)

пересекает

эллипс;

б)

проходит вне эллипса;

в)

касается эллипса.

10.

а)

а = 3,

b = 4;

б)

(

5,0), F

(5,0);

в)

;

г)

д)

9 .

11.

а)

x 2

y 2

б)

x 2

y 2

в)

x 2

y 2

г)

x 2

y 2

д)

x 2

y 2

е)

x 2

y 2

12.

а)

C(2;

3),

а = 3,

b =

уравнения асимптот:

4х

3у

17 = 0

4х + 3у + 1 = 0, уравнения директрис: 5х

1 = 0 и 5х

19 = 0;

б)

5;1),

а = 8,

b = 6,

уравнения

асимптот:

3х + 4у + 11 = 0

3х 4у + 19 = 0,

уравнения директрис:

х + 11,4 = 0

и х

1,4 = 0;

в)

C(2;

1),

а = 4,

b = 3,

уравнения асимптот:

4х + 3у

5 = 0 и

4х

3у

11 = 0,

уравнения директрис:

у + 4,2

= 0

2,2

= 0.

13.

а)

р = 3;

б)

р = 5.2;

в)

р = 2;

г)

р = 1.2.

( 6

3).

14.

15.

а)

б)

2y;

в) x2

12y;

16.

A(0;0) ,

B( 3;2) , C(

4;4) ;

A(3;

2) ,

B(0;0) , C( 1;2) ;

A(4; 4) ,

B(1;

2) , C(0;0) .

17.

1) (3;5) ;

2) ( 2;1) ; 3) (0; 1) .

;

). 19. 1) 60 ;

30 .

18.

A(3

3;1) ,

, C(3;

20.

Эллиптическое

уравнение,

определяет

эллипс

x 2

1 ,

O (5;

новое начало;

гиперболическое

121

уравнение, определяет гиперболу	x 2	y 2			1, O (3; 2)			-
уравнение, определяет гиперболу	16		9		1, O (3; 2)			-
	16		9
				x 2		y 2
новое начало; 3) эллиптическое уравнение							1,	не
новое начало; 3) эллиптическое уравнение			4		9		1,	не
			4		9

определяет никакого геометрического образа ( является уравнением “мнимого эллипса”); 4) гиперболическое уравнение, определяет вырожденную гиперболу – пару

пересекающихся прямых 4x 2 y 2 0 , O ( 1; 1) - новое начало; 5) эллиптическое уравнение, определяет вырожденный

эллипс (единственную точку) 2x 2

3y 2

0 .

y 2

9x2

16y2

21.

- эллипс; 2)

1 - гипербола;

4y2

вырожденная

гипербола

–

пара

пересекающихся прямых,

уравнения

которых

x 2y

0 ,

0 ; 4) 2x2

3y2

1 - “мнимый эллипс”, уравнение

не

определяет

никакого

геометрического

образа;

2y2

0 - вырожденный эллипс, уравнение определяет

единственную точку –

начало координат;

y 2

1 -

эллипс; 7)

x 2

y 2

1 - гипербола;

y 2

1 - эллипс.

5. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ

ВПРОСТРАНСТВЕ

5.1.Уравнение плоскости

Теорема. В декартовой прямоугольной системе координат каждая плоскость определяется уравнением первой степени.

122

Доказательство. Рассмотрим произвольную плоскость и докажем, что эта плоскость определяется уравнением первой

степени. Возьмем на плоскости

какую-нибудь

точку

M 0 (x0 ; y0 ; z0 ) ;

выберем, кроме этого, произвольный вектор

(не нулевой), перпендикулярный

к плоскости

N {A; B;C} .

Пусть M (x; y; z) -

произвольная

точка.

Она

лежит на плоскости тогда и только тогда, когда вектор

M 0 M

перпендикулярен вектору N (рис. 41)

M 0 M N .

Рис. 41

Условием перпендикулярности двух векторов является равенство нулю их скалярного произведения

M 0 M {x x0 ; y y0 ; z z0} ;

N {A; B;C} ;

N M 0 M

0 => A(x x0 ) B( y y0 )

C(z z0 )

0 .

(5.1)

Это и

есть искомое уравнение плоскости

, т.к.

ему

удовлетворяют х; у; z точки М тогда и только тогда, когда М лежит на плоскости .

Раскрывая скобки, представим уравнение (5.1) в виде

Ax By	Cz	( Ax0 By0 Cz0 ) 0 . Далее, обозначая число
Ax0	By0	Cz0 буквой D, получим
		123

Ax By Cz D 0.

Мы видим, что плоскость действительно определяется уравнением первой степени. Теорема доказана.

Произвольный ненулевой вектор, перпендикулярный плоскости, называется нормальным к ней вектором. Употребляя это название, мы можем сказать, что уравнение

A(x x0 ) B( y y0 )	C(z z0 )	0 есть уравнение плоскости,
проходящей через	точку	M 0 (x0 ; y0 ; z0 )	и имеющей
нормальный вектор N	{A; B;C} .
Уравнение вида
Ax	By Cz	D 0	(5.2)

называется общим уравнением плоскости.

Пример. Составить уравнение плоскости, проходящей через точку M 0 (1;1;1) перпендикулярно вектору N {2;2;3} .

Решение. По формуле (5.1) искомое уравнение таково

2 (х – 1) + 2(у – 1) + 3(z – 1) = 0 или 2х + 2у + 3z – 7 = 0.

Теорема. В декартовых координатах каждое уравнение первой степени определяет плоскость.

Доказательство. Рассмотрим произвольное уравнение

первой степени	Ax	By	Cz D	0 (А, В, С одновременно не
равны нулю).
Пусть	x0 , y0 , z0		произвольная		тройка	чисел,
удовлетворяющая этому уравнению
	Ax0	By0	Cz0	D 0 .		(5.3)

Вычитая из уравнения (5.2) тождество (5.3), получим уравнение

A(x x0 ) B( y y0 ) C(z z0 ) 0 ,

которое по предыдущему представляет собой уравнение плоскости, проходящей через точку M 0 (x0 ; y0 ; z0 ) и имеющей

нормальный вектор N {A; B;C} . Но уравнение (5.2)

равносильно уравнению (5.1), т.к. уравнение (5.1) получается из уравнения (5.2) путем почленного вычитания тождества

124

(5.3), а уравнение (5.2) в свою очередь получается из уравнения (5.1) путем почленного прибавления тождества (5.3). Следовательно, уравнение (5.2) является уравнением той же плоскости. Теорема доказана.

Докажем теперь следующее важное утверждение: если два

уравнения A1x B1 y C1z D1 0 и A2 x B2 y C2 z D2 0

определяют одну и ту же плоскость, то коэффициенты их

пропорциональны.

Действительно,

{A1; B1;C1}

N 2 {A2 ; B2 ;C2 } перпендикулярны к одной и той же

плоскости, следовательно векторы

N2 - коллинеарны,

тогда

A1 A2 m; B1 B2 m;

C2 m .

Пусть M (x; y; z)

- любая точка плоскости. Ее координаты

должны удовлетворять каждому из данных уравнений, поэтому

A1x B1 y C1z D1 0 и A2 x B2 y C2 z D2 0 .

Умножим второе из этих равенств на m и вычтем из первого: получим

D1 D2m 0 или D1	D2m	и	A1	B1	C1	D1	m .
			A2	B2	C2	D2

Тем самым утверждение доказано.

1. Неполные уравнения плоскости. Здесь будем рассматривать частные случаи уравнения первой степени, когда какие-либо из коэффициентов А, В, С, D обращаются в нуль:

1)D 0 : Ax By Cz 0 - определяет плоскость,

проходящую через начало координат,			т.к. числа x		0 ;
y 0 ; z 0	удовлетворяют	уравнению: Ax		By Cz	0.
Следовательно, начало координат принадлежит плоскости.
2) C 0 :	Ax By D 0	-	определяет	плоскость,

параллельную оси Oz (или проходящую через эту ось). В этом


случае нормальный вектор	N	{A; B;C} , имеет нулевую
проекцию на ось Oz ( C	0 );	следовательно, этот вектор
	125

Ax Cz

перпендикулярен оси Oz, а сама плоскость параллельна ей (или проходит через нее).

3) B 0 и C 0 : Ax D 0 - определяет плоскость, параллельную координатной плоскости Oyz (или совпадающую

с ней). В этом случае нормальный вектор		{A; B;C} имеет
	N
нулевые проекции на оси Оу и Oz	( B	0 и C 0 );

следовательно, вектор N перпендикулярен к осям Оу и Oz, а сама плоскость параллельна им (или проходит через каждую из них). Но это и означает, что плоскость, определяемая уравнением Ax D 0 , параллельна плоскости Oyz или совпадает с ней.

По аналогии с предыдущим легко установить, что:

l. Уравнение D 0 задает плоскость, параллельную оси Оу (или проходящую через нее). Уравнение

задает плоскость,

параллельную оси Ох (или

проходящую через нее).

2. Уравнение By

0 задает плоскость, параллельную

плоскости

Oxz

(или

соввпадающую

ней). Уравнение

0 задает плоскость, параллельную плоскости Оху (или

совпадающую с ней).

2. Уравнение плоскости в “отрезках”. Пусть в

уравнении

плоскости

Ax By Cz D 0 ни один из

коэффициентов А, В, С,

D не равен нулю. Сделав следующие

преобразования

D ;

и вводя обозначения a

;

; c

, получим

(5.4)

126

Это специальный вид уравнения плоскости, называемый

уравнением плоскости “в отрезках”. Здесь числа а, b, с имеют простой геометрический смысл, а, b и с - это величины отрезков, которые плоскость отсекает на координатных осях. Чтобы убедиться в этом, достаточно найти точки пересечения плоскости с координатными осями. Точка пересечения плоскости с осью Ох определяется из уравнения этой

плоскости	x	y	z	1 при условии y z 0 . Отсюда x a .
	a	b	с

Таким образом, величина отрезка, отсекаемого плоскостью на оси Ох, действительно равна а. Аналогично, отрезки, отсекаемые плоскостью на осях Оу и Oz, имеют величины, равные соответственно b и с.

Пример. Составить уравнение плоскости, зная, что она

отсекает на координатных осях отрезки

3 ; b

4 ; c

2 .

Решение.

На основании предыдущего получаем искомое

уравнение

или 4x

0 .

Уравнение

плоскости,

проходящей

через

три

различные точки. Пусть на плоскости заданы три различные точки M1(x1; y1; z1) , M 2 (x2 ; y2 ; z2 ) и M 3 (x3 ; y3 ; z3 ) .

Составим уравнение плоскости, проходящей через эти три

точки.

Обозначим

через

x, y, z координаты

произвольной

точки

пространства

и рассмотрим три вектора:

M1M {x x1; y y1; z z1},

M1M 2 {x2 x1; y2

y1; z2

z1},

M1M 3

{x3

x1; y3

y1; z3

z1}. Точка M

лежит

на

плоскости M1M 2 M 3

в том и только в том случае, когда M1M ,

M1M 2 ,

M1M 3 компланарны. Условием компланарности этих

трех векторов является равенство нулю их смешанного произведения. В данном случае имеем

127

		x	x1	y	y1	z	z1
		x2	x1	y2	y1	z2	z1	0 .	(5.5)
		x3	x1	y3	y1	z3	z1
Это и есть искомое уравнение плоскости, проходящей
через	точки M1, M 2 , M 3 ,				так	как		ему удовлетворяют
координаты x, y, z точки				M в том и только в том случае,
когда она лежит в этой плоскости.
4. Нормальное уравнение плоскости. Расстояние от
точки	до плоскости.			Возьмем в			пространстве		Oxyz

некоторую плоскость . Проведем через начало координат прямую n, перпендикулярную к плоскости . Назовем эту прямую нормалью - и отметим буквой Р точку пересечения нормали с плоскостью . На нормали введем положительное направление от начала координат О к точке Р. Если точка Р совпадает с О, т.е. данная плоскоскость проходит через начало координат, то положительное направление нормали выберем произвольно. Обозначим через , , углы, которые

составляет направленная нормаль с осями координат, через р - длину отрезка ОР (рис. 42).


Выведем		уравнение		данной		плоскости	, считая
известными	числа cos		,	cos	, cos	и р. С этой целью
возьмем на плоскости			произвольную точку М и обозначим

через х, у, z	ее	координаты.			Так как, проекция вектора OM

на нормаль равна ОР, то и величина этого отрезка выражается положительным числом р

np n OM

p .

(5.6)

Заметим, что OM

{x; y; z}, отсюда

np n OM

x cos

y cos

z cos .

(5.7)

Из

равенств

(5.6)

(5.7)

следует,

x cos

y cos

z cos

или

x cos

y cos

z cos

p 0 .

(5.8)

128

Это уравнение плоскости носит специальное название:

нормальное уравнение плоскости; в нем cos , cos , cos

суть направляющие косинусы нормали, р - расстояние плоскости от начала координат.

Рис. 42

Пусть, как и ранее, n - нормаль к произвольной плоскости , М* - произвольная точка пространства, d - ее расстояние от

данной плоскости (cм. рис. 42).

Условимся называть отклонением точки М* от данной плоскости число +d, если М* лежит по ту сторону от плоскости, куда идет положительное направление нормали, -d, если М* лежит с другой стороны от данной плоскости. Отклонение точки от плоскости обозначим буквой . Таким образом, d , причем полезно заметить, что d , когда точка М* и начало координат лежат по разные стороны от плоскости, и d , когда точка М* и начало координат лежат по одну сторону от плоскости (для точек, лежащих на

плоскости,		0 ).
	Теорема. Если точка М* имеет координаты (х; у; z*),
а	плоскость		задана	нормальным	уравнением
				129

x cos	y cos	z cos	p 0 , то отклонение точки М* от
этой плоскости задается формулой
		x* cos	y* cos	z* cos	p .

Доказательство. Спроектируем точку М* на нормаль; пусть Q - ее проекция (рис. 42); тогда

PQ OQ-OP ,

где PQ, OQ, OP - это величины направленных отрезков

нормали: PQ , OQ и OP . Но OQ np n OM * , ОР p ; следовательно


	np n OM *			p .		(5.9)
Из ранее доказанного

np n OM * x* cos			y* cos	z* cos	.	(5.10)
Из равенств (5.9) и (5.10) получаем
	x* cos	y* cos		z* cos	p .

Теорема доказана.

Покажем, как привести общее уравнение плоскости к

нормальному виду. Пусть
Ax	By Cz	D	0	(5.2)
- общее уравнение некоторой плоскости, а
x cos	y cos	z cos	p 0 .	(5.8)

- ее нормальное уравнение. Так как уравнения (5.2) и (5.8) определяют одну и ту же плоскость, то коэффициенты этих уравнений пропорциональны, т.е.

A cosα,	B	cos	, C	cos	,	D	p .	(5.11)
Чтобы найти множитель , возведем первые три из этих
равенств в квадрат и сложим. Получим
2 ( A2	B2	C 2 )	cos2	cos2		cos2 .
Так как cos2		cos2	cos2	1 ,	то		1		.



							A2 B 2	C 2
			130

Число называется нормирующим множителем. Для определения знака нормирующего множителя используем последнее из равенств (5.11): D p . Следовательно знак нормирующего множителя противоположен знаку свободного члена нормируемого уравнения. Если D 0 , то знак нормирующего множителя можно выбирать по желанию.

Пример. Даны плоскость 12x 4y 3z 14 0 и точка М(1; 3; 4). Найти отклонение точки М от данной плоскости.

		Решение. Приведем данное уравнение к нормальному
виду.								Найдем							нормирующий			множитель
							1				1			. Умножая данное уравнение на ,


		3		2		4	2	12	2		13
		3				4		12
получим						исходное						нормальное				уравнение		плоскости:
	1	(12x				4 y		3z		14)			0 . Подставляя в				левую	часть	этого
13		(12x				4 y		3z		14)			0 . Подставляя в				левую	часть	этого
13
уравнения								координаты							точки		М,	имеем:
			1		(12 1			4 3		3 4			14)		2 .	Итак,	точка	М	имеет
					(12 1			4 3		3 4			14)		2 .	Итак,	точка	М	имеет
		13

отрицательное отклонение от данной плоскости и удалена от

нее на расстояние d

2 .

5. Угол между двумя плоскостями. Рассмотрим две

плоскости

1 и

2 , заданные соответственно уравнениями

A1x B1 y C1z D1

0 и A2 x B2 y C2 z D2

0 .

При любом расположении плоскостей

пространстве один из углов

между

ними

равен

углу

между их

нормальными

векторами

{A1; B1;C1} и

N 2 {A2 ; B2 ;C2 } и вычисляется по следующей формуле

cos

N1 N2

A1 A2

B1B2

C1C2

(5.12)

A12

B12

C12

A22

B22

C22

Второй угол равен

180

– .

131

6. Условие параллельности плоскостей. Если плоскости

1 и

2 параллельны,

то коллинеарны их нормальные векторы

и N 2 ,

и наоборот. Но тогда

(5.13)

Условие (5.13) является условием параллельности

плоскостей

2 .

7. Условие перпендикулярности плоскостей. Если

плоскости

взаимно перпендикулярны,

то

их

нормальные векторы

и N 2 также перпендикулярны друг

другу

и наоборот.

Поэтому

из формулы

(5.12)

непосредственно

получаем

условие

перпендикулярности

плоскостей

A1 A2

B1B2

C1C2 0 .

(5.14)

5.2.

Уравнение прямой

Линию

пространстве

можно

рассматривать

как

пересечение двух поверхностей и определять заданием двух уравнений. В частности, каждую прямую линию можно рассматривать как пересечение двух плоскостей и соответственно этому определять заданием двух уравнений первой степени.

Пусть заданы некоторая прямоугольная система

координат Oxyz и произвольная прямая L. Обозначим через	1

и2 две различные плоскости, пересекающиеся по прямой L,

заданные соответственно уравнениями

A1x B1 y C1z D1 0 и A2 x B2 y C2 z D2		0 .	(5.15)
Два уравнения вида (5.15) совместно определяют прямую
L в том и только в том случае, когда плоскости	1	и	2	не

параллельны и не совпадают друг с другом, т.е. нормальные


векторы	этих	плоскостей	N1 {A1; B1;C1} и
		132

N2 {A2 ; B2 ;C2} не коллинеарны (коэффициенты A1; B1;C1 не пропорциональны коэффициентам A2 ; B2 ;C2 ).

Уравнения (5.15) называются общими уравнениями прямой.

1. Канонические уравнения прямой. Для решения задач уравнения (5.15) не всегда удобны, поэтому используют специальный вид уравнений прямой.

Пусть дана какая-нибудь прямая L и ненулевой вектор a , лежащий на данной прямой или параллельный ей (рис.43). Вектор a называется направляющим вектором данной прямой. Выведем уравнение прямой, проходящей через данную точку M 0 (x0 ; y0 ; z0 ) и имеющей данный направляющий вектор

a {m;n; p}.

Пусть M (x; y; z)

– произвольная точка. Она лежит на

прямой тогда

только

тогда,

когда

вектор

М 0 М {x x0 ; y

y0 ; z

z0}

коллинеарен

направляющему

вектору a {m;n; p},

т.е. когда координаты вектора

М 0 М

пропорциональны координатам вектора a

z z0

(5.16)

133

Этим соотношениям удовлетворяют координаты каждой точки M (x; y; z) , лежащей на рассматриваемой прямой, и

напротив, если точка M (x; y; z) не лежит на прямой, то ее координаты не удовлетворяют соотношениям (5.16), так как в

этом случае векторы М 0 М и a не коллинеарны и координаты

их не пропорциональны. Таким образом, уравнения (5.16) представляют собой уравнения прямой, проходящей через точку M 0 (x0 ; y0 ; z0 ) в направлении вектора a {m;n; p} .

Рис. 43 Рис. 44

Уравнения (5.16) и является искомыми. Они называются

каноническими уравнениями прямой.

Пусть некоторая прямая задана двумя общими уравнениями:

A1x B1 y C1z D1	0,	(5.17)
A2 x B2 y C2 z D2	0.

Покажем, как составить канонические уравнения этой прямой. Обозначим плоскости, определяемые данными

уравнениями, через		1	и	2 , нормальные векторы этих

плоскостей через	N1 и		N 2 .	Для того чтобы составить
			134

канонические уравнения (5.16), если прямая L задана уравнениями (5.17), необходимо:

1) найти какую-нибудь точку M 0 (x0 ; y0 ; z0 ) L ; для этого следует задать числовое значение одной из неизвестных координат x0 , y0 , z0 и подставить его вместо соответствующей

переменной в уравнения (5.17), после этого две другие координаты определяются в результате совместного решения уравнений (5.17);

2)найти направляющий вектор a {m;n; p} . Так как

прямая L определена пересечением плоскостей

2 ,

то она

перпендикулярна каждому из нормальных векторов

и N 2

(рис. 44). Поэтому в качестве вектора

можно взять любой

вектор,

перпендикулярный векторам

и N 2 , например их

векторное

произведение

N 2 . Так

как

координаты

векторов

N 2

известны:

{A1; B1;C1}

N2 {A2 ; B2 ;C2} , то найдем координаты вектора

;

{m; n; p} .

Пример. Найти канонические уравнения прямой

2 y 4z

2x y 3z 1 0.

Решение. Полагая, например, x0

1, из системы

2 y0

4z0

3z0

получаем y0

2 , z0

1 .

Таким образом,

точка

M 0 (1;2;1)

прямой найдена. Теперь определим направляющий вектор

a .

Имеем:

{3;2;4}

N 2

{2;1; 3} ,

отсюда

т.е. m

10 ,

17 ,

a N1

N 2

{ 10;17;

1} ,

Подставляя найденные значения

x0 ,

y0 ,

m, n, p

135

равенства (5.16), получаем канонические уравнения данной прямой:

x 1	y 2	z 1	.
10	17	1

2. Параметрические уравнения прямой. Иногда прямую полезно задавать не в виде канонических уравнений (5.16), а иначе. Пусть прямая L задана уравнениями (5.16). Обозначим

через

каждое

из

равных

отношений.

Тогда

x x0

t , откуда

mt ,

y y0 nt ,

z z0

pt .

(5.18)

Равенства

(5.18)

называются

параметрическими

уравнениями

прямой

проходящей

через

точку

M 0 (x0 ; y0 ; z0 )

имеющей

направляющий

вектор

a {m;n; p}. В уравнениях

(5.18)

рассматривается

как

произвольно изменяющийся параметр

(

);

x, y,

z –

как функции от t. При изменении

величины

изменяются

так,

что

точка

M (x; y; z)

движется по

данной

прямой.

Параметрические уравнения удобны в тех случаях, когда требуется найти точку пересечения прямой с плоскостью. В

самом деле, пусть непараллельные плоскость				и прямая L
заданы соответственно уравнениями
Ax	By Cz	D 0	и
x x0 mt ,	y y0	nt ,	z z0	pt .

Для определения точки пересечения прямой и плоскости подставим выражения для x, y, z из уравнений прямой L в уравнение плоскости . В результате преобразований

получаем	t	Ax0 By0	Cz0	D	, причем знаменатель
		Am Bn	Cp

дроби не равен нулю, так как плоскость не параллельна прямой. Подставляя найденное значение t в уравнения

136

прямой, находим искомую точку M (x; y; z) пересечения прямой L с плоскостью .

Пример.	Даны прямая	x 2	y 3 z	4	и плоскость
		1	2	1

x 2y z 6	0. Найти точку их пересечения.
Решение.	Задача сводится к определению координат

точки х, у, z из трех данных уравнений (мы имеем два

уравнения				прямой и одно уравнение			плоскости).	Полагая
	x 2		y	3 z 4	t , отсюда	x 2	t , y 3 2t ,	z 4 t .

1		2		1

Подставляя эти выражения в левую часть уравнения данной

плоскости, получим (2 t) 2(3 2t)	(4	t)	6	0 .
Решая это уравнение, находим: t		1 ,	следовательно,
координаты искомой точки будут x 1,	y	1,	z	3 .

3. Уравнение прямой, проходящей через две заданные точки. В аналитической геометрии часто требуется составить уравнение прямой, зная две ее точки. Решим эту задачу в общем виде, считая данными две произвольные точки

M1(x1; y1; z1) и M 2 (x2 ; y2 ; z2 ) .

Для решения задачи достаточно заметить, что в качестве

направляющего

вектора рассматриваемой прямой можно взять

x1 ;

n y2

y1 ;

вектор

M1M 2 ;

отсюда

p z2 z1 и из уравнений (5.16) получим

(5.19)

y1 z2

Это и есть искомые (канонические) уравнения прямой,

проходящей

через

две

данные

точки

M1(x1; y1; z1)

M 2 (x2 ; y2 ; z2 ) .

4. Угол между прямыми.

Рассмотрим две прямые L1

L2 , заданные соответственно уравнениями

x x1

y y1

z z1

x x2

y y2

z z2

137

При

любом расположении прямых

и L2 в

пространстве один из двух углов между ними равен углу

между их направляющими векторами

{m1; n1; p1}

{m2 ; n2 ; p2}, а второй угол равен 180

. Угол

вычисляется по следующей формуле:

cos

m1m2

n1n2

p1 p2

(5.20)

5. Условие параллельности прямых. Для того, чтобы две прямые L1 и L2 были параллельны, необходимо и достаточно, чтобы их направляющие векторы a1 и a2 были коллинеарны, т.е. соответствующие координаты векторов a1 и

a2 были пропорциональны
	m1	n1	p1	.	(5.21)
				.	(5.21)
	m2	n2	p2

Условие (5.21) является условием параллельности двух прямых в пространстве.

6. Условие перпендикулярности прямых. Для того,

чтобы прямые L1 и L2 были перпендикулярны между собой, необходимо и достаточно, чтобы их направляющие векторы

a1 и a2 были ортогональными.
Условие ортогональности двух векторов a1 и	a2
m1m2 n1n2 p1 p2 0 .	(5.22)

является условием перпендикулярности двух прямых в пространстве.

Пример. Найти уравнение прямой, проходящей через точку М(3;2;-1) перпендикулярно двум прямым

L :	x 1	y 7		z 4	;	L :	x 3		y 5	z - 9	.
1	2	- 3	5			2	4	1		- 2
	2	- 3	5				4	1		- 2
Решение.		Составим				уравнение		любой		прямой,

проходящей через точку М

138

x 3	y 2	z 1	.	(*)

m	n	p

Используя условие перпендикулярности искомой прямой к прямой L1 , а затем к прямой L2 получим

2m - 3n 5 p 0,

4m n - 2 p 0.

Из этой однородной системы линейных уравнений с неизвестными m, n, p найдем отношения неизвестных

m : n : p	3 5		:	5	2	:	2	3	1: 24 :14 .
	1	2		2	4		4	1

Подставляя в уравнения прямой (*) вместо m, n, p, пропорциональные им величины, получим искомые уравнения:

y 2

5.3.

Взаимное расположение прямой и плоскости

Пусть

дано

общее

уравнение

плоскости

каноническое

уравнение

прямой

L :

Пусть

{A; B;C} -

нормальный

вектор

плоскости,

a{m;n; p}- направлящий вектор данной прямой.

1.Угол между прямой и плоскостью. Углом между прямой и плоскостью называют любой из двух смежных углов, образованных прямой и ее проекцией на плоскость.

Обозначим угол между векторами N и a через , а угол между плоскостью и прямой L – через . Найдем косинус


угла между векторами N и a

cos			N a		.


		\| N \|		\| a \|
		\| N \|		\| a \|
	139

При этом sin

cos

. Следовательно,

sin

N a

N |

| a |

или в координатной форме,

sin

(5.23)

B 2

C 2

m2 n2 p 2

2. Условие перпендикулярности прямой и плоскости.

Для того, чтобы плоскость

была параллельной прямой

L ,

необходимо и

достаточно,

чтобы

векторы

{A; B;C}

a {m;n; p} были ортогональны между собой.

и a может

Условие ортогональности двух векторов

быть записано как равенство нулю их скалярного произведения


	N a	0
или в координатной форме
Am Bn		Cp 0 .	(5.24)

3. Условие параллельности прямой и плоскости. Для того, чтобы прямая L была перпендикулярна плоскости , необходимо и достаточно, чтобы вектор a был коллинеарен

вектору N .

Условие коллинеарности двух векторов N и a может быть записано как равенство нулю их векторного произведения

				N		a		0
или
			A			B			C	.				(5.25)
										.				(5.25)
			m			n			p
Пример. Составить уравнение плоскости , проходящей
через точку M(-1;2;-3)	параллельно двум прямым
L1 :		x	2				y	6			z 6			;
L1 :			3		4						5			;
			3		4						5
L2	:		x		3 y			4				z	.
L2	:		2					3				1	.
			2					3				1
					140

Решение. Напишем уравнение связки плоскостей с

центром в точке	M
	A(x 1) B( y 2) C(z 3) 0 .	(a)
Используем	условие параллельности плоскости	к

прямой L1 , а затем к прямой L2

3A 4B 5C 0

2A 3B C 0.

Из этой системы однородных уравнений определим отношения коэффициентов А, В, С и затем в уравнение (a) вместо коэффициентов А, В, С подставим пропорциональные им величины:

A : B : C		4	5	:	5	3	:		3	4	11: 13 : 17 ;
		3	1		1	2			2	3
	11(x		1) 13( y			2)		17(z		3)	0 ;

11x 13y 17z 36 0 .

4. Пучок плоскостей. Через всякую прямую в пространстве можно провести бесчисленное множество плоскостей. Совокупность всех плоскостей, проходящих через одну и ту же прямую, называется пучком плоскостей.

Пусть дано уравнение прямой как линии пересечения двух плоскостей

A1x B1 y C1z D1					0,			(5.17)
A2 x B2 y C2 z D2						0.		(5.17)
A2 x B2 y C2 z D2						0.
Составим уравнение
A1x B1 y C1z D1	( A2 x		B2 y	C2 z		D2 )	0 ,	(5.26)
где - произвольное число. При любом						это	уравнение
первой степени, кроме того, при любом						это	уравнение
определяет плоскость, проходящую через прямую (5.17).
Действительно, если точка			M 0		принадлежит			прямой
(5.17), то
A1x0	B1 y0	C1z0		D1	0,
A2 x0	B2 y0	C2 z0		D2		0.
		141

и, следовательно,

A1x0 B1 y0 C1z0 D1 ( A2 x0 B2 y0 C2 z0 D2 0.

Уравнение (5.26) называется уравнением пучка плоскостей, проходящих через прямую (5.17).

Уравнение (5.26) дает любую плоскость пучка, за исключением плоскости

		A2 x B2 y C2 z D2					0.
Пример. Найти проекцию прямой
		2x	3y	4z	1	0			(a)
		x	5y 2z		3	0			(a)
		x	5y 2z		3	0
на плоскость
		3x 4y z 8 0 .							(б)
Решение. Составим уравнение пучка плоскостей,
проходящих через прямую (а)
	2x 3y 4z 1 (x 5y 2z 3) 0 .								(в)
или
(2	)x	(5	3) y	(4	2	)z	(3	1) 0 .
Определим λ , используя условие перпендикулярности
плоскостей:	3(2	) 4(5		3) y	(4	2	)	0 . Откуда	22	.
плоскостей:	3(2	) 4(5		3) y	(4	2	)	0 . Откуда	19	.
									19

Подставив это значение в уравнение (в), найдем уравнение проектирующей плоскости:

2x 3y 4z 1	22	(x 5y 2z 3) 0 ;
	19

60x 53y 32z 47 0 .

Уравнения искомой проекции можно записать как уравнения линии пересечения плоскостей

3x 4 y z 8 0

60x 53y 32z 47 0.

142

Пример. Составить уравнение плоскости, проходящей

через		прямую			3x	2 y	5z	6	0	параллельно прямой
					x	4 y	3z	4	0
	x 1	y - 5	z	1	.
	3	2	- 3		.
	3	2	- 3

Решение. Составим уравнение пучка плоскостей, проходящих через первую из данных прямых:

				3x 2y 5z 6						(x 4y		3z	4)	0 .		(a)
			Преобразуем								это				уравнение
(3		)x		(2	4	) y	(5	3	)z (6		4	)	0 .		Используя
условие				параллельности					прямой			и	плоскости,			получим
3(3		)		2(2	4	)	3(5	3 )		0 .	Отсюда			1 .	Подставляя
найденное значение							в уравнение (a), найдем
				4x	6y	8z	10		0	или	2x		3y 4z 5		0 .
		Пример. Найти расстояние от точки М(1;1;1)													до	прямой
	x	11		y -18		z - 4	.
	2			5		- 2	.
	2			5		- 2
		Решение.				Проведем				через			М	плоскость ,

перпендикулярную к данной прямой и найдем точку Р, где эта плоскость пересекает данную прямую. Искомое расстояние от точки М до данной прямой будет равно расстоянию от точки М до точки Р.

Искомое уравнение плоскости можно записать в виде

A(x 1) B( y 1) C(z 1) 0 .

Эта плоскость должна быть перпендикулярна к данной прямой. По условию перпендикулярности прямой к плоскости имеем

	A	B	C	.
2		5	2	.
2		5	2
Выбирая здесь множитель пропорциональности для
простоты равным единице,		находим A			2 , B	5 , C 2 .
Итак, плоскость имеет уравнение
2(x 1) 5( y 1) 2(z 1)		0 или 2x 5y 2z 5 0 .
Теперь мы должны найти точку Р, в которой эта
плоскость пересекается с данной			прямой.		Для	этого нужно
		143

уравнение данной прямой решить совместно с найденным уравнением плоскости

x 11

y -18

z - 4

t .

- 2

Отсюда

11,

18 , z

2t .

Подставляя

эти

уравнения

уравнение

найденной

плоскости

5y 2z

0 ,

получим

22 25t

90 4t

8 5 0 ;

33t

99 ;

3 .

Координаты точки Р будут равны

5 ,

3 , z

10 .

Искомое расстояние d от точки М до данной прямой, равное расстоянию между точками М и Р, найдется по формуле нахождения расстояния между двумя точками

1)2

(10

1)2

101 .

Пример. Определить условие, при котором две прямые

x x1

y y1

z z1

;

z - z2

лежат на одной плоскости.

Решение. Пусть a1

{m1; n1; p1}

{m2 ; n2 ; p2}

направляющие векторы данных прямых,

M1(x1; y1; z1)

M 2 (x2 ; y2 ; z2 )

точки,

принадлежащие прямым

L1 и

L2 .

Вектор M1M 2

{x2

x1; y2

y1; z2

z1} и направляющие

векторы прямых a1

и a2

компланарны в том и только в том

случае, когда

прямые

L1 и

лежат в

одной

плоскости.

Условием компланарности трех векторов является равенство нулю их смешанного произведения: M1M 2 a1 a2 0 , что в

координатной записи может быть представлено в следующем виде:

144

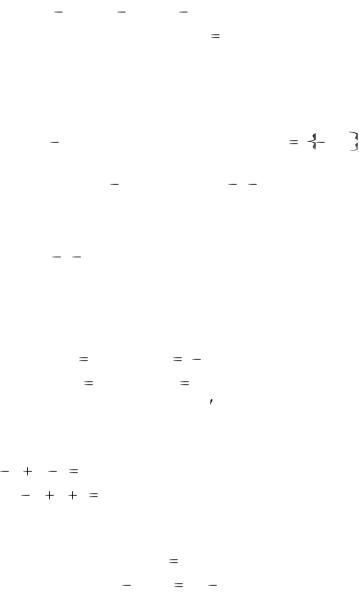
		x2	x1	y2		y1	z2		z1
		m1				n1		p1		0 .
		m2			n2			p2
			Задачи к п. 5
1.	Составить уравнение плоскости, которая проходит
через точку M1(2;1;			1) и имеет нормальный вектор n 1; 2;3
.
2.	Даны точки		M1(3;			1;2)	и	M 2 (4; 2; 1) . Составить
уравнение плоскости,					проходящей через точку M1

перпендикулярно вектору M1M 2 .
3.	Точка P(2;		1; 1)	служит основанием перпендикуляра,

опущенного из начала координат на плоскость. Составить

уравнение этой плоскости.
4.	Написать уравнение плоскости, проходящей через
точку М параллельно векторам								a1	и	a2 , если:
а)	M (1;1;1) ,			a1	{0;1; 2}, a2					{ 1; 0;1};
б)	M (0;1;2) ,			a2	{2; 0;1}, a2					{1;1; 0}.
5.	Написать уравнение плоскости Р , проходящей через
заданные		точки		М1 и М 2				перпендикулярно заданной
плоскости Р, если:
а)	Р:	x	y	1	0,	M1(1; 2; 0),				M 2 (2;1;1);
б)	Р:	2x	y	z	1	0,	M1(0;1;1), M 2 (2;0;1).
6.	Написать уравнение плоскости, проходящей через
точки М1		и M 2	параллельно вектору							a , если:
а)	M1(1; 2; 0),			M 2 (2;1;1),				a	{3; 0;1};
б)	M1(1;1;1),			M 2 (2;3;			1), a			{0; 1; 2}.
7.	Написать уравнение плоскости, проходящей через три
заданные точки			М1, М 2			и M 3 ,			если:
а)	M1(1; 2; 0),			M 2 (2;1;1),				M 3 (3; 0;1);
							145

б) M1(1;1;1), M 2 (0; 1;2), M 3 (2;3; 1).

8.Составить уравнение плоскости, которая проходит

через

точку

M1(3;

2; - 7)

параллельно плоскости

0 .

Определить двугранные углы, образованные

пересечением следующих пар плоскостей:

а) 6x 3y 2z 0, x 2y 6z 12 0;

б) x 2y 2z-3 0, 16x 12y -15z -1 0.

10.

Найти

отрезки,

отсекаемые

плоскостью

24z

0 на координатных осях.

11.

Вычислить площадь треугольника, который отсекает

плоскость 5x

3z 120

0 от координатного угла XOY .

12.

Плоскость

проходит

через

точки

M1(1;2; 1)

M 2 (

3;2;1)

и отсекает на оси ординат отрезок b

3 . Составить

для этой плоскости уравнение “в отрезках”.

13.

Составить уравнения плоскостей, которые проходят

через точку

M1(4;3;2) и отсекают

на координатных

осях

отличные от нуля отрезки одинаковой длины.

14.

Заданы плоскость

Р и точка

М. Написать уравнение

плоскости

Р , проходящей

через

точку М параллельно

плоскости Р, и вычислить расстояние

(P, P ), если:

а)

M (1;1;1);

б)

M (1;1; 2) .

15.Вычислить расстояние d от точки P( 1;1; 2) до

плоскости,		проходящей	через	точки	M1(1; -1;1),
M 2 (	2;1;3),	M 3 (4;-5;- 2) .
	16. На оси OZ найти		точку, равноудаленную от точки
M (1;	2;0) и от плоскости		3x 2y	6z 9 0 .

17.Написать канонические уравнения прямой,

проходящей через точку M 0 (2; 0; 3) параллельно:

146

а)

вектору q

{2;

3; 5};

б) прямой

x 1

;

в)

оси Ох;

г)

оси

Оz;

д)

прямой

е) прямой x

2 t,

2t,

z 1

18.Написать канонические уравнения прямой,

проходящей через две заданные точки М1 и М 2 , если:

а) М1(1;

2;1),

М 2 (3;1;

1);

б) М1(3;

1; 0), М 2 (1; 0;

3).

19. Прямая

L задана общими уравнениями. Написать для

этой прямой канонические уравнения, если:

а)

2 y

б)

2 y

5z 4

5x y

z 0;

2x 3y 2z

20. Составить параметрические уравнения следующих

прямых:

а)

2x 3y z 6 0,

б)

x 2 y z 6 0,

3x 5y 2z 1 0;

2x y z 1 0.

21.

Доказать параллельность прямых:

а)

8 0;

б)

22.

Доказать перпендикулярность прямых:

а)

y 1 z

3x y 5z 1 0,

2 3

2x 3y 8z 3 0;

б)

x y 3z 1 0,

2x y 2z 5 0,

2x y 9z 2 0

2x 2 y z 2 0.

147

23.	Определить косинус угла между прямыми:
а)		x 3 y 2				z		и			x 2					y 3	z	5	;

			1	1	2					1					1		2
			1	1	2					1					1		2
б)			x y 4z 5 0,					и		x 6 y 6z 2 0,
б)			2x y 2z 4 0					и		2x 2 y 9z 1 0.
			2x y 2z 4 0							2x 2 y 9z 1 0.
24.	Доказать, что прямые
L1 :			2x 2 y z 10 0,						и			L2	:		x 7 y 5 z 9
			x y z 22 0
															3		1			4
															3		1			4
параллельны и найти расстояние									(L1, L2 ).
25. Заданы прямая L:							x	1	y			z	1	и точка			M (0;1;2)
25. Заданы прямая L:														и точка			M (0;1;2)
					2				1	0

L (проверить!). Требуется: а) написать уравнение плоскости, проходящей через прямую L и точку М; б) написать уравнение плоскости, проходящей через точку М перпендикулярно прямой L; в) написать уравнение перпендикуляра, опущенного из точки М на прямую L; г) вычислить расстояние

(М , L); д) найти проекцию точки М на прямой L.

									x	3t	2,
26.	Доказать,		что		прямая				y	4t	1,	параллельна
									z	4t	5
плоскости 4x 3y			6z	5			0 .
27.		Доказать, что прямая							5x 3y 2z 5 0,				лежит в
27.		Доказать, что прямая							2x	y z	1	0	лежит в
									2x	y z	1	0
плоскости 4x 3y 7z				7			0 .
28.	Найти точку пересечения прямой и плоскости:
а)		x 1 y 1 z					,	2x 3y z 1 0 ;
а)		1	2	6			,	2x 3y z 1 0 ;
		1	2	6
б)		x 3 y 2 z 1						,	x 2y z 15 0 ;
б)		3	1				5	,	x 2y z 15 0 ;
		3	1				5
в)		x 2 y 1 z 3						,	x 2y 2z 6 0 .
в)		2	3			2		,	x 2y 2z 6 0 .
		2	3			2
							148

29. Составить уравнение прямой, проходящей через точку

M 0 (2;

перпендикулярно к плоскости 6x

30.

Составить уравнение плоскости, проходящей через

точку

M 0 (1; 2;1)

перпендикулярно

прямой

2 y

z 3

31. При каком значении

C прямая

2 y

4x 3y 4z 1 0

параллельна плоскости

2x y Cz 2 0 .

32.

При

каких

значениях

и B

плоскость

0 перпендикулярна к прямой

33.

Найти

точку

Q ,

симметричную

точке

P(4;1;6)

относительно прямой

34.Найти точку Q , симметричную точке P(2; 5;7)

относительно прямой, проходящей через точки M1(5;4;6) и

M 2 (

17;

8) .

35.

Найти

проекцию

точки

P(5;2;

на

плоскость

3z 23 0 .

36.

Найти

точку

Q ,

симметричную

точке

P(1;3;

относительно плоскости

3x y 2z 0 .

37.

Вычислить

расстояние d

от точки

P(2;3; 1)

до

следующих прямых:

а)

;

149

								x			t 1,													2x			2 y						z				3		0,
		б)						y			t			2,									в)	2x			2 y						z				3		0,
		б)						y			t			2,									в)	3x		2 y							2z				17						0.
								z			4t			13;										3x		2 y							2z				17						0.
								z			4t			13;
		38. Составить уравнение плоскости, проходящей через
точку M1(1;2; 3)																	параллельно прямым
				x 1 y 1 z 7																				и		x 5										y 2									z 3						.
																								и																											.
				2						3									3							3													2							1
																					Ответы к п. 5
1.		x 2y 3z 3 0.																						2.				x y 3z 2 0.																								3.
2x y z 6 0. 4. а)																							x 2y z 0; б)																x y 2z 5 0.
5.						а)							x y 3 0;												б)							x 2y 2 0. 6.																					а)
	x 2y 3z 3 0; б) 2x 2y z 1 0. 7. а)																																												x y 3 0;
б) 2x				y				1		0.				8.					2x				3z	27	0. 9.								а)							;			б)			arccos						2	и
б) 2x				y				1		0.				8.					2x				3z	27	0. 9.								а)							;			б)			arccos							и
																																							2										15
		arccos						2	.	10.									a				4,	b	3,			c						1	.				11.							240.						12.
		arccos							.	10.									a				4,	b	3,			c							.				11.							240.						12.
				15																										2
	x		y				2z			1 .									13.				x	y	z	9				0 ,											x					y			z 1			0,

3		3						3
3		3						3
	x	y		z				3		0,				x					y		z		5	0.																											14. а)
2x		y		2				0;		1					;					б)			x	y	0;	1					.								15.							d			4.			16.
																															.								15.							d			4.			16.
										6																2
										6																2
Условию задачи удовлетворяют точки (0;0;																																					2) и						0;0;							82
Условию задачи удовлетворяют точки (0;0;																																					2) и						0;0;							13
																																																		13
17.		а)				x		2					y						z		3	;			б)				x	2									y					z		3			;
17.		а)						2		3									5			;			б)					5									2							1			;
								2		3									5											5									2							1
		в)		x 2							y					z 3				;					г)			x 2										y				z 3						;
		в)																		;					г)																							;
				1						0				0												0											0						1
		д)			x 2 y z 3																;			е)			x 2 y															z 3					.
		д)						4				8						10			;			е)			1										2										.
								4				8						10									1										2						1/ 2
																								150

18.	а)			x	1			y	2								z 1			;			б)			x	3		y	1			z		.
18.	а)			2					3								2			;			б)												.
				2					3								2							2					1				3
19.	а)			x	3/ 2						y			1/ 4							z	;	б)			x		y	1			z	1	.
19.	а)				2									7							4	;	б)		5			12				13		.
					2									7							4				5			12				13
				x		t	1,															x	t	1,
20.	а)			y			7t,											б)				y	3t	2,				23. а)				cos					60 ;
				z			19t		3;													z	5t	1.
б)			cos						4				.			25.						25.	28.	а) (2;-3;6);									б)			прямая
б)			cos										.			25.						25.	28.	а) (2;-3;6);									б)			прямая
									21
параллельна							плоскости;														в)		прямая				лежит				в		плоскости.
29.		x	2				y		3						z	5			.			30.	x	2y			3z		0 .		31.					C	2 .
29.																			.			30.	x	2y			3z		0 .		31.					C	2 .
			6				3									5
32.	A		3 ,				B			9		.				33.					Q(2;		3;2). 34.					Q(4;1;			3). 35.						(1;4;-
32.	A		3 ,				B		2			.				33.					Q(2;		3;2). 34.					Q(4;1;			3). 35.						(1;4;-
									2
7).			36.			Q( 5;1;0).										37.						а)	21;			б)	6;			в)			15.				38.
9x	11y				5z		16 0.

6. ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА

Поверхности второго порядка – это поверхности, которые в прямоугольной системе координат определяются алгебраическими уравнениями второй степени. Геометрическое исследование поверхностей второго порядка производится по заданным уравнениям методом параллельных сечений.

1. Эллипсоид. Эллипсоидом называется поверхность, которая в некоторой прямоугольной системе координат определяется уравнением

х2	y2	z2	1.	(6.1)
a2	b2	c2

Уравнение (6.1) называется каноническим уравнением эллипсоида. Метод параллельных сечений позволяет изобразить эллипсоид как замкнутую овальную поверхность

151

(рис. 45). Величины a, b, c называются полуосями эллипсоида. В случае a b c эллипсоид является сферой.

Рис. 45

2. Однополостный гиперболоид. Однополостным гиперболоидом называется поверхность, которая в некоторой прямоугольной системе координат определяется уравнением

х2	y2	z 2	1.	(6.2)
a2	b2	c2

Уравнение (6.2) называется каноническим уравнением однополостного гиперболоида. Метод параллельных сечений позволяет изобразить однополостный гиперболоид в виде бесконечной трубки, бесконечно расширяющейся по мере удаления от плоскости Oxy (рис. 46). Величины a, b, c называются полуосями однополостного гиперболоида.

3. Двуполостный гиперболоид. Двуполостным гиперболоидом называется поверхность, которая в некоторой прямоугольной системе координат определяется уравнением

152

х2	y 2	z 2	1 .	(6.3)
a2	b2	c2

Уравнение (6.3) называется каноническим уравнением двуполостного гиперболоида. Метод параллельных сечений позволяет изобразить двуполостный гиперболоид как поверхность, состоящую из двух отдельных «полостей», каждая из которых имеет вид бесконечной выпуклой чаши (рис.47). Величины a, b, c называются полуосями двуполостного гиперболоида.

Рис. 46

4. Эллиптический параболоид. Эллиптическим параболоидом называется поверхность, которая в некоторой прямоугольной системе координат определяется уравнением

153

x2	y2
		2z ,	(6.4)
p
	q

где p 0 , q 0 .

Уравнение (6.4) называется каноническим уравнением эллиптического параболоида. Метод параллельных сечений позволяет изобразить эллиптический параболоид в виде бесконечной выпуклой чаши (рис. 48).

Рис. 47

Рис. 48

154

Рис. 49

5. Гиперболический параболоид. Гиперболическим параболоидом называется поверхность, которая в некоторой прямоугольной системе координат определяется уравнением

x2	y2
		2z ,	(6.5)
p
	q

где p 0 , q 0 .

Уравнение (6.5) называется каноническим уравнением гиперболического параболоида. Метод параллельных сечений позволяет изобразить гиперболический параболоид в виде седлообразной поверхности (рис. 49).

6. Конус второго порядка. Конусом второго порядка называется поверхность, которая в некоторой прямоугольной системе координат определяется уравнением

x2	y 2	z 2	0	,	(6.6)
a2	b2	c2

Уравнение (6.6) называется каноническим уравнением конуса второго порядка. Метод параллельных сечений позволяет изобразить конус в виде поверхности, изображенной на рис. 50.

7. Цилиндрическая поверхность. Пусть в плоскости Oxy

лежит некоторая линия L. Проведем через каждую точку линии L прямую, параллельную оси Oz. Множество этих прямых образует некоторую поверхность S, которая называется

цилиндрической. Указанные прямые называются образующими

поверхности S, а линия L – ее направляющей. Аналогично определяются цилиндрические поверхности с образующими,

параллельными осям	Ox и	Oy.
Уравнение цилиндрической поверхности с образующими,
параллельными оси	Oz,	не содержит координаты	z и

совпадает с уравнением направляющей. Например, если направляющей является эллипс

155

x2	y2	1,	(6.7)
a2	b2

то соответствующая цилиндрическая поверхность называется

эллиптическим цилиндром (рис. 51), а (6.7) – ее уравнением.

Рис. 50 Рис. 51

Задачи к п. 6

Установить, какие геометрические образы определяются заданными уравнениями:

1.	z	5 0. 2. x 2y z 1 0.						3.	x2	y2	z2	4.
4.	(x	2)2	y2	(z	1)2	16.	5.	2x2	y2	3z2	0.
6.	x2	4z2	0. 7. x2		2y2		2z2	7 0. 8. x2			4z2	0.
9.	xz	0. 10. xyz		0. 11.		x2	4x	0.	12.	xy	y2	0.
							156

13.Установить, что каждое из следующих уравнений

определяет сферу, найти ее центр С и радиус R:

а) x2	y2	z2	6z 0;
б) x2	y2	z2	4x 2y 2z 19 0.

Установить тип заданных поверхностей и построить их:

14.		x2		y 2			z 2			1.				15.		x2			y 2		z 2	1.
	9		4		25					1.						16			4	36		1.
	9		4		25											16			4	36
16.		x2	y2			z2				1 .				17.		x2			y2		z2.
18.		x2	y2			2az,				a	0.			19.			x2		y2		2az, a 0.
20.	2z		x2			y 2		.		21. x2				2az, a			0.		22. z			2	x2	y2.
20.	2z		x2		2			.		21. x2				2az, a			0.		22. z			2	x2	y2.
					2
23.		x2		y 2			6z.			24.				x2	y2			z2		4.
23.	5		4				6z.			24.				x2	y2			z2		4.
	5		4
25.		x2		y2 z2						4	0.
		Построить заданные цилиндрические поверхности:
26.	y2		z2		4 .				27.			x2			y 2	1.				28.		x2	y2	ax .
26.	y2		z2		4 .				27.		16				9	1.				28.		x2	y2	ax .
											16				9
29.		x2 6z.								30.				z 4 x2.
													Ответы к п. 6
1. Плоскость, параллельная плоскости ОХУ.																							2. Плоскость с
нормальным вектором															1,-2,1 .					Сфера радиуса R					2
нормальным вектором												N			1,-2,1 .				3.	Сфера радиуса R					2
с центром в начале координат.																	4.		Сфера радиуса					R	4 с
центром в точке									С(2,0, 1).						5.		Начало координат.							6.	Ось
Оу.	7.				Пустое множество.												8.			Пара пересекающихся
плоскостей,						параллельных									оси		Оу. 9. Пара						координатных

плоскостей Oyz и Oxy. 10. Тройка координатных плоскостей.

11.	Пара плоскостей	x	0 и x 4 .	12.	Пара плоскостей
y	0 и y x .	13.	а) С(0,0,3),	R	3 ; б) С(2,1, 1),
			157

R	5 . 14.	Эллипсоид.		15. Однополостный гиперболоид.
16.	Двуполостный		гиперболоид			вращения. 17. Конус.
18.	Параболоид вращения.			19.	Гиперболический параболоид.
20.	Эллиптический параболоид.				21.	Параболический цилиндр.
22.	Параболоид		вращения			с	вершиной	(0,0,2).
Гиперболический			параболоид.			24.	Однополостный
гиперболоид		вращения.		25.	Двуполостный			гиперболоид
вращения.

7. ПРЕДЕЛ ПОСЛЕДОВАТЕЛЬНОСТИ

7.1. Множество действительных чисел

Понятие множества является одним из основных неопределяемых понятий математики. Под множеством понимают совокупность (собрание, класс, семейство...) некоторых объектов, объединенных по какому-либо признаку.

Объекты, из которых состоит множество, называются его элементами. Множества принято обозначать заглавными буквами латинского

алфавита	A, B,..., X ,Y,...,			а их элементы —	малыми буквами
a,b,..., x, y,... .
Если элемент x			принадлежит множеству X , то записывают x X
; запись	x	X или	x X	означает, что элемент	x не принадлежит

множеству X .

Множество, не содержащее ни одного элемента, называется пустым, обозначается символом .

Элементы множества записывают в фигурных скобках, внутри которых они перечислены (если это возможно), либо указано общее свойство, которым обладают все элементы данного множества.

Например, запись	A = {1, 3, 15} означает, что множество A состоит
из трех чисел 1, 3 и	15; запись A = { x : 0 x 2 } означает, что

множество A состоит из всех действительных (если не оговорено иное)

чисел, удовлетворяющих неравенству 0				x	2 .
Множество	A называется подмножеством					множества	B ,	если
каждый элемент	множества	A	является		элементом множества			B .
Символически это	обозначают	так	A	B	(« A	включено в	B »)	или

B A («множество B включает в себя множество A »).

158

Говорят,	что множества A и		B равны или совпадают, и пишут
A B , если	A B и B	A . Другими словами, множества, состоящие
из одних и тех же элементов, называются равными.
Объединением (или		суммой)	множеств A и B называется

множество, состоящее из элементов, каждый из которых принадлежит хотя бы одному из этих множеств. Объединение (сумму) множеств обозначают

A	B (или A B ). Кратко можно записать A	B = { x :	x A или
x	B }.
	Пересечением (или произведением) множеств	A и B	называется

множество, состоящее из элементов, каждый из которых принадлежит

множеству	A	и множеству B .	Пересечение (произведение)	множеств
обозначают	A	B (или A B ).	Кратко можно записать A	B = { x :

x A и x	B }.
В дальнейшем, для сокращения записей, будем использовать неко-
торые простейшие логические символы:
	— означает «из предложения			следует предложение »;
	— «предложения	и	равносильны», т.е. из		следует
и из	следует ;

—означает «для любого», «для всякого»;

—«существует», «найдется»;

:— «имеет место», «такое что».

Например:	1) запись	x A :		означает: «для всякого элемента
x A имеет место предложение			»;
2) ( x A	B ) ( x	A или	x	B ); эта запись определяет

объединение множеств A и B .

Множества, элементами которых являются числа, называются числовыми. Примерами числовых множеств являются:

N	1; 2; 3; ...; n; ...				- множество натуральных чисел;
Z0		1; 2; ...; n; ...			- множество целых неотрицательных чисел;
Z	0;		1;	2; ...;	n; ...	- множество целых чисел;
Q		m	: m	Z , n	N	- множество рациональных чисел.
		n

R - множество действительных чисел.

Между этими множествами существует соотношение

N Z0 Z Q R .

Множество R содержит рациональные и иррациональные числа. Всякое рациональное число выражается или конечной десятичной дробью

159

3.1415926...

1.4142356... ,

или бесконечной периодической дробью. Так,	1	0.5 ( 0.500...),

	2
	2

0.333... - рациональные числа.

Действительные числа, не являющиеся рациональными, называются

иррациональными.

Теорема. Не существует рационального числа, квадрат которого равен числу 2.

Допустим, что существует рациональное число, представленное не-

сократимой дробью mn , квадрат которого равен 2. Тогда имеем:

т.е. m2

2n2 .

2 ,

Отсюда следует, что m2

(а значит, и m ) - четное число, т.е. m

. Подставив

2k в равенство m2

2n2 ,

получим 4k 2

2n2 , т.е.

2k 2

n2 .

Отсюда следует, что число

n - четное, т.е. n

2l . Но тогда

дробь

сократима. Это противоречит допущению,

что

дробь

несократима. Следовательно, не существует рационального числа, квадрат которого равен числу 2.

Иррациональное число выражается бесконечной непериодической

дробью. Так, 2 - иррациональные числа. Можно сказать: множество действительных чисел есть множество всех бесконечных десятичных дробей. И записать

R x : x a, 1, 2 , 3... , где a , i 0,1,...,9 .

7.2.Числовые последовательности

1.Числовые последовательности и арифметические действия над ними. Числовые последовательности изучают уже в школе. Примерами таких последовательностей могут служить: 1) последовательность всех членов арифметической и геометрической прогрессий; 2) последовательность периметров правильных п-угольников, вписанных в данную окружность;

3)последовательность x1 1, x2 1.4 , x3 1.41... приближен-

160

ных значений 2 . Уточним и расширим понятие числовой последовательности.

Определение. Если каждому числу п из натурального ряда чисел 1, 2, 3, … , п, … поставлено в соответствие действительное число xn , то множество действительных

чисел x1 , x2 , x3 , …, xn , … называется числовой последовательностью или просто последовательностью.

Числа x1 , x2 , x3 , …, xn , … будем называть элементами (или членами) последовательности, символ xn – общим

элементом (или членом) последовательности, а число п – его номером. Сокращенно последовательность будем обозначать

символом { xn }. Так,	например,					символ 1 n обозначает
последовательность 1,	1	,	1	,...,	1	,... .
	2		3		n

Последовательность считается заданной, если указан способ получения любого ее элемента. Например, формула

х 1	(	1)п	задает последовательность: 0, 2, 0, 2 … . Обращая
п
дробь	1	в десятичную и оставляя один, два,		три и т. д. знака
дробь	3	в десятичную и оставляя один, два,		три и т. д. знака
	3
после запятой, получим последовательность
		x1	0.3, x2 0.33, x3 0.333,..., x3	0.333...3,... .

По самому определению, последовательность содержит бесконечное число элементов: любые два ее элемента отличаются, по крайней мере, своими номерами.

Введем арифметические действия над числовыми

последовательностями. Пусть даны последовательности xn						и
yn .
Произведением последовательности			xn	на	число	m
назовем последовательность		mx1 , mx2 , mx3 , …, mxn , …;
cуммой	данных	последовательностей			назовем
последовательность x1 y1 ,		x2 y2 , ….,	xn	yn , …;
		161

разностью – последовательность

y1 ,

y2 ,….,

xn yn , …;

произведением

– последовательность

x1 y1 ,

x2 y2 ,….,

xn yn , …;

частным

– последовательность

х1

х2

, ...,

хп

, ...,

у1

у2

уп

если все члены последовательности { yn }

отличны от нуля.

Ограниченные

неограниченные

последовательности.

Определение 1. Последовательность

называется

ограниченной сверху (снизу), если существует число

М (число

m) такое, что любой элемент

этой последовательности

удовлетворяет неравенству xn

(xn

m).

Определение 2.

Последовательность

называется

ограниченной, если она ограничена и сверху и снизу.

Пусть

max

. Тогда условие ограниченности

последовательности можно записать в виде

Определение 3.

Последовательность

называется

неограниченной, если для любого положительного числа А

существует элемент	xn	этой последовательности,
удовлетворяющий неравенству		xn	A.

7.3.Сходящиеся последовательности

1.Понятие сходящейся последовательности.

Определение. Число а называется пределом

последовательности xn ,			если для любого положительного
числа	ε существует номер			N	такой, что при n N
выполняется неравенство
		xn	a	.	(7.1)

С помощью логических символов это определение можно записать в виде

162

(

0) ( N ) ( n N ) :

xn a

Последовательность, имеющая предел, называется сходящейся. Последовательность, не являющаяся сходящейся,

называется расходящейся.

Если последовательность xn сходится и имеет своим пределом число а, то символически это записывается так:

lim xn

или

при

(7.2)

Пример.

Используя

определение

предела

последовательности, докажем, что

lim

Возьмем

любое

число

0 .

Так

как

то

для

нахождения

значений n,

n 1

удовлетворяющих неравенству

достаточно решить

неравенство

1/ n

откуда получаем

) .

Следовательно, в качестве N

можно взять целую часть числа

)

, т.е.

Тогда

неравенство

будет выполняться при

всех

Этим и доказано,

что

lim

З а м е ч а н и е. Неравенство (7.1) равносильно

неравенствам

или

которые означают,

что элемент xn

находится в

-окрестности

точки а, точнее, существует номер

N такой, что все элементы

xn с номерами

N находятся в этой ε-окрестности.

Основные

свойства

сходящихся

последовательностей.

Теорема 1. Сходящаяся последовательность имеет

только один предел.

Теорема 2. Сходящаяся последовательность ограничена.

163

За м е ч а н и е. Ограниченная последовательность может

ине быть сходящейся.

Теорема 3. Сумма (разность) двух сходящихся последовательностей xn и yn есть сходящаяся последовательность, предел которой равен сумме (разности)

пределов последовательностей				xn	и	yn .
	Теорема	4.	Произведение			двух	сходящихся
последовательностей			xn	и	yn	есть	сходящаяся

последовательность, предел которой равен произведению пределов последовательностей xn и yn .

Теорема 5. Частное двух сходящихся последовательностей xn и yn при условии, что предел yn отличен от нуля, есть сходящаяся последовательность, предел которой

равен частному пределов последовательностей xn и						yn .
Пример.	Найти lim		2n2	n 1	.
			3n2	1
	n
Решение.	При n	числитель и знаменатель				дроби

стремятся к бесконечности, следовательно, применить теорему о пределе частного нельзя, так как в условии этой теоремы предполагается существование конечных пределов. Поэтому сначала преобразуем данную последовательность, разделив

числитель и знаменатель на n2 . Затем, применяя теоремы о пределе частного и о пределе суммы, найдем

2 1/ n 1/ n

lim (2

1/ n

1/ n2 )

lim

3n2

1/ n2

1/ n2 )

lim (3

lim 2

lim (1/ n)

lim (1/ n2 )

lim 3

lim (1/ n2 )

Теорема 6 (предельный переход в неравенствах). Если

элементы сходящейся последовательности

xn , начиная с

некоторого

номера,

удовлетворяют

неравенству

164

(xn

b),

то

и предел а этой последовательности

удовлетворяет неравенству

b (a

b).

С л е д с т в и е. Если элементы сходящихся

последовательностей

начиная с некоторого

номера, удовлетворяют неравенству

yn , то их пределы

удовлетворяют неравенству lim xn

lim yn.

З а м е ч а н и е. Из строгого неравенства

yn ,

вообще

говоря, не вытекает строгое же неравенство

lim xn

lim yn ,

а только, по-прежнему, вытекает нестрогое

lim xn

lim yn.

Теорема 7 (предел промежуточной переменной). Пусть

даны

три последовательности

zn ,

причем

для всех

n, и пусть последовательности

xn и

имеют

один

тот

же

предел

а.

Тогда

последовательность

также имеет предел а.

3. Бесконечно малые и бесконечно большие

последовательности.

Определение

Последовательность

, имеющая

предел, равный нулю, называется бесконечно малой.

Нетрудно видеть, что для того, чтобы последовательность

имела

предел

а,

необходимо и достаточно,

чтобы

n , где

есть бесконечно малая.

Определение 2. Последовательность

называется

бесконечно большой, если для любого положительного числа А

существует номер N такой, что при n					N выполняется
неравенство	n	A. При этом пишут
неравенство	n	A. При этом пишут
		lim	n	.			(7.3)
		n	n
		n
Символическая запись определения бесконечно большой
последовательности: ( A 0) (				N ) ( n	N ) :	n		A.
последовательности: ( A 0) (				N ) ( n	N ) :	n		A.
			165

Если бесконечно большая последовательность

n ,

начиная с некоторого номера, принимает только положительные или только отрицательные значения, то пишут

	lim	n
	n	n
	n
	или соответственно
	lim	n
	n	n
	n

(7.4)

. (7.5)

Таким образом, из (7.4), так же как и из (7.5), следует (7.3). Пример последовательности ( 1)n n показывает, что

может иметь место соотношение (7.3), в то время как не имеет места ни (7.4), ни (7.5).

Теорема 8. Если	n	бесконечно большая
	n

последовательность и все ее члены отличны от нуля, то

последовательность			1		бесконечно малая, и обратно,

			n
			n
если	n	бесконечно малая последовательность и					n	0 ,
	n						n
то последовательность				1		бесконечно большая.

				n
				n
	Теорема 9. Сумма и разность двух бесконечно малых
последовательностей				есть		бесконечно	малые
последовательности.
	Теорема 10. Произведение					ограниченной последовате-

льности на бесконечно малую есть бесконечно малая последовательность.

7.4.Монотонные последовательности

1.Определение и признак сходимости монотонных последовательностей.

Определение.	Последовательность xn называется
возрастающей, если	xn xn 1 для всех n; неубывающей, если

166

xn xn 1 для всех n; убывающей, если xn	xn 1 для всех n;
невозрастающей, если xn xn 1 для всех	n.

Все такие последовательности объединяются общим названием: монотонные последовательности. Возрастающие и убывающие последовательности называются также строго монотонными.

Рассмотрим примеры монотонных последовательностей.

1.Последовательность 1, 1/2, 1/3, . . , 1/n, . . . убывающая

иограниченная.

2.Последовательность 1, 1, 1/2, 1/2, 1/3, 1/3, . . . 1/n, 1/n, . .

. невозрастающая и ограниченная.

3.Последовательность 1, 2, 3, . . . n, . . . возрастающая и неограниченная.

4.Последовательность 1, 1, 2, 2, 3, 3, . . . n, n, . . .

неубывающая и неограниченная.

5.Последовательность 1/2, 2/3, 3/4, . . ., n/(n+1), . . .

возрастающая и ограниченная.

Отметим, что монотонные последовательности ограничены, по крайней мере, с одной стороны: неубывающая

последовательности – снизу ( xn x1 для всех n), невозрастающие – сверху ( xn x1 для всех n). Оказывается,

что если монотонная последовательность ограничена с обеих сторон, т. е. просто ограничена, то она сходится. Немонотонные последовательности этим свойством не обладают. Например, немонотонная последовательность

1 n	ограничена, но не сходится (см. замечание к теореме 2
из п.	7.3). Имеет место следующая основная теорема о

монотонных последовательностях.

Теорема. Монотонная ограниченная последовательность сходится.

З а м е ч а н и е. Ограниченность монотонной последовательности является необходимым и достаточным условием сходимости. В самом деле, если монотонная последовательность ограничена, то в силу сформулированной

теоремы	она	сходится;	если	же	монотонная
		167

последовательность сходится, то по теореме 2 из п. 7.3 она ограничена.

2. Число е. Рассмотрим последовательность xn с общим

		1 n		1 1 1 , 1	1	2			1 n
членом xn	1		:			,...,	1			,... .

		n			2				n
Докажем, что она сходится. Для								этого достаточно
доказать,	что последовательность					xn	-	возрастающая и

ограничена сверху. Применив формулу бинома Ньютона, получим

xn	1	n	1	n(n 1)	1	n(n 1)(n			2)	1	...
xn	1	n	n	2!	n2	3!					...
			n	2!	n2	3!				n3
...	n(n		1)(n	2)... n	9n	1)	1	.
...								.
				n!			nn

Представим это выражение в следующей форме:

	xn	2			1			1			1					1		1		1					1		2		...
	xn	2						1			n							1		n					1				...
					2!						n				3!					n							n							(7.6)
		1			1							2									n 1													(7.6)
	...	1		1	1					1		2							1		n 1					.
	...			1						1									1							.
			n!			n							n											n
Аналогичным образом представим xn																				1 :
xn 1		2		1	1					1							1		1			1					1					2	...
xn 1		2		2!	1				n			1			3!				1				n		1		1			n		1	...
				2!					n			1			3!								n		1					n		1
	1				1										2														n
...				1								1													1						.
...	n 1 !			1			n 1					1					n 1								1			n 1			.
Заметим теперь, что										1				k	<				1						k				при			0	k	n .

														n										n	1
														n										n	1
Поэтому каждое слагаемое в выражении для xn																																	1 больше
соответствующего слагаемого в выражении для																																xn	и,	кроме
того, у xn	1	по		сравнению											с				xn добавляется еще															одно
												168

положительное слагаемое. Следовательно, xn < xn 1 , т.е. последовательность xn возрастающая.

Для доказательства ограниченности сверху данной последовательности заметим, что каждое выражение в круглых скобках в соотношении (7.6) меньше единицы. Учитывая

также, что	1		1			при			n		2 , получаем

		n!		2n	1
		n!		2n	1
	xn		2		1		1		...	1				1 1	1	1		...				1	.

					2!		3!				n!				2	22					2n 1
					2!		3!				n!				2	22					2n 1
Используя формулу суммы геометрической прогрессии,
придем к неравенству								xn		1		1		1/ 2n		3	1			<		3.
придем к неравенству								xn		1			1	1/ 2		3	2n		1	<		3.
													1	1/ 2			2n		1
Таким			образом, доказано, что последовательность
1 1/ n n			возрастающая и ограничена сверху. По теореме
она имеет предел. Этот предел обозначают буквой																				е.		Итак, по
определению,									1	n
			e		lim		1			.
			e		lim		1		n	.
				n					n

Отметим, что число е играет большую роль во многих вопросах математики. Оно, в частности, является основанием

натуральных логарифмов. Отметим, что так как	xn	3 и	из
(7.6) непосредственно очевидно, что 2 xn ,	то	число	е

заключено в пределах 2 e 3. Доказано, что число е иррациональное.

Задачи к п. 7

Написать первые пять членов последовательностей:

1 ( 1)n

. 2) x

n(1 ( 1)n ). 3)

3n 5

2n 3

Какие

из

последовательностей

являются

ограниченными:

( 1)n

sinn . 4) (1)n

1n .

. 2)

2n .

169

	5)			n		.		6)		1 .		7) ln n .

				n	1
3.	Известно,							что		lim		2n	3			2.		Найти номер					N,		начиная
3.	Известно,							что		lim		n	1			2.		Найти номер					N,		начиная
										n		n	1
с	которого				выполняется							неравенство							2n	3		2			,	где
																			2n	3

																			n	1
																			n	1
	0,1;		0,01;				0,001.
4.	Доказать,							что:		1)	lim		n		1	0.		2)	lim		2n2		3n		1	2		.
4.	Доказать,							что:		1)	lim			n2		0.		2)	lim		3n2						3	.
											n			n2					n		3n2		7n 8				3
3)	lim	(		1)n				0.		4)	lim			3n		1	1.
3)	lim			n				0.		4)	lim			3n			1.
	n			n							n			3n
		Установить, какие из заданных последовательностей
являются бесконечно большими:
															1) n .								n	.
5.	1)		xn		2				n .	2) xn				n(				3)	xn		nsin		n
5.	1)		xn		2				n .	2) xn				n(				3)	xn		nsin		2
																							2
	4) xn				lg(lgn),					n	2.

6. Доказать, что последовательности являются бесконечно малыми:

1)				(	1)n	.		2)		1	при		k	0 . 3)			2n			.
										nk							n2
		1			5 n
		1			5 n														1
		7.				Доказать, что последовательность an														является
бесконечно большой при											a	1		и	бесконечно малой при
бесконечно большой при											a	1		и	бесконечно малой при
	a		1.
	a		1.
				Вычислить пределы:
8.			lim		5n 1	.	9.	lim	3n2		7n 1		.	10.	lim	2n 3		.
8.			lim			.	9.	lim					.	10.	lim	1 n2		.
			n		7 9n			n 2 5n 6n2							n	1 n2

170

11. lim	2n3 4	. 12. lim	2n 1	1 2n3	.
	5 n2		5n 7	2 5n3
n		n

13.lim n cosn . n 5n 11 10n

14.Доказать монотонность последовательностей:

1)		n		. 2)		n	.	3)		n 1		. 4) n2 .			5)	3n	1	.
		2n	1			5n				n						3n
15.		Доказать,			что последовательность									2n		сходится, и
15.		Доказать,			что последовательность									n !		сходится, и
														n !
найти ее предел.
								Ответы к п. 7
2.	1), 3), 5), 6).					3.		N	10,		100,		1000. 5.		1),	4).	8. 5/9.
9.	1/2.		10.		0.	11.		.	12.		0.		13. 1/5.

8.ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ

Всредней школе начато изучение важнейшего понятия математического анализа – понятие функции. В этом разделе будет введено понятие предела функции, а также понятие непрерывности функции.

8.1. Классификация функций

Основными элементарными функциями называют следующие функции.

1) Показательная функция y a x , a 0 , a 1. На рис.52 пока-

заны графики показательных функций, соответствующие различным основаниям степени.

171

Рис. 52

2) Степенная функция y x , R . Примеры графиков сте-

пенных функций, соответствующих различным показателям степени, предоставлены на рис. 53.

3) Логарифмическая функция y loga x , a 0 , a 1; Графики

логарифмических функций, соответствующие различным основаниям, показаны на рис. 54.

172

Рис. 53

4) Тригонометрические функции y sin x , y cos x , y tg x , y ctg x ; Графики тригонометрических функций имеют вид, показанный на рис. 55.

Рис. 54

173

Рис. 55

5) Обратные тригонометрические функции y arcsinx , y arccos x , y arctg x , y arcctg x . На рис. 56 показаны графики обратных тригонометрических функций.

174

Рис. 56

Функция, задаваемая одной формулой, составленной из основных элементарных функций и постоянных с помощью конечного числа арифметических операций (сложения, вычитания, умножения, деления) и операций взятия функции от функции, называется элементарной функцией. Примерами элементарных функций могут служить функции

tg x

x3 ) .

3cos x ;

arcsin

;

lg(2

8x2

Примерами неэлементарных функций могут служить функции

signx

( 1)n

x2n 1

3! 3

5! 5

7! 7

(2n

1)! (2n 1)

Имеет место следующая классификация элементарных

функций.

Функция вида

P(x) a xm

a xm 1 ...

где

m 0

m 1

– целое число,

а0,

а1, ..., аm

– любые числа,

называемые

коэффициентами

(а0 ≠ 0), называется целой рациональной

функцией или алгебраическим многочленом степени т.

Многочлен первой степени называется также линейной функцией.

2) Функция, представляющая собой отношение двух

целых	рациональных	функций
	175

	a xm	a xm 1	...	a	m 1			x	a	m
R(x)	0	1									, называется дробно-
	b xn	b xn 1	...	b		1	x		b

	0	1		n					n

рациональной функцией. Совокупность целых рациональных и дробно-рациональных функций образует класс рациональных функций.

3) Функция, полученная с помощью конечного числа суперпозиций и четырех арифметических действий над степенными функциями как с целыми, так и с дробными показателями и не являющаяся рациональной, называется

иррациональной функцией. Например,


	f (x)		x ,	f (x) x			x,

		5x 2	4x	7		x)3
f (x)		5x 2	4x	7	(5 x
f (x)		3x 2	8x	4	(5 x
		3x 2	8x	4

ит. д. – иррациональные функции.

4)Всякая функция, не являющаяся рациональной или иррациональной, называется трансцендентной функцией. Это,

например, функции			f (x)	sin x ,		f (x) sin x	x и т.д.
			8.2. Предел функции
1.	Предел функции при				x	x0 . Пусть функция			f (x)
определена на некотором множестве Х и пусть точка								x0	X
или	x0	X . Возьмем		из	Х	последовательность		точек,
отличных от		x0 :
		x1 , x2 ,		x3 , …, xn , …,					(8.1)
сходящуюся		к	х0	(предполагается,			что	такая

последовательность существует). Значения функции в точках этой последовательности также образуют числовую последовательность

f (x1 ) , f (x2 ) , f (x3 ) , …, f (xn ) , …,

(8.2)

и можно ставить вопрос о существовании ее предела.

Определение 1. Число А называется пределом функции

176

f (x) в точке

(или при

x0 ),

если для любой

сходящейся

х0

последовательности

(8.1)

значений

аргумента х, отличных от

x0 ,

соответствующая

после-

довательность (8.2) значений функции сходится к числу А.

Символически

это

записывается

так:

lim f (x)

x x0

Функция f (x)

может иметь в точке

х0

только один

предел. Это следует из того, что последовательность

f (xn )

имеет только один предел.

Р а с с м о т р и м п р и м е р ы.

Функция

f (x)

const

имеет предел

в каждой

точке х0

числовой прямой. В самом деле, если (8.1) –

любая

последовательность,

сходящаяся к

x0 , то последовательность

(8.2) имеет вид

С, …, С, ...,

С,

...,

т.е. f (xn )

C . Отсюда

заключаем, что

f (xn )

C при

n → ∞

или

lim

f (x)

С .

2. Функция

f (x)

x имеет в любой точке

х0

числовой

прямой предел, равный x0 . В этом случае последовательности

(8.1)	и	(8.2) тождественны, т.е.				f (xn )	xn . Следовательно,
если		xn	x0 ,	то	f (xn )	x0	при	n	или
lim	f (x)		lim	х	f (x0 ) x0 .
x x0			x x0
	3.	Функция		f (x) sin(1 x)		(рис. 57), определенная для
всех	x	0 , в точке x			0 не имеет предела. Действительно,
возьмем две последовательности значений аргумента									х: 1/π

, 1/(2π), 1/(3π), ..., 1/(пπ), ... и 2/π, 2/(5π), 2/(9π) ..., 2/[(4п 3)π], ...

сходящиеся к нулю. Для них соответствующими последовательностями значений функции являются:

f	1	, f	1	,	f	1	, , f	1	, и
			2			3		n

177

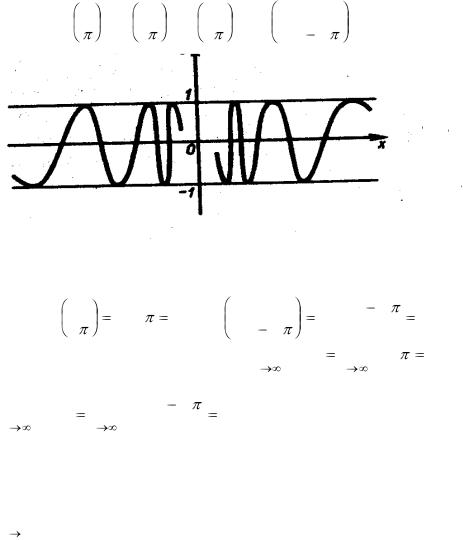
f	2	, f	2	,	f	2	, , f	2		, .
			5			9		(4n	3)

Рис. 57

Так как при любом п

sin n

0 ,

a f

sin

(4n 3)

(4n

то для первой последовательности

lim

f (xn )

lim sin n

для

второй

последовательности

lim f (xn )

lim sin

(4n

Таким образом, для двух сходящихся к нулю последовательностей значений аргумента х соответствующие последовательности значений функции имеют разные пределы. А это по определению предела функции и означает, что

lim f (x) не существует.

x 0

178

4. Функция	f (x)	x2	x 1	имеет в точке	x 0
		x	1

предел, равный 1. Действительно, возьмем любую

последовательность значений аргумента

х,

сходящуюся к

нулю, т. е. lim xn

0 , и

0 , тогда имеем

lim xn

lim f (xn )

lim

lim xn 1

Таким образом,

существует

lim f (xn )

и так как он

не зависит от выбора последовательности {хп}, сходящейся к нулю, то на основании определения предела функции заключаем, что lim f (x) 1.

5.Функция Дирихле, значения которой в рациональных

точках равны единице, а в иррациональных нулю, не имеет предела ни в одной точке x0 числовой прямой. Действительно,

для сходящейся к точке x0 последовательности рациональных

значений аргумента предел соответствующей последовательности значений функции равен единице, а для сходящейся к точке x0 последовательности иррациональных

значений аргумента предел соответствующей последовательности значении функции равен нулю.

Существует другое определение предела функции.

Определение 2. Число А называется пределом функции

f (x) в точке	x x0 , если для любого числа					0 существует
число	0 такое, что для всех					x X ,	x x0 ,
удовлетворяющих			неравенству		х х0	, выполняется
удовлетворяющих			неравенству		х х0	, выполняется
неравенство		f (x)	A	.
неравенство		f (x)	A	.

Используя логические символы, определение 2 можно записать в виде

179

(

0) (

x X , x x0 ,

x x0

f (x)

Отметим,

что неравенства

x x0 ,

х х0

можно

записать в виде

х х0

Первое определение основано на понятии предела числовой последовательности, поэтому его часто называют определением «на языке последовательностей». Второе определение называют определением «на языке ».

Теорема 1. Первое и второе определения предела функции эквивалентны.

2. Предел функции при х → х0 – и при х → х0 +. В

дальнейшем будут использованы понятия односторонних пределов функции, которые определяются следующим образом.

Определение 3. Число А называется правым (левым)

пределом	функции			f (x) в точке				x0 ,		если	для любой
сходящейся к		x0	последовательности						(8.1),		элементы хп
которой	больше			(меньше)			x0 ,			соответствующая
последовательность (8.2) сходится к А.
Символическая запись:
		lim		f (x)	A		lim	f (x)		A .
	x	x0				x	x0
В качестве примера рассмотрим функцию
						1,	если		x	0,
		f (x)		sign x		0,	если		x	0,
						1,	если		x	0.
Она имеет в точке x					0 правый и левый пределы:
		lim sign x			1,	lim sign x				1.
		x	0			x	0

В самом деле, если (8.1) – любая сходящаяся к нулю последовательность значений аргумента этой функции, элементы xn которой больше нуля ( xn 0 ), то sign xn 1 и

180

limsign xn 1.	Следовательно,		lim sign x		1.	Аналогично
n			x	0
устанавливается, что		lim sign x		1.
		x 0
Можно дать равносильное определение односторонних
пределов функции «на языке				»: число		А называется
правым (левым) пределом функции				f (x) в точке x0 , если
для любого	0	существует		0 такое,	что для всех х,

удовлетворяющих неравенствам

x x0

(x0

x x0 ) ,

выполняется неравенcтво

f (x) A

. Символическая запись:

(

0) (

x, x0

x x0

(x0

x x0) :

f (x) A

Связь между

односторонними

пределами

и пределом

функции устанавливает следующая теорема.

Теорема

2. Функция f (x)

имеет в точке

x0 предел

только тогда, когда в этой точке существуют как правый, так и левый пределы, и они равны. В этом случае предел функции равен односторонним пределам.

	3. Предел функции при х→ ∞, при х→	∞ и при х→ +
∞.	Кроме рассмотренных понятий предела	функции при
x	x0 и односторонних пределов существует также понятие

предела функции при стремлении аргумента к бесконечности.

Определение 4. Число А называется пределом функции

f (x) при	x	, если для любой бесконечно большой
последовательности		(8.1)	значений	аргумента
соответствующая		последовательность		(8.2) значений

функции сходится к А.

Символическая запись: lim f (x) A .

Определение 5. Число А называется пределом функции f (x) при x ( x ), если для любой бесконечно большой последовательности значений аргумента, элементы xn которой положительны (отрицательны), соответствующая последовательность значений функции

181

сходится к А.
Символическая	запись:
lim	f (x)	A	lim	f (x)	A .
x			x
Р а с с м о т р и м		п р и м е р.		Пусть	f (x)		1	. Эта
Р а с с м о т р и м		п р и м е р.		Пусть	f (x)			. Эта
							x
функция имеет предел, при			x	равный			нулю.
Действительно, если		хn		бесконечно		большая

последовательность значений аргумента, то соответствующая

последовательность значений функции:	1	,	1	,...,	1	...,

	х1		х2		хп

является бесконечно малой и поэтому имеет предел, равный

нулю, т.е. lim	1	0 .
	x
x
Определения 4		5 даны «на языке последовательностей».
Можно дать равносильные определения «на языке			» и

записать их с помощью логических символов. В качестве

примера		сформулируем определение предела			функции	при
x	.
	Определение 6. Число А называется пределом функции
f (x) при		x	, если для любого числа	0 существует
число		0 такое, что для всех х Х, удовлетворяющих
неравенству x			, выполняется неравенство		f (x) A	.

8.3. Теоремы о пределах функции

Определение предела функции «на языке последовательностей» дает возможность перенести все теоремы о пределах последовательностей на функции. Покажем это на примере двух теорем.

Теорема 1. Пусть функции f (x) и g (x) имеют в точке х0 пределы В и С. Тогда функции f (x) g(x) , f (x) g(x) и

182

f (x)

(при

0 )

имеют

точке

пределы,

равные

g(x)

соответственно В

С,

В С

Теорема

Пусть

функции f (x) ,

g(x) и

h(x)

определены

некоторой

окрестности

точки

x0 , за

исключением, быть может, самой точки

x0 , и функции f (x) ,

h(x) имеют

точке

предел,

равный

А,

т.е.

lim f (x)

lim h(x)

A . Пусть, кроме того,

выполняются

x x0

неравенства

f (x)

g(x)

h(x) . Тогда

lim g(x) A .

xx0

За м е ч а н и е. Теоремы 1 и 2 верны также и в случае,

когда х0

является одним из символов

, +

8.4. Два замечательных предела

Первый замечательный предел

lim

sin x

С помощью первого замечательного предела вычисляются

многие другие пределы.

Пример 1. Найти lim

cos x

Решение.

Знаменатель

дроби

при

стремится к

нулю. Поэтому теорема 1 из

п. 8.3 здесь неприменима. Для

нахождения предела преобразуем данную дробь

lim

cos x

lim

2sin2

(x 2)

lim

sin(x 2)

x 2

lim

sin(x 2)

lim sin(x 2)

1 0

x 2

Пример 2. Найти

lim

tg x

Решение.

Имеем

183

lim

tg x

lim

sin x

lim

sin x

lim

x 0 x

cos x

x 0

x 0 cos x

Пример 3. Найти

lim

0 sin 4x

Решение.

Имеем

lim

5 / 4

1.25.

x 0 sin 4x

0 (sin 4x) /(4x)

lim(sin 4x) /(4x)

2. Второй замечательный предел

lim

Второй

замечательный

предел

имеет

широкое

применение. С его помощью находятся многие другие пределы.

Пример 4. Найти

lim

x)1/ x .

x 0

Решение.

Сделаем

замену переменной,

полагая

1 x

. Тогда очевидно,

что

при

Поэтому

lim (1

x)1/ x

lim (1

)

x 0

Пример 5.

Найти

lim 1

3 / x x .

Решение.

Положим

3t . Тогда при

и t

. Следовательно,

lim (1 3 / x) x

lim(1

1/ t)3t

lim (1

1/ t)t (1

1/ t)t (1 1/ t)t

lim(1

1/ t)t lim(1

1/ t)t

lim(1

1/ t)t

e e e

e3 .

Пример 6. Найти

lim

loga (1

Решение. Для нахождения предела преобразуем данную дробь:

184

lim

loga

lim

loga (1

lim loga (1

1 x

x 0

loga

lim(1 x)1 x .

Но

lim (1

x)1/ x

(см.

пример 4). Поэтому

lim

loga (1

loga e. В частности, lim

ln(1 x)

при a e .

x 0

8.5.Бесконечно малые и бесконечно большие функции

1.Бесконечно малые функции.

Определение 1. Функция f (x) называется бесконечно малой функцией (или просто бесконечно малой) в точке x x0

(или при x	x0 ), если	lim f (x)		0.
	x	x0
Аналогично определяются бесконечно малые функции
при x	x	x			x	x0		и x	x0 .
Можно дать равносильное определение бесконечно малой
функции «на языке		»:		функция			f (x)	называется
бесконечно малой в точке			x	x0 , если для любого					0
существует	0 такое,		что для всех				х	X, x x0 ,
удовлетворяющих неравенству					x	x0	,	выполняется
удовлетворяющих неравенству					x	x0	,	выполняется

неравенство f (x) ; или с помощью логических символов:


(	0 ) (	0 ) ( x X , x x0 ,			x x0	) :	f (x)	\|;
и «на языке последовательностей»: функция								f (x)
называется бесконечно малой в				точке		x x0 , если		для
любой	сходящейся к		x0	последовательности				{ xn }
значений аргумента х,			отличных от x0 ,			соответствующая

последовательность { f (xn ) } является бесконечно малой.

185

Теорема 1. Для выполнения	равенства lim	f (x)	A
	x x0
необходимо и достаточно, чтобы	функция (x)	f (x)	A
была бесконечно малой при x x0 .

Бесконечно малые функции обладают такими же свойствами, что и бесконечно малые последовательности. Справедлива следующая теорема.

Теорема 2. Алгебраическая сумма и произведение конечного числа бесконечно малых функций при x x0 , а

также произведение бесконечно малой функции на ограниченную функцию являются бесконечно малыми

функциями при		x	x0 .
	Все сказанное о бесконечно малых функциях при			x x0
справедливо и для бесконечно малых функций при				x
x	x	x0	и x x0 .

2. Бесконечно большие функции.

Определение 2. Функция f (x) называется бесконечно большой функцией (или просто бесконечно большой) в точке

x x0	(или при		x	x0 ), если для любого			A	0 существует
0 такое,		что для всех x			X ,	x x0 ,	удовлетворяющих
неравенству		x	x0	, выполняется неравенство \|f (х)\|					A.

В	этом	случае пишут			lim f (x)		и	говорят, что
					x x0
функция стремится к бесконечности при x							x0 , или что она
имеет бесконечный предел в точке x						x0 .
Если же выполняется неравенство f(х)							A	( f(х)	A ), то
пишут	lim f (x)			lim f (x)		и говорят, что функция

x x0	x x0
имеет в точке	x0 бесконечный предел, равный	( ) .

По аналогии с конечными односторонними пределами определяются и бесконечные односторонние пределы:

186

	lim	f (x)	,	lim f (x)	,	lim f (x)	,
x	x0		x	x0	x	x0
	lim	f (x)	.
x	x0
Аналогично определяются бесконечно большие функции
при х	x		.

Между бесконечно малыми и бесконечно большими функциями существует такая же связь, как и между соответствующими последовательностями, т. е. функция, обратная бесконечно малой, является бесконечно большой, и наоборот.

8.6. Сравнение бесконечно малых и бесконечно больших функций

Как было показано, сумма, разность и произведение бесконечно малых функций являются бесконечно малыми функциями. Этого, вообще говоря, нельзя сказать о частном: деление одной бесконечно малой на другую может привести к

различным результатам.

Так,

например,

если

(x) x ,

(x) 2x , то

lim

(x)

lim

(x)

x 0

Если же

(x)

x ,

(x)

x2 , то

lim

(x)

lim

(x)

lim x

x 0

(x)

x 0 x

x 0

(x)

x 0

Рассмотрим правила сравнения бесконечно малых

функций. Пусть при x

x0 функции

(x)

являются

бесконечно малыми. Тогда:

1) если

lim

(x)

0 , то

(x)

бесконечно малая более

(x)

x x0

высокого порядка,

чем

(x)

(говорят также, что

(x)

имеет более

высокий

порядок малости,

чем (x) , при

x x0 ); при

сравнении бесконечно

малых

функций

часто

187

(x) .

используют

символ

(«о

малое»).

Если

функция (x) –

бесконечно малая в точке

более высокого порядка, чем

бесконечно

малая

этой же

точке

(x) ,

то

это

условно

записывается так:

(x)

(x)) ;

2) если

lim

(x)

(А

число), то

(x)

и (x)

(x)

бесконечно малые одного порядка;

3) если

lim

(x)

1, то

(x)

эквивалентные

(x)

бесконечно малые. Эквивалентность обозначается обычно так: (x) ~ (x) .

В некоторых случаях недостаточно знать, что одна из двух бесконечно малых является бесконечно малой более высокого порядка, чем другая. Нужно еще оценить, как высок этот порядок. Поэтому вводится следующее правило:

4) если lim	(x)	A 0 , то (x)	бесконечно малая

	n (x)
x x0

п-го порядка относительно

Существуют аналогичные правила для сравнения

бесконечно малых функций при

также при x

x0 справа и слева.

Р а с с м о т р и м п р и м е р ы.

1. Функции

sin x

являются при

эквивалентными бесконечно малыми, так как

lim

sin x

2. Функции

sin3x

sin x

являются

при

бесконечно малыми одного порядка, так как

lim

sin3x

lim

(3sin3x) /(3x)

3 lim

sin3x

lim

x 0

sin x

x 0

(sin x) / x

x 0 sin x

3.Функция (x) 1 cosx является при x 0

бесконечно малой второго порядка малости по отношению к бесконечно малой х, так как

188

lim

cosx

lim

2sin2 (x / 2)

lim

sin(x / 2)

x / 2

x 0

Если функции

(x)

бесконечно малые в точке

x0 , то функция

(x)

имеет

более

высокий

порядок

малости, чем каждый из сомножителей.

Если

(x) ~

1(x) и

(x) ~ 1(x)

при

существует

lim

(x)

то

(x)

существует и

lim

(x)

причем

lim

(x)

lim

(x)

x x0 1

x x0

(x)

x x0 1 (x)

Пример.

Найти

lim

sin 5x

Решение.

Так как

sin5x ~ 5x ,

x3 ~ x при

0, то

lim

sin 5x

lim

x 0 x

Для

бесконечно

больших

функций

имеют

место

аналогичные правила сравнения. Рассмотрим несколько примеров.

1. Функции

(x)

x) x

(x)

1 x являются при

0 эквивалентными

бесконечно

большими, так

как

lim

(x)

lim(1

(x)

x 0

В этом случае говорят также,

что

(x)

имеют

одинаковый порядок роста при x

x0 .

Функция

(x) x2

является

при

бесконечно большой более низкого порядка, чем

(x)

(имеет менее высокий порядок роста), так как

lim

(x)

lim

1 4 x2

lim

(x)

x 2 x2

Бесконечно

большие

при

функции

189

(x)		2x2		1 ,	(x)	x2	1 имеют одинаковый порядок роста,
так	lim		2x2	1	lim	2	1 x2	2.
			x2	1		1	1 x2
	x				x
	4. Функция				(x)		x4 x 1 является при x		беско-

нечно большой второго порядка по отношению к бесконечно

большой		(x)	x2	1,	так как
lim	x 4	x 1		lim	x 4	x 1	lim	1 1 x3	1 x 4	1.

		2 1)2			x 4	2x 2 1			1 x 4
x (x			x				x 1 2 x 2
		8.7.		Непрерывные функции
Пусть функция				f (x) определена в некоторой окрестности

точки x0 .

Определение 1. Функция f (x) называется непрерывной в точке x0 , если предел функции и ее значение в этой точке

равны, т. е.
lim f (x)		f (x0 ).			(8.3)
x	x0
Так как l i mx	x0 , то	соотношение		(8.3)	можно
x x0
записать в следующем	виде: lim f (x)		f ( lim x),		т.е. для
	x	x0	x	x0

непрерывной функции можно переставить знак функции и знак предела. Приведем равносильное определение непрерывности функции «на языке последовательностей».

Определение 2. Функция f (x) называется непрерывной в точке x0 , если для любой последовательности значений аргумента х: x1 , x2 , x3 , ..., xn , ..., сходящейся к x0 , последовательность соответствующих значений функции:

f (x1 ) , f (x2 ) , f (x3 ) , ..., f (xn ) , сходится к f (x0 ) .

Сформулируем определение непрерывности функции «на языке - ».

190

Определение 3. Функция f (x) называется непрерывной в точке x0 , если для любого 0 существует 0 такое,

что для всех х, удовлетворяющих

неравенству

f (x)

f (x0 )

выполняется неравенство

Эквивалентность этих определений очевидна. Запишем

определение 3, используя логические символы:

f (x) f (x0 )

(

0 ) (

0 ) ( x X ,

x x0

| .

Если

lim

f (x)

f (x0 )

lim

f (x)

f (x0 ) ,

то

x x0

функцию

f (x) называют непрерывной

точке

справа

(слева). Если функция

f (x)

непрерывна в точке x0 и слева и

справа, то она непрерывна в этой точке.

Приведем еще одно определение непрерывности функции, которое по существу является перефразировкой первого определения. Перенесем в равенстве (8.3) f (x0 ) в

левую часть и внесем f (x0 ) под знак предела. Так как условия x x0 и (x x0 ) 0 равносильны, то получаем

			lim		f (x)	f (x0 ) 0.		(8.4)
			(x x0)	0
Разность		x	x0 называется приращением аргумента х в
точке x0	и	обозначается, как правило,					x ,	а разность
f (x) f (x0 )		приращением функции в точке					x0 ,	вызванным
приращением		аргумента			x ,	и обозначается		y . Таким
образом,	x	x	x0 ,	y	f (x0	x) f (x0 ) .
Отметим, что при фиксированной точке							x0	y является

функцией аргумента x . Геометрический смысл приращений ясен из рис. 58. Равенство (8.4) в новых обозначениях принимает вид

lim y 0.

(8.5)

x 0

191

Соотношение (8.5) и является еще одним определением непрерывности функции, которое можно сформулировать так.

Определение 4. Функция f (x) называется непрерывной в

точке x0 , если ее приращение	в этой точке является
бесконечно малой функцией при x	0 .

Рис. 58
Теорема 1. Пусть функции		f (x) и	g(x) непрерывны в
точке х0. Тогда функции	f (x)	g(x) ,	f (x) g(x)	и	f (x)

					g(x)

также непрерывны в этой точке ( последняя при g(x0 ) 0 ).

Теорема 2. Всякая элементарная функция непрерывна в каждой точке, в которой она определена.

Определение 5. Если функция непрерывна в каждой точке интервала (a,b) , то говорят, что функция непрерывна на этом интервале. Если функция непрерывна в каждой точке интервала (a,b) и непрерывна на концах интервала, соответственно справа и слева, то говорят, что функция непрерывна на замкнутом интервале [a,b] .

8.8.Классификация точек разрыва

1.Определение и классификация точек разрыва функции.

192

Определение. Точка			x0	называется точкой			разрыва
функции f (x) ,	если	f (x)	в	точке	х0	не	является
непрерывной.
Разрывы	функций		классифицируются			следующим
образом.
Р а з р ы в	1-го	р о д а.		Точка	x0 называется точкой

разрыва 1-го рода функции f (x) , если в этой точке функция f (x) имеет конечные, но не равные друг другу правый и левый

пределы:

lim

f (x)

lim

f (x) .

x x0

Пример. Для

функции

f (x)

sign x

точка

является

точкой

разрыва

1-го

рода,

так

как

lim sign x

x 0

У с т р а н и м ы й

р а з р ы в. Точка

называется

точкой устранимого разрыва

функции

f (x) , если в этой

точке функция

f (x) имеет конечные,

равные

друг

другу

правый и левый пределы:

lim

f (x)

lim f (x)

f (x0 ).

x x0

Пример. Для

функции

f (x)

( s ix)n/ x

точка

является точкой устранимого разрыва.

Р а з р ы в

2-го

р о д а.

Точка

x0 называется точкой

разрыва 2-го рода функции

f (x) , если в этой точке функция

f (x) не имеет, по крайней мере, одного из односторонних

пределов или хотя бы один из односторонних пределов бесконечен.

Пример. Для функции

f (x)

точка

0 является

точкой разрыва 2-го рода, так как lim

lim

x 0

2. Кусочно-непрерывные функции.

Функция

f (x)

называется кусочно-непрерывной на отрезке

[a,b] ,

если она

непрерывна во всех внутренних точках

[a,b] , за исключением,

193

быть может, конечного числа точек, в которых имеет разрыв 1- го рода и, кроме того, имеет односторонние пределы в точках

а и b. Функция называется кусочно-непрерывной на числовой прямой, если она кусочно-непрерывна на любом отрезке.

Рис. 59

Пример. Функция f (x) [x] кусочно-непрерывна как на любом отрезке, так и на всей числовой прямой. Напомним, что символ [x] обозначает целую часть числа x. График функции f (x) [x] изображен на рис. 59, функция [x] в точках x n ( п = 0, ±1, ±2, ...) непрерывна справа и разрывна слева. Во всех других точках она непрерывна как справа, так и слева.

8.9. Основные свойства непрерывных функций Теорема 1 (об устойчивости знака непрерывной

функции). Пусть функция				f (x)	непрерывна в точке x0 и
f (x0 )	0 . Тогда		существует		0 такое, что для всех
x (x0	, x0	)	функция	f (x)	имеет тот же знак, что
f (x0 ) .
Теорема 2 (первая теорема					Больцано-Коши). Пусть
функция	f (x) непрерывна			на отрезке [a,b] и на концах

отрезка имеет значения разных знаков. Тогда существует точка c (a,b) , в которой f (c) 0 .

194

Сформулированная теорема имеет простой геометрический смысл: непрерывная кривая при переходе из одной полуплоскости, границей которой является ось абсцисс, в другую пересекает эту ось.

	Теорема 3 (вторая теорема Больцано-Коши). Пусть
функция f (x) непрерывна на отрезке [a,b] , причем			f (a) A ,
f (b)	B .	Пусть, далее, С – любое число, заключенное между
А и	В. Тогда на отрезке [a,b] найдется точка с		такая,
что	f (c)	C .

Другими словами, непрерывная функция при переходе от одного значения к другому принимает и все промежуточные значения.

Теорема 4 (первая теорема Вейерштрасса). Если функция f (x) определена и непрерывна на отрезке [a,b] , то она

ограничена на этом отрезке.
З а м е ч а н и е. Теорема неверна, если отрезок			[a,b]
заменить интервалом (а,b). Так, например, функция	f (x)		1

				x
				x
непрерывна на (0,1), но не ограничена, так как lim		1	.
непрерывна на (0,1), но не ограничена, так как lim		x	.
x 0		x

Теорема 5 (вторая теорема Вейерштрасса). Если функция f (x) непрерывна на отрезке [a,b] , то она достигает на этом

отрезке по меньшей мере один раз наибольшего значения М
и наименьшего значения m.
Теорема 6.	Пусть функция z	(x) непрерывна в точке
x0 , а функция	y f (z) непрерывна в точке z0		(x0 ) .

Тогда сложная функция	y	f ( (x))	непрерывна в точке х0 .
Теорема 7. Пусть функция y			f (x) определена, строго
монотонна и непрерывна на некотором промежутке X				и
пусть Y множество ее значений.			Тогда на множестве	Y
обратная функция x	( y)	однозначна, строго монотонна и
непрерывна.

Задачи к п. 8

195

		В задачах 1 3, пользуясь только определением предела
функции, доказать что																				lim f (x)									a и заполнить таблицу:
																			x			x0
																	0,1												0,01														0,001
		(			)

1.	f (x) x2 , x																2,				a 4.
													0
2. f (x)							1	, x							1, a 1.
2. f (x)								, x							1, a 1.
							x		0
							x
3. f (x) lg x, x0														1,						a 0.
	Вычислить пределы следующих выражений:
4.	lim					x2			2						.		5.			lim				x2		3		.	6.						lim			1					3					.
4.	lim														.		5.			lim								.	6.						lim										8 x3			.
	x 0 3x2								5x 1											x 3 x2						3								x 2					2 x						8 x3
		x2					2x 1																(x h)3							x3										lim					8x3			1		.
7. lim													.	8.					lim														.		9.
7. lim				x3									.	8.					lim								h						.		9.									6x 2
x 1									x									h 0																						x		1					5x 1
x 1									x																															x		2					5x 1
																																										2
10.	lim				x2				(a 1)x a											.	11.					lim						x3								x 2
10.	lim							x3					a3							.	11.					lim			2x 2									2x 1
	x a							x3					a3												x				2x 2						1			2x 1
12.	lim					x4				5x						.
12.	lim				x2											.
	x				x2				3x					1
			(x 1)5								(x 2)5 (x n)5
13.	lim																														,			n			H.
13.	lim														x5				n5												,			n			H.
	x	a													x5				n5
14.	lim					3x			1			.		15.					lim						x	1			3			.
14.	lim											.		15.					lim													.
	x				5x				3 x										x		10				x	10

16.	lim					x				x				1			1			(x				1).					17.							lim										2x					.


	x 1								x2					1																						x
	x 1								x2					1																						x					3x					3x			3x

							x2		4					2
18.	lim						x2		4					2			.			19.					lim (					x				a				x ).

								2
	x		0				x	2	9					3										x
							x		9					3
																								196

20. lim ( 4x2														7x			4			2x).
	x
		Используя замечательные пределы, вычислить:
21.	lim				sin 3x					.			22.					lim			sin 7x						.			23.				lim x ctg x.
21.	lim							x		.			22.					lim									.			23.				lim x ctg x.
	x	0						x										x			tg 3x													x	0
24.	lim					3arcsin x									.	25.				lim				1			cos2x						. 26. lim				cos				x				cos		x			.
24.	lim								4x						.	25.				lim								x2					. 26. lim										x2							.
	x 0								4x											x 0								x2							x 0								x2
27. lim					1				ctg x . 28. lim tg																	x		sin				x			. 29. lim				2 2 cos x									.
x		0		sin x														x					2									2			x										4x
																																			x	4
																																				4
																										x				3		2x		1		lim				x2					5		x2	.
30.	lim								x				tg x.					31. lim																. 32.
30.	lim							2	x				tg x.					31. lim								x				2				. 32.						x		2			5
	x																			x																x						2
	x

			2
											1																																	a x
33.	lim(cos x) x											2	.			34.				lim x[ln(2												x)		ln x].		35.			lim					a x			a		.
33.	lim(cos x) x												.			34.				lim x[ln(2												x)		ln x].		35.			lim						x		1		.
	x	0																		x																			x			1			x		1
	Вычислить односторонние пределы:
								x	3													2					x															1

36.	lim										.					37.			lim											.		38.			lim (2				x) x .
36.	lim										.					37.			lim											.		38.			lim (2				x) x .
	x 3							x 3										x 2 4 x2																	x 0
									1

39.						lim 7 2							x .			40.				lim arctg x.
				x 2																x
		Найти пределы:

41.	lim			x3					4x 1							.	42.			lim					tg 2x						.	43.			lim		4x 2						1 x			.
41.	lim							2								.	42.			lim											.	43.			lim			3x				5				.
	x	1 3x						2	x				2							x				sin 4x											x
	x	1 3x							x				2							x				sin 4x

																				2
							7x2					5x				1
44.	lim						7x2					5x				1		.	45.				lim						x					x 2	a 2 .
44.	lim								14x2									.	45.			x	lim						x					x 2	a 2 .
	x				3				14x2							2x						x
																							197

46.

lim

x 2

x 1 1

. 47. lim

sin10x

. 48.

lim

cos2x

sin 9x

x sin x

x 0

			tg x					sin x
49.	lim		tg x					sin x					.				50.					lim					x 2				1				x 2				4x .
49.	lim												.				50.					lim					x 2				1				x 2				4x .
	x	0					x3															x
51.	lim				1									4			.				52.				lim				cos(a					x)			cos(a					x)		.
51.	lim				x			1				x2					.				52.				lim											x								.
	x	2			x			1				x2				4									x	0										x
53.	lim			sin(x							b)				sin(x						b)		.	54.					lim			2x sin x						.
53.	lim																						.	54.					lim									.
	x	0										2x																	x	0 sec2x							1
										sin2				3x
55.	lim									sin2				3x								.		56.				lim					x 2				x		1				x 2		x .

					1			x sin x								cos x
	x	0			1			x sin x								cos x										x
						2x
																										5(x2
57.	lim 5 x 3.										58.					lim x cos x										5(x2						3x		1) .
	x															x		0

								x2
59.	lim				1			x2						1			x		.		60.				lim				x tg x					. 61.					lim		1 2 sin x					.
																											1			cos x												6			x
					1						1			x
	x	0			1						1			x											x	0													x
																																							x
																																							6

			1		3			x		.								3			1 x					3 3x					1	.					lim (sec x								tg x).
62.	lim										63.					lim																		64.
					5																				6x

	x	11						x								x	0																				x
		11						x																													x		2
																																							2
	Определить														порядок										малости										(x)					относительно
(x)		x при x												0:

					3				x3																																1				cosx		.
65.	(x)				3				x3			.		66.						(x)				3 x2							x3 .			67.						(x)	1				cosx
65.	(x)											.		66.						(x)				3 x2							x3 .			67.						(x)
					1					x																																			x
		(x) tgx										sin x.
68.		(x) tgx										sin x.						69.						(x)					sin( x					2					2).
	Задана							функция											f (x). При										каком					выборе параметров,
входящих в ее определение,																								f (x) будет непрерывной?

198

		x2		x	2	,			x 1,				x 1,	x	1,
70.	f (x)		x	1		,			x 1,			71.	f (x)
70.	f (x)		x	1								71.	f (x)
			A,				x		1.				ax2	2,	x 1.
			A,				x		1.
	ax		1,	x				,
72.	ax		1,	x			2	,
72.	f (x)
	sin x			b,	x						.
	sin x			b,	x					2	.

Найти точки разрыва функции, исследовать их характер, в случае устранимого разрыва доопределить функцию «по непрерывности»:

73.	f (x)						1			.		74. f (x)				3x	5	.

					x2 (x				1)							3x	5
75.	f (x)			1		sin x.						76.		f (x)		1	x sin		1		.
				x															x
								x
																							1
77.	f (x)		3 4					x 2 .				78.		f (x)		(x	1)arctg						1		.
77.	f (x)		3 4					x 2 .				78.		f (x)		(x	1)arctg								.
																							x
																cos x,											x			,
																cos x,							2				x		4
			2					x,	0	x	1,												2						4
			2					x,	0	x	1,
79.	f (x)		4					2x,	1	x	2,5,		80.	f (x)			1,							x				,
79.	f (x)		4					2x,	1	x	2,5,		80.	f (x)			1,							x			4	,
			2x				7,		2,5		x	4.					2
																x2	2
																				,							x		.
																				,							x		.
																	16						4
											Ответы к п. 8
4.	2.	5.	2.				6.		.	7.	0.	8. 3x2.			9.	6.	10.					(a				1) / 3a2.

11. 1.4.		12. .					13.		n.	14.		3/5.	15.	1/6.	16.		2 / 2.						17.				2 / 3.
18.	3/2.		19.				0. 20.			7/4.		21. 3.		22.	7/3.		23. 1/						.			24. 3/4.
							2		2 ) / 2.
25.	2.	26. (					2		2 ) / 2.			27.	0. 28.		/	. 29.					2 / 4.						30. 1.
31.	e10 .		32. e10 .						33. e 1/ 2 .				34. 2. 35. a ln a .								36.					+1,			1.
												199


37.		, +		. 38.		+	,	0. 39. 0,			+ .		40.		2 ,		2 .	41.		2/3.
42.	1/2.		43. 1/3.			44.		1/2.		45.	0.	46. 1/2.				47.	–10/9.		48.		2.
49.	1/2. 50. –2. 51. –1/4. 52.												2sin a . 53.				cosb .		54.		1.

55.	9.	56.		1.	57.		25.		58.	5.	59.	1. 60.			2.	61.	3 .	62.		5/3.
63.	–1/9. 64. 0. 65. 3/2.								66.	2/3. 67.			1. 68.		3.	69. 1.70.			A		3 .
71.	a	2 .		72.		b		a 2 .		73.	x1		0,	x2	1		точки разрыва
второго рода.					74.			x	5 3		точка разрыва первого рода.
75.	x	0		точка устранимого разрыва;											f (0) 1. 76.				x	0
точка устранимого разрыва;											f (0)		1.	77.		x1	2, x2			2
точки разрыва второго рода. 78. x													0	точка разрыва первого
рода.		79.	x	2.5			точка разрыва первого рода.										80. x			4
точка разрыва первого рода.

9.ДИФФЕРЕНЦИРОВАНИЕ

9.1.Производная функции

1.Определение производной. Пусть на некотором

промежутке Х определена функция					y	f (x) . Возьмем любую
точку	x0	X и зададим		аргументу			х	в точке		x0
произвольное приращение			x	такое, что точка				x0	x также
принадлежит		X.	Функция			получит		приращение
y f (x0		x) f (x0 ) .
Определение. Производной функции							y	f (x) в точке
x0 называется предел при				x	0 отношения приращения

функции в этой точке к приращению аргумента (при условии, что этот предел существует).

Для обозначения производной функции y f (x) в точке x0 используют символы y (x0 ) или f (x0 ) .

Итак, по определению,

200

f (x0 ) lim	y	lim	f (x0	x)	f (x0 )	.
	x			x
x 0		x 0
Если для некоторого значения x0				выполняется условие

lim		y	или	lim	y	,

		x			x
x	0			x 0
то говорят, что	в	точке	x0	функция		имеет бесконечную

производную знака плюс (или знака минус). В отличие от бесконечной производной определенную выше производную функции иногда называют конечной производной. Если

функция f (x)

имеет конечную производную в каждой точке

X , то производную

(x)

можно

рассматривать как

функцию от

х,

также определенную на

Из определения

производной вытекает и способ ее вычисления.

Пример. Найти производную функции

f (x)

x2 в точке

x0 .

Решение.

Давая аргументу

в точке

x0 ,

приращение

x , найдем соответствующее приращение функции:

f (x0

f (x0 )

(x0

x)2

x02

2x0 x ( x)2

x02

2x0 x ( x)2 .

2x0

( x)2

Составим отношение

и найдем

предел этого отношения при

0 :

lim

2x0

( x)2

2x0 .

Следовательно, производная функции

f (x)

x2 в точке

равна числу 2x0 ,

что в принятых обозначениях можно

записать так:

f (x0 )

2x0 .

201

2.	Геометрический				смысл производной.	Пусть
функция y		f (x) определена на интервале (а,b) и пусть точка
М на графике функции соответствует значению аргумента							x0 ,
а точка Р	значению x0			x . Проведем через точки		М и Р
прямую и назовем ее секущей.
Обозначим через				( x) угол между секущей и осью Ох
(рис. 60).	Очевидно, что этот угол зависит от					х.	Если
существует	lim		( x)	0 ,	то прямую с угловым коэф-
		x 0
фициентом	k	tg	0 , проходящую через точку M (x0 ; f (x0 )) ,
называют предельным положением секущей МР при						x	0
(или при P		M ).

					Рис. 60
	Определение.			Касательной		S	к графику		функции
y	f (x) в точке М будем называть предельное положение
секущей МР при			x	0 , или, что то же, при				P	M .
	Из определения следует, что для существования
касательной		достаточно,			чтобы		существовал		предел
lim ( x)		0 ,	причем		предел	0	равен	углу	наклона
x	0

касательной к оси Ох.

202

Если функция y	f (x) имеет в точке x0	производную,
то существует касательная к графику функции		y f (x) в
точке M (x0 ; f (x0 )) ,	причем угловой коэффициент этой

касательной (т.е. тангенс угла наклона ее к оси Ох) равен


производной		f	(x0 ) .
3. Физический смысл производной.					Предположим, что
функция y f (x)			описывает закон движения материальной
точки	М по прямой линии, т.е. y			f (x)	– путь, пройденный
точкой М от начала отсчета за время х.
Тогда за время			x0 пройден путь	y	f (x0 ) , а за время х1
– путь	y f (x1 ) . За промежуток времени				x x1 x0 точка
М	пройдет		отрезок		пути

y	f (x1 ) f (x0 )		f (x0	x) f (x0 ) (рис. 61).
	Отношение	y	называется средней скоростью движения

		x
		x
(vср)	за время x,	а предел отношения			y	при	x	0

					x
					x
определяет мгновенную скорость точки в момент времени								x0

(vмгн ). Понятие скорости, заимствованное из физики, удобно при исследовании поведения произвольной функции. Какую

бы зависимость ни отражала функция y				f (x) , отношение
	y	есть	средняя скорость изменения	у относительно

	x

изменения			х, а y (x0 ) мгновенная скорость изменения у

при x x0 . Значение производной состоит в том, что при

изучении любых процессов и явлений природы с ее помощью можно оценить скорость изменения связанных между собой величин.

203

Рис. 61

4. Правая и левая производные.

Определение. Правой (левой) производной функции

y f (x) в

точке

называется

правый

(левый) предел

отношения

при

0 (при условии,

что этот предел

существует).

Обозначение:

(x0 )

lim

(x0 )

lim

x 0

Если функция

f (x) имеет в точке

производную, то

она имеет в этой точке правую и левую производные, которые совпадают. Вместе с тем существуют функции, имеющие в данной точке x0 правую и левую производные, но не имеющие

производной в этой точке. Это, например,

функция f (x)

которая имеет в точке

0 правую производную,

равную

f (0)

lim

(при x

x ), и

левую

производную,

равную

(0)

lim

1 (при

x 0

x ),

но

не имеет в

этой

точке

производной,

так

как

f (0)

(0).

9.2.Дифференцируемость функции

1.Понятие дифференцируемости функции в данной

точке.

204

	Определение.		Функция		y f (x)	называется
дифференцируемой в точке x0 , если ее приращение							y в этой
точке можно представить в виде
		y	A x ( x)		x ,		(9.1)
где	А некоторое число,			не зависящее от		x , a	( x) –
функция аргумента		x , являющаяся бесконечно малой при
x	0 , т. е. lim	(	x)	0.
	x 0
	Установим связь между дифференцируемостью функции
в точке и существованием производной в той же точке.
	Теорема 1. Для того чтобы функция y					f (x) была диф-

ференцируема в точке x0 , необходимо и достаточно, чтобы

она имела в этой точке конечную производную.

Таким образом, для функций одной переменной дифференцируемость и существование производной понятия равносильные. Поэтому операцию нахождения производной часто называют дифференцированием.

2. Связь между понятиями дифференцируемости и непрерывности.

Теорема 2. Если функция y f (x) дифференцируема в данной точке x0 , то она и непрерывна в этой точке.

З а м е ч а н и е. Обратное утверждение неверно. Функция может быть непрерывной в точке, но не быть дифференцируемой, т.е. не иметь производной в этой точке.

Примером такой функции служит функция f (x)				x	, которая
непрерывна в точке	x	0 , но не имеет в	этой точке
производной, т.е. не является дифференцируемой.
Если функция	f (x)	имеет производную в каждой точке

некоторого промежутка (дифференцируема в каждой точке этого промежутка), то будем говорить, что функция f (x) дифференцируема на указанном промежутке.

9.3. Дифференциал функции

205


1.	Определение	и	геометрический		смысл
дифференциала. Пусть функция			y	f (x) дифференцируема в
точке	x0 , т.е. ее приращение		у	в этой точке можно

записать в виде суммы двух слагаемых:

y A x

(

x ,

где

lim

( x)

Слагаемое

A x

является при

бесконечно

малой

одного

порядка

(при

0),

оно

линейно

относительно

x .

Слагаемое

(

при

0 –

бесконечно малая более высокого порядка, чем

x .

Таким образом, первое слагаемое (при

является

главной частью приращения функции

f (x) .

Определение.

Дифференциалом

функции

y f (x) в

точке

называется главная,

линейная относительно

x ,

часть приращения функции в этой точке:

A x .

(9.2)

Если

0 , то

A x

0, и поэтому слагаемое A x

уже

не является главной частью приращения

у,

так как слагаемое

( x)

x , вообще говоря,

отлично от нуля.

Однако и в этом

случае по определению полагаем дифференциал функции в

точке x0 равным A x , т.е.				dy 0 .
Учитывая, что A f (x0 ) , формулу (9.2) можно записать
в виде
		dy	f	(x0 ) x .				(9.3)
Пусть	f (x) x . Тогда по формуле (9.3)
dy f (x0 ) x	lim	(x0	x)	x0	x	lim	x	x 1 x x.
dy f (x0 ) x	lim		x		x	lim	x	x 1 x x.
	x 0		x			x 0	x
Поэтому дифференциалом независимой переменной х
назовем приращение этой переменной						dx		x . Соотношение
(9.3) принимает теперь вид
		dy	f	(x0 )dx .				(9.4)
				206

Заметим, что с помощью равенства (9.4) производную f (x0 ) можно вычислить как отношение дифференциала

функции

к дифференциалу dx

независимой переменной,

т. е.

f (x0 )

Дифференциал

функции

имеет

геометрический смысл. Пусть точка

М на графике функции

y f (x)

соответствует значению

аргумента

x0 , точка Р

значению

аргумента

x , прямая

касательная к

графику

f (x) в точке М,

угол

между касательной и

осью Ох. Пусть, далее

MN || Ox, PN || Оу ,

точка

пересечения касательной

MS с прямой PN

(рис. 62). Тогда

приращение функции

равно величине отрезка NP. В то же

время

из прямоугольного треугольника

MNQ

получаем:

f (x0 )

dy , т.е. дифференциал функции dy

равен величине отрезка NQ. Из геометрического рассмотрения видно, что величины отрезков NP и NQ различны. Таким

образом, дифференциал функции y f (x)	в точке	x0	равен
приращению «ординаты касательной»	к графику		этой
функции в точке M (x0 ; f (x0 )) , а приращение функции			y есть
приращение «ординаты самой функции» y	f (x) в точке x0
, соответствующее приращению аргумента, равному		x .

207

Рис. 62
2. Приближенные вычисления	с помощью

дифференциала. Из определения дифференциала следует, что

он зависит линейно от	x и является главной	частью
приращения функции	y. Само же y зависит от	x более

сложно. Во многих задачах приращение функции в данной точке приближенно заменяют дифференциалом функции в этой точке: y dy .

Пример. Покажем, что если		мало,		то можно

использовать приближенную формулу	1	1		/ 2.
Решение. Рассмотрим функцию				При малых
Решение. Рассмотрим функцию	f (x)		x.	При малых
х имеем

( x)

x lim

lim

x x0

x 0

x 0 x( x0

x0 )

2 x0

откуда, положив x0

1 ,

х =

получим

/ 2.

В частности,

1.0003

1.00015 при

= 0.0003.

9.4. Правила дифференцирования.

Производные основных элементарных функций

1. Правила дифференцирования.

Теорема 1. Если функции u

u(x) и

v(x) дифферен-

цируемы в точке х, то сумма, разность, произведение и частное этих функций (частное при условии, что v(x) 0 )

также дифференцируемы в этой точке и имеют место следующие формулы:

208

(u v) u v ,

(u v) u v uv ,

uuv u v.

vv2

Сл е д с т в и е. Если функции u u(x) и v v(x)

дифференцируемы в точке х, то
	d(u v)	du		dv ,		d(u v)			vdu	udv ,
		d	u		v du	u dv		.
		d						.
			v		v2
2. Производная постоянной функции.										Производная
функции	y f (x)	C ,		где		С	–		постоянное число,
выражается	формулой			y 0 .		А,		в	силу	теоремы 1,

постоянный множитель можно выносить за знак производной.

	3. Производные тригонометрических функций.
	1) Производная функции					y	sin x выражается формулой
y	cos x .
	2) Производная функции					y	cos x выражается формулой
y		sin x .
	3) Производная функции					y	tg x выражается формулой
y	1		x		n .

	cos2 x			2
	cos2 x			2
	4) Производная функции					y	ctg x выражается формулой
y	1		(x	n ).

		sin2 x
		sin2 x

4. Производная логарифмической функции.

Производная функции

формулой	y	1		loga e
			x

С л е	д с	т		в и е.
y (ln x)	1 x .

y loga x ( 0 a 1) выражается

1 .

xln a

Если	y loge x ln x , то

5. Производная	показательной функции и обратных
тригонометрических	функций. Пусть функция y f (x)
	209

удовлетворяет условиям теоремы							о существовании обратной
функции и функция		x	( y)			является для нее обратной.
Тогда имеет место следующая теорема.
Теорема 2 (о производной обратной функции). Если
функция y	f (x) имеет в точке						x0 производную f		(x0 ) 0 ,
то обратная функция x			( y) также имеет в соответству-
ющей точке	y0 f (x0 )	производную, причем
	( y0 )				1			.	(9.5)


				f (x0 )
Теорема	имеет	простой					геометрический		смысл.


Рассмотрим в некоторой окрестности точки x0 график функ-
ции	y	f (x) (или обратной функции x	( y) . Пусть точке
x0	на этом графике соответствует точка		М (рис.63). Как из-
вестно,		производная f (x0 ) равна тангенсу угла		наклона

касательной, проходящей через точку М, к оси Ох.

Производная обратной функции	( y0 ) равна тангенсу угла
наклона той же касательной к оси	Оу. Поскольку углы и

в сумме составляют /2, то формула (9.5) выражает очевидный факт:

( y0 ) tg	1	1		1	1		.

	ctg		ctg( 2	) tg		f (x0 )

Рис210. 63

Используя сформулированную теорему, продолжим вычисление производных простейших элементарных функций.

Производная функции

y a x ( 0

выражается

формулой

a x ln a .

С л е д с т в и е 1.

Если

e x ,

то

e x .

e x

С л е д с т в и е

Если

sh x

то

e x

ch x

, функция

sh x называется гиперболическим

синусом,

функция

ch x

называется

гиперболическим

косинусом.

e x

С л е д с т в и е

Если

ch x

то

sh x .

С л е д с т в и е 4. Если

th x

sh x

e x

ch x

e x

то

, функция th x

называется

гиперболическим

ch2

тангенсом.

ch x

e x

С л е д с т в и е 5. Если

cth x

то

sh x

e x

функция

cth x

называется

гиперболическим

котангенсом.

Производная

функции

arcsin x

выражается

формулой

211

1 .

Производная

функции

arc cos x

выражается

формулой

1 .

Производная

функции

arctg x

выражается

формулой

Производная

функции

arc ctg x

выражается

формулой

6. Дифференцирование сложной функции.

Теорема 3. Если функция

(t) , имеет производную в

точке

t0 , а функция

f (x)

имеет производную в


соответствующей		точке x0	(t0 ) , то сложная функция
f ( (t)) имеет	производную		в точке t0 и справедлива
следующая формула:		y (t0 )	f (x0 )	(t0 ) .
З а м е ч а н и е 1. В данной теореме рассмотрена
сложная функция, где у зависит от t				через промежуточную
переменную х.	Возможна и более сложная зависимость с

двумя, тремя и большим числом промежуточных переменных, но правило дифференцирования остается таким же.

Так, например, если y			f (x) , где x		(u) ,	a u	(v)
и v	(t) ,	то производную		y (t) следует вычислять по
формуле	y (t)	f (x) (u)	(v)	(t) .
Пример 1. Вычислить производную функции						y	earctgx .
			212

Решение. Данную функцию можно представить в виде

eu , где

u arctg x .

Тогда

по правилу дифференциро-

вания сложной функции

y (x) y (u) u (x)

Заменяя

на

arctg x ,

окончательно

получим

earctgx

Пример

Вычислить

производную

функции

y tg2

Решение. Данную функцию можно представить в виде

u 2 ,

w x 2 1. По

где

tgv ,

правилу дифференцирования сложной функции получаем

(u 2 ) (tg v) (

) (x 2

y (x)

y (u) u (v) v (w) w (x)

tg x 2

cos2v 2 w

x 2

cos2

x 2

З а м е ч а н и е 2.

Иногда производную приходится

вычислять непосредственно исходя из ее определения. Найдем, например, производную функции

x 2 sin

при

f (x)

при

При

0 производная

вычисляется

по формулам

правилам дифференцирования:

f (x)

x2 sin

(x2 ) sin

sin

2x sin

cos

Этим выражением нельзя воспользоваться при x

0 .

точке x

производную

можно вычислить,

используя

определение производной:

213

f (0)	lim	y	lim	x sin	1	0,
		x			x
	x 0		x 0

т.к. произведение бесконечно малой функции на ограниченную есть бесконечно малая. Таким образом,

	2x sin	1	cos	1	при	x	0,
f (x)	2x sin	x	cos	x	при	x	0,
f (x)		x		x
	0				при	x	0.

Теорема 4 (инвариантность формы дифференциала).

Дифференциал функции у выражается по одной и той же формуле независимо от того, будет ли у рассматриваться как функция от независимой переменной х, или от зависимой переменной х.

7.Логарифмическая производная. Производная

степенной функции. Вычислим производную

функции

y ln

( x 0 ). Так как (ln x)

(ln(

x))

( х)

(последнее равенство получено на основании правила дифференцирования сложной функции), то производная данной функции выражается следующей формулой

y ln

Учитывая эту формулу, вычислим производную

сложной

функции y ln

где

f (x)

дифференцируемая

функция.

Имеем

(x)

или

f (x)

Производная

f (x)

называется логарифмической

производной функции

f (x) .

Для

упрощения

записи при

логарифмическом дифференцировании знак модуля у функции f (x) обычно опускается.

214

Вычислим с помощью логарифмической производной

производную показательно-степенной функции									y		u(x)v( x) ,
где	и	и v –		некоторые функции от			х ( u	0 ), имеющие в
данной		точке		х	производные u (x)		и	v (x) .		Так как
ln y	v(x) lnu(x) ,				то имеем
			y		v(x)lnu(x)	v (x) lnu(x) v(x)			u (x)		.

			y						u(x)
	Отсюда, учитывая, что y					u(x)v( x) , получаем следующую

формулу для производной показательно-степенной функции:

		y u(x)v(x)			v' (x) ln u(x) v(x)			u' (x)	.
		y u(x)v(x)			v' (x) ln u(x) v(x)				.
								u(x)
	Пример. Вычислить производную функции y									x x .
	Решение.	Данную функцию можно представить в виде
y	u(x)v( x) ,	где		u(x)	x	и	v(x) x .			Поэтому
y	x x 1 ln x	x	1	x x (ln x		1).
y	x x 1 ln x	x	x	x x (ln x		1).
			x

Логарифмическая производная очень удобна при нахождении производной степенной функции с любым

вещественным показателем.
Производная	степенной	функции		с	любым
действительным показателем		y x	(		любое
вещественное число) выражается формулой			y	x	1.

8. Таблица производных простейших элементарных функций. Нами вычислены производные всех простейших элементарных функций и мы можем составить следующую таблицу производных.

I.(С)= 0.

			1,			1		1						1	.
II. (x	)	x			в частности	1		1	, (		x )			1
						х		x2

														2 x
III.	(logа х)	=	1		logа е, в частности		(ln х)			=		1	.
III.	(logа х)	=			logа е, в частности		(ln х)			=			.
				x								x
					215

IV.

VI.

VII.

VIII.

(a x )	a x ln a,			в частности, (ex ) ex .
(sin х)	= cos х.
(cos х)	= sin х.
(tg x)	=	1		.

		cos2 x
		cos2 x
(ctg x) =		1			.


			sin2 x

IX.	(arcsin х)	=		1			.



				1		x2
X.	(arccos x)	=				1			.


				1		x2
				1		x2
XI.	(arctg x) =			1		.

			1		x2
XII.	(arcctg x)	=		1				.

				1		x2

XIII. (sh х)= ch х.

XIV. (ch х) = sh х.

1 XV. (th x) = .

ch2 x

1 XVI. (cth x) = .

sh2 x

Формулы, приведенные в таблице, а также правила дифференцирования суммы, разности, произведения, частного и правило дифференцирования сложной функции являются основными формулами дифференциального исчисления. На основе правил и формул дифференцирования можно сделать важный вывод: производная любой элементарной функции также элементарная функция. Таким образом, операция дифференцирования не выводит из класса элементарных функций.

216

9.5.Производные и дифференциалы высших порядков

1.Понятие производной п-го порядка. Как уже

отмечалось, производная f (x) функции y f (x) сама

является некоторой функцией аргумента х. Следовательно, по отношению к ней снова можно ставить вопрос о существовании и нахождении производной.

Назовем f (x) производной первого порядка функции f (x) . Производная от производной некоторой функции

называется производной второго порядка (или второй производной) этой функции. Производная от второй производной называется производной третьего порядка (или

третьей производной) и т.д. Производные, начиная со второй, называются производными высших порядков и

обозначаются


y (x),	y	(x),	y(4) (x), y(5) (x),...,		y(n) (x),...		или
f (x),	f	(x),	f (4) (x),	f (5) (x),..., f (n) (x),...
Производная n-го порядка является производной от
производной	(n – 1)-го порядка, т.е.				y(n)	( y(n 1) ) .
Производные высших порядков имеют широкое
применение		в	физике.	Ограничимся			физическим
истолкованием		второй производной			f	(x) .	Если функция

y f (x) описывает закон движения материальной точки по

прямой линии, то первая производная	f (x) есть мгновенная
скорость точки в момент времени	х, а вторая производная

равна скорости изменения скорости, т.е. ускорению движущейся точки в этот момент.

2.	Формулы	для	n-х производных некоторых
функций.
1)	Вычислим	п-ю	производную степенной	функции
y x	( x 0 )	(	любое действительное	число).

Последовательно дифференцируя, имеем:

217

1 ,

(

1) x

2 ,

(

1) (

2) x

3 ,...,

y (n)

(

1) (

2)...

n .

В частном случае, если

где

натуральное

число, получаем

(x)(m)

m(m 1)(m

m!,

(x)(n)

при

2) Вычислим п-ю производную показательной функции

y a x (0 < a

1). Последовательно дифференцируя, имеем

a x ln a,

a x (ln a)2 ,

... ,

y(n)

a x (ln a)n .

частности,

если

e x ,

то

для любого

(e x )(n)

e x .

3) Вычислим

п-ю

производную функции

sin x .

Последовательно дифференцируя, имеем

cos x

sin

sin x

sin (x

)

sin

cos x

sin x

, ... , y (n)

sin

Таким образом, производную любого порядка от

sin x

можно вычислять по формуле

(sin x)(n)

sin

Например,

(sin x)(10)

sin

sin(x

)

sin x.

4)Аналогично можно получить формулу п-й

производной функции y cos x : (cos x)(n) cos x n		.
	2

3.Формула Лейбница для n-й производной

произведения двух функций. Пусть y u v , где и и v –

некоторые функции от переменной х, имеющие производные любого порядка. Тогда

218

y (n)

(uv)(n)

u (n) v

n u (n 1) v

n (n

u (n

v ...

(9.6)

n (n

1)...(n

...

u (n

k ) v(k )

...

u v(n) .

Формула (9.6) называется формулой Лейбница.

Пример 1.

Вычислить

пятую

производную функции

x5e x .

Решение.

Полагая

e x , найдем u

5x 4 ,

20x3 ,

60x 2 ,

u (4)

x2,

0u (5)

120;

v(4)

v(5)

e x . Подставляя эти

выражения в

формулу (9.6) при

n 5 ,

получаем

y(5)

120 e x

5 120 x ex

5 4

60 x2 ex

5 4 3

20 x3 ex

1 2

1 2 3

5 5 x4 ex

x5ex

ex (120

600 x

600 x2

200 x3

25 x4

x5 ).

Пример

Вычислить

п-ю

производную ( n

2 )

функции

x2 cos x .

Решение.

Полагая

cos x

x 2 ,

найдем

u(n)

cos x

2x,

v(4)

v(5)

...

Подставляя в формулу (9.6), получаем

y(n) cos x

2n cos x

n (n

1) cos

4. Дифференциалы высших порядков.

Определение.

Вторым дифференциалом

от

функции

y f (x) в точке

х называется дифференциал от первого

дифференциала в этой точке и обозначается так:

d 2 y

d (dy) .

219

(t) Ф(x)

Аналогично можно определить дифференциал любого порядка. Отметим, что второй дифференциал и все последующие дифференциалы, в отличие от первого, не обладают инвариантностью формы.

9.6.Параметрическое задание функции

иее дифференцирование

1.Параметрическое задание функции. Пусть даны две функции

x (t) , y (t) (9.7)

одной независимой переменной t, определенные и непрерывные в одном и том же промежутке. Если x

строго монотонна, то обратная к ней функция t

однозначна, также непрерывна и строго монотонна. Поэтому у можно рассматривать как функцию, зависящую от переменной

х посредством переменной

называемой

параметром:

(Ф(x)) .

В этом случае говорят, что функция у от

задана

параметрически с помощью уравнений (9.7).

Отметим,

что

функция

(Ф(x))

непрерывна

силу

теоремы о непрерывности сложной функции.

Пример 1. Пусть

R cost ,

Rsint

). Так

как

функция

R cost

убывает

при

, то

данные

уравнения задают параметрически функцию

от

х.

Если

выразить

через

из первого уравнения и подставить во

второе, то получим искомую функцию переменной х

в явном

виде.

Это

еще

легче

сделать,

если

заметить,

что

R2 (cos2 t

sin2 t)

R2 .

Отсюда

у =

или

у =

x2 .

Так

как

функция

Rsint неотрицательна

для

то перед

220

радикалом выбираем знак плюс: y				R 2	x2 . Если		t	2 ,

то y	R2	x2 .
Таким образом, можно сделать вывод, что						когда		t
изменяется от 0			до 2 , то формулы	x	R cost ,	y	Rsint
определяют		две	функции переменной		х, графики которых
образуют окружность радиуса R.
Пример 2. Пусть x a cost , y				bsint (0 t		2	).

Данные равенства являются параметрическими уравнениями эллипса, так как эллипс получается из окружности радиуса а сжатием ее в а/b раз вдоль оси Оу. Из примера 1 следует, что параметрическими уравнениями

окружности x2	y 2	a2	являются уравнения	x a cost ,
y a sint ( 0 t	2	).	Итак, параметрические	уравнения

эллипса получаются из параметрических уравнений окружности умножением правой части уравнения для

ординаты

на b/а

и имеют вид:

a cost ,

bsint

( 0 t

) .

Можно

поступить

проще.

Исключая

из

этих

уравнений параметр

t (разрешая их относительно

cost и

sint ,

возводя полученные равенства в квадрат и складывая),

получаем

x 2

y 2

cos2 t sin2 t

или

a 2

уравнение эллипса.

Параметрическое задание функции имеет особо важное значение при изучении движения точки. Если точка движется на плоскости, то ее координаты х, у являются функциями времени t. Задав эти функции x (t) , y (t) , мы

полностью определим движение точки. Для каждого

промежутка		времени, в	котором	функция	(t) строго
монотонна,		можно, как	и раньше,	определить	функцию
y	(Ф(x)) , графиком которой является кривая, описываемая
			221

за этот промежуток времени движущейся точкой. В последнем примере функции описывали движение точки по эллипсу.

2.Дифференцирование функции, заданной

параметрически. Предположим теперь, что функции x				(t)
и	y	(t) имеют производные, причем	(t)	0 на

некотором промежутке. Тогда производная функции, заданной

параметрически,

выражается формулой

y (x)

(t)

(9.8)

t Ф(x)

(t)

Пример 1.

Найти y (x) ,

если

x R cost , y

Rsint

(

0 t

Решение. Т. к. в нашем случае

Ф(x)

arccos(x R) ,

то

по формуле (9.8) получаем

y (x)

R cos t

cos t

R sin t

t arccos x R

cos

arccos(x R)

R) .

1 x 2 R 2

R 2

x 2

Пусть существуют вторые производные функций

(t)

(t) в некоторой точке t. Тогда можно вычислить вторую

производную функции, заданной параметрически.

Заметим,

что функция

y (x)

(t)

в свою

очередь,

задана

(t)

(x)

' (t)

параметрически уравнениями

(t) и

(t) .

'(t)

Следовательно,

y (x)

(t) (t)

(9.9)

(t) 3

(x)

222

Аналогично можно получить производную от у по x

любого порядка.

Пример 2.

Найти

y (x) ,

если x

cost ,

sint (

Решение.

y (t)

c o st ,

y (t)

s i nt

x (t)

s i nt ,

x (t)

cost , поэтому по формуле (9.9) найдем

y (x)

(

sin t)(

sin t)

(

cost) cost

(

sin t)3

arccosx

sin2 t

cos2 t

(

sin t)3

arccosx

sin3 t

arccosx

x2 )3 2

Задачи к п. 9

Найти производные следующих функций:

1. y 6 2x

x4 . 2. y

. 3. y x 2 3 x5

3 x2

2sin x

3tgx.

10. y

13. y

16. y

20. y

sin x

cosx

tg x

11.

arctg

12.

sin x

cosx

cos2 (sin

arctg(x

x2 ).

14.

sin

x .

15.

e x 2

sin

xe 2 . 17.

18.

2 ln x .

19. y

32 x .

21. y

lnx lgx

ln a loga x.

22.

y log2 ln 2x.

223

Используя предварительное логарифмирование, найти производные следующих функций:

23.	y		(x		3)2 (2x			1)		. 24. y							3	(x		2)(x 1)2		.	25. y		xsin x .
23.	y					1)3				. 24. y							3					.	25. y		xsin x .
				(x		1)3														x5
			x2 x .												3								1
															3		x .						1
26.	y						27.				y		x				x .			28.	y		(ln x) x .
	Для функций, заданных параметрически, найти yx :
29.	x		2t,			y	3t 2			5t,		t	(				,			).
30.	x		t 3		2,		y		0.5t 2 ,				t				(		,	).
			1							t	2
31.	x		1		,	y				t		.
31.	x	1		t	,	y			t	1		.
		1		t					t	1
32.	x	2		t ,			y 22t ,					t	(				,			).
	Найти производные второго порядка следующих
функций:

33.	y		cos2 x.					34.				y		arctg x2.						35.		y	log2	3 1 x2 .
36.	y		e	x 2 .
	Найти производные второго порядка следующих
функций, заданных параметрически:
37.	x	sect,				y	tg t,				t	(0,				).
37.	x	sect,				y	tg t,				t	(0,		2		).
38.	x	arcsint,					y		ln(1			t 2 ),					t (		1,1).

Написать уравнение касательной и нормали к графику функций y f (x) в данной точке, если:

39.	y	x2		5x	4,		x	1.
							0
40.	y	x3		2x2		4x	3,	x	2.
								0
41.	y		x,		x0	4.
42.	y	tg2x,			x0	0.
									224

43.	В какой точке M0	кривой	y 2 2x3	касательная
перпендикулярна к прямой 4x		3y 2	0?
	Составить уравнение нормали к параболе
44.	Составить уравнение нормали к параболе			y	x 2

в точке пересечения с биссектрисой первого координатного угла.

45. Закон движения материальной точки по прямой имеет

вид x	1	t 4	4t 3 16t 2 .
	4

а) В какие моменты времени точка находится в начале координат?

б) В какие моменты времени направление ее движения совпадает с положительным направлением оси Ох?

в) В какие моменты времени ее ускорение равно нулю? 46. Тело массой 4 движется прямолинейно по закону

x t 2 t 1. Определить кинетическую энергию тела в момент времени t = 5.

47.Радиус шара изменяется со скоростью v. С какой скоростью изменяются объем и площадь поверхности шара?

48.Доказать, что для линейной функции y ax b

приращение y и дифференциал dy совпадают.

49. Найти приращение

и дифференциал dy функции

y x3 , соответствующие значению аргумента

2 и двум

различным значениям аргумента (

x)1

0.1

и (

x)2

0.01.

50. Найти приращение

и дифференциал dS площади S

квадрата,

соответствующие

приращению

стороны

помощью

рисунка

геометрически

истолковать

разность

dS .

Найти дифференциал указанных функций при

произвольных значениях аргумента

х и при произвольном его

приращении

x dx :

51. x

a2 arcsin

52.

sin x

xcosx

53.

xarctgx

ln 1 x2 .

54.

xln x x

225

55.

Вычислить приближенно:

а)

arcsin0.05;

б)

arctg1.04;

в) ln1.2.

56.

Обосновать

приближенную

формулу

3 x

и вычислить по этой формуле

3 25.

33 x2

57.

Найти

приближенное

значение

функции

f (x)

ex 2

при

1.2 .

Ответы к п. 9

39.

7x + y

3 = 0,

7y + 71 = 0.

40. y

5 = 0,

x + 2 = 0.

41.

x 4y + 4 = 0,

4x + y

18 = 0.

42. y

2x = 0,

x + 2y = 0.

43.

M 0 (1/ 8,

1/16). 44.

0 .

45.

а) t1

б)

в)

(0,4)

(8,

);

4 / 3(3

3),

t2 4 / 3(3

3).

46. 242.

47.

4 r 2v; 8 rv.

49.

(

1.261;

(dy)

1.2;

( y)2

0.120601; (dy)2

0.12. 50.

2x x

( x)2 ;

55.а) 0.05; б) 0.805; в) 0.2. 56. 2.93. 57. 1.2.

226

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1.Шипачев В.С. Высшая математика / В.С. Шипачев.

М.: Наука, 2000.

2.Бугров Я.С. Элементы линейной алгебры и

аналитической геометрии / Я.С. Бугров, С.М. Никольский.

М.: Наука, 1980.

3. Бугров Я.С. Дифференциальное и интегральное исчисление / Я.С. Бугров, С.М. Никольский. М.: Наука,

1980.

4. Ефимов Н.В. Краткий курс аналитической геометрии / Н.В. Ефимов. – М.: Наука, 1976.

5.Пискунов Н.С. Дифференциальное и интегральное исчисления / Н.С. Пискунов. - М.: Наука, 1985. Т.1. 429 с.

6.Шипачев В.С. Сборник задач по высшей математике /

В.С. Шипачев. М.: Наука, 1998.

7. Линейная алгебра и основы математического анализа: сборник задач по математике для втузов / под ред. А.В. Ефимова и Б.П. Демидовича. – М.: Наука, 1981.

8.Клетеник Д.В. Сборник задач по аналитической геометрии / Д.В. Клетеник. – М.: Наука, 1980.

9.Берман Г.Н. Сборник задач по курсу математического анализа / Г.Н. Берман. – М.: Наука, 1989. 416 с.

10.	Каплан И.А. Практические	занятия по высшей
математике / И.А. Каплан. – Харьков: ХГУ, 1973. Ч. 1, 2.
11.	Данко П.Е. Высшая математика в упражнениях и
задачах / П.Е. Данко, А.Г. Попов,		Т.Я. Кожевникова. - М.:
Высш. шк., 1986. Ч. 1. – 304 c.

227

<<< < Предыдущая 1 2 34 / 54 5 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
15.11.20225.62 Mб13471.pdf
#
15.11.20225.66 Mб13474.pdf
#
15.11.20225.76 Mб13478.pdf
#
15.11.20225.76 Mб23479.pdf
#
15.11.20225.79 Mб23483.pdf
#
15.11.20225.8 Mб33484.pdf
#
15.11.20225.83 Mб43487.pdf
#
15.11.20225.83 Mб33489.pdf
#
15.11.20225.85 Mб13490.pdf
#
15.11.20225.85 Mб573491.pdf
#
15.11.20225.85 Mб403492.pdf