Рассмотрим снова систему уравнений

Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Воронежский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

3484.pdf

Скачиваний:

Добавлен:

15.11.2022

Размер:

5.8 Mб

Скачать

☆

<<< < Предыдущая 1 23 / 53 4 5 > Следующая >>>

система (1.8) либо не имеет решения, либо имеет бесконечное множество решений.

Если h1 h2 h3 0 , то система (1.8) называется

однородной.

З а м е ч а н и е 3. Однородная система всегда имеет нулевое решение x y z 0 , единственным это решение

будет только тогда, когда главный определитель системы отличен от нуля.

1.4. Матричная запись системы линейных уравнений. Понятие обратной матрицы

нулевым и обозначается 0

или просто 0.

Расстояние между началом и концом вектора называется

его длиной и обозначается

a1x		b1 y	c1z	h1,
a2 x		b2 y	c2 z	h2 ,	(1.10)
a3x		b3 y	c3z	h3.
Введем следующие обозначения:
a1	b1	c1	x	h1
A a2	b2	c2 , X	y , H	h2 .	(1.11)
a3	b3	c3	z	h3

Тогда, используя правило умножения матриц, систему (1.10) можно записать в эквивалентном матричном виде

AX = Н,	(1.12)
где А – заданная матрица, Н –	заданный вектор-столбец,

Х – неизвестный вектор-столбец. Решением уравнения (1.12) является такой вектор-столбец Х, который обращает уравнение (1.12) в тождество.

Пусть определитель матрицы А отличен от нуля. Тогда, как установлено в п. 1.3, система (1.10) и, следовательно, система (1.12) имеют единственное решение, которое находится по формулам Крамера. Дадим теперь другую форму записи решения уравнения (1.12). Для этого введем понятие обратной матрицы.

Определение. Обратной для матрицы А называется

такая матрица (обозначение A 1 ), которая удовлетворяет условиям

A 1	A	A A 1				E ,		(1.13)
где Е – единичная матрица.
Если определитель			0,		то обратной для матрицы А
является матрица:
A1 /		A2 /				A3 /
A 1 B /		B	2	/		B /	,	(1.14)
1						3
C1 /		C2 /				C3 /
где, как и ранее, Ai, Bi,		Ci – алгебраические						дополнения
соответственно элементов		ai , bi , ci				(i = 1, 2, 3).
Таким образом,	обратной				для		матрицы	А является
матрица A 1 , определяемая формулой (1.14). А из равенства
(1.13) следует, что матрица А –					обратная для матрицы A 1 .
Поэтому матрицы А и	A 1	называются взаимнообратными.
З а м е ч а н и е.	Если определитель матрицы А равен

нулю ( = 0), то обратная матрица не существует. Воспользуемся обратной матрицей для решения

уравнения (1.12). Умножая уравнение (1.12) слева на матрицу

A 1 , получаем
A 1 AX		A 1H.	(1.15)
Так как A 1 A	E , а	EX	X , то из (1.15) следует
равенство
X	A 1H .		(1.16)

Итак, если 0, то решение уравнения (1.12), а значит и системы (1.10), можно записать в матричном виде (1.16). Это решение, конечно, то же самое, что было получено в п. 1.3 по формулам Крамера. Этот факт, вытекающий из

единственности решения системы (1.10) при 0, можно непосредственно проверить, если подставить в формулу (1.16) выражение (1.14) для

A 1 и выражения (1.11) для Х и Н.

x	A1 /	A2 /	A3 /	h1
Имеем y	B1 /	B2 /	B3 /	h2	, откуда
z	C1 /	C2 /	C3 /	h3

	x h1 A1		h2 A2	h3 A3 /				x / ,
	y h1B1		h2 B2		h3B3 /			y / ,
	z h1C1		h2C2		h3C3 /			z / ,
т. е. получили формулы Крамера.
	Пример.		Решить				систему		уравнений
x	2 y	z	1,
2x	y	z	1,
x	3y	z	2.
				1		2	1	1
	Решение.	Имеем A		2		1	1 , H	1 .
				1		3	1	2
	Определитель матрицы А равен 1							0.	Следовательно,
матрица А имеет обратную. По формуле (1.14)									находим
					2	1	1
			A 1		1	0	1 .

5 1 3

Используя матрицу A 1 , по формуле (1.16) получаем

x	2	1	1	1	1
y	1	0	1	1	1 , откуда x	1, y 1, z 0.
z	5	1	3	2	0

1.5. Метод Гаусса

Метод Гаусса основан на приведении системы уравнений к треугольному виду. Это достигается последовательным исключением неизвестных из уравнений системы: сначала с помощью одного из уравнений исключается x из всех остальных уравнений, а затем с помощью какого-либо из

оставшихся уравнений исключается	y из всех оставшихся,
кроме двух использованных и так	далее.	Для удобства
исходная система уравнений и полученные из		нее системы

записываются в виде матриц, элементы которых являются коэффициентами при неизвестных, а последний столбец состоит из свободных членов.

Пример. Доказать совместность системы

x	4 y	2z	3,
3x	y	z	5,
3x	5y	6z	9

линейных уравнений и решить ее методом Гаусса.

Решение. Умножим первую строку матрицы на

3 и прибавим ее ко второй и третьей строкам матрицы. Получим

1	4	2	3	1	4	2	3
3	1	1	5	0	13	7	14 .
3	5	6	9	0	7	0	0
				17

Особенность данной системы уравнений заключается в том, что после проделанных операций из третьего уравнения исключились сразу две неизвестные y и z.

Перепишем полученную систему в явном виде

		x	4 y	2z	3,
			13y	7z	14,
			7 y		0.
Из последнего уравнения найдем y					0	и подставим во
второе уравнение. Получим z				2 . Найденные значения y			и z
подставим в первое уравнение и определим x						1.
К треугольному виду приводятся только системы
уравнений,	у	которых		матрица,	составленная		из

коэффициентов, невырожденная. Метод Гаусса позволяет сделать и заключение о совместности системы: если полученная треугольная система имеет решение, то исходная система уравнений также имеет решение. В данном случае система совместна и ее решение (1;0;2).

1.6. Ранг матрицы. Теорема Кронекера-Капелли

Рассмотрим матрицу A размера m				n
	a11	a12	a13	a1n
	a21	a22	a23	a2n
A	a31	a32	a33	a3n .

	am1	am2	am3 amn
Выделим в ней k	строк и k		столбцов ( k		min(m;n) ). Из элемен-

тов, стоящих на пересечении выделенных строк и столбцов, составим определитель k -го порядка. Все такие определители называются минорами этой матрицы.

Наибольший из порядков миноров данной матрицы, отличных от нуля, называется рангом матрицы. Обозначается r , r( A) или rang A .

Минор, порядок которого определяет ранг матрицы, называется базисным. У матрицы может быть несколько базисных миноров.

Пример 1. Найти ранг матрицы
	2		0	4	0
A	3		0	6	0 .
	1		0	3	0
Решение. Все миноры 3-го порядка равны нулю. Есть минор 2-го
порядка, отличный от нуля			6	15	0 .	Значит, r(A)	2 .
		3	6
		1	3
		1	3
Базисный минор стоит на пересечении 2 и 3 строки с 1 и 3 столбцами.
Пусть дана произвольная система				m линейных уравнений с			n
неизвестными
a11 x1	a12 x2			a1n xn		b1,
a21 x1	a22 x2			a2n xn		b2 ,
.......... .......... .......... .......... .......... ..
am1x1	am2 x2			amn xn		bm .

Определение. Матрица A , составленная из коэффициентов при неизвестных, называется основной.

Матрица A , получающаяся из основной присоединением столбца свободных членов, называется расширенной матрицей системы.

Исчерпывающий ответ на вопрос о совместности этой системы дает

теорема Кронекера-Капелли.

Теорема 1. Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг расширенной матрицы системы равен рангу основной матрицы.

Правила практического разыскания всех решений совместной системы линейных уравнений вытекают из следующих теорем.

Теорема 2. Если ранг совместной системы равен числу неизвестных, то система имеет единственное решение.

Теорема 3. Если ранг совместной системы меньше числа неизвестных, то система имеет бесчисленное множество решений.

Правило решения произвольной системы линейных уравнений.


1.	Найти ранги	основной и расширенной матриц		системы. Если

r( A)	r( A) , то система несовместна.

2. Если r( A) r( A) r , система совместна. Найти какой-либо ба-
зисный минор порядка			r (напоминание: минор, порядок	которого опре-
деляет	ранг матрицы,	называется базисным). Взять r		уравнений, из

коэффициентов которых составлен базисный минор (остальные уравнения отбросить). Неизвестные, коэффициенты которых входят в базисный минор, называют главными и оставляют слева, а остальные n r неизвестных называют свободными и переносят в правые части уравнений.

3.Найти выражения главных неизвестных через свободные. Получено общее решение системы.

4.Придавая свободным неизвестным произвольные значения, получим соответствующие значения главных неизвестных. Таким образом можно найти частные решения исходной системы уравнений.

Пример 2. Исследовать на совместность систему

Решение.

, r(A)

r( A) 2

0 .

3 3

2 ,

Таким образом, r( A)

r( A) , следовательно, система несовместна.

Пример 3. Решить систему

2x2

3x4

Решение. r( A)

r( A)

2 . Берем два первых уравнения:

2x2

x4 1,

или

1 x1

2x2 ,

2x2

1 x1 2x2.

Найдем

определитель

этой

системы

и вспомогательные

определители

			1		1	2 0 ,						1		x1	2x2		1		2x1		4x2 ,
			1		1	2 0 ,			1			1		x1	2x2		1		2x1		4x2 ,
			1		1							1		x1	2x2		1
									1	x1			2x2		2 .
								1	1	x1			2x2
					2			1	1	x1			2x2
					2

	Применяя формулы Крамера, получим													x3		x1	2x2 , x4				1 —
общее решение. Положив, например,											x1		0 ,		x2	0 ,	получаем одно из
частных решений:					x1	0 ,		x2	0 ,	x3		0 , x4			1.
								Задачи к п. 1
	Вычислить:
1. 3А		2В,		если А			2		1	1	,		В		2	1	0 .
							0		1	4					3	2	2
2.	3	2		3 4 .			3.		2	3			9		6 .
	5	4		2	5				4	6			6		4
	1	3		2	2	5	6			5	8			4	3		2	5
4. 3		4 1			1 2 5 . 5. 6 9									5	4		1 3 .
	2	5		3	1	3	2			4	7			3	9		6	5
						6												3
	5	0		2	3	6												1
	5	0		2	3	2 . 7. 4 0												1
6.	4 1 5 3					2 . 7. 4 0								2 3 1				1 .
	3	1		1	2	7												5
	3	1		1	2	4												5
						4												2
																		2
		0		0	1		1		1
		1		1	2		1		1	4 .
	8.	1		1	2	2			2	4 .
		2		2	3	1			1	1
		3		3	4	1			1
		3		3	4
	9.	Вычислить определитель второго порядка:																		4	.
	9.	Вычислить определитель второго порядка:																	1	4	.
																			5	2
										21

10. Решить уравнение:							x	x	1	0.
10. Решить уравнение:							4	x	1	0.
							4	x	1
Вычислить определители третьего порядка:
		2	`3					3	4			5
	1	2	`3					3	4			5
11.	4	5	6	.	12.			8	7			2	.
	7	8	9					2	1	8
Решить уравнения:
		3	x		x						x			x	1	x	2
		3	x		x						x			x	1	x	2
13.		2	1		3	0.			14.	x		3		x	4	x	5	0.
	x	10	1		1					x		6		x	7	x	8
Решить неравенства:
		2 1									2		x	2		1
	3	2 1									2		x	2		1
15.	1	x	2		0.				16.		1			1		2	0.
	1 2		1								5			3		x

Решить системы уравнений с помощью правила Крамера:

	7x	2 y	3z	15,			2x	y		5,
17.	5x	3y	2z	15,		18.	x	3z		16,
	10x	11y	5z	36.			5 y	z		10.
	x	y	2z	6,		x	y		z	36,
19.	2x	3y	7z	16,	20.	x	z		y	13,
	5x	2 y	z	16.		y	z		x	7.
	Найти обратные для следующих матриц:
	1	2 .		3	4 .			2	5	7
21.	1	2 .	22.	3	4 .		23.	6	3	4 .
	3	4		5	7			5	2	3
								5	2	3

	3	4	5		2		7	3		1	2	2
24.	2	3	1 .		25. 3		9	4 .	26.	2	1	2 .
	3	5	1		1		5	3		2	2	1
	Решить матричные уравнения:
27.	1	2	X	3	5 .
	3	4		5	9
	1	2	3		1		3	0
28.	3	2	4	X	10		2	7 .
	2	1	0		10		7	8
		5	3	1	8		3	0
29.	X	1	3	2	5		9	0 .
		5	2	1	2		15	0
	Решить системы уравнений матричным методом:
	x		2 y		3z		0,
30.	2x		y		4z		5,
	3x		y		z		2.
	3x	3y		2z		2,
31.	4x	5 y		2z		1,
	5x	6 y		4z		3.
	3x	2 y		4z			8,
32.	2x	4 y		5z		11,
	4x	3y		2z			1.
	Найти все решения следующих систем:
	x		2 y		4z		1,
33.	2x		y		5z		1,
	x		y		z		2.
							23

	2x		y	z		2,
34.	x	2 y		3z		1,
	x	3y		2z		3.
	3x		y	2z		5,
35.	2x		y	z		2,
	4x		2 y	2z		3.
	2x		y	z		0,
36.	x	2 y		z		0,
	2x		y	3z		0.
	x		y	z		0,
37.	x		4 y	2z		0,
	3x		7 y	3z		0.
	x	y		z	a,
38.	x	y		z	b,
	x	y		z	c.
	Решить		системы		уравнений		или		доказать их
несовместность.
	x1	2x2	3x3	4x4	4,		2x1	x2	x3	4,
39.		x2	x3	x4	3,	40.	x1	3x2	x3	5,
39.	x1	3x2		3x4	1,	40.	x1	x2	5x3	7,
	x1	3x2		3x4	1,		x1	x2	5x3	7,
		7x2	3x3	x4	3.		2x1	3x2	3x3	14.
	x1	2x2	x3	x4 1,
41.	x1	2x2	x3	x4	1,
	x1	2x2	x3	5x4	5.

Ответы к п. 1

1.	2 5						3 .			2.	5 2 .					3.	0 0 .
	6				7		8				7	0					0	0
	1				5	5			11	22		29			56							5
	1				5	5			11	22		29			56							15 .
4.	3			10		0	. 5.		9	27		32 . 6.			69 . 7.			31 . 8.				15 .
	2				9	7			13	17		26			17							25
	2				9	7			13	17		26			17							35
																						35

9.	18.				10.	x1		4,	x2		1.	11.		0.	12.		0.	13.	4					22.
14.	(				,+	).	15.	(4,+		).	16.		(	6,	4). 17.			x = 2,				y =		1,
z = 1.					18.	x = 1,			y = 3,		z = 5.			19.		x = 3,		y = 1,				z =		1.
20.		x = 24.5,					y = 21.5,			z = 10.
				2		1 .				7		4 .					1		1			1
21.				2		1 .		22.		7		4 .			23.		38		41			34 .
	3/ 2					1/ 2				5		3					27		29			24
																	27		29			24
	8 29					11				7 / 3 2			1/ 3				1/ 9 2 / 9					2 / 9
24.	5				18		7 .	25.		5 / 3		1	1/ 3 .			26. 2 / 9 1/ 9						2 / 9 .
	1				3 1					2	1			1			2 / 9		2 / 9 1/ 9
	1				1 . 28.			6	4	5			1	2		3				1
27.	1							2	1	2 . 29.			4	5		6 .	30.	x		1	,		y = 2,
27.								2	1	2 . 29.			4	5		6 .	30.	x			,		y = 2,
	2				3			3	3	3			7	8		9			2
								3	3	3			7	8		9
z =		3	.	31.		x = 1,		y =		1,	z = 1.			32.		x = 2,		y = 3,					z = 1.
z =	2		.	31.		x = 1,		y =		1,	z = 1.			32.		x = 2,		y = 3,					z = 1.
	2
33.		Система					имеет		бесконечно				много			решений			x			2z		1 ,
y		z		1,		z	задается произвольно.								34.		Система не имеет
решений. 35. Система не имеет решений.																	36.	x		y			z	0 .
37.			Система имеет бесконечно											много решений								x		2t ,
y			3t ,			z	5t ,		t	задается произвольно.								38.		x			b	c	,
y			3t ,			z	5t ,		t	задается произвольно.								38.		x		2			,
																						2

y	a	b	,	y	a c	. 39.	( 8,3 x4 ,6 x4 , x4 ) . 40.	(1,2, 2) . 41.
	2				2

(x1, x2 ,		x1		2x2 ,1) .

2.ВЕКТОРНАЯ АЛГЕБРА

2.1.Скалярные и векторные величины

Многие физические величины полностью определяются

заданием некоторого числа. Это, например, объем, масса, плотность, температура тела и др. Такие величины называются скалярными. В связи с этим числа иногда называют скалярами. Но есть и такие величины, которые определяются заданием не только числа, но и некоторого направления. Например, при движении тела следует указать не только скорость, с которой движется тело, но и направление движения. Точно так же, изучая действие какой-либо силы, необходимо указать не только значение этой силы, но и направление ее действия. Такие величины называются векторными. Для их описания было введено понятие вектора, оказавшееся полезным для математики.

Любая упорядоченная пара точек А и В пространства определяет направленный отрезок, т. е. отрезок вместе с заданным на нем направлением. Если точка А первая, то ее называют началом направленного отрезка, а точку В – его концом. Направлением отрезка считают направление от начала к концу.

Определение 1. Направленный отрезок называется вектором.

Будем обозначать вектор символом AB , причем первая буква означает начало вектора, а вторая – его конец. Вектор также обозначают и одной буквой с черточкой наверху, например a . Направление вектора на рисунке указывают стрелкой (рис. 1).

А В

Рис. 1

Вектор, у которого начало и конец совпадают, называется

Векторы a и b называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Коллинеарные векторы могут быть направлены одинаково или противоположно. Нулевой вектор будем считать направленным одинаково с любым вектором; длина его равна нулю, т. е.

0 0 .

Рис. 2

Рис. 3

Теперь можно сформулировать важное понятие равенства двух векторов.

Определение 2. Векторы a и b называются равными

(a b ) , если они коллинеарны, одинаково направлены и их

длины равны.

На рис. 2 только справа равные векторы. Из определения равенства векторов следует, что если данный вектор перенести параллельно самому себе, то получится вектор, равный данному. В связи с этим векторы в аналитической геометрии называют свободными.

2.2.Проекция

1.Проекция вектора на ось. Пусть в пространстве

заданы ось и и некоторый вектор AB . Проведем через точки А и В плоскости, перпендикулярные оси и. Обозначим через А' и В' точки пересечения этих плоскостей с осью (рис. 3).

Определение.

Проекцией вектора

на

ось

называется величина А'В' направленного отрезка

на оси

A B

и. Напомним, что

А'В' =

, если

совпадает с

A B

направлением оси

и, А'В' =

если направление

A B

противоположно направлению оси и.

Обозначается проекция вектора

на ось

так:

при

AB .

Теорема 1. Проекция вектора AB на ось и

равна длине

вектора AB ,

умноженной на косинус угла между вектором

и осью

и, т. е.

при AB =

cos

где

угол между вектором AB и осью и.

З а м е ч а н и е 1. Равные векторы имеют равные

проекции на одну и ту же ось.

2. Проекции

вектора

на оси

координат. Пусть в

пространстве заданы прямоугольная система координат Oxyz и произвольный вектор AB . Пусть, далее, X =прx AB , Y= прy AB ,

Z = прz AB . Проекции X, Y, Z

вектора AB на оси координат

X ;Y; Z .

называют его координатами. При этом пишут AB =

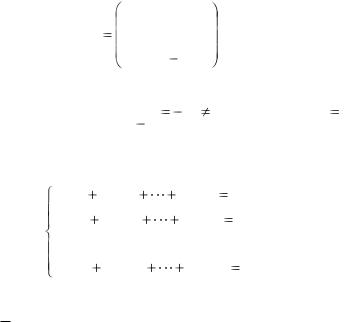
Теорема

Каковы

бы ни были две точки

A(x1; y1; z1) и

B (x2; y2 ; z2 ) ,

координаты

вектора

определяются

следующими

формулами:

x1,

Y y2 y1 ,

Z z2

z1 .

З а м е ч а н и е 2. Если вектор			AB	выходит из начала

координат, то координаты	вектора	AB		равны координатам
точки B.
3. Направляющие косинусы вектора. Пусть дан
произвольный вектор a	X ; Y; Z ;		будем считать, что a
выходит из начала координат О		и не лежит ни в одной

координатной плоскости. Проведем через точку А плоскости, перпендикулярные осям. Вместе с координатными плоскостями они образуют прямоугольный параллелепипед, диагональю которого служит отрезок ОА (рис. 4).

Рис. 4

Из элементарной геометрии известно, что квадрат длины диагонали прямоугольного параллелепипеда равен сумме квадратов длин трех его измерений. Следовательно,

	a	X 2	Y 2 Z 2 .	(2.1)

Формула (2.1) выражает длину произвольного вектора
через его координаты.
Обозначим через ,		,	углы между вектором	a и
осями координат. Очевидно,
		29

cos

X 2

Y 2

Z 2

cos

X 2

Y 2

Z 2

cos

X 2

Y 2

Z 2

Числа cos , cos , cos

называются направляющими

косинусами вектора

a . Возводя в квадрат левую и правую

части каждого из этих равенств

суммируя

полученные

результаты, имеем

cos2

т. е. сумма

квадратов направляющих косинусов любого вектора равна единице.

В заключение пункта рассмотрим задачу. Пусть даны две произвольные точки M1(x1; y1; z1) и M 2 (x2; y2 ; z2 ) . Найдем расстояние d между ними. Используя теорему 2 и формулу

(2.1),	сразу	получаем	искомый	результат
______
M1M 2	{x2 x1, y2	y1, z2 z1},	а так как d – длина вектора

M1M 2 , то

	______
	______				x )2			y )2			z )2 .
d	M M	2	(x	2	x )2	( y	2	y )2	(z	2	z )2 .
	1	2		2	1		2	1		2	1

2.3. Линейные операции над векторами и их основные свойства

Линейными операциями над векторами называются операции сложения, вычитания векторов и умножения векторов на числа.

1. Сложение двух векторов. Пусть даны два вектора a и

b . Суммой a + b называется вектор, который идет из

начала вектора a в конец вектора b при условии, что вектор b приложен к концу вектора a (рис. 5, а).

З а м е ч а н и е 1. Действие вычитания векторов обратно

действию сложения, т. е. разностью			векторов
	b	a
называется вектор, который в сумме с вектором		a	дает вектор

b(рис. 5, б).

За м е ч а н и е 2. Определив сумму двух векторов, можно найти сумму любого числа данных векторов. Пусть, например,

даны три вектора a ,

b ,

Сложив

и b , получим вектор a

+ b . Прибавив к нему теперь вектор

, получим вектор

a + b +

2. Произведение вектора на число.

Пусть даны вектор

0 и число

0 . Произведением

называется вектор,

который коллинеарен вектору a , имеет длину,

равную

и направление такое же, как и вектор

a ,

если

0 ,

противоположное, если

0 (рис. 6).

Геометрический

смысл

операции

умножения

вектора

0 на число

0 можно выразить следующим образом:

1 , то при умножении вектора

если

на число

вектор a

”растягивается” в

раз, а если

1 – “сжимается”

раз. При

вектор

изменяет

направление

на

противоположное. На рис. 6 изображен случай

1 .

Если

или

0 , то произведение

a считается

равным нулевому вектору.

З а м е ч а н и е

3. Используя определение умножения

вектора на число, нетрудно доказать, что если векторы

a и

b ,

коллинеарны и a

0 , то существует (и притом только одно)

число

такое, что

a .

(

a (

а)

б)

Рис. 5

Рис. 6

3. Основные свойства линейных операций.

1о. a

(переместительное свойство сложения).

2о.

b )

a (b c ) (сочетательное

свойство

сложения).

Рассмотрим еще три свойства линейных операций, два из

которых

относятся

одновременно к сложению векторов и

умножению вектора на число. Пусть

– произвольные

числа, a и

b – любые векторы. Тогда:

3о.

(

(сочетательное свойство умножения);

4о.

(

(распределительное

свойство

относительно суммы чисел);

5о.

b )

(распределительное

свойство

относительно суммы векторов).

З а м е ч а н и е 4. Сформулированные свойства линейных операций имеют фундаментальное значение, так как дают

возможность	производить	над	векторами	обычные
алгебраические действия. Например, в силу свойств				4о и

5о можно выполнять умножение скалярного многочлена на векторный многочлен «почленно».

4. Теоремы о проекциях векторов.

Теорема 1. Проекция суммы двух векторов на ось равна

сумме	их	проекций	на эту ось (рис. 7), т.е.
пр u (a1	a2 )	пр u a1	пр u a2 .
			32

Теорему можно обобщить на случай любого числа слагаемых.

Теорема 2. При умножении вектора a на число его проекция на ось также умножается на это число (рис. 8), т. е.

пр u	a	пр u a
	С л е д с т в и е			1.	Из теоремы	1	вытекает, что если
			и					то
a	X1;Y1; Z1				b X 2 ;Y2 ; Z 2 ,
a b	X1	X 2 ; Y1 Y2 ; Z1			Z 2 .
	С л е д с т в и е			2.	Из теоремы	2	вытекает, что если
a	X ;Y; Z , то		a	X ;	Y; Z для любого числа .

Рис. 8

Рис. 7

Отсюда легко выводится условие коллинеарности двух

векторов в координатах. В самом деле,

равенство

равносильно равенствам X 2 X1,

Y1,

или

X 2

т. е. векторы

a и

коллинеарны в

том и только в том случае, когда их координаты пропорциональны.

5. Разложение вектора по базису. Пусть векторы i , j, k

единичные векторы осей координат,

т.

е.

каждый из них одинаково

направлен с соответствующей осью

координат. Тройка векторов i ,

j, k

называется базисом.

Теорема 3. Любой вектор

может

быть

единственным

образом разложен по базису

i , j, k ,

т.

е.

представлен в виде

k , где

- некоторые

числа.

Пример. Даны три вектора a

1;2;3

, b

2;3;1

3;1;2

. Найти разложение вектора d

2;1;3

по

базису

a , b ,

Решение. Найдем координаты вектора

базисе a ,

b ,

Обозначим

эти

координаты

x, y, z . Тогда имеем

равенство

zc , которое в

координатой

форме

примет вид системы уравнений относительно

неизвестных

x, y, z

2 y

Решим

систему

уравнений

методом

Крамера.

Определитель этой системы

18 .

Вспомогательные определители:

1 3 1

12 ,

2 1 1

6 ,

2 3 1

12 .

Решение системы уравнений получим по формулам Крамера

						x			x		2	,			y			y			1	,		z			z		2	.
						x				3		,			y				3			,		z					3	.

		Итак,					вектор d							в базисе					a ,			b ,				имеет координаты
		Итак,					вектор d							в базисе					a ,			b ,			c	имеет координаты
2	;		1	;	2			и		может						быть				представлен								в виде
3	;	3		;	3			и		может						быть				представлен								в виде
3		3			3
																2	a		1			2	c .
													d			2			1	b		2
													d							b
															3				3			3

2.4.Скалярное произведение векторов

1.Определение и основные свойства скалярного произведения.

Определение. Скалярным произведением двух ненулевых

векторов a и b называется число (скаляр), равное произведению длин этих векторов на косинус угла между ними. Если хотя бы один из векторов нулевой, то угол не определен и

скалярное

произведение

по

определению

полагают равным

нулю.

Скалярное произведение векторов a

b обозначают a

b . Итак, a

cos

где

угол между векторами

a и b (рис. 9).

Так как

cos

пр

cos

пр a b , то можно

записать

a b

пр

пр a b .

Типичным примером скалярного произведения в физике

является формула работы

где вектор a

cos

сила, точка приложения

которой перемещается из начала в

конец вектора

b (рис. 10).

Рис. 10

Рис. 9

Рассмотрим некоторые свойства скалярного произведения.

1о.				(свойство	перестановочности
	a b	b a
сомножителей).
2о.				(свойство	сочетательности
	( a ) b		(a b )

относительно умножения на число).

З а м е ч а н и е 1. Из свойств 1о и 2о следует, что

( a ) ( b ) ( )(a b ) .

3о. a (b c ) a b a c (свойство распределительности

относительно суммы векторов).

З а м е ч а н и е 2. Данное свойство дает право при скалярном умножении векторных многочленов выполнять действия почленно. В силу свойства 1о можно при этом не заботиться о порядке сомножителей, а свойство 2о позволяет (см. замечание 1) объединить числовые коэффициенты векторных сомножителей. Например,

(2a 5b ) (3c

4d ) (2a 5b ) (3c ) (2a 5b ) (4d )

(2a ) (3c )

(5b ) (3c ) (2a ) (4d ) (5b ) (4d )

6a c 15b c 8a d 20b d . 4о. a a a 2 .

Скалярное произведение a a называется скалярным квадратом вектора a и обозначается a 2 .

5о. a

0, если

b , и, обратно, a

b , если

a b

и a

0 ,

0 .

З а м е ч а н и е

Из свойств 4о

и 5о для базисных

векторов

непосредственно

получаем

следующие

i , j, k

равенства:

0 .

i j

i k

j i

j k

k i

k j

2. Выражение скалярного произведения через

координаты векторов.

Если векторы

заданы

своими

Теорема.

координатами: a X1;Y1; Z1

то

их

X 2 ;Y2 ; Z2

скалярное

произведение

определяется

формулой

a b X1 X 2

Y1Y2

Z1Z 2 .

Из теоремы вытекают два важных следствия.

С л е д с т в и е 1. Необходимым

достаточным

условием

перпендикулярности

векторов

X1;Y1; Z1

X 2 ;Y2 ; Z2

является равенство X1 X 2

Y1Y2

Z1Z2

С л

д с

Угол

между

векторами

X1;Y1; Z1

определяется равенством

X 2 ;Y2 ; Z 2

cos

X1 X 2

Y1Y2

Z1Z2

(2.2)

Z 2

X 2

Y 2

Z 2

Пример. Даны три точки А (1;1;1), В (2;2;1) и

С (2;1;2).

Найти угол

BAC .

Решение.

Применяя

теорему

(п. 2.2), найдем

1;1;0 ,

AC 1;0;1 . Отсюда на основании формулы (2.2)

получаем

cos

1 1

1 0

0 1

Следовательно, = 60 .

2.5.Векторное произведение

1. Определение векторного произведения. Векторы a , b и c называются компланарными, если они лежат в

одной плоскости или в параллельных плоскостях.

Тройка векторов называется упорядоченной, если указано, какой из них считается первым, какой вторым и какой третьим.

Например, в записи (a;b ; c ) вектор a считается первым, b

вторым, c третьим; в записи (b ; c; a ) вектор b

первым, c вторым, a третьим.

Упорядоченная тройка некомпланарных векторов называется правой, если после приведения их к общему началу из конца третьего вектора кратчайший поворот от первого ко второму виден совершающимся против часовой стрелки. В противном случае тройка называется левой.

Определение. Векторным произведением вектора a на

вектор b называется вектор a b , который определяется тремя условиями:

1) длина вектора a b равна a b sin , где - угол

между векторами a и b ;

2) вектор a b перпендикулярен каждому из векторов

aи b ;

3)векторы a , b , a b образуют правую тройку векторов (рис. 11).

Заметим, что условия 2) и 3) относятся к случаю, когда

0, т. е. вектор a

0 .

Если же

sin

(т.е. либо, по крайней мере, один из векторов a

и b нулевой,

либо sin

0), то векторное произведение a b

определяется

только условием 1): в этом случае

b 0 .

Понятие векторного произведения имеет свой источник в

механике.

Пусть в точке М

твердого тела приложена сила

F MK и О – некоторая точка пространства. Как известно из

механики, моментом силы F относительно точки О (точка

приложения момента) называется вектор L , который: 1) имеет

длину, равную OM MK sin , где угол между векторами

OM и MK ; 2) перпендикулярен плоскости , проходящей через точки О, М, К; 3) направлен так, что из его конца сила

F представляется вращающей плоскость вокруг точки О против часовой стрелки (рис. 12).

Рис. 11 Рис. 12

2. Основные свойства векторного произведения.

1 . a b 0 , если a и b - коллинеарные векторы.

2 . Длина векторного произведения неколлинеарных

векторов

равна

площади

параллелограмма,

построенного на этих векторах (см. рис. 11).

3 .

(свойство

антиперестановочности

сомножителей).

4 .

(свойство

сочетательности

по

(

a )

b )

отношению к скалярному множителю).

5 .

(свойство

b )

a c

распределительности относительно суммы векторов).

З а м е ч а н и е 1. Данное свойство дает право

при

векторном

умножении

векторных

многочленов

выполнять

действия почленно, а свойство 4

объединить

числовые

коэффициенты векторных сомножителей. Например,

(2a 3b ) (4c 5d ) (2a 3b ) 4c (2a 3b ) 5d

2a 4c 3b 4c 2a 5d 3b 5d

8(a

c )

12(b

c )

10(a

d )

15(b d ) .

Следует, однако, помнить, что порядок сомножителей векторного произведения является существенным и при перестановке сомножителей знак векторного произведения нужно изменить. Например,

(a b c ) (2b 3c ) 2(a 3(b c ) 3(c c ) 2(a b )

2(a b ) (b c ) 3(a c ).

b ) 2(b b ) 2(c b ) 3(a c ) 2(b c ) 3(a c ) 3(b c )

За м е ч а н и е 2. Согласно определению и свойствам 1

и3векторного произведения для базисных векторов i , j, k получаем следующие равенства:

i i 0; i

j k ; i

j i

k ;

j j 0;

j k

i ; k i

j; k

i ; k k

3. Выражение векторного произведения через координаты векторов.

Теорема. Если векторы a

заданы

своими

координатами:

то

a X1;Y1;

Z1 ,

X 2 ;Y2 ; Z 2 ,

векторное

произведение

вектора

на

вектор

определяется формулой

(2.3)

a b

Y1 Z 2

Y2 Z1 ;

Z1 X 2

Z 2 X1 ;

X1 Y2

X 2 Y1 .

Эту формулу с помощью определителей второго порядка

Y1 Z1

;

можно записать в виде

Y2 Z 2

Z 2 X 2

X 2 Y2

с помощью определителя третьего порядка в виде

X 2

Пример. Даны векторы

Найти

2;5;7 ,

1; 2; 4 .

координаты векторного произведения

b .

Решение.

По формуле

(2.3)

находим

5 7

2 4

2 5

7 2

Итак,

1 .

4 1

2.6.Смешанное произведение трех векторов

1.Определение и геометрический смысл смешанного произведения.

Определение. Смешанным произведением трех векторов

a , b , c называется число, равное скалярному произведению

вектора a на векторное произведение векторов b и c , т. е. a (b c ) .

Следующая теорема выражает геометрический смысл смешанного произведения.

Теорема 1. Смешанное произведение a (b c ) равно объему V параллелепипеда, построенного на векторах a , b , c ,

взятому со знаком «+», если тройка

правая, и со

a , b ,

знаком «-», если

тройка

левая. Если

же

a , b ,

компланарны, то a

0 . Другими словами:

c )

если

a, b , c

правая тройка,

c ) =

если

a, b , c

левая

тройка,

0, если a, b , c

компланарны.

Итак, если векторы a , b ,

компланарны,

то a (b

c ) 0 .

Верно и обратное: если

a (b c )

0 , то векторы a , b ,

компланарны. Действительно, если бы векторы

a , b ,

были

некомпланарны,

то

по

теореме 1

смешанное

произведение

0 , что противоречит условию.

a (b

c )

С л е д с т в и е. Из теоремы 1 следует тождество

a (b

c )

(a b )

c ,

(2.4)

т.е. знаки и

в смешанном произведении можно менять

местами.

силу

тождества

(2.4)

смешанное

произведение

можно

обозначить

более

a (b c )

простым символом

a b c .

2. Выражение смешанного произведения через

координаты векторов.

Теорема 2.

Если

векторы

a , b ,

заданы

своими

координатами

c X 3; Y3; Z3 ,

a X1;Y1; Z1 , b X 2 ;Y2 ; Z2 ,

то смешанное произведение a b c

определяется формулой

Z2 X 2

X 2 Y2

a b c =

X 2

Y Z

X 3

Пример. В

пространстве

даны четыре точки:

A(1;1;1),

B (4;4;4), C(3;5;5),

D (2;4;7). Найти объем тетраэдра ABCD.

Решение. Как известно из элементарной геометрии, объем

V тетраэдра

ABCD

равен

одной

шестой

объема

параллелепипеда, построенного на векторах

AB, AC, AD ;

поэтому из теоремы 1 заключаем, что V равен

абсолютной

величины смешанного произведения AB AC AD .

Найдем это

смешанное произведение. Прежде всего определим координаты


векторов AB, AC, AD . Имеем:									AB	3;3;3 ,		AC	2; 4; 4

	AD 1;3;6 . Используя теорему 2, получаем
					3	4 2	3	2 4		3 12 3 8	3 2		18.
				4 4
			AB AC AD = 3	4 4
				3 6		6 1		1	3
		Отсюда V =		1	18 = 3.
		Отсюда V =		6	18 = 3.
				6

Задачи к п. 2

1. Даны точки A(3; 1;2) и B( 1;2;1) . Найти координаты

векторов AB и BA .

2.Определить точку N , с которой совпадает конец

вектора

3; 1;4

если

его начало

совпадает

с точкой

M (1;2;

3) .

Определить

начало

вектора a

2; 3; 1 ,

если его

конец совпадает с точкой (1;

1;2) .

Вычислить

направляющие

косинусы

вектора

;

13 13 13

Вектор

составляет с осями OX

OY углы

120

450 . Какой угол он составляет с осью OY ?

Даны

13,

19 и

24 . Вычислить

Векторы

образуют угол

60 , причем

5 и

8 . Определить

Даны векторы a

. Определить

2;6

2;1;0

координаты следующих векторов:

а)

b ;

б)

3b ;

в)

b .

Найти орт вектора

3 .

10.

Определить

модули суммы

разности

векторов

4 .

3; 5;8

1;1;

11. На плоскости даны два вектора

1;2 .

Найти разложение вектора a

9;4

по базису p ,

q .

12.

Даны три вектора a

3; 1 , b

1; 2

и c

1;7 .

Определить разложение вектора p

b c по базису a , b .

13.

Даны

три

вектора

2;1 ,

1;1; 1

2;1;

3 . Найти разложение вектора c

11;

6;5

по базису

p ,

q и

14. Векторы

образуют угол

; зная, что

3 ,

a 2 ;

)2 ;

4 ,

вычислить:

а) a b ;

б)

в)

) ; д) (3a 2

)2 .

г) (3a 2

) (a 2

a ,

15. Даны векторы

b и

, удовлетворяющие условию

3 ,

4 , вычислить

a + b +

=0. Зная,

что

ca .

b c

Векторы

образуют угол

;

зная,

что

16.

3 ,

вычислить

угол

между

векторами

b .

17.

Даны

точки

A(1;

2;2) ,

B(2;

1;5)

C(0;1;

5) .

2 ;

2 .

Вычислить: а) (2AB

CB)

(2BC

BA) ; б)

в)

18.

Вычислить

работу

силы

при

2 j

перемещении материальной точки из положения

А(

1;2;0)

положение С(2;1;3).

19.

Вычислить

косинус угла,

образованного векторами

3;2;6 .

20.

Даны вершины треугольника A(

1; 2;4) , B(

4; 2;0)

C(3;

2;1) . Определить его внутренний угол при вершине

B .

21.

Найти

вектор

x ,

коллинеарный

вектору

2 j

2k ,

образующий

ортом

острый

угол

15 .

имеющий длину

22.

Найти

вектор

x ,

образующий

со

всеми

тремя

базисными ортами равные острые углы, если

2 3 .

23. Найти координаты вектора

x , коллинеарного вектору

2;1;

и удовлетворяющего условию

24.

Вектор

перпендикулярен векторам

2;3;

1 ,

2;3

удовлетворяет

условию

(2i

k )

6 .

Найти координаты

x .

25.

Вычислить

проекцию

вектора

5;2;5

на

ось

вектора b

2; 1;2 .

26. Даны векторы a

3;4 ,

4;2

1;1;4 .

Вычислить пр

c a .

27.

Даны векторы a

2;1;1 ,

1;5;0

4;4;

2 .

Вычислить пр c (3a

2b ) .

28.

a1, a2

Вычислить:

а)

;

б)

(2a1

a2 ) (a1

2a2 )

;

3a2 ) (3a1

a2 )

в)

(a1

29.

Упростить выражения:

а) i ( j k )

j (i

k ) k (i

j k ) ;

б) (a b c ) c (a b c ) b (b c ) a ;

в) (2a b ) (c a ) (b c ) (a b ) ;

г) 2i ( j k ) 3 j(i k ) 4k (i

j) .

30.

(a,b)

Вычислить

площадь

треугольника, построенного на векторах

3a 2b .

31.

Заданы векторы

{3; 1;2}

{1;2;

1} . Найти

координаты

векторов:

а)

a2 ;

б)

(2a1

a2 )

a2 ;

в) (2a1

a2 ) (2a1

a2 ) .

32.

Вычислить площадь треугольника с

вершинами

A(1;1;1), В(2;3;4)

и С(4;3;2).

33.

В треугольнике с вершинами

А(1; 1;2),

В(5;

6;2) и

С(1;3; 1) найти высоту

34.

Сила F

4 j

приложена к точке А(4;

2;3).

Определить момент этой силы относительно точки О(3;2;

1).

35.

Даны три силы F1

{2;

3},

{3; 2;

F3 { 4;1; 3}, приложенные к точке

А( 1;4; 2). Определить

величину

направляющие

косинусы

момента

равнодействующей этих сил относительно точки О(2;3;

1).

36.

Найти координаты вектора x ,

если известно,

что он

перпендикулярен

векторам

{4;

{0;1;3},

26.

образует с ортом

тупой угол и

37.Найти координаты вектора x , если он

перпендикулярен

векторам

{2;

3;1}

{1,

2,3}, а

также удовлетворяет условию x

10 .

2 j

7k )

38.

Векторы a1, a2 , a3

образуют

правую

тройку,

взаимно

перпендикулярны

Вычислить a1a2a3 .

39.

Вектор

перпендикулярен к векторам a

b ,

угол

между

a и

равен 30 . Зная,

что

6 ,

3 ,

вычислить ab c .

40.

Доказать

тождество:

(a b

c )(a 2b

2c )(4a b 5c ) 0.

41.

Вычислить

объем

тетраэдра

OABC,

если

OA 3i 4 j; OB

3 j k ; OC 2 j 5k .

42.

Установить компланарны ли векторы a , b и

а)

2;3;

1 ,

1;3

1;9;

11 ;

б)

2;1 ,

;

2;1;2

1; 2

в)

1;2

1;2; 3 ,

4;7 .

43.Вычислить объем тетраэдра с вершинами в точках

А(2;-3;5), В(0;2;1), С(-2;-2;3) и D(3;2;4).

44.В тетраэдре с вершинами в точках А(1;1;1), В(2;0;2),

С(2;2;2)				и D (3; 4;-3)						вычислить высоту h									DE	.
	45.			Доказать, что четыре точки														А(1;2;-1),		В(0;1;5), С(-
1;2;1)			и D(2;1;3) лежат в одной плоскости.
											Ответы к п. 2.
							1 ,						3;1 .					N(4;1;1) .		3. (-1;2;3).
1.		AB		4;3;			1 ,		BA			4;	3;1 .		2.			N(4;1;1) .		3. (-1;2;3).
				3						4					12						0
4.	cos					,	cos					,		cos			.	5.	60	или	1 2 0 .
4.	cos				13	,	cos			13		,		cos		13	.	5.	60	или	1 2 0 .
																					5; 3;6 ;
6.	a		b	22 .			7.	a		b			129 ,		a b			7 .	8.	а)	5; 3;6 ;
													47
													47

б) 0;				1;12 ;		в)							5			. 9. a									6				2					3		.												6 ,
									3;				5	;2											6		;		2	;				3							10.			a	b
									3;					;2										7			;		7	;		7									10.			a	b
									3
									3

	a	b		14.					11.						a 2 p 5q .																	12.											p	2a				3b .
13.			c		2 p	3q						.		14. а) -6; б) 9;															в)						13;					г) -61; д) 73.
13.			c		2 p	3q					r	.		14. а) -6; б) 9;															в)						13;					г) -61; д) 73.
									13.														arccos					2					.				17. а) -524;									б)		13;
15.			ab b c				ca									16.												2


																													7
в) 3. 18. 4.																	5	.				20. 45 .
						19.				cos							5												21.							x					5i			10 j			10k .
						19.				cos																			21.							x					5i			10 j			10k .
																21
																				1	;		1	. 24.					(			3;3;3).												6.				5.
22.			x		2i	2 j			2k .					23.		1;				1			1																		25.				26.
22.			x		2i	2 j			2k .					23.		1;			2			2																			25.				26.
																			2			2

27.		-11. 28. a)						3; б)						3 3; в) 10										3.			29.					а)				2(k						i ) ; б) 2a						c ;

в) a				c ; г) 3.			30. 50 2.												31.							а) {			3,5,7};												б)		{	6;10;14};

в) { 12;20;28}. 32.														2 6.					33. 5. 7.										4i					3 j					4k . 35. 66;
cos				1		,	cos									4			,			cos									7			.				36.					{	6;	24;8}.

				66												66													66
				66												66													66

37. {7;5;1). 38. 24. 39. ab c 27. 41. 172 . 42. а) Компланарны;

б) не компланарны; в) компланарны. 43. 6. 44. 32 .

3. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ

3.1. Простейшие задачи аналитической геометрии на плоскости

1.Расстояние между двумя точками.

Теорема	1.	Для			любых	двух		точек	M1(x1; y1) и
M 2 (x2 ; y2 )	плоскости				расстояние			d	между ними
выражается формулой

	d		(x	2	x )2	( y	2	y )2 .	(3.1)
				2	1		2	1

2. Площадь треугольника.

Теорема 2. Для любых точек A(x1; y1) , B(x2 ; y2 ) и

C(x3 ; y3 ) , не		лежащих			на	одной	прямой,		площадь			S
треугольника АВС выражается формулой
S	1	(x2	x1) ( y3		y1) (x3		x1 ) ( y2		y1)	.		(3.2)
	1

	2
	2
Пример. Даны точки А(1;1), В(6;4), С(8;2). Найти
площадь треугольника АВС. По формуле (3.2)
S	1	(6	1) (2	1)	(8	1) (4	1)	1	16		8.
	1							1

	2							2
	2							2

3. Деление отрезка в данном отношении. Пусть на плоскости дан произвольный отрезок M1M 2 и пусть М любая точка этого отрезка, отличная от точки M 2 . Число ,

отрезка в данном отношении состоит в том, чтобы по данному

отношению	и данным координатам точек M1	и M 2
найти координаты точки М.
Решить эту задачу позволяет следующая теорема.
Теорема 3. Если точка M (x; y) делит отрезок		M1M 2 ,

в отношении , то координаты этой точки определяются формулами

	x	x1	x2	;	y	y1	y2	,	(3.3)
	x	1		;	y	1		,	(3.3)
		1				1
где (x1; y1 )	координаты точки M1 , (x2 ; y2 )								координаты
точки M 2 .
С л е д с т в и е.			Если M1(x1; y1)				и M 2 (x2 ; y2 ) две
произвольные	точки	и	точка		M (x; y)		середина отрезка
M1M 2 , то	1 , и по формулам (3.3) получаем
			49

;

y1 y2

Таким образом, каждая координата середины отрезка

равна полусумме соответствующих координат.

Пример.

Даны точки

M1 (1;1)

и M 2 (7;4) . Найти точку

M (x; y) , которая в два раза ближе к

M1 , чем M 2 .

Решение. Искомая

точка

М делит отрезок M1M 2 в

отношении

Применяя

формулы (3.3), находим

координаты этой точки:

x 3 ,

2 .

3.2. Полярные координаты

Наиболее важной после прямоугольной системы координат является полярная система координат. Она состоит из некоторой точки О, называемой полюсом, и исходящего из нее луча ОЕ полярной оси. Кроме того, задается единица масштаба для измерения длин отрезков.

Пусть задана полярная система координат и пусть М произвольная точка плоскости. Пусть расстояние точки М от точки О; угол, на который нужно повернуть полярную ось для совмещения с лучом ОМ (рис. 13).

Рис. 13

Полярными координатами точки М называются числа

и . При этом число			считается	первой координатой и
называется	полярным		радиусом,	число	второй
координатой и называется полярным углом.
Точка	М с	полярными координатами			и
обозначается так: М (		;	). Очевидно,	полярный радиус может
иметь любое неотрицательное значение: 0					. Обычно

считают, что полярный угол изменяется в следующих пределах: 0 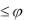2 . Однако в ряде случаев приходится

рассматривать углы, большие 2 , а также отрицательные углы, т. е. углы, отсчитываемые от полярной оси по часовой стрелке.

Установим связь между полярными	координатами точки
и ее прямоугольными координатами. При этом будем
предполагать, что начало прямоугольной системы координат
находится в полюсе, а положительная полуось абсцисс
совпадает с полярной осью. Пусть	точка М имеет

прямоугольные координаты х и у и полярные координаты			и
(рис. 14). Очевидно,
x	cos , y	sin .	(3.4)

Рис. 14

Формулы (3.4) выражают прямоугольные координаты через полярные. Выражения полярных координат через прямоугольные следуют из формул (3.4):

<<< < Предыдущая 1 23 / 53 4 5 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
15.11.20225.62 Mб13471.pdf
#
15.11.20225.66 Mб13474.pdf
#
15.11.20225.76 Mб13478.pdf
#
15.11.20225.76 Mб23479.pdf
#
15.11.20225.79 Mб23483.pdf
#
15.11.20225.8 Mб33484.pdf
#
15.11.20225.83 Mб43487.pdf
#
15.11.20225.83 Mб33489.pdf
#
15.11.20225.85 Mб13490.pdf
#
15.11.20225.85 Mб573491.pdf
#
15.11.20225.85 Mб403492.pdf