
- •ВВЕДЕНИЕ
- •1. ЭЛЕМЕНТЫ СТРУКТУРНОЙ КРИСТАЛЛОГРАФИИ
- •1.1. Пространственная решетка, элементарная ячейка, базис
- •1.2. Кристаллографические индексы плоскостей
- •1.3. Кристаллографические индексы направлений
- •1.4. Индексы Бравэ
- •1.5. Обратная решетка
- •1.6. Зона и правило зон
- •1.7. Вычисление расстояний и углов в кристаллах
- •1.8. Обратная решетка и дифракция рентгеновских лучей
- •1.9. Задачи
- •2.1. Основы метода и используемое оборудование
- •2.2. Профильный анализ
- •2.3. Качественный рентгенофазовый анализ
- •2.4. Определение состава многофазной смеси порошков
- •2.5. Определение размера области когерентного рассеяния нанодисперсного материала
- •2.6. Лабораторно-практическая работа «Исследование фазового состава и структуры материалов методом рентгеновской
- •дифрактометрии»
- •3. ЭЛЕКТРОНОГРАФИЯ
- •3.1. Дифракция электронов
- •3.2. Получение электронограмм
- •3.3. Анализ электронограмм
- •3.4. Практическое задание по теме «Электронография»
- •4.1. Основы метода сканирующей зондовой микроскопии
- •5. ОЖЕ-СПЕКТРОСКОПИЯ
- •5.2. Историческая справка
- •5.3. Физические основы метода Оже-электронной спектроскопии
- •5.4. Кинетическая энергия Оже-электронов
- •5.5. Оборудование для ОЭС
- •5.7. Качественный анализ
- •5.8. Количественный анализ
- •БИБЛИОГРАФИЧЕСКИЙ СПИСОК
- •ПРИЛОЖЕНИЕ
- •ОГЛАВЛЕНИЕ
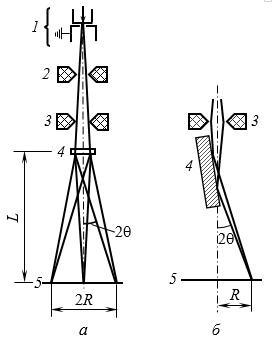
3.2. Получение электронограмм
Электронограммы получают либо в электронографах, либо в просвечивающих электронных микроскопах, работающих в режиме дифракции или микродифракции. Для получения электронограмм используют две геометрии съемки:
-при прохождении электронного пучка сквозь тонкий (около 0,1 мкм) образец (съемка «на просвет») (рис. 3.4 а),
-при «скольжении» электронного пучка под углом до 3° вдоль плоской поверхности массивного образца (съемка «на отражение») (рис. 3.4 б).
Фокусировка электронов в плоскости флуоресцентного экрана 4 осуществляется линзами 2 и 3. Регистрацию электронограмм осуществляют на фотопленку или на полупроводниковую матрицу с зарядовой связью (ПЗС-матрицу).
Рис 3.4. Схема, иллюстрирующая формирование дифракционной картины в электронографе в режиме «на просвет» (а) и в режиме «на отражение» (б): 1 – электронная пушка; 2 – I линза; 3 – II линза; 4 – исследуемый образец; 5 – экран
Электронограммы, полученные в режиме «на просвет», приведены на рис. 3.2 и 3.3. На рис. 3.5 приведены электронограммы, полученные в режиме «на отражение» для эпитаксиальной (а) и поликристаллической нетекстурированной (б) пленки.
54

а |
б |
Рис. 3.5. Электронограммы, полученные в режиме «на отражение», эпитаксиальной (а) и поликристаллической нетекстурированной (б) пленки ниобата лития на поверхности кремниевой пластины
Поскольку на электронограммах формируются лишь максимумы с малы-
ми углами, уравнение Вульфа-Бреггов можно представить в виде: |
|
||||||||||||
|
|
|
|
2θ |
|
|
|
λ |
/ |
|
(3.4) |
||
|
|
hkl – расстояние от |
= 2θ = |
|
|
||||||||
|
|
Как следует из рис. 3.3, |
для малых углов |
|
|
|
|||||||
|
|
|
2 |
|
|
θ = . |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
, |
(3.5) |
|
|
|
|
|
|
|
|
|
|
|
|
||
где R |
|
|
нулевого максимума (формируемого первичным лучом) |
||||||||||
до дифракционного максимума |
|
|
в случае электронограммы от монокристал- |
||||||||||
|
|
|
|
|
|
кольца в случае электронограммы от поликри- |
|||||||
ла или радиус дифракционного |
|
|
|
|
|
|
|||||||
сталла. |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Таким образом, выражение (3.5) можно записать |
|
||||||||||
где |
|
· |
– постоянная прибора. · |
= · · , |
(3.6) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
3.3.Анализ электронограмм
По л и к р и о т а л л и ч е с к и е о б р а з ц ы .
Анализ электронограмм от поликристалла сводится к определению межплоскостных расстояний dhkl согласно формуле (3.6) и типа кристаллической решетки путем сопоставления набора полученных межплоскостных расстояний
сданными баз межплоскостных расстояний.
Мо н о к р и с т а л л и ч е с к и е о б р а з ц ы .
55
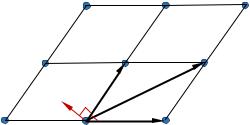
При работе с монокристаллическими образцами известной структуры и неизвестной ориентировкой индицирование точечной электронограммы можно произвести путем сопоставления ее с электронограммами, построенными
для различных ориентировок монокристалла относительно электронного луча. |
|||||||||||||||||||||||||||||||||||
[ ] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( ) |
|
|
|
|
|
|
|
|
|
||||||
Построение и индицирование электронограммы для ориентировки кристалла |
|||||||||||||||||||||||||||||||||||
|
|
|
|
сводится к построению плоскости |
|
|
|
|
обратной решетки и исключе- |
||||||||||||||||||||||||||
нию узлов, запрещенных структурным фактором (правилом погасания). |
|
|
|||||||||||||||||||||||||||||||||
|
|
|
Для всех узлов |
, принадлежащих плоскости обратной решетки |
|
, |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
(3.3) |
для |
|
|
|
|
|
|
|
|
|
[ ] |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. Данное условие равнозначно выполне- |
|||||||||||||||||
выполняется условие |
|
|
|
|
для оси зоны |
|
|
. |
|
|
|
|
|
( ) |
|
||||||||||||||||||||
нию условия зональности (1.44) |
= 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
Построение начинается с выбора узла |
|
|
|
с минимальными индексами, |
||||||||||||||||||||||||||||
удовлетворяющими условию зональности |
для заданной оси |
|
|
и правилу |
|||||||||||||||||||||||||||||||
|
1 1 1 |
|
|
решетки, соответст- |
|||||||||||||||||||||||||||||||
погасания для решетки кристалла. Длина вектора обратной |
|
[ ] |
|
|
|
||||||||||||||||||||||||||||||
|
|
|
1 1 |
1 |
|
|
1 1 1 |
|
1 1 1 |
|
|
|
2 2 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
вующего узлу, определяется из значения межплоскостного расстояния плоско- |
|||||||||||||||||||||||||||||||||||
сти ( |
|
|
|
|
): | |
|
|
|
) |
| = 1/ |
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
) и ( |
|
|
|
|
1 1 1 |
|
2 2 2 |
|
k l выбирается аналогично первому. Угол |
|||||||||||||||||||||
|
1 |
|
В общем случае второй узел h |
||||||||||||||||||||||||||||||||
|
1 1 |
|
|
|
2 2 2 |
|
|
|
и |
|
|
|
|
определяется как угол между плоскостями |
|||||||||||||||||||||
между векторами |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
( |
|
= 1 |
+ 2 |
|
3 |
по соответствующему решетке кристалла соотношению из |
|||||||||||||||||||||||||||||
3 |
|
= 1 + 2( ) |
|
третий |
|
узел |
с индексами |
|
|
|
, |
||||||||||||||||||||||||
приложения |
А. |
Затем |
строится |
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
. Трансляцией |
|
полученной |
примитивной |
ячейки |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 = 1 + 2 |
|
|||||||||||||||
можно построить плоскость |
|
|
|
обратной решетки кристалла (рис. 3.6). |
|
||||||||||||||||||||||||||||||
[uvw]
2 |
2 2 |
3 3 3 |
|
|
|
2 2 2 |
|
|
|
3 3 3 |
|
|
|
1 1 1 1 |
1 1 |
Рис. 3.6 Схема общего случая построения[ точечной] электронограммы для оси зоны
При построении электронограммы для кубических кристаллов удобно
выбирать второй узел таким, чтобы выполнялось условие нормальности векто- |
||||||||||||
выражением: |
|
1 1 1 |
|
2 2 2 |
(рис. 3.6). Это условие определяется |
|||||||
ров обратной решетки |
|
|
+ |
|
|
|
||||||
Таким образом, |
|
2 |
+ |
2 |
= 0. |
|
|
|||||
|
|
1 |
2 |
1 |
|
|
1 |
|
|
(3.7) |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
поиск индексов для второго узла |
|
для кристалла с |
|||||||||
кубической решеткой можно осуществить с помощью |
полученного решением |
|||||||||||
2 2 2 |
|
|||||||||||
56

системы уравнений |
|
|
|
|
|
|
|
1 |
+ 1 |
+ 1 = 0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
+ 2 + 2 = 0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
выражения |
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
|
+ 1 |
2 |
|
+ 1 2 |
= 0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h ,k ,l |
|
|
= |
l1 |
|
k1 |
, |
h1 |
, |
l1 |
, |
k1 |
h1 |
. |
|
|
|
|
|
|
|
|
(3.8) |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
. Если для |
|
|
|
|
|
2 |
|
2 |
|
2 |
w |
, |
|
|
v |
|
|
u |
|
|
|
|
|
|
|
1 1 1 |
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
|
|
2 |
|
|
|
|
w |
|
v |
|
|
|
|
u |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
После определения индексов |
|
|
|
, |
|
|
|
, |
|
|
|
|
на оси, нормальной вектору |
|
|
|
|
|
, |
|||||||||||||||||||||||||||||||||||||||||||||
строится |
узел |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
имеется наибольший общий |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
индексов |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 2 2 |
|
строится |
|
|
|
|
|
|
2 |
|
2 |
2 |
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
делитель |
|
|
|
|
равный 1, и отражение |
|
|
2 |
22 |
22не2 |
запрещено правилом погаса- |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
оси |
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
== |
2 |
2 2 |
соответствует |
||||||||||||||||||||||||||||||||||||||
ния, то |
|
на |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
узел |
|
|
|
|
|
|
|
|
|
|
|
, |
которому |
|||||||||||||||||||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
2 |
2 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
3 |
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
3 |
|
|
+ 2/ |
|
|
3 |
= 1 + 2 |
/ |
|
|||||||||||||||||||||||||
= 1 |
+ |
|
2/ (рис. 3.6). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= 1 |
|
|
|
|
|||||||||||||||||||||||||||||||||||
тор |
|
|
|
|
|
|
имеющий длину |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
(рис. 3.6). |
|
|
|||||||||||||||||
|
|
Третий |
узел |
|
определяется |
|
|
как |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
2 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 2 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
3 3 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 3 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 2 2 |
|
|
|
|
|
1 1 1 |
|
|
|
|
1 1 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
Рис. 3.7 Схема построения точечной электронограммы |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
для кристалла кубической симметрией для оси зоны [uvw] |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(для данной схемы m=2, n=3) |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
при |
|||
на |
|
При наличии наибольшего общего делителя n к индексам , |
|
, |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
оси |
. 3 3 3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
3 |
3 |
|
|
|
|
|
|
|
3 |
3 |
3 = |
||||||||||||||||||||||
котором отражение |
|
3 |
3 |
|
3 не запрещено правилом погасания, |
оно отмечается |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
3 |
3 |
|
3 |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
При |
|
|
|
|
|
|
|
|
2 2 |
2 |
вектора |
3 3 3 |
|
будет |
равна |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
этом длина |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
ную ячейку плоскости ( ) |
|
|
|
|
|
и (или) |
|
|
|
|
|
|
> 1, > 1 |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
1 |
|
3 |
3 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
|
|
|
|
|
) примитив- |
||||||||
|
|
При наличии отражений |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
обратной решетки можно построить на векторах
57

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
3 |
и |
|
|
|
2 |
или |
|
|
|
и |
|
1 |
|
1 1 |
. |
3 |
3 |
|
|
2 |
2 |
|
|
3 |
3 |
3 |
|
|
|
|||||
На практике более распространены случаи, когда структура кристалла неизвестна, но известен его химический состав. Анализ электронограмм в этом
случае производится путем выполнения следующих операций: |
|
|||
и равноудаленных |
|
|
между парами рефлексов, противолежащих |
|
- измерения расстояния |
|
|||
(рис. 3.8); |
относительно центра электронограммы (или измерения рас- |
|||
|
|
|
= /2) |
|
стояния от центра электронограммы до отдельных рефлексов |
|
|||
Рис. 3.8 Анализ |
|
|
рефлексами |
|
|
|
между |
|
|
|
|
электронограммы: измерение расстояний |
|
|
|||||
(рис. 3.9); |
|
|
за |
|
|
, |
|
|
|
- измерения углов φ между векторами дифракции |
|
т.е. между плос- |
|||||||
костями, |
отвечающими |
|
появление соответствующих |
рефлексов |
|
||||
Рис. 3.9 Анализ электронограммы: измерение углов между векторами дифракции
- идентификации кристаллической фазы путем сравнения полученных по соотношению (3.6) межплоскостных расстояний с табличными значениями
58
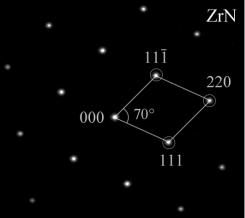
для предполагаемой фазы;
( 2 |
- подтверждения структуры кристаллической фазы путем сопоставления |
|||
2 2) |
|
|
и |
|
измеренных на электронограмме углов между парами плоскостей |
|
|||
|
и расчетных углов между теми же плоскостями в |
кристалле (слож- |
||
|
|
( 1 1 1) |
|
|
ность этой процедуры может заключаться в наличии семейств плоскостей с |
|||||||
костей, |
|
|
|
|
|
|
|
одинаковыми межплоскостными расстояниями и различными комбинациями |
|||||||
индексов |
; в этом случае необходимо, определив все возможные пары плос- |
||||||
|
установить наличие пары, расчетный угол между которыми соответст- |
||||||
вует измеренному); |
( ) |
|
|
|
|||
ем, а углы между |
|
|
|
|
|||
- присвоения рефлексам индексов таким образом, чтобы все узлы плоско- |
|||||||
сти обратной решетки |
|
были связаны друг с другом векторным сложени- |
|||||
- определения по |
|
|
соответствовали расчетным (рис. 3.10); |
||||
|
|
|
парами векторов |
|
|||
соотношению (1.46) оси зоны кристалла.
Рис. 3.10. Анализ электронограммы( ) : построение примитивной ячейки плоскости обратной решетки
Задача анализа электронограмм заметно усложняется, если на ней имеются отражения от двух и более кристаллов; возникают дополнительные отражения, связанные с наличием субзеренной структуры; возникают отражения, принадлежащие нескольким зонам вследствие искривления образца. Наибольшую сложность представляет анализ электронограмм от образцов с неизвестным составом и структурой. В указанных случаях задачу анализа можно упростить, если получить несколько электронограмм с различными осями зон для одного и того же участка образца путем его наклона под различными углами по отношению к электронному пучку. Такой способ приводит к получению большего набора межплоскостных расстояний по сравнению с однократной съемкой электронограммы.
59
