
Элементы линейной алгебры. Глушко Е.Г., Дубровская А.П
.pdf
Таким образом,  т.е. в
т.е. в
ортонормированном базисе скалярное произведение двух любых элементов равно сумме произведений соответствующих координат этих элементов.
|
Выясним смысл координат элемента |
|
|
||||||
|
x относительно |
||||||||
базиса |
|
|
|
По |
условию |
|
|
|
|
e1 |
,e2 |
,..., en . |
x |
=x1 e |
1+x2 e 2+ |
+xn e n. |
|||
|
|
|
|
|
|
|
|
|
|
Умножим скалярно обе части этого равенства на элемент e k |
|||||||||
|
|
|
|
|
|
|
|
|
|
(любой из системы e1 |
,e2 ,..., en ). Используя аксиомы скалярного |
||||||||
произведения и определениe ортонормированного базиса, получаем:
|
|
n |
|
|
n |
|
|
|
|
|
xk . |
||||||
x,ek |
|
xi ,ei |
,ek |
|
xi ei |
,ek |
||
|
|
i 1 |
|
i |
1 |
|
|
|
Таким образом, координаты элемента x в ортонормированном базисе равны скалярному произведению этого элемента на соответствующие базисные элементы.
Эти координаты часто называют проекциями элемента на соответствующие базисные элементы. Рассмотрим теперь в n - мерном евклидовом пространстве En совершенно произвольный (вообще говоря, не ортонормированный) базис
|
|
|
f1, f2 ,..., fn .
Рассуждая аналогично предыдущему случаю, получим,
|
|
|
что в произвольном базисе f1, f2 ,..., fn скалярное произведение
двух любых элементов: |
|
|
|
|
|
|
|
|
=x1 |
|
|
|
|||
x |
f 1+x2 f 2+ +xn f n |
|
|||||
и |
|
|
|
|
|
|
|
|
|
|
|
|
|||
y |
=y1 |
f 1+y2 f 2+ +yn f n |
|
||||
определяется равенством: |
|
|
|
|
|
||
|
|
|
n |
|
k |
|
|
|
|
|
|
, |
|
||
|
x, y |
|
|
aik xi yk |
|
||
|
|
|
i 1 |
i |
1 |
|
|
в котором матрица |
(aik) |
|
(i,k=1,2, ,n) |
имеет |
элементы |
||
111

aik=( f i, f k). Отсюда следует, что для того чтобы в данном
базисе f1, f2 ,..., fn евклидова пространства En скалярное
произведение двух элементов было равно сумме произведений соответствующих координат этих элементов, необходимо и
|
|
|
достаточно, чтобы базис f1, f2 ,..., fn был ортонормированным.
Упражнения.
1.Пусть X =(x1,x2) и Y =(y1,y2) - произвольные векторы арифметического пространства R2. Показать, что скалярное произведение в R2 можно определить следующими
способами: |
|
|
|
||
a) |
( X |
,Y ) = 2x1y1+5x2y2; |
|
|
|
б) |
( X |
,Y ) = x1y1+x1y2+x2y1+x2y2. |
|
Вычислить скалярное произведение векторов: |
|
|
|
|
X |
=(1,-2) и Y |
=(5,1) каждым из указанных способов. |
2.Доказать, что в пространстве n многочленов
степени не выше n скалярное произведение многочленов: p(t)=a0+a1t+ +antn
и
q(t)=b0+b1t+ +bntn
можно определить способами: |
|
||
а) |
(p,q)=a0b0+a1b1+ +anbn; |
|
|
|
|
n |
|
б) |
(p,q)= |
p(tk )q(tk ) , t1,t2, |
,tn - произвольные |
|
|
k 1 |
|
попарно различные действительные числа. |
|||
Вычислить |
скалярное произведение многочленов |
||
p(t)=1+t+t2 |
и q(t)=t-2t2+3t3 каждым |
из указанных способов |
|
(n=4), если в случае б) t1= -2, t2= -1, t3=1, t4=2.
3.Проверить ортогональность следующих систем векторов в евклидовом пространстве Rn и дополнить их до
ортогональных базисов: |
|
|
|
|
|
1) |
e 1=(1,-2,1,3), |
e 2=(2,1,-3,1) |
112
2)e 1=(1,1,1,1,1), e 2=(1,0,0,1,-2), e 3=(2,1,-1,0,2)
|
|
|
3) |
e 1=(2/3,1/3,2/3), |
e 2=(1/3,2/3,-2/3) |
|
|
|
4) |
e 1=(1,1,1,2), |
e 2=(1,2,3,-3). |
4.Доказать, что в вещественном евклидовом
пространстве обратная: два тогда, когда:
справедлива теорема Пифагора, а также ей
вектора x и y ортогональны тогда и только
| + |2=| |2+| |2. x y x y
|
|
|
|
Ответы. |
|
|
|
|
|
|
1. |
а) |
0; |
б) |
-6. |
|
|
|
|
|
|
2. |
а) |
-1; |
б) |
24. |
|
|
|
|
|
|
3. |
1) |
|
|
|
|
|
|
|
|
|
e 3=(-4,2,-1,3), e 4=(2,4,3,1). |
|
|
|
|
||||||
|
Указание. |
Для |
определения |
вектора |
e 3=(x1,x2,x3,x4) |
|||||
достаточно |
найти |
какое-нибудь |
решение |
системы |
||||||
относительно |
неизвестных |
x1,x2,x3,x4 |
двух |
линейных |
||||||
|
|
|
|
|
|
|
|
|
|
|
уравнений |
( e 3, |
e 1)=0, |
( e 3, |
e 2)=0. |
Для |
определения |
e 4 |
|||
аналогичная система состоит из трех уравнений. |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
2) |
e 4=(1,-1,1,-1,0), |
e 5=(0,5,1,-4,-2), |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
3) |
e 3=(2/3,-2/3,-1/3), |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
4) |
e 3=(1,-2,1,0), e 4=(25,4,-17,-6). |
|
|
|
|
||||
6. ЛИНЕЙНЫЕ САМОСОПРЯЖЕННЫЕ ОПЕРАТОРЫ В ЕВКЛИДОВОМ ПРОСТРАНСТВЕ 6.1. Понятие сопряженного оператора.
Его свойства
113

Будем |
рассматривать линейные |
операторы |
|
в |
конечномерном |
евклидовом пространстве |
En. Оператор |
|
* |
A |
: |
En En называется сопряженным к линейному оператору A ,
если для любых |
|
и |
|
из En выполняется соотношение: |
||||
x |
y |
|||||||
|
|
|
|
|
|
|
|
* |
|
|
|
( A x |
, y )=( x |
, A |
y ). |
||
Легко убедиться в том, что оператор A *, сопряженный к
линейному оператору A , сам является линейным оператором. Действительно:
|
|
|
1+ |
|
|
|
|
|
|
|
|
|
|
|
( A x , |
y |
y 2)= ( A x |
, y 1)+ ( |
A x |
, y 2)= |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
* y |
1)+ |
* y |
* |
|
1+ |
|
||||||||
= ( x |
, A |
|
( x |
, A |
2)=( x , |
A |
( |
|
y |
y 2)), |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Это соотношение справедливо для любых x |
, |
y 1, y 2 |
и любых |
|||||||||||
чисел и . |
|
Каждый |
линейный |
|
оператор |
A имеет |
||||||||
Теорема. |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
единственный сопряженный.
Отметим следующие свойства сопряженных операторов.
1.I* = I,
2.( A + B )*= A *+ B *,
3. |
( |
* |
* |
A ) = |
A , |
4.( A *)*= A ,
5.( A B )*= B * A *
Доказательства свойств 1-4 элементарны и мы предлагаем провести их самостоятельно.
Докажем свойство 5. Действительно, по определению
произведения операторов имеем ( A ) x = A ( x ). Используя
B B
теперь определение сопряженного оператора получаем
следующую цепочку соотношений: |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
* |
|
|
* * |
|
|
(( A B ) x |
, y )=( A ( B x ), y )=( B x |
, A |
y )=( x |
,( B |
A |
) y ). |
||||||
|
|
|
|
|
|
* * |
|
|
|
|
|
|
Таким образом, (( A |
B ) x |
, y )=( x |
,( B |
A |
) y ), а это означает, что |
|||||||
оператор B * A * является сопряженным к оператору A B .
114

|
|
Если |
оператор |
A |
в |
ортонормированном |
базисе |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
евклидова |
пространства |
имеет |
|
|
матрицу |
|
A=(aij), то |
||||||||
сопряженный оператор |
* |
в том же базисе имеет матрицу |
|||||||||||||
A |
|||||||||||||||
A*=AT. Справедливость утверждения проверить самим. |
базисе |
||||||||||||||
|
|
Пример. |
|
Линейный |
оператор A : E3 |
E3 |
в |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B'=( e |
'1, e '2, e '3) имеет матрицу: |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
1 |
1 |
3 |
|
|
|
|
|
|
|
|
|
|
|
AB |
0 |
5 |
|
1 . |
|
|
|
|
||
|
|
|
|
|
|
|
2 |
7 |
3 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Известно, |
что |
e1 = e 1+2 e |
|
2+ e 3, |
e2 |
= e |
1+ e |
2+2 e 3, |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
e3 |
= e |
1+ e 2 |
и |
базис B=( e1 |
, e2 |
, e3 ) ортонормирован. Найти |
|||||||||
|
|
|
|
|
|
|
|
|
* |
в базисе B'. |
|
|
|
||
матрицу сопряженного оператора A |
|
|
|
|
|||||||||||
|
|
Прежде всего проверим, будет ли ортонормированным |
|||||||||||||
базис B': |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
e1 |
e2 = 1+2+2 = 5 |
0. |
|
|
|
|
||||
Таким образом, базис B' не является ортонормированным, а следовательно, чтобы воспользоваться утверждением о связи
матриц оператора A и A *, надо найти матрицу оператора A в
ортонормированном базисе B, по полученной матрице найти |
|||||
матрицу AB*, а затем, используя формулы перехода, найти |
|||||
матрицу AB'*. Итак, имеем: |
|
|
|
||
|
|
1 |
1 |
1 |
|
TB B |
2 |
1 |
1 . |
||
|
|
1 |
2 |
0 |
|
Тогда: |
|
|
|
|
|
|
1 |
2 |
2 |
0 |
|
T 1 |
1 |
1 |
1 , |
||
|
|||||
2 |
|||||
|
3 |
1 |
1 |
||
|
|
||||
115
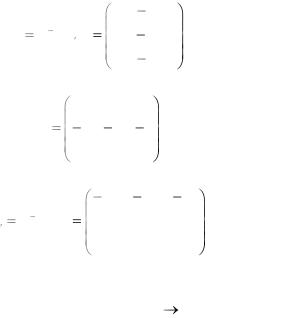
следовательно, |
|
|
|
|
|
|
|
|
|
|
|
2 |
3 |
7 |
|
A |
|
T 1 A T |
6 |
4 |
6 ; |
|
|
B |
|
B |
|
|
|
|
|
|
|
|
|
6 |
5 |
5 |
|
и |
|
|
|
|
|
|
|
|
|
|
2 |
6 |
6 |
|
|
|
|
A* |
3 |
4 |
5 . |
|
|
|
|
B |
|
|
|
|
|
|
|
|
7 |
6 |
5 |
|
|
Отсюда окончательно получаем: |
|
|
|
|
|||
|
|
|
|
36 |
37 |
15 |
|
A* |
T |
1 A*T |
30 30 14 . |
|
|||
B |
|
B |
|
|
|
|
|
|
|
|
26 |
27 |
9 |
|
|
6.2. Самосопряженные операторы |
|
||||||
Линейный |
|
Их свойства |
En |
называется |
|||
оператор A : |
|
En |
|||||
|
|
|
|
|
|
|
|
самосопряженным, если справедливо равенство: |
|
||||||
|
|
|
* |
|
|
|
|
|
|
|
A = |
A . |
|
|
|
Простейшим |
примером |
самосопряженного |
оператора |
||||
является тождественный оператор I. |
действующий в |
||||||
Самосопряженнный |
оператор A , |
||||||
|
|
|
|
|
|
|
|
евклидовом пространстве, называется симметричным оператором.
Теорема. Чтобы оператор A был симметричным, необходимо и достаточно, чтобы в ортонормированном базисе его матрица была симметрической.
Доказательство. Пусть A - симметричный оператор. |
||||||
|
|
|
|
|
|
|
|
|
|
и |
справедливо равенство |
||
Тогда при любых x |
y |
|||||
|
|
|
|
|
|
|
( A x |
, y )=( x |
, A y ). |
Пусть A - матрица оператора A , |
|||
116
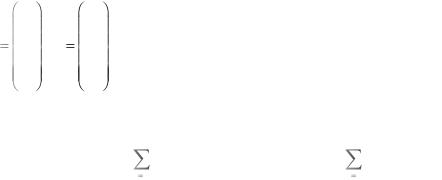
x1 y1
X |
x2 , Y |
y2 - матрицы-столбцы, элементами которых |
|
|
xn |
yn |
|
|
|
|
|
|
|
|
являются координаты векторов |
|
|
|||||||||
x |
и y в ортонормированном |
||||||||||
базисе. |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
n |
|
|
|
|
n |
|
|
|
|
|
yi |
|
|
T |
T |
xi yi , то |
||
|
|
Так как ( x |
, y )= xi |
, а матрица X Y=Y X= |
|||||||
|
|
|
|
|
i 1 |
|
|
|
|
i 1 |
|
T |
T |
|
|
|
|
|
матричную |
форму |
записи |
||
( x |
, y )=X Y=Y X. Используя эту |
||||||||||
скалярного произведения в евклидовом пространстве, получаем:
|
|
|
|
T |
T T |
|
( A x |
, y )=(AX) Y=X A Y, |
|||||
|
|
|
T |
|
T |
AY. |
( x |
, A y )=X (AY)=X |
|||||
Отсюда следует, что XTATY = XTAY, где X и Y произвольные матрицы - столбцы. Это равенство справедливо тогда и только тогда, когда AT = A, т.е. A - симметрическая матрица.
Линейный оператор A в евклидовом пространстве называется ортогональным, если A A *= A *A=E, т.е. A *= A -1.
Теорема. Для того чтобы оператор A был ортогональным необходимо и достаточно, чтобы в любом
ортонормированном базисе его матрица A удовлетворяла соотношению A-1 = AT.
Такие матрицы называются ортогональными. Матрица, обратная ортогональной, также ортогональна.
Справедливо следующее утверждение: матрица Т перехода от одного ортонормированного базиса к другому ортонормированному базису является ортогональной.
Установим ряд важных свойств самосопряженных операторов.
Теорема. Собственные значения самосопряженного оператора вещественны.
117

|
Доказательство. |
Пусть |
- |
собственное |
значение |
||||||||||
самосопряженного |
оператора |
A . |
|
По |
определению |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
собственного значения |
оператора A , |
существует |
ненулевой |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
такой, что |
|
|
|
|
|
|
|
|
|
|
|||
вектор x |
A x = |
x . Из этого соотношения следует, |
|||||||||||||
что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
вещественное скалярное произведение ( A x , x ) может |
|||||||||||||||
быть |
представлено |
в |
|
|
|
|
|
|
|
. Так |
как |
||||
виде ( A x |
, x )= |
( x |
, x )= |
x |
|
||||||||||
|
|
|
|
|
вещественны, то и |
- вещественное число. |
|
||||||||
( A x |
, x ) и |
|
x |
|
|
||||||||||
|
Теорема. Если |
A |
- самосопряженный |
оператор, |
то |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
собственные векторы, отвечающие различным собственным значениям этого оператора, ортогональны.
Доказательство. Пусть |
1 |
и |
2 |
различные собственные |
||||||||||||
значения ( |
1 |
2) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
самосопряженного оператора A , а |
x 1 и |
x 2 - |
||||||||||||||
соответственно отвечающие им собственные векторы. |
|
|||||||||||||||
Тогда |
|
|
|
|
1, |
|
|
|
|
|
|
Поэтому |
скалярные |
|||
A x 1= |
1 x |
|
A x 2= 2 x 2. |
|||||||||||||
произведения ( |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
A x 1, x 2) и ( x 1, |
A x 2) соответственно равны: |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( A x 1, x 2)= |
1( x |
1, x 2), |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
( x 1, |
A x 2)= |
2( x |
1, x 2). |
|
|
|
||||||
Но |
по |
условию |
|
|
|
- |
самосопряженный |
оператор, |
||||||||
A |
|
|||||||||||||||
|
|
|
|
2)=( |
|
|
|
|
|
|
|
|
|
|
|
|
поэтому ( A x |
1, x |
x 1, A x 2). |
|
|
|
|
|
|
|
|||||||
Вычитая из первого соотношения второе, получаем: |
|
|||||||||||||||
|
|
1- |
|
|
|
2)=( |
|
|
|
|
|
|
|
|
|
|
|
( |
2)( x |
1, x |
A |
x |
1, x |
2)-( x |
1, A |
x 2)= |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
=( x 1, |
A |
x 2)-( x 1, A x 2)=0. |
|
|
|
|||||||
Так как |
1 |
|
2, то ( x 1, x 2) = 0, т.е. x 1 и x 2 ортогональны. |
|||||||||||||
Теорема. |
У |
каждого |
самосопряженного |
линейного |
||||||||||||
|
действующего |
в n - мерном евклидовом |
||||||||||||||
оператора A , |
||||||||||||||||
пространстве En, |
существует n линейно независимых попарно |
|||||||||||||||
ортогональных и единичных собственных векторов. |
|
|
||||||||||||||
Таким образом, в n - мерном евклидовом пространстве |
||||||||||||||||
всегда можно |
|
построить |
ортонормированный |
базис |
из |
|||||||||||
собственных векторов симметрической матрицы
118

самосопряженного oператора A . Отсюда следует, |
что всякая |
|
|
|
|
симметрическая матрица A всегда может быть приведена к |
||
диагональному виду, т.е. найдется такая матрица |
T, что T- |
|
1AT=( i ij). Здесь i - собственные значения матрицы A, а: |
||
0, i |
j |
|
ij= 1, i |
j . |
|
При этом матрицу Т можно выбрать ортогональной, т.е. такой что Т-1=ТТ.
6.3. Степенной метод приближенного нахождения собственных значений оператора, действующего в En
Пусть требуется вычислить максимальное по модулю
собственное значение 1 |
матрицы оператора A , действующего |
|
|
в евклидовом n-мерном пространстве En, причем известно, что
| 1| | 2| |
| 3| |
|
| n|. |
|
|
|
|
|
|
|
|
|
|
|
|
|
Алгоритм простейшего варианта степенного метода |
||||||||||||||||
состоит |
в |
следующем. |
Возьмем |
произвольный |
начальный |
|||||||||||
вектор |
|
(0) и построим |
последовательность |
векторов |
|
|||||||||||
x |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
1(k)} к |
1 по следующим |
||||||
{ x (k)} |
k=0, |
, |
и приближений { |
|||||||||||||
формулам: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
x (k)= |
A x (k-1), |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(x(k ) , x( k 1) ) |
|
. |
|
|
|
|
|
|||
|
|
|
|
1(k)= |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
(x(k 1) , x( k 1) ) |
|
|
|
|
||||||
Можно |
показать, |
что |
последовательности |
{ x |
(k)} |
и |
||||||||||
{ 1(k)} |
сходятся соответственно к пределам |
|
1, где |
1 - |
||||||||||||
x и |
||||||||||||||||
искомое |
собственное значение |
и |
|
|
- |
соответствующий |
||||||||||
|
x |
|||||||||||||||
собственный вектор. Процесс нахождения последовательности приближений заканчивают, как только норма разности между соседними приближениями будет меньше заданной точности.
Упражнения
119
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
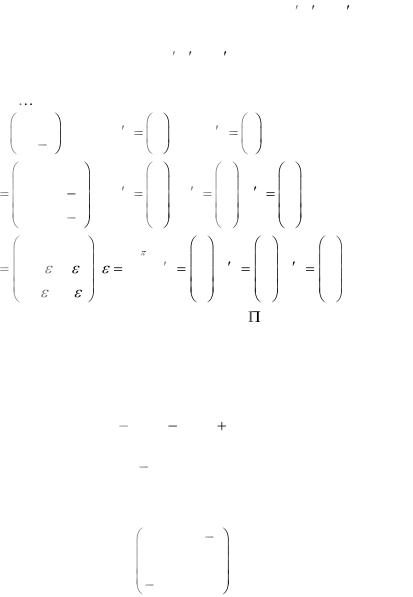
1.Линейный оператор |
|
A |
|
в базисе B'=( e1 |
,e2 ,..., en ) имеет |
||||||||||||||||||||||||||||
матрицу A. Найти матрицу сопряженного оператора |
|
* |
в том |
||||||||||||||||||||||||||||||||
A |
|
||||||||||||||||||||||||||||||||||
же базисе B', если векторы |
|
|
|
|
|
|
|
|
|
заданы столбцами своих |
|||||||||||||||||||||||||
|
|
|
e1,e2 ,..., en |
||||||||||||||||||||||||||||||||
координат |
в |
|
некотором |
|
ортонормированном |
|
базисе |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B=( e 1, |
, e n): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
1) A= |
1 |
2 |
, |
|
|
|
|
|
|
|
|
|
1 |
|
, |
|
|
|
|
|
|
|
1 |
. |
|
|
|
|
|
||||||
1 |
1 |
|
|
|
|
e1 |
|
|
|
|
0 |
|
|
|
e2 |
|
1 |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
1 |
1 |
3 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
2) A |
0 5 |
1 , |
|
|
e1 |
|
|
|
|
2 , |
e2 |
|
|
1 ,e3 |
|
1 . |
|
|
|
||||||||||||||||
|
|
2 |
7 |
3 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
2 |
|
|
|
0 |
|
|
|
|
|||||
|
|
1 |
1 |
1 |
|
|
|
|
|
|
|
2 |
i |
|
|
|
1 |
|
|
|
|
1 |
|
1 |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
3) A 1 |
|
2 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 . |
|
|
|||||||||||
|
|
|
|
|
e 3 , e |
|
|
2 , e |
|
|
1 , e |
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
2 |
|
|
|
3 |
|
|
|
|
||
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
2 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
2. |
|
В |
пространстве |
многочленов |
|
|
3 |
задано |
скалярное |
||||||||||||||||||||||||||
произведение |
|
(f,g)=a0b0+a1b1+a2b2, |
|
где |
|
f(t)=a0+a1t+a2t2, |
|||||||||||||||||||||||||||||
g(t)=b0+b1t+b2t2. Найти матрицы оператора дифференцирования |
|||||||||||||||||||||||||||||||||||
D= |
d |
и сопряженного оператора D* в базисе B: |
|
|
|
||||||||||||||||||||||||||||||
dt |
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1) |
|
B=( |
|
1 |
t |
2 |
|
|
1 |
|
t,t |
2 |
1, |
1 |
t |
2 |
|
1 |
t ); |
|
|
|
|
|
|
||||||||
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
2) |
|
B=(1,t, |
|
3 |
|
t |
2 |
|
|
1 |
|
). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
3. Матрица оператора в некотором ортонормированном базисе имеет вид:
11 2 8 A= 2 2 10 .
8 10 5
а) Найти ортонормированный базис из собственных векторов матрицы A.
120
