Основы теории механизмов и машин. Кирпичев Ю.В., Кирпичев И.Ю
.pdf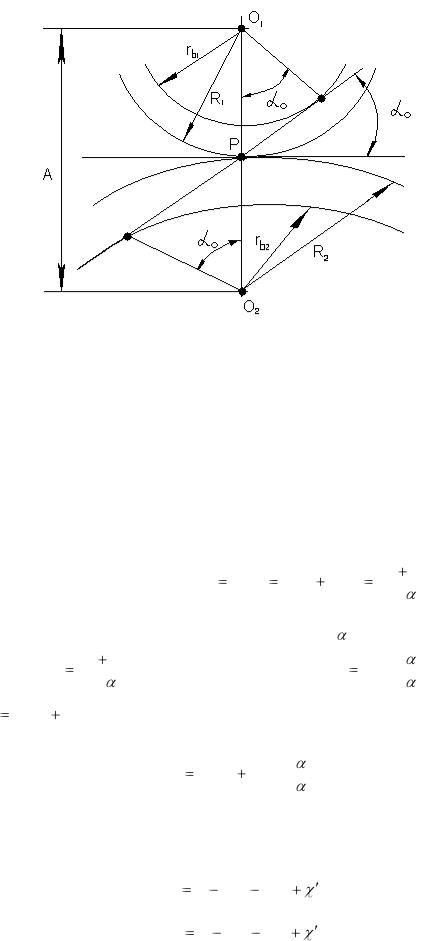
Рис. 5.13. к определению расстояние между центрами колѐс.
5.13. Определение геометрических размеров колѐс со сдвигом
Расстояние A (рис.5.13) между осями колѐс, нарезанных со сдвигом, будет равно
A O1O2 |
O1 P0 |
O2 P0 |
rb1 |
rb2 |
|
cos |
з |
||||
|
|
|
|
|
Т.к. |
|
для колѐс с углом зацепления |
0 |
расстояние A0 между осями |
||||||||||||||
равно |
A |
|
|
rb1 |
rb 2 |
, |
то, |
следовательно |
A |
A |
cos |
0 |
, откуда, так как |
|||||||
|
|
0 |
|
|
cos |
з |
|
|
|
|
|
|
|
|
|
0 |
cos |
3 |
|
|
A |
m |
(z |
z |
|
) окончательно получаем |
|
|
|
|
|
|
|
||||||||
|
2 |
|
|
|
|
|
|
|
||||||||||||
0 |
2 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
m |
(z1 |
z2 ) |
cos |
0 |
|
|
|
|
(5.40) |
|
|
|
|
|
|
|
|
|
2 |
cos |
3 |
|
|
|
|
||||||
|
|
Радиусы Rd 1 |
и Rd 2 |
окружностей головок колѐс 1 и 2 выражаются по |
||||||||||||||||
формулам |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
Rd1 |
A |
RД 2 |
x2 m |
|
m |
|
|
|
(5.41) |
|||
|
|
|
|
|
|
|
|
Rd 2 |
|
A |
RД1 |
x1m |
|
m |
|
|
|
(5.42) |
||
|
|
|
|
|
|
|
|
|
|
|
|
71 |
|
|
|
|
|
|
|
|
Формулы для радиусов R f 1 |
и R f 2 окружностей впадин имеют вид |
||
R f 1 |
RД1 |
m x1m cm |
(5.43) |
Rf 2 |
RД 2 |
m x2 m cm |
(5.44) |
где с=0,25коэффициент радиального зазора.
Коэффициент |
перекрытия может быть определѐн |
по формуле |
|||||
|
|
|
|
|
|
|
|
R 2 |
r 2 |
|
R 2 |
r 2 |
Asin |
, при этом величина шага t |
по начальной |
a1 |
b1 |
|
a 2 |
b2 |
|
||
|
|
|
|
||||
m cos
окружности при условии нарезания колеса со сдвигом должна быть принята равной
tm cos 0 cos 3
Соответственно угол 0 в формуле (для ) должен быть принят равным 3 .
Таким образом, формула для определения коэффициента перекрытия для колѐс, нарезанных со сдвигом, будет иметь следующий вид:
R 2 |
r 2 |
R 2 |
r |
2 |
Asin |
3 |
|
a1 |
b1 |
a 2 |
b2 |
|
(5.45) |
||
|
|
m cos |
3 |
|
|
|
|
|
|
|
|
|
|
||
72
Глава 6. СИНТЕЗ КУЛАЧКОВЫХ МЕХАНИЗМОВ
6.1. Основные виды кулачковых механизмов
Кулачковые механизмы широко применяются в машинах и приборах в качестве передаточных механизмов. Обеспечивающих практически любой закон движения ведомого звена.
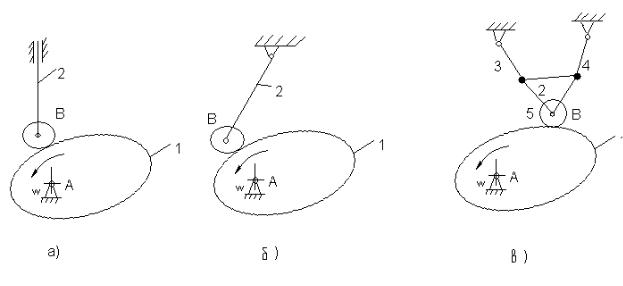
Кулачковые механизмы делят на плоские и пространственные. В свою очередь плоские механизмы, в зависимости от движения ведомого звена делятся на три вида:
1.Ведомое звено движется поступательно
2.Ведомое звено вращается
3.Ведомое звено совершает сложное движение.
Рис.6.1 Схемы кулачковых механизмов.
а) с поступательно движущимся ведомым звеном; б) с возвратновращающимся ведомым звеном; в) со сложно-движущимся ведомым звеном.
Внутри каждого вида кулачковых механизмов можно получить различные разновидности этих механизмов в зависимости от характера движения кулачка, взаимного расположения кулачка и ведомого звена, геометрических форм элемента, принадлежащего ведомому звену.
73
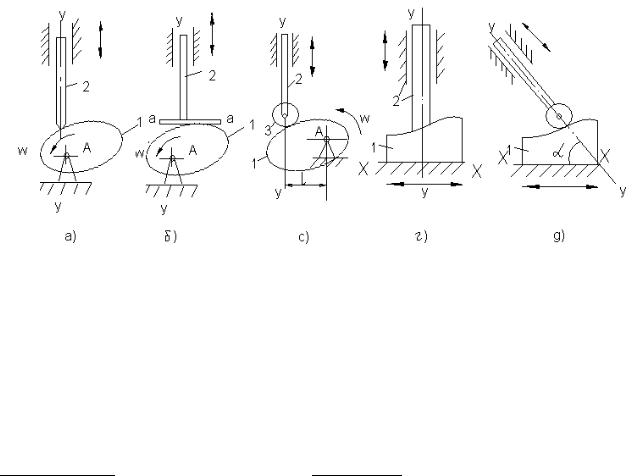
Рис.6.2. Схемы кулачковых механизмов:
а) с поступательно-движущимся толкателем с остриѐм на конце; б) с плоским толкателем;
в) с поступательно-движущимся толкателем и роликом; г) с поступательно-движущимся кулачком и толкателем с остриѐм; д) с поступательно-движущимся кулачком, толкателем и роликом.
Ведомое звено 2, движущееся поступательно, носит название толкателя или штанги.
Ведомое звено 2, вращающееся вокруг неподвижной оси, называется коромыслом (Рис.6.1,в) называется шатуном. Если ось толкателя y-y
проходит через ось вращения кулачка, то механизм называется кулачковым механизмом с центральным толкателем. (Рис.6.2,а) Если ось y-y отстоит на кратчайшее расстояние R от оси A вращения кулачка (6.2,с), то такой механизм называется кулачковым механизмом со смещенным толкателем.
6.2. Исходные данные для проектирования кулачковых механизмов
Законы движения.
Чтобы спроектировать профиль кулачка кулачкового механизма, необходимо выбрать:
а) кинематическую схему механизма; б) закон движения ведомого звена в функции обобщенной
координаты; в) некоторые основные размеры звеньев.
74
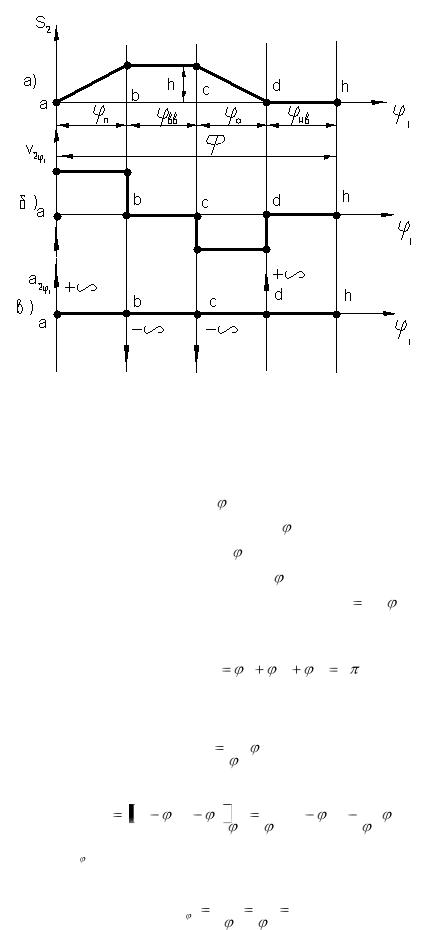
Рис. 6.3. Закон движения ведомого звена кулачкового механизма: а) диаграмма пути; б) диаграмма аналога скорости; в) диаграмма аналога ускорения.
Законы движения ведомых звеньев кулачковых механизмов будем рассматривать для четырѐх характерных фаз движения ведомого звена:
1.Фазы подъѐма - П
2.Фазы верхнего выстоя - |
вв |
3.Фазы опускания - 0 |
|
4.Фазы нижнего выстоя - |
нв |
5.Наиболее простым законом S2 S2 ( 1 ) является линейный закон движения на фазах подъѐма и опускания (рис. 10.3) Сумма углов:
Ф |
n вв |
нв |
2 |
|
|
||
Полный объѐм ведомого звена |
обозначим h1 . Закон движения |
||
ведомого звена на фазе подъѐма представляет собой зависимость
S |
|
h |
|
|
|
|
|
|
(6.1) |
2 |
|
1 |
|
|
|
|
|||
|
|
|
|
|
|||||
|
|
п |
|
|
|
|
|
|
|
А на фазе опускания |
|
|
|
|
|
|
|
|
|
S2 (Ф нв ) |
|
h |
|
h |
(ф |
нв ) |
h |
|
(6.1) |
1 |
|
|
|
1 |
|||||
|
|
0 |
0 |
|
|
0 |
|
|
|
Аналог v2 1 скорости ведомого звена соответственно равен для фазы подъѐма
v |
|
dS2 |
|
h |
const |
(6.3) |
2 1 |
d 1 |
|
|
|||
|
|
|
п |
|
|
А для фазы опуская
75
|
|
v2 |
|
dS2 |
|
d |
|
h |
(Ф |
нв ) |
h |
|
h |
const |
(6.4) |
|
|
1 |
d 1 |
|
d 1 |
|
|
1 |
|
||||||
|
|
|
|
|
0 |
|
|
0 |
|
0 |
|
|
|||
Скорость движения толкателя на обеих фазах постоянна. Аналоги |
|||||||||||||||
ускорений a2 1 |
на обеих фазах равны нулю, кроме положений a,b,c и d, где |
||||||||||||||
функция |
v2 |
1 |
v2 |
1 ( |
1 ) имеет разрывы. В |
этих положениях теоретически |
|||||||||
ускорения |
|
|
a2 1 |
ведомого |
звена |
равны |
бесконечности. Это |
вызывает |
|||||||
появления в механизмах “жѐстких ударов”, при которых силы, действующие на звенья механизма, теоретически достигают бесконечности. Практически ролики на толкателях сглаживают в местах перехода скорости, но всѐ же в указанных положениях происходит размыкание элементов высшей пары и соударение ведомого звена с ведущим. Поэтому линейным законом пользуются только на части фаз подъѐма или опускания и в закон движения вводятся переходные кривые, позволяющие осуществлять плавный переход на участках сопряжения двух линейных законов движения. Такими переходными кривыми могут быть дуги окружностей, участки парабол и т.д.
При проектировании кулачковых механизмов обычно задаются аналоги ускорений ведомого звена. По заданным аналогам ускорений и начальным условиям определяют аналоги скоростей и закон движения ведомого звена. На фазе подъѐма используют следующие аналоги ускорений:
а) равноускоренный; б) синусоидальный; в) косинусоидальный; г) трапецеидальный.
6.3. Определение основных размеров кулачковых механизмов
Основные размеры кулачковых механизмов определяются из кинематических, динамических и конструктивных условий. Кинематические условия определяются тем, что механизм должен воспроизводить заданный закон движения. Динамические условия весьма разнообразны, но основной в том, чтобы механизм имел высокий КПД. Конструктивные требования определяются из условия достаточной прочности отдельных деталей механизма – сопротивляемости износу соприкасающихся кинематических пар. Проектируемый механизм должен обладать наименьшими габаритами.
76
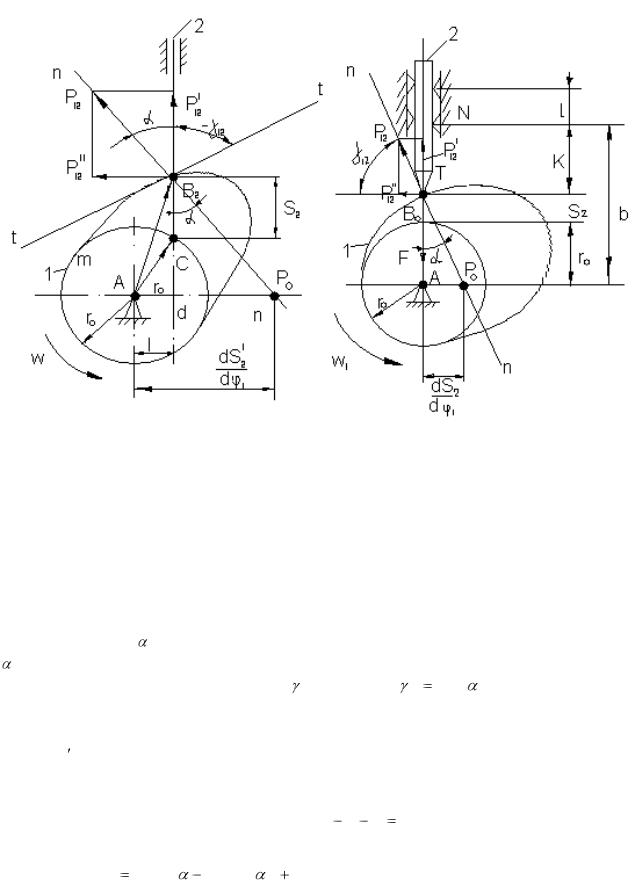
Рис.6.4. К силовому анализу |
|
Рис.6.5. К исследованию |
||
кулачкового |
механизма |
с |
угла |
давления в кулачковом |
поступательно-движущемся |
|
механизме |
||
толкателем. |
|
|
|
|
На рис. 6.4 показан кулачковый механизм с толкателем 2, |
||||
оканчивающийся |
остриѐм |
B2 . |
Если пренебречь трением в высшей |
|
кинематической паре, то сила |
P12 , |
действующая на толкатель 2 со стороны |
||
кулачка 1. Угол , образованный нормалью n-n к профилю кулачка 1. Угол , образованный нормалью n-n и направлением движения толкателя 2, является углом давления а угол 12 , равный 12 90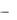 
, является углом передачи. Если рассмотреть равновесие толкателя 2 (рис. 10.5) и подвести все силы к точке B2 , то толкатель будет находиться под действием движущей силы P12 , приведѐнной силы сопротивления T, учитывающей полезные сопротивления, силу пружины, силы инерции, и приведѐнной силы трения F.
Из уравнения равновесия сил, действующих на толкатель 2, имеем
P12 cos
T F 0
Приведѐнная сила трения T равна
T P cos |
fP sin (1 |
2k |
) , |
|
|||
12 |
12 |
l |
|
|
|
||
Где f - коэффициент трения в направляющих; l -длина направляющих;
k - вылет толкателя.
77
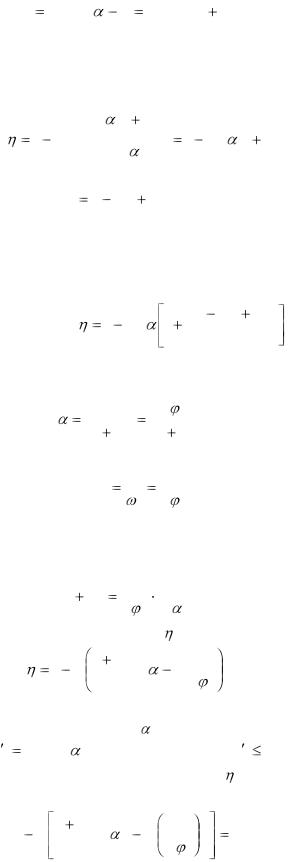
Тогда из уравнения равновесия сил получаем, что сила трения
равна
F P cos |
T fP sin(1 |
2k |
) |
(6.5) |
|
||||
12 |
12 |
l |
|
|
|
|
|
||
Мгновенный коэффициент полезного действия 
механизма без учѐта трения в высшей паре и подшипнике вала кулачка можно определить по формуле
|
|
|
fP |
|
sin |
(1 |
|
2k |
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
||||||||||||
|
|
12 |
|
|
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
ftg |
(1 |
2 |
|
|
) |
(6.6) |
||||
|
|
|
|
P12 cos |
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
|||||||||||||||
Величина вылета k толкателя равна (рис.6.5) |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
k b (r0 |
|
|
|
S 2 ) , |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Где b- постоянное расстояние от точки N опоры толкателя 2 до оси А |
|||||||||||||||||||||||||||||||||
вращения кулачка; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-наименьший радиус вектор кулачка 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
S2 -перемещение толкателя 2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Имеем |
|
|
|
|
|
|
1 |
|
|
ftg |
|
|
|
|
|
|
1 |
2 |
b |
|
(r0 |
S2 ) |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Из рис. 6.5 получаем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dS2 |
|
|
|
|
|
|
|
|
|
||||||
|
tg |
|
|
|
AP0 |
|
|
|
|
|
|
|
d |
1 |
|
|
|
|
|
|
|
|
|
|
(6.7) |
||||||||
|
|
|
r0 |
S 2 |
|
|
|
|
r0 |
|
|
|
S 2 |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
так как |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
AP0 |
|
|
v2 |
|
|
|
|
|
|
dS2 |
|
|
|
|
|
|
|
|
(6.8) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
||||
Из уравнения (6.7) получаем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
r0 |
|
|
S 2 |
|
dS2 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
d |
1 |
|
|
|
|
tg |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Тогда коэффициент полезного действия |
|
|
|
будет равен |
|
||||||||||||||||||||||||||||
|
|
1 |
f |
|
|
l |
2b |
tg |
|
|
|
2 dS2 |
|
|
|
|
|
(6.9) |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
l |
|
|
|
|
|
|
l d |
1 |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Из равенства (6.9) следует, что коэффициент полезного действия |
|||||||||||||||||||||||||||||||||
уменьшается с увеличением угла давления |
|
|
|
|
. Кулачковый механизм может |
||||||||||||||||||||||||||||
заклиниться, если сила P12 |
P12 cos |
|
|
|
(рис.6.5) |
|
|
будет |
P12 |
F . |
Заклинивание |
||||||||||||||||||||||
произойдѐт, если коэффициент полезного действия |
будет равен нулю. |
||||||||||||||||||||||||||||||||
Тогда из равенства (6.9) получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
f |
|
l |
2b |
tg |
|
|
|
|
|
2 |
|
|
|
|
dS2 |
|
|
|
0 |
|
|
|
|
|
||||||||
|
l |
|
|
|
|
k |
|
|
l |
|
d |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 k |
|
|
|
|
|
|
|
|
|||||||||||
78
k - |
критический |
|
угол, при |
котором |
возникает |
заклинивание |
||||||||||||||||||
механизма, и |
dS2 |
|
- соответствующий этому углу аналог скорости. |
|||||||||||||||||||||
d |
1 1 |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Тогда для критического угла давления |
|
k |
будем иметь: |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
ds2 |
|
|
|
l |
2 f |
dS2 |
|
|
|
|
|||
|
|
|
|
|
tg |
|
|
l |
|
d |
1 |
|
k |
|
|
d 1 |
|
|
|
(6.10) |
||||
|
|
|
|
|
k |
|
f (l 2b) |
l 2b |
|
|
|
|
f (l 2b) |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Из равенства (6.10) следует, что критический угол |
давления k |
|||||||||||||||||||||||
уменьшается с |
увеличением расстояния |
в |
т.е. |
с увеличением |
габаритов |
|||||||||||||||||||
механизма. |
Приближѐнно можно считать, |
что значение |
|
dS2 |
d 1 |
аналога |
||||||||||||||||||
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
||
скоростей, |
соответствующее критическому углу |
k , равно максимальному |
||||||||||||||||||||||
значению этого аналога, т.е.
|
dS2 |
|
dS2 |
|
|
d 1 |
|
d 1 max |
|
Тогда, если заданы размеры механизма и закон движения толкателя, |
||||
можно определить значение критического угла давления k . Необходимо
иметь в виду, что заклинивание механизма обычно имеет место только на фазе подъѐма, соответствующей преодолению полезных сопротивлений, силы инерции толкателя и силы пружины, т.е. когда преодолевается некоторая приведѐнная сила сопротивления T (рис. 6.5). На фазе опускания явление заклинивания не возникает.
Для устранения возможности заклинивания механизма при
проектировании ставят условие, чтобы угол давления |
во всех положениях |
||||||||||
механизма |
был |
меньше |
критического |
угла |
k . |
Если |
максимально |
||||
допустимый угол давления обозначить через |
max , то этот угол должен всегда |
||||||||||
удовлетворять условию |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
max |
k |
|
|
|
(6.11) |
|
на |
практике |
угол давления |
|
max |
для |
кулачковых |
механизмов с |
||||
поступательно движущимся толкателем принимаются |
|
|
|
||||||||
|
|
|
|
max |
300 |
400 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
Для кулачковых механизмов с вращающимся коромыслом, в котором |
|||||||||||
заклинивание является менее возможным, максимальный угол давления |
|||||||||||
|
|
|
max |
450 |
500 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
При проектировании кулачковых можно примять в расчѐтах не угол |
|||||||||||
давления |
, а угол передачи |
12 . Этот угол должен удовлетворять условиям |
|||||||||
|
|
|
12 min |
k , где |
k |
90 |
k |
|
|
||
79
6.4. Определение угла давления 
через основные параметры кулачкового механизма
Угол давления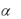 
может быть выражен через основные параметры кулачкового механизма. Для этого рассмотрим кулачковый механизм (рис.6.4) с поступательно движущимся толкателем 2. Проводим в т. B2 нормаль n n и находим мгновенный центр вращения P0 в относительном
движении звеньев 1 и 2. Из dB2 P0 |
|
имеем: |
|
|
|
|
|
|
|
|
||||||||||
|
tg |
(dP0 ) |
|
|
( AP0 ) ( Ad ) |
|
|
|
(6.12) |
|||||||||||
|
(dB2 ) |
|
|
(dc) (cB2 ) |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||
Согласно равенству (6.8) |
|
AP0 |
|
|
dS2 |
2 1 , Ad |
l , где |
l - |
кратчайшее |
|||||||||||
|
|
|
d |
|
1 |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
расстояние |
от оси А кулачка |
|
до |
|
оси толкателя, |
dc |
r 2 |
l 2 , где r - |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
минимальный радиус вектор кулачка и |
|
CB2 |
S2 , где, |
заданное его законом |
||||||||||||||||
движения S2 |
S2 ( 1 ) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Подставляя указанные параметры в равенство (6.12), получаем |
||||||||||||||||||||
|
|
|
|
|
|
dS2 |
|
l |
|
|
|
|
|
|
|
|
|
|||
|
tg |
|
|
|
|
d |
1 |
|
|
|
|
|
|
|
|
|
(6.13) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
r |
2 |
l 2 |
S |
2 |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Знак “+” у кратчайшего расстояния l |
соответствует левому от оси А |
|||||||||||||||||||
его расположению, знак "-" - правому (6.4) при условии, что толкатель движется вверх, а кулачок вращается против часовой стрелки.
Из равенства (6.13) следует, что при выбранном |
законе движения |
|||
S2 S2 ( 1 ) |
и размере l габариты кулачка определяются |
радиусом r0 , |
мы |
|
получаем |
меньшие углы давления , |
но большие габариты кулачкового |
||
механизма. |
|
|
|
|
И наоборот, если уменьшить r0 , |
то возрастают углы давления |
и |
||
уменьшается коэффициент полезного действия механизма. Если в механизме (рис.6.5) ось движения толкателя проходит через ось вращения кулачка и l 0 , то равенство (6.13) примет вид
|
|
dS2 |
|
|
|||
tg |
|
d |
1 |
|
|
(6.14) |
|
r0 |
S |
2 |
|||||
|
|
||||||
80