2937

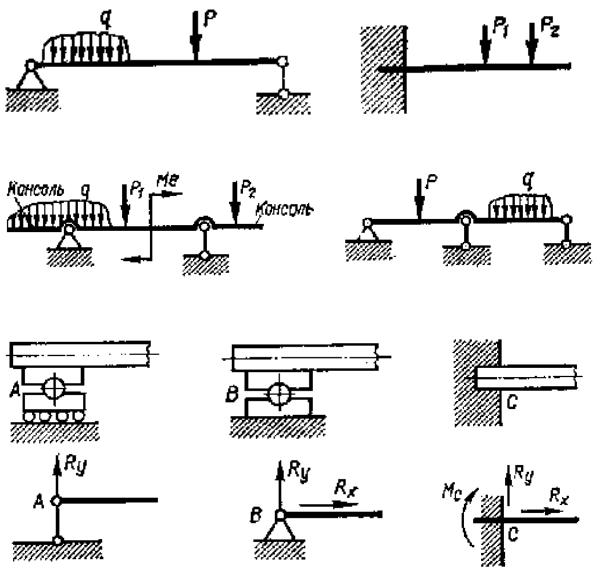
Глава 5. ИЗГИБ

5.1. Типы брусьев и опор

Плоский изгиб. Рассмотрим брус цилиндрической или призматической формы с прямолинейной осью. Брус испытывает плоский изгиб, если силы и моменты, изгибающие брус, расположены в плоскости, проходящей через его продольную ось и содержащей одну из главных центральных осей инерции сечения.

Горизонтальный брус, закрепленный на опорах и испытывающий деформацию изгиба, называется балкой. Различают статически определимые и статически неопределимые брусья. Встречают три типа статически определимых брусьев: шарнирно опертый (рис. 5.1,а), консольный (рис. 5.1,б) и консоль (рис. 5.1,в). На рис. 5.1,г показан сложный статически неопределимый двухпролетный брус.

Рис. 5.1. Расчетные схемы и опорные закрепления брусьев при их изгибе

41

Опорные реакции. Различают три основных типа опор:1) шарнирно-подвижная опора А (рис. 5.1,д) может воспринимать вертикальную нагрузку и на ней, следовательно, возникает только вертикальная реакция; 2) шарнирно-неподвижная опора В (рис. 5.1,е) может воспринимать как горизонтальные, так и вертикальные усилия; 3) жесткое защемление С (рис. 5.1,ж) воспринимает вертикальную и горизонтальную нагрузки, а также моментную нагрузку.

Под действием внешних нагрузок в местах закрепления бруса возникают опорные реакции. Для определения опорных реакций в статически определимом брусе достаточно составить три уравнения статики. Введем обозначения: P - сосредоточенная сила; q - интенсивность распределенной нагрузки; M e - сосредоточенный момент внешних сил (рис.5.1,б). При

отыскании опорных реакций распределенную нагрузку q заменяют равнодействующей сосредоточенной силой. Для статически неопределимого бруса также можно записать три уравнения статики, однако их число окажется меньше числа разыскиваемых опорных реакций. Поэтому при отыскании опорных реакций в статически неопределимом брусе необходимо составить уравнения совместности деформаций, дополняющее уравнения статики.

5.2. Эпюры поперечных сил и изгибающих моментов

Изгибающий момент. Рассмотрим брус (рис. 5.2,а), находящийся в равновесии под действием четырех сил, каждая из которых равна P. Исследуем внутренние силы упругости, действующие по произвольному сечению m – m на участке ВС.

Применим метод сечений. Если пренебречь силами веса, то уравнения равновесия для части бруса, лежащей слева от сечения m – m (рис.5.2,б), запишутся в виде:

соответственно; M z - момент внутренних сил упругости, действующих по сечению m – m со

стороны правой части бруса на левую.

Из третьего уравнения системы (5.1) следует, что внутренние силы упругости, действующие по поперечному сечению, расположенному на участке ВС, должны сводиться к моменту , равному по величине моменту Pa внешних сил, действующих по одну сторону от рассматриваемого сечения. Момент внутренних сил упругости относительно оси Oz (нейтральная ось), проходящей через центр тяжести рассматриваемого сечения, численно равный моменту внешних сил, приложенных к брусу по одну сторону от данного сечения относительно той же оси, называется изгибающим моментом. Таким образом, на участке ВС изгибающие моменты, действующие в различных сечениях, численно равны одному и тому же значению Pa. Нагружение бруса двумя равными моментами, действующими в одной центральной плоскости и приложенными по концам его, называется чистым изгибом.

Поперечная сила. Иное положение на участках бруса АВ и СD. Проведем сечение n –n на участке АВ. На часть бруса, лежащую слева от этого сечения, со стороны правой части действуют внутренние силы упругости, которые, как известно, сводятся к изгибающему

42

Построение эпюр. Графики изменения поперечных сил и изгибающих моментов вдоль центральной оси бруса называются эпюрами. При построении эпюр поперечных сил и изгибающих моментов в большинстве случаев следует начинать с определения реакций опор.

Рис. 5.3. Правило знаков для изгибающего момента и поперечной силы

Определив реакции, брус следует разбить на участки, на протяжении которых нагрузка однородна. Для каждого участка составляют общие выражения для поперечной силы и изгибающего момента, для чего рассматривают произвольное сечение в пределах данного участка и строят эпюры, давая аргументу х произвольные значения в пределах того же участка.

Порядок построения эпюр рассмотрим на примере шарнирно опертого бруса, нагруженного сосредоточенной силой (рис. 5.4,а). Из уравнения равновесия бруса:

M (z) B RA L Pb 0

находим реакцию на левой опоре:

RA PLb .

Из второго уравнения равновесия найдем реакцию на правой опоре:

RB PLa .

Брус содержит два участка (AC и CB ) с однородной нагрузкой. На первом участке АС общие выражения для поперечной силы и изгибающего момента следующие:

границе участка в точке С.

На втором участке СВ общие выражения для произвольно взятого поперечного сечения:

44

т.е. поперечная сила имеет постоянное значение, а изгибающий момент убывает по линейному закону от M (a) P bL a в начале участка (точка С) до нуля (в точке В при x=L).

Следовательно, эпюра поперечной силы (рис. 5.4,б) на границе участков в точке, где приложена сосредоточенная сила P, имеет скачок на величину P, т.е. функция Q(х) терпит разрыв первого рода. Изгибающий момент М(x) на первом участке увеличивается, а на втором уменьшается (рис. 5.4,в). В точке приложения сосредоточенной силы эпюра изгибающего

момента имеет излом. Иначе говоря, производная dM (x) претерпевает разрыв в точке С. dx

а)

б)

45

б)

в)

Рис. 5.5. Схема нагружения и эпюры поперечной силы и изгибающего момента консоли

5.3. Основные дифференциальные зависимости при изгибе

Связь между изгибающим моментом и поперечной силой. Рассмотрим поперечный изгиб бруса, загруженного сосредоточенной силой (рис. 5.4). В сечении, взятом на расстоянии х от левой опоры, в пределах второго участка действует поперечная сила:

47

Связь между поперечно силой и распределенной нагрузкой. Пусть у бруса АВ с распределенной нагрузкой интенсивности q(x) (рис. 5.6) поперечная сила в произвольном сечении, взятом на расстоянии х от левого конца бруса, равна Qy . Тогда в сечении с абсциссой

x+dx поперечная сила равна Qy dQy . Так как dQy q(x)dx, то:

Если продифференцировать по х равенство (5.5), то с учетом уравнения (5.6) получим:

Уравнения (5.5), (5.6) и (5.7) являются основными дифференциальными зависимостями при изгибе. Эти зависимости можно использовать в качестве средства контроля при построении эпюр поперечных сил и изгибающих моментов.

Рис. 5.6. К изгибу бруса распределенной нагрузкой произвольной интенсивности

5.4. Нормальные напряжения при чистом изгибе

Деформации. Брус постоянного поперечного сечения (рис. 5.7,а) нагрузим внешними моментами M e , приложенными к торцам. Под их действием брус изогнется: его верхние

волокна укоротятся, а нижние удлинятся (рис. 5.7,б). В средней по высоте части бруса находится слой волокон, который не будет изменять свою длину,- нейтральный. Положение этого слоя NN заранее неизвестно. Линия пересечения нейтрального слоя с поперечным сечением бруса называется нейтральной осью или линией.

При изгибе справедлива гипотеза плоских сечений Бернулли: сечения, бывшие плоскими до деформации, остаются плоскими и после деформации и лишь поворачиваются относительно соответствующих нейтральных линий.

Плоскостями, перпендикулярными к оси Ox, выделим элемент бруса длиной dx и рассмотрим волокно n - n, расположенное в нейтральной плоскости, и волокно m – m на

расстоянии y0 от n - n. До деформации mm nn dx. В процессе деформации сечения ab и a1b1 повернутся одно относительно другого на некоторый угол d . Если радиус кривизны

После деформации волокно n - n сохранит свою длину неизменной: nn dx d ,

а волокно m - m удлинится:

48

mm ( y0 )d .

Абсолютное удлинение волокна m - m:

dx ( y0 )d d y0 d .

Относительное удлинение этого волокна:

x d

а)

б)

в)

Рис.5.7. Напряжения при чистом изгибе

49

являющаяся проекцией на плоскость сечения главного вектора внутренних сил упругости, действующих по сечению, при чистом изгибе равна нулю и, принимая во внимание, что сила, лежащая в плоскости сечения, не может дать момента относительно любой оси, лежащей в этой

рассмотрении чистого изгиба не учитывается. Запишем уравнения равновесия для правой части бруса:

( F )

где y0 - расстояние от центра тяжести площадки до оси. Первое из уравнений (5.9) дает:

через центр тяжести сечения. Статический момент сечения относительно любой другой оси (не центральной) не равен нулю.

В соответствии со вторым уравнением (5.9) внешний момент оказывается равным изгибающему моменту от действия нормальных напряжений:

( F )

50