2685

Рис. 4.11. Условныеобозначения при анализе надежности методом замкнутых контуров

Топология структурной схемы надежности отображается в матрице инцидентности контуров и ветвей В, элементы которой brv, 1≤r≤m, 1≤v≤n определяются следующим образом:

Элементы mrr’ квадратной матрицы контурных разделений М порядка m определяются следующим образом: mrr’=(М) rr’(r, r’=1,…, m) представляет собой функцию отказа прямого разделения r-го и r’-го замкнутых контуров. Таким образом, для диагональных элементов mrr=1(r=1,…, m) в то время, как остальные элементы mrr’(r≠r’, r=1,…, m) определяются булевой суммой функций отказа всех ветвей, прямо разделяющих r-й и r’-й замкнутые контуры.

Если в диагональной матрице Х порядка n (матрица отказов ветвей) объединяют функции отказов отдельных ветвей X=<x1,x2,…,xn>, то

M=I˅B˄XBT, (4.49)

Доказательство этой формулы можно провести так же, как и формулы в предыдущем пункте. В частности, при r≠r’

91

в соответствии с определением матрицы М.

Теорема 3 [52]. Элемент (M(i) rr’) (r, r’=1,…, m) i-й степени булевой матрицы контурных разделений М представляет собой функцию отказа всех разделяющих сечений между контурами r и r’, проходящих через любые другие замкнутые контуры, число которых 0, 1, …, i-1.

Теорема 4 [52]. Элемент матрицы (M(m-1)) m-1, m представляет собой функцию отказа рассматриваемой структурной схемы надежности. Если при выполнении булева умножения матриц последовательно опускать булевы выражения, соответствующие разделяющим сечениям, которые многократно встречаются по меньшей мере у одного замкнутого контура, то получим функцию отказа в виде, соответствующем представлению функции работоспособности системы как параллельного соединения эквивалентных схем дополнений минимальных сечений (по работоспособности) между (m-1)-м и m-м контурами.

В качестве примера рассмотрим представленную на рисунке 4.12 структурную схему надежности с обозначенными замкнутыми контурами и ветвями.

Рис. 4.12. Эквивалентная схема по отказу с обозначенными ветвями и контурами

92

Из матрицы отказов ветвей X=(x1,x2, x3,x4, x5,x6, x7,x8) и матрицы инцидентности замкнутых контуров и ветвей

получаем матрицу контурных разделений M=I˅B˄XBT, имеющую вид

которую можно построить, исходя непосредственно из структурной схемы надежности. Опуская промежуточные расчеты, приходим к следующему результату:

S(x)=(M(5))56=12˅78˅1367˅2345˅2368˅4567

или S(x)=(1˅2)˄(7˅8) ˄(1˅3˅6˅7) ˄(2˅3˅4˅5) ˄(2˅3˅6˅8) ˄(4˅5˅6˅7).

В противоположность методу узлов метод замкнутых контуров позволяет проанализировать непосредственно лишь те структурные схемы надежности, граф которых является плоским. Если все же хотят применить метод замкнутых контуров для неплоских графов, то предварительно

93

необходимо сделать переход, приводящий к плоским графам с помощью формулы приведения:

S(x1, …, xi-1, xi, xi+1,…, xn)= xiS(x1, …, xi-1, 0, xi+1,…, xn)+ xiS(x1, …, xi-1, 1, xi+1,…, xn)= xiS1(x1, …, xi-1, xi+1,…, xn)+ xiS2(x1,

Формулу (4.51) применяют для того, чтобы избавиться от пересечений ветвей неплоского графа, которые не удается устранить непрерывными преобразованиями типа «изгиб ветвей».

Рис. 4.13. Пятиугольник как пример неплоского графа

Рис. 4.14. Другое представление графа на (рис. 4.13).

94

У графа с одним существенным пересечением ветвей можно с помощью теоремы приведения удалить одну из тех ветвей, которые обусловливают это пересечение, и таким образом от неплоского графа перейти к 2 плоским графам с (n- 1)-й ветвью. Неплоские графы с k существенными пересечениями также можно преобразовать многократным применением теоремы приведения в плоские графы.

В качестве примера проанализируем методом замкнутых контуров схему надежности, приведенную на рисунке 4.13.

Очевидно, что ветви графа можно изогнуть так, что из 5 точек пересечения останется лишь одна, например, пересечение ветвей 4 и 5 (рис. 4.14).

Для определения всех минимальных сечений можно представить функцию отказа, согласно уравнению (4.51), следующим образом:

S(x1, …, x10)= x5S1(x1, …, x4, x6,…, x10)+ x5S2(x1, …, x4,

плоскими, их структура представлена на (рис. 4.15.).

Рис. 4.15. Плоские графы, получающиеся из пятиугольника (а - ветвь 5 заведомо не функционирует, б –

ветвь 5 заведомо функционирует).

95

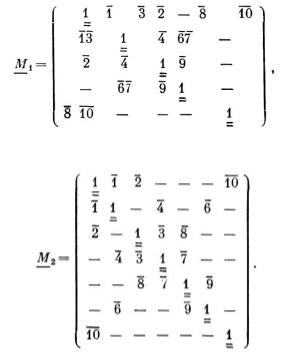
Матрицы контурных разделений М1 и М2 обоих графов при выбранных обозначениях замкнутых контуров имеют вид

Отсюда после несложных преобразований находим минимальные сечения и тем самым функцию отказа подсистем

S1=(M1(4))45=28910˅2467810˅1348910˅1367810, S2=(M2(6))67=1610˅28910˅234610˅1348910˅146910˅23791

0˅2467810.

Теперь функцию отказа всей системы

S(x)=15610˅28910˅1348910˅2467810˅1367810˅1457910˅

2345610˅2357910.

96

Структурная схема надежности, представленная на (рис. 4.13), эквивалентна последовательному соединению дополнений минимальных сечений. Последовательнопараллельная система, представленная на (рис. 4.16), имеет одинаковую функцию работоспособности, как и эквивалентная схема 4.13.

Рис. 4.16. Последовательно-параллельная система

97

5. РИСК-МОДЕЛИ ОЦЕНКИ ЖИВУЧЕСТИ ИНФОРМАЦИОННО-ТЕЛЕКОММУНИКАЦИОННЫХ

СЕТЕЙ

5.1.Теоретические основы риск-анализа живучести

Вэтом разделе мы будем исходить из того, что изделие в момент времени t = 0 является заведомо работоспособным. (Моментом t = 0 можно считать, например, момент продажи изделия изготовителем, момент истечения гарантийного срока обслуживания и т. д.) Через некоторое время t >0 может произойти отказ изделия, хотя условия для функционирования изделия остаются допустимыми. Мы рассматриваем поведение изделия от момента временя t = 0 до момента его первого отказа. Ни само изделие, ни его отдельные части в это время не должны ремонтироваться, заменяться новыми (или бывшими в эксплуатации). Такие условия функционирования изделия собственно и определяют понятие «изделие без восстановления» (или «невосстанавливаемое изделие») [47 - 49].

Интервал времени от t= 0 до момента t первого отказа назовем наработкой рассматриваемого изделия. Для отдельно выбранного из однородной партии (с одинаковыми условиями изготовления, транспортировки и т, д.) изделия нельзя точно предсказать момент отказа. Случайные факторы, воздействия которых не удается избежать в условиях производства (при фиксированном допустимом уровне затрат, транспортировки и т. д.), сказываются на величине наработки отдельного изделия. Поэтому наработки у совокупности одинаковых изделий есть случайные величины и естественно, что количественное описание процесса функционирования изделий опирается на аппарат теории вероятностей и математической статистики. Такой подход сегодня является общепринятым.

Случайную длительность наработки обозначим T. Её реализации являются неотрицательными числами. Распределение Случайной величины T можно задать, например, с помощью функции распределения

98

В большинстве случаев под T Понимается непрерывная случайная величина, для которой существует плотность распределения

Если наработка Е зависит только от числа циклов включения, то является дискретной случайной величиной.

Функция распределения FT, дополнительная функция RT и плотность распределения fT – каждая однозначно характеризует распределениявероятностей непрерывной случайной величины

T [47 - 49].

Часто возникает вопрос об оценке вероятности отказа в интервале времени (t, t+dt) для изделий которые время t уже отработали. Для этого определяют величину λT(t)dt как вероятность того , что неотказавшие до момента t изделия откажут в интервале (t, t +dt), т.е.

Функция λ (t) называется интенсивностью отказов. Она позволяет особенно отчетливо выявлять различия между типами распределения вероятностей. Так, для важнейших распределений наработок (распределения Вейбулла, логарифмически-нормального распределения и гаммараспределения) эти различия при надлежащем выборе параметров распределения проявляются лишь на «концах» самих функций распределения, т, е, при t→∞. График соответствующих плотностей распределения fT вообще не дает

99

заметной разницы. В то же время различие ясно видно по графику интенсивностей отказов [47 - 49].

Иногда нас интересует также функция rT (t), представляющая собой ожидаемую остаточную наработку для изделия, которое безотказно уже отработало время t, Очевидно, эта характеристика относится лишь к таким изделиям, которые до момента времени t не отказали. Распределение наработки этих изделий можно получить из первоначального распределения наработок. Рассмотрим для этого рис. 5.1, где штриховой линией показана возможная плотность распределения наработки fT (х)> Точный ход этой плотности распределения до момента времени t для нас неважен. Часть изделий, которая откажет после момента времени t, опреде-

лится как

∞

Рис. 5.1.Плотность распределения наработки fT(x) и плотность распределения остаточной наработки kT (t, x) для

момента времени t.

Так как для ожидаемой остаточной наработки важна лишь эта часть изделий, то соответствующая плотность распределения определиться следующим образом:

100