2394

где dz - приращение длины продольного элемента, имевшего до нагружения длину dz .

Следовательно, абсолютное удлинение стержня равно

где - длина стержня. Если напряжение ζ не изменяется по длине, то

Это выражение часто называют обобщенным законом Гука при растяжении и сжатии.

2.2.2. Пример [2]

Определим удлинение стержня длиной с постоянным поперечным сечением площадью F (рис. 2.2) под действием собственного веса. Пусть модуль упругости материала равен Е, а удельный вес . Нормальная сила в сечении, удаленном

на z от нижнего конца стержня, равно

N Fz

Следовательно, напряжение в этом сечении

N 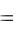z .

F

Как видим, оно не зависит от площади поперечного сечения.

2.2.3. Поперечная деформация На рис. 2.3 схематично показан стержень до приложения

растягивающей нагрузки (сплошная линия) и после приложения нагрузки (пунктирная линия). Как видно из рисунка, и это соответствует наблюдениям, при растяжении наряду с удлинением происходит уменьшение размеров в поперечном направлении. и, аналогично, при сжатии стержня наряду с его укорочением наблюдается возрастание поперечных размеров. Это изменение размеров поперечного сечения при растяжении и сжатии характеризуется поперечной деформацией εn. Как по-

казали экспериментальные исследования, поперечная деформация у стержней из изотропного материала одинакова в разных направлениях в плоскости поперечного сечения и пропорциональна продольной деформации:

n ,

где - константа материала, называемая коэффициентом Пу-

ассона и изменяющаяся в пределах от 0 до 0,5. У сталей

0,3.

2.3. Статически неопределимые стержневые системы К статически неопределимым относят стержневые систе-

мы, у которых число неизвестных усилий превышает число независимых уравнений равновесия. Различного рода статически неопределимые стержневые системы широко применяются на практике, поскольку они обычно имеют большую жесткость и устойчивость.

Разность чисел неизвестных усилий и независимых уравнений равновесия называют степенью статической неопределимости системы. Аппаратом теоретической механики нельзя определить усилие в стержнях таких систем.

Эту задачу можно решить, если учесть деформируемость стержней. Начнем с рассмотрения примера.

2.3.1. Пример На рис. 2.4 показана система трех стержней, нагруженных

заданной силой Р. Для определения трех неизвестных внутренних усилий в стержнях располагаем двумя независимыми уравнениями равновесия (поскольку имеем плоскую систему сходящихся сил). Следовательно, степень статической неопределимости системы равна единице (или, как говорят, система однажды статически неопределима). Если добавить к этой системе еще один стержень система станет дважды статически неопределимой и т.д. Если убрать любой из показанных на рисунке стержней система станет статически определимой.

Рис. 2.2

Рис. 2.3

Определим внутренние усилия в стержнях в случае симметричной конструкции, когда площади поперечных сечений и материал крайних стержней

одинаковы. Будем все величины, относящиеся к этим стержням, обозначать с индексом I, а все величины, относящиеся к среднему стержню - с индексом 2.

На узел А действует система сил, показанных на рис.2.5. Эта система должна удовлетворять двум независимым уравнениям равновесия, каковыми могут служить равенства нулю сумм проекций всех сил на координатные оси x, y. Первое равенство отождествляется следствие симметрии системы, вто-

Как видим, внутренние усилия нельзя определить из уравнений равновесия.

Рассмотрим деформацию стержневой системы. Под действием силы Р стержни растянутся, узел А опустится и займет положение А1 (рис. 2.6) . Абсолютное удлинение стержня 2 равно отрезку АА1. Для определения абсолютного удлинения стержня I следовало бы провести через точку А дугу окружности с центром в точке 0. Отрезок, отсекаемый этой дугой от отрезка ОА1 , будет равен разности длин стержня I после и до нагружения и, следовательно, равен абсолютному удлинению этого стержня. Однако вследствие малости деформаций стержней дугу окружности можно заменить отрезком касательной, т.е. перпендикуляром АВ , опущенным из точки А на отрезок OA1. В результате получаем абсолютное удлинение стержня 2 равным отрезку BA1.

Далее замечаем, что между удлинениями стержней I и 2 существует простая связь

Здесь в силу малости деформаций стержней мы не делаем различия в угле между стержнями I и 2 до и после нагружения, что соответствует принятому ранее принципу начальных размеров.

Рис. 2.6

Ри

Таким образом, из рассмотрения деформации стержневой системы следует уравнение (2.2), связывающее между собой удлинения стержней, называемое уравнением совме-

стности деформации. Если к стержням рассматриваемой системы добавить два симметрично расположенных

стержня, то получим дважды статически неопределимую систему. Легко увидеть, что вдобавок к уравнению (2) в этом случае можно записать аналогичное уравнение, связывающее удлинение стержня 2 и добавляемых стержней. Таким образом, число независимых уравнений совместности деформаций соответствует степени статической неоп-

ределимости стержневой системы. По закону Гука

Знак " + " при внутренней силе указывает на то, что сила действительно имеет направление, показанное на рис. 2.5. Если бы ответ был получен со знаком "-", то это означало бы, что направление соответствующей силы является противоположным. Обычно имеется произвол в выборе направлений внутренних сил при использовании метода сечений. Следует только иметь в виду, что направление этих сил (рис. 2.5) должно соответствовать деформациям стержней (рис. 2.6), т.е. если стержень удлиняется, то внутреннее усилие в нем должно быть растягивающим, т.е. направленным от сечения. Если стержень укорачивается, то сила должна быть сжимающей.

Произведение ЕF обычно называют жесткостью при растяжении (сжатии). Как видим, для определения внутренних усилий в стержнях статически неопределимой системы необходимо знать соотношение жесткостей стержней этой системы.

При прочих равных условиях внутреннее усилие стержня тем больше, чем больше его жесткость.

Если требуется подобрать площади поперечных сечений стержней, то используют условие прочности:

Легко убедиться, что в общем случае нельзя удовлетворить этим двум условиям, взятым со знаком равенства. Действительно, если они взяты со знаком равенства, то из (4) получаем

Отсюда следует, что равнопрочность стержней статически неопределимых систем (когда отношение напряжений в стержнях к соответствующим допускаемым напряжениям одинаково) достижимо лишь в сугубо частных случаях.

Обычно при решении такого рода задач при известных модулях упругости материала стержней задается соотношение площадей их поперечных сечений. Тогда величины этих площадей можно определить из условий прочности. Пусть в рас-

Найдем по (2.5) внутренние силы и из первого условия (2.6), взятого со знаком равенства, найдем F2 . Далее найдем F2=kF1 и проверим, удовлетворяет ли эта площадь второму неравенству (2.6). Если удовлетворяет, то задача решена, если нет, то необходимо F2 определить из этого неравенства, а F1

принять равной F2\k .

2.3.2. Монтажные напряжения Монтажными называют напряжения, возникающие при

сборке статически неопределимых стержневых систем вследствие неточности изготовления их элементов. Легко убедиться в том, что в статически определимых системах монтажные напряжения не возникают. Рассмотрим, например, конструкцию,

показанную на рис. 2.7. Пусть длина стержня I несколько больше проектной. Это приведет лишь к тому, что конструкция несколько исказится (пунктир на рис. 2.6), но напряжения при этом не возникнут.

Обратимся теперь к статически неопределимой системе

(рис. 2.8). Пусть длина стержня 2 меньше проектной на величину . Для того, чтобы собрать конструкцию необхо-

димо стержень 2 растянуть и соответственно сжать стержни I. В результате возникнут монтажные напряжения. Понятно, что задача определения монтажных напряжений является статически неопределимой. Ограничившись рассмотрением симметричной конструкции, будем решать эту задачу также, как решали предыдущую . Вырезав узел А смонтированной конструкции, расставив действующие на него силы (рис. 2.9) и запишем уравнение равновесия

-2N1cosβ+N2=0. (2.7)

Далее рассматриваем деформацию стержневой системы. Легко увидеть, что между деформациями стержней существует следующая связь

Далее по закону Гука имеем

(Здесь учтена малость δ по сравнению с ). Подставим (2.9) в (2.8), получаем

Решая систему уравнений (2.7), (2.10), можем определить внутренние силы, а затем и монтажные напряжения. Заметим,

что монтажные напряжения определяются не абсолютной (δ),

Возникновение монтажных напряжений является недостатком статически неопределимых систем. Однако этот недостаток можно обратить и в достоинство, если точность изготовления стержней является контролируемой. Так, рассмотренная выше стержневая система, нагруженная силой P (рис . 2.4), при точном изготовлении стержней и одинаковой их жесткости ЕF является неравнопрочной - средний стержень является более нагруженным, чем крайние. Если средний стержень

изготовить более длинным ( 1= 2/cosβ+δ) , то при сборке конструкции в нем возникнут сжимающие напряжения, а в крайних – растягивающие. При нагружении этой конструкции силой Р и при изменении δ в определенных пределах распределение напряжений в стержнях будет более равномерным .

2.3.3. Температурные напряжения

Температурными называются напряжения, возникающие в статических неопределимых стержневых системах при изменение температуры всех или отдельных стержней этой системы.

Обратимся опять к системе трех стержней, показанной на рис. 2.10 . Если нагреть стержень 2 на ∆Т0, то возникает температурное удлинение этого стержня

где -коэффициент температурного расширения материала. Этому удлинению препятствуют крайние стержни. В результате стержень 2 окажется сжатым, а стержни I - растянутыми, возникнут температурные напряжения. В статически определимых системах температурные напряжения не возникают. В этом можно убедиться на примере конструкции, показанной на рис. 2.7. Изменение температуры любого из стержней этой

системы или обоих стержней одновременно будет приводить лишь к некоторому перемещению узла А и не будет вызывать какие-либо напряжения в стержнях.

Определим, например, напряжения возникающие в стержнях показанной на рис. 2.10 симметричной конст-

рукции при ее нагреве на ∆t0 .

На рис. 2.11 показаны силы, действующие на узел А. Записываем уравнение равновесия

N2+2N1cosβ=0. (2.11)

Уравнение совместности деформаций по-прежнему имеет вид

Однако в данном случае необходимо учесть, что удлинение складывается из удлинения, связанного с внутренним усилием, и температурного удлинения

В связи с тем, что на рис. 2.11 все внутренние усилия в стержнях показаны растягивающими, удлинения, связанные с внут-

(2.13) положительными.

Подставив равенство (2.13) в уравнение (2.12), получим уравнение относительно внутренних сил. Решая его совместно с (2.11), находим внутренние силы, а затем температурные напряжения.