2394

Как видим, рассматриваемый интеграл равен произведению площади первой эпюры на ординату второй эпюры в точке с координатой центра тяжести первой эпюры.

Если обе функции f1 и f2 линейные, то операция их «перемножения» обладает свойством коммутативности. В этом случае безразлично, умножается ли площадь первой эпюры на ординату второй или наоборот.

Способ Верещагина применим ко всем шести интегралам Мора. Упрощение, достигаемое при использовании способа Верещагина, обусловлено тем, что эпюры внутренних силовых факторов можно обычно разбить на простейшие фигуры: треугольник, прямоугольник и параболический треугольник. Определение площади и положения центра тяжести треугольника и прямоугольника общеизвестно. На рис. 6.8 приведена формула для определения площади и показано положение центра тяжести параболического треугольника.

Рис. 6.8

Способом Верещагина можно, например, определять перемещения при изгибе прямых балок. Пренебрегая влиянием поперечной силы, получим в случае прямого изгиба

Здесь i – номер определяемого перемещения. Суммирование производится по всем участкам (в пределах каждого уча-

стка должны быть регулярны и эпюра изгибающих моментов от заданной нагрузки, и эпюра изгибающего момента от единичной силы), а случае «расслаивания» эпюры на некоторых участках на простейшие элементы (треугольники, прямоугольники и т.д.), то и по всем этим элементам. Формула остается одинаковой и при определении прогиба, и при определении поворота сечения. Только в первом случае Mik – изгибающий момент от единичной силы, а во втором случае – от единичного момента.

Пример. Определим прогиб в точке А балки, показанной на рис. 6.9. Для этого построим эпюру изгибающих моментов от нагрузок на балку, а также от единичной силы приложенной в точке А.

Рис. 6.9

На участке ВС площадь эпюры моментов от нагрузки равна Pl2/2, а момент от единичной силы под центром тяжести этой части эпюры равен l/3

На участке АВ площадь эпюры моментов от нагрузок равна Pl2/2, а момент от единичной силы под центром тяжести эпюры от нагрузок равен 5l/8.

Учитывая симметрию рассматриваемых эпюр, запишем

Ответ получен положительным. Это значит, что прогиб происходит в направлении единичной силы, т.е. вниз.

6.3.Раскрытие статической неопределимости стержневых систем методом сил

6.3.1. Степень статической неопределимости Под стержневой системой понимают конструкцию, со-

стоящую из элементов, имеющих форму стержня. Если элементы такой конструкции работают в основном на растяжение или сжатие, то еѐ называют фермой. Ферма состоит из прямых шарнирно соединѐнных стержней. Нагрузки на ферму прикладываются к еѐ узлам.

Если хотя бы некоторые из элементов стержневой системы работают в основном на изгиб или кручение, такую систему называют рамой. Раму (или ферму), у которой оси всех составляющих элементов и действующие на них силы расположены в одной плоскости, называют плоской.

Рамы и фермы делят на статически определимые и на статически неопределимые. Под статически определимой понимают такую кинематически неизменяемую систему, для которой при заданных нагрузках можно из уравнений равновесия, записанных для всей конструкции или для отдельных еѐ частей, выделенных методом сечений, определить все реакции опор и внутренние силы в стержнях. Если же такое определение реакций опор и внутренних сил невозможно, стержневую систему называют статически неопределимой.

Разность между числом неизвестных реакций опор и внутренних усилий и независимых уравнений равновесия называется степенью статической неопределимости. Степень статической неопределимости может определяться как число ―дополнительных‖ связей, наложенных на систему. Под дополнительными понимают связи, наложенные на систему сверх необходимых для обеспечения кинематической неизменяемости. Поясним это на примерах.

Балка, защемлѐнная одним своим концом (рис. 6.10, а) является кинематически неизменяемой системой (это означает, что приложение к ней не очень больших нагрузок приводит

лишь к малым перемещениям, обусловленным деформацией балки). Любая дополнительная опора накладывает на балку дополнительные связи (шарнирно подвижная опора – одну, шарнирно неподвижная – две и т.д.). У балки, изображенной на рис. 6.10, б две такие дополнительные связи, следовательно, степень еѐ статической неопределимости равна двум.

Рис. 6.10

Связи, ограничивающие перемещения конструкции как жесткого целого, называют внешними. В рассмотренном примере речь шла о внешних связях.

Связи, ограничивающие взаимные смещения отдельных элементов конструкции, называют внутренними.

Рассмотрим пример иллюстрируемый на рис. 6.11. На рисунке показана статически определимая рама. При любых нагрузках реакции опор и внутренние силы в стержнях этой рамы можно определить из уравнений равновесия. Ясно, что рама является кинематически неизменяемой, следовательно, имеются необходимые связи. Если же соединить стержни 1 и 2 в узле А (рис. 6.8, б), то тем самым окажутся ограниченными взаимные смещения этих стержней, т.е. будут наложены дополнительные внутренние связи. Система станет статически неопределимой. Если соединение шарнирное, то оно ограничит линейные перемещения сечения А стержня 1 относительно сечения А стержня 2, т.е. будут наложены две дополнительные внешние связи. Если соединение в узле А неподвижное, то наложено три дополнительные связи. В связи с этим заметим,

что замкнутый внешний контур имеет три дополнительные связи и в силу этого трижды статически неопределим.

Рис. 6.11

Приведѐм несколько примеров к определению степени статической неопределимости (рис. 6.12):

а) кольцо имеет три внутренние дополнительные связи, и поэтому трижды статически неопределимо;

б) рама имеет три дополнительные внешние и три дополнительные внутренние связи. Степень статической неопределимости – шесть;

в) на раму наложены одна внешняя дополнительная связь и две внутренние. Степень статической неопределимости – три.

6.3.2. Метод сил Метод заключается в следующем. Рассматриваемая стати-

чески неопределимая система освобождается от дополнительных связей. Действие этих связей заменяется неизвестными силами и моментами. Их величина находится решением системы уравнений, согласно которым перемещения в стержневой системе соответствуют тем ограничениям, которые накладываются на неѐ отброшенными связями.

Рис. 6.12

Стержневая система, освобождѐнная от дополнительных связей и в силу этого становящаяся статически определимой, называется основной системой.

Для каждой статически неопределимой системы можно подобрать множество различных основных систем. На рис. 6.13 приведены четыре основные системы для показанной на этом рисунке плоской рамы. Все они удовлетворяют требованиям к основной системе – все являются статически определимыми.

Рис. 6.13

Выберем для дальнейшего анализа расчѐтную схему, изображѐнную на рис. 6.13,б. В данном случае рама освобождена от трѐх связей, запрещающих два линейных (вдоль координатных осей) и угловое перемещение сечения А (рис. 6.14).

Рис. 6.14

Заменим действие этих связей их реакциями Х1, Х2, Х3. Здесь Х1, Х2 – силы, а Х3 – момент. Основная система будет эквивалентна рассчитываемой раме, если эти реакции будут такими по величине, что соответствующие им перемещения сечения А обратятся в нуль, т.е. если

В соответствии с принципом независимости действия сил можем записать

сечения А в направлении силы (или момента) xi , под дейст-

вием силы (или момента) x j , а ip - перемещение сечения А

в направлении силы (или момента) xi под действием всех

приложенных к раме нагрузок (в данном случае они представлены только моментом М). Поскольку предполагается справедливым закон Гука, можем записать

i x j ij x j ,

где ij - перемещение точки приложения силы xi в направлении этой силы под действием единичной силы, направленной

вдоль x j . Таким образом, уравнение (6.10) можно переписать в виде

3

j 1

Ясно, что таким же образом можно получить аналогичные уравнения и для других рам с иной степенью статической определимости. Так что в общем случае можем записать

n

j 1

где n – степень статической неопределимости.

Система уравнений (6.11) называется системой канонических уравнений метода сил.

Здесь требуют однако пояснения вопросы, связанные с наличием внутренних дополнительных связей. Освобождая систему от таких связей, мы заменяем их действие неизвестными внутренними силами, также обозначенными Х. Им соответст-

вуют взаимные смещения элементов рамы i . Например, в

случае трижды статически неопределимой рамы, показанной на рис.6.15, можно выбрать основную систему, показанную на рис.6.15, б, получаемую, если мысленно рассечь стержень АB. В этом случае неизвестными будут нормальная сила Х1, поперечная сила Х2, и изгибающий момент Х3. Понятно, что любой из этих силовых факторов, приложенный к левой части стержня АВ, равен по величине и обратен по направлению приложенному к правой части стержня. Этим силам соответствуют

перемещения: 1 - смещение сечения A относительно сече-

ния B вдоль оси стержня АВ, 2 - смещение сечения A относительно сечения B в направлении, перпендикулярном оси стержня АВ, и 3 - поворот сечения A относительно сечения

B .

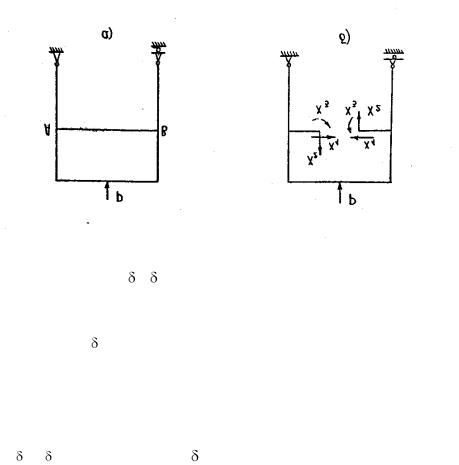
Рис. 6.15

Коэффициенты ij , ip можно определить методом Мора.

Если рама состоит из прямых стержней, то удобно определять их способом Верещагина. В этом случае для определения ко-

эффициента ij ‖перемножаются‖ эпюры изгибающих мо-

ментов от единичной силы, направленной вдоль силы x j и

приложенной в точке еѐ приложения. В силу линейности этих эпюр безразлично, у какой из них определяется площадь, а у какой – момент ―под центром тяжести‖. Поэтому очевидно,

что ij ji . Коэффициенты ip определяются ―умножением‖

так называемой грузовой эпюры, т.е. эпюры изгибающих моментов в основной системе, возникающих вследствие действия на неѐ всех нагрузок, приложенных к раме, на эпюру моментов от единичной силы, направленной вдоль силы Х1 и приложенной в точке еѐ приложения.

Пример. Рассмотрим раму, изображѐнную на рис. 6.16.

Рис. 6.16

На этом же рисунке приведены грузовая эпюра и эпюры от единичных сил, соответствующих силам Х1, Х2. При этом моменты отложены от сжатого волокна. Определим коэффициенты уравнений (6.11), считая жѐсткость на изгиб у стержней ра-

мы одинаковой и равной EI. Величину 11 определяем ―умножением‖ первой единичной эпюры самой на себя. Для этого на каждом участке определяется площадь эпюры изгибающих моментов, которая умножается на величину момента в сечении с координатой центра тяжести этой эпюры: