Сопротивление материалов. Простое деформирование. Воропаев А.А., Томилов Ф.Х

УДК 539.3/7

Воропаев А. А., Томилов Ф. Х. Сопротивление материалов. Простое деформирование: Учеб. пособие. Под ред. А.А. Воропаева. Воронеж: Воронеж. гос. техн. ун-т, 2004. 101 с.

В учебном пособии изложены теоретические основы курса «Сопротивление материалов». Рассматриваются методы расчета на прочность и жесткость при растяжении (сжатии), кручении и изгибе. Теоретический материал сопровождается пояснительными примерами.

Издание предназначено для студентов очной и очнозаочной (вечерней) форм обучения механических специальностей технических вузов.

Учебное пособие подготовлено в электронном виде в текстовом редакторе MS Word XP и содержится в файле сопромат.rar

Ил. 43. Библиогр.: 2 назв.

Научный редактор - канд. техн. наук, доцент В.А. Рябцев

Рецензенты: кафедра естественнонаучных дисциплин Международного института компьютерных технологий (зав. кафедрой проф. С.П. Попов); канд. ф.-м. наук, доцент В.Н.Потапов

©Воропаев А. А., Томилов Ф. Х., 2004

©Оформление. Воронежский государственный технический университет, 2004

ВВЕДЕНИЕ

Сопротивление материалов является одной из базовых образовательных инженерных дисциплин, при изучении которых закладывается фундамент, необходимый для начинающих инженеров в их самостоятельной практической и научной деятельности. Настоящее пособие представляет собой изложение элементарной теории курса «Сопротивление материалов», имеющей широкое приложение в инженерной практике.

Введение в учебные планы технических вузов новых дисциплин привело к существенному сокращению объема часов, выделяемых на изучение курса сопротивления материалов. Восполнение появившихся в результате этого пробелов в знании студентами сопротивления материалов может быть достигнуто в известной мере за счет самостоятельного изучения необходимых разделов дисциплины по курсам лекций, количество которых весьма ограничено. Настоящий курс лекций, написанный в рамках типовой программы для технических вузов, призван частично уменьшить пробел, образовавшийся в этой области за последние годы.

Представленный курс лекций, являющийся пособием для самообразования, преследует цель научить будущего инженера грамотно выбрать необходимый метод расчета и правильно оценить полученный с его помощью результат.

Основой для написания пособия послужили лекции, которые в течение многих лет авторы читали в Воронежском государственном техническом университете, поэтому настоящий курс является в известной мере отражением накопленного ими методического опыта.

Последовательность изложения материала в курсе принята, как правило, от частного к общему. При этом используется принцип постепенного введения новых понятий и терминов, опирающихся на уже известные из смежных дисциплин (теоретическая механика, физика, математика) или ранее введенные. Авторы стремились изложить обширный материал в сжатом виде без ущерба для ясности и строгости изложения.

1. ПРЕДМЕТ И ЗАДАЧИ СОПРОТИВЛЕНИЯ МАТЕРИАЛОВ

1.1.Основные задачи дисциплины

Сопротивление материалов - учебная дисциплина о прочности и жесткости деталей машин и элементов конструкций. Под прочностью понимают способность деталей машин и элементов конструкций сопротивляться эксплуатационным нагрузкам без разрушения. Жесткость – это способность сопротивляться эксплуатационным нагрузкам без недопустимых изменений геометрических размеров. Последнее требует пояснения. Дело в том, что, если в теоретической механике тела рассматриваются как абсолютно твердые, то в сопротивлении материалов тела рассматриваются как деформируемые, т.е. учитывается, что под действием нагрузок происходят изменения формы и размеров тел.

Возьмем, к примеру, колесо турбинной установки. Если колесо недостаточно прочное, то под действием возникающих при его вращении сил инерции оно разрушится, произойдет авария со всеми связанными с ней последствиями. Если же это колесо недостаточно жесткое, то под действием тех же сил инерции диаметр колеса возрастет настолько, что лопатки начнут задевать корпус, что может привести к аналогичным последствиям.

В курсе сопротивления материалов изучаются инженерные, т.е. часто приближенные и достаточно простые, методы расчетов на прочность и жесткость, в результате которых определяются, как говорят, надежные размеры деталей машин и различных конструкций. Определение размеров, при которых детали оказываются достаточно прочными и жесткими, вообще говоря, не проблема. Египетские пирамиды достаточно прочны, хотя и строились задолго до появления нашей науки. Проблема возникает при необходимости удовлетворения противоречивым требованиям. Скажем, необходимость спроектировать достаточно прочную и при этом экономичную конструкцию, или достаточно прочную и вместе с тем легкую ма-

шину. Как правило, повышение прочности достигается увеличением расхода материала. Но увеличение расхода материала снижает экономичность и увеличивает вес конструкции. Для выбора оптимального решения в такого рода ситуациях и нужна соответствующая наука, Когда строили пирамиды, их стоимостью и весом не интересовались. Если бы ракеты строили с таким же запасом прочности, как у пирамид, они бы, как и пирамиды, остались на тысячелетия стоять на Земле.

Во многих случаях качество изделий в первую очередь определяется их прочностью, жесткостью, металлоемкостью. К решению связанных с этим задач и готовит будущих инженеров курс сопротивления материалов.

1.2.РАСЧЕТНАЯ СХЕМА

Реальные детали машин бесконечно сложны. Однако многие из особенностей этих деталей либо не влияют, либо влияют слабо на их прочность и жесткость. Поэтому при выполнении расчетов можно рассматривать не реальный объект, а его расчетную схему, т.е. этот объект, освобожденный от несущественных с точки зрения их влияния на прочность и жесткость особенностей. Переход от реального объекта к расчетной схеме бывает достаточно сложным, поскольку не всегда ясно, что влияет, и что не влияет на прочность. Часто с целью получения практически приемлемых методов расчета приходится пренебречь особенностями рассчитываемых деталей, влияние которых на прочность и жесткость бесспорно.

Переход от реальных объектов к расчетным схемам не является задачей сопротивления материалов, это задача специальных дисциплин. В курсе сопротивления материалов мы, по существу, изучаем некоторый круг расчетных схем. Укажем некоторые из их особенностей. Расчетная схема - это идеализированный определенным образом объект счета. Идеализируются, прежде всего, материал и геометрия тела.

Идеализация материала заключается в том, что чаще всего в дальнейшем он считается сплошным, однородным и изотропным.

Под сплошностью понимается непрерывное заполнение материалом занимаемого им объема. В действительности в любом конструкционном материале имеются пустоты, однако, чаще всего их влияние на прочность несущественно. Гипотеза о сплошности необходима для возможности применения анализа бесконечно малых, т.е. дифференциального и интегрального исчисления.

Под однородностью понимается одинаковость свойств материала в различных точках тела. В действительности свойства реальных тел не однородны на микроуровне, а также часто на макроуровне (свойства поверхностных слоев часто отличны от свойств в глубине материала). Несмотря на это, гипотеза об однородности свойств материала оказывается весьма приемлемой.

Изотропным называют материал, у которого свойства одинаковы в различных направлениях. Примерами анизотропных материалов являются дерево (свойства вдоль волокон отличны от свойств в направлении, поперечном к волокнам), многие пластики, листовой прокат, в особенности из титана и алюминиевых сплавов. Однако многие из конструкционных материалов (например, стали) можно рассматривать как изотропные.

Идеализация геометрии сводится к тому, что рассчитываемые тела чаще всего относят к схемам стержня или оболочки.

Под стержнем понимают тело, у которого одно из измерений (длина) много больше других. На рис. 1.1 схематично показан стержень. Линия АА - его ось. Сечения, перпендикулярные к оси, называются поперечными. Ось стержня - геометрическое место центров тяжести его поперечных сечений. Если ось прямая, стержень называют прямым, если кривая - кривым. Если поперечное сечение не изменяется по длине стержня, его называют стержнем постоянного сечения. В противном случае - стержнем переменного сечения. Примерами стержней являются колонны, балки перекрытий, валы машин.

Если у тела одно из измерений (толщина) пренебрежимо мало по сравнению с другими, то его называют оболочкой. Примерами оболочек являются перекрытия зданий, различные емкости, многочисленные корпусные детали.

В сопротивлении материалов в основном рассматривается прочность и жесткость брусьев.

1.3. Силы внешние и внутренние. Напряжения В технической литературе внешние силы, действующие

на элементы конструкций, называют нагрузками. Рассмотрим классификацию нагрузок.

По характеру изменения во времени нагрузки делят на статические, динамические, циклические.

К статическим относятся нагрузки, изменяющиеся настолько медленно, что возникающие при этом силы инерции не оказывают существенного влияния на прочность и жесткость элементов конструкций.

Если же нагрузки изменяются во времени таким образом, что возникают значительные силы инерции, которые необходимо учитывать в расчетах на прочность и жесткость, нагрузки относят к динамическим.

Нагрузки, периодически изменяющиеся во времени, называют циклическими.

По геометрии области приложения нагрузки делят на сосредоточенные и распределенные.

К сосредоточенным относят нагрузки, область приложения которых достаточно мала. Единицей измерения сосредоточенной нагрузки, если это сила, служит Н, если это момент, то соответственно Нм и их производные.

Нагрузка может быть распределена по длине, по площади или объему. В любом случае количественной мерой такой нагрузки является еѐ интенсивность, под которой понимают соответственно нагрузку, приходящуюся на единицу длины, площади или объема. Если исключить из рассмотрения мо-

ментную нагрузку, то размерностью интенсивности является первом случае Н/м, во втором - Н/м2, в третьем - Н/м3.

Внутренние силы определяются методом сечений, который заключается в следующем. Пусть дано тело, находящееся под действием некоторой системы нагрузок в состоянии равновесия. Тогда можно мысленно рассечь тело в интересующем нас месте, отбросить любую из полученных двух частей вместе с действующими на нее нагрузками, заменить действие отброшенной части внутренними силами, потребовав, чтобы эти силы удовлетворяли всем уравнениям равновесия.

Вернемся к рассмотрению стержня. Возникающую в поперечном сечении стержня систему сил можно, как известно из теоретической механики, привести к центру тяжести. В результате получим главный вектор и главный момент, в общем случае произвольно ориентированные в пространстве. Введем в рассмотрение декартову систему координат x, y, z (рис. 1.2), начало которой совмещено с центром тяжести сечения, ось z направлена по касательной к оси стержня, а оси x, y лежат в плоскости рассматриваемого поперечного сечения. Проецируя главный вектор и главный момент на эти оси, получим три силы: нормальную (или продольную) N и две

поперечные QX, Qy , a также три момента: крутящий Мк и два изгибающих MX , My . Указанные три силы и три момента называются внутренними силовыми факторами в сечении стержня.

Приравняв нулю сумму проекций всех сил, действующих на рассматриваемую часть стержня, получим, что нормальная сила N равна сумме проекций всех внешних сил, приложенных по одну сторону от рассматриваемого сечения, на ось Z .

Приравняв нулю сумму моментов всех сил относительно оси z, получим, что крутящий момент МК равен сумме моментов всех внешних сил, приложенных по одну сторону от сечения, относительно оси z .

Аналогично определяются Qy, Qx, My, Мx.

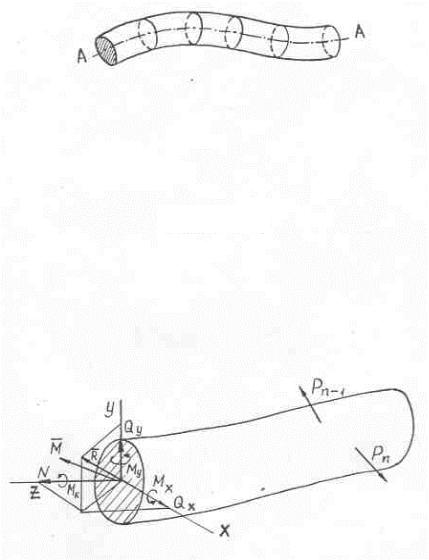
Рис. 1.1

Рис. 1.2

На основе рассмотренной системы внутренних сил вводится классификация видов деформирования .

Если в поперечных сечениях на некотором участке бруса возникают только нормальные силы N, то в зависимости от