1948

II. ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ

1. Основные задачи математической статистики

Разработка методов регистрации, описания и анализа статистических данных, получаемых в результате наблюдения массовых случайных явлений, составляет предмет специаль-

ной науки - математической статистики.

Рассмотрим типичные задачи математической статистики, часто встречаемые на практике.

1.Задача определения закона распределения случайной величины по статистическим данным.

При обработке большого объема статистических данных часто возникает вопрос об определении законов распределения тех или иных случайных величин. Поскольку на практике приходится иметь дело с ограниченным количеством экспериментальных данных, то результаты наблюдений и обработки всегда содержат элемент случайности. Тогда возникает вопрос о том, какие черты наблюдаемого явления относятся к постоянным, действительно присущим ему, а какие являются случайными и проявляются только за счет ограничения экспериментальных данных. Поэтому к методике обработки данных необходимо предъявлять такие требования, чтобы она сохраняла все типичные черты явления и отбрасывала все второстепенные, несущественные, связанные с ограниченным объемом опытного материала. В связи с этим возникает задача сглаживания или выравнивания статистических данных.

2. Задача проверки правдоподобия гипотез.

Эта задача тесно связана с предыдущей. Так как статистический материал всегда ограничен, то выявляющиеся в нем статистические закономерности не лишены случайностей и статистический материал может лишь с большим или с мень-

61

шим правдоподобием подтверждать или не подтверждать справедливость той или иной гипотезы.

3.Задача нахождения неизвестных параметров распределения.

Часто при обработке экспериментальных данных возникает вопрос ни об определении законов распределения случайных величин, (характер закона распределения качественно известен до опыта), а требуется определить некоторые параметры (числовые характеристики) случайной величины. При небольшом числе опытов такая задача не может быть определена точно, как экспериментальный материал, а соответственно и все его параметры содержат элемент случайности. Поэтому может ставиться задача лишь об определении «оценок» или «подходящих значений» для искомых параметров, то есть таких приближенных значений, которые при массовом применении приводили бы в среднем к меньшим ошибкам, чем всякие другие.

2. Статистический ряд. Гистограмма.

Пусть изучается некоторая случайная величина X, закон распределения которой в точности неизвестен, и требуется определить этот закон из опыта или проверить экспериментально гипотезу о том, что величина X подчинена тому или иному закону. С этой целью над величиной X проводится ряд независимых опытов (наблюдений). В каждом из этих опытов случайная величина X принимает определенное значение. Совокупность наблюдаемых значений величины представляет собой первичный статистический материал, подлежащий обработке. Такая совокупность называется «простой статистической совокупностью» или «простым статистическим рядом». Одним из способов обработки простого статистического ряда является построение статистической функции распределения

62

случайной величины.

Статистической функцией распределения случайной ве-

личины X называется частота события X < x в данном статистическом материале

F * x P* X x .

Для того чтобы найти значение статистической функции распределения при данном x, достаточно подсчитать число опытов, в которых величина X приняла значение, меньшее, чем x, и разделить на общее число n проведенных опытов.

Статистическая функция распределения любой случайной величины – прерывной или непрерывной – представляет собой прерывную ступенчатую функцию, скачки которой соответствуют наблюдаемым значения случайной величины и по величине равны частотам этих значений.

При увеличении числа опытов n статистическая функция распределения F * x приближается к подлинной функции распределения F x случайной величины X.

Построение статистической функции распределения уже решает задачу описания экспериментального материала. Однако при большом числе опытов простая статистическая совокупность перестает быть удобной формой записи статистического материала, становится слишком громоздкой и мало наглядной. Статистический материал должен быть подвергнут дополнительной обработке – строится так называемый «статистический ряд». Весь диапазон наблюдаемых значений X делится на интервалы или «разряды» и подсчитывается количество значений mi , приходящееся на каждый i-й разряд. Это

число делится на общее число наблюдений n и находится частота, соответствующая данному разряду:

Pi* mni .

63

Сумма частот всех разрядов равна единице.

Таблица, в которой приведены разряды в порядке их расположения вдоль оси абсцисс и соответствующие частоты на-

зывается статистическим рядом:

Значение, находящееся в точности на границе двух разрядов считают в равной степени принадлежащем к обоим разрядам и прибавляют к числам mi того и другого разряда по ½.

Число разрядов, на которые следует группировать статистический материал не должно быть слишком большим, (ряд становится невыразительным) и слишком маленьким (свойства распределения описываются слишком грубо). Рационально выбирать число разрядов 10 - 20. Длины разрядов могут быть как одинаковыми, так и разными.

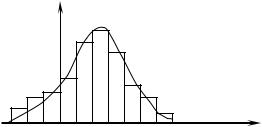
Статистический ряд часто оформляется в виде так называемой гистограммы. Гистограмма строится следующим образом. По оси абсцисс откладываются разряды, и на каждом из разрядов как на основании строится прямоугольник, площадь которого равна частоте данного разряда. В качестве высоты прямоугольника берется частота разряда, деленная на его длину. В случае равных по длине разрядов высоты прямоугольников пропорциональны соответствующим частотам. Полная площадь гистограммы равна единице.

При увеличении числа опытов можно выбирать все более и более мелкие разряды; при этом гистограмма будет все более приближаться к некоторой кривой, ограничивающей площадь, равную единице. Эта кривая представляет собой график плотности распределения величины Х.

64

3. Числовые характеристики статистического распределения

Ранее мы рассмотрели числовые характеристики случайных величин: математическое ожидание и дисперсию. Аналогичные числовые характеристики существуют и для статистических распределений. Каждой случайной величине Х соответствует ее статистическая аналогия. Для математического ожидания случайной величины такой аналогией является среднее арифметическое наблюдаемых значений случайной величины:

n

xi

где xi – значение случайной величины, наблюдаемое в i–м опыте, n - число опытов. В дальнейшем эту характеристику будем называть статистическим средним случайной величины.

При неограниченном числе опытов статистическое среднее приближается к математическому ожиданию. При ограниченном числе опытов статистическое среднее является случайной величиной, которая, тем не менее, связана с математическим ожиданием и может дать о нем представление. В дальнейшем статистические аналогии будем снабжать значком *.

Статистическая дисперсия случайной величины Х:

В ряде руководств по математической статистике статистическое среднее именуется «выборочным средним», а стати-

65

стическая дисперсия – «выборочной дисперсией».

Происхождение этих терминов следующее. В статистике часто приходится исследовать распределение того или иного признака для весьма большой совокупности индивидуумов, образующих статистический коллектив (длина или вес тела какого-либо из группы животных; стандартность или размер детали из их большого числа). Данный признак является случайной величиной, значение которого от индивидуума к индивидууму или от детали к детали меняется. Однако чтобы составить представление о распределении этой случайной величины или о ее важнейших характеристиках, нет необходимости исследовать каждый индивидуум, можно исследовать некоторую выборку достаточно большого объема для того, чтобы в ней были выявлены существенные черты изучаемого распределения. Та обширная совокупность, из которой производится выборка, называется генеральной совокупностью. При этом предполагается, что число членов N в генеральной совокупности весьма велико, а число членов n в выборке ограничено.

При составлении выборки можно поступать двумя способами: после того, как объект отобран и над ним произведено наблюдение, он может быть возвращен либо не возвращен в генеральную совокупность. В связи с этим выборки подразде-

ляют на повторные и бесповторные.

Повторной называют выборку, при которой отобранный объект (перед отбором следующего) возвращается в генеральную совокупность.

Бесповторной называют выборку, при которой отобранный объект в генеральную совокупность не возвращается.

На практике обычно пользуются бесповторным случайным отбором.

Для того чтобы выборка правильно отражала все черты генеральной совокупности, она должна быть репрезентативной (представительной). Выборка будет репрезентативной,

66

если каждый ее объект отобран случайно из генеральной совокупности, а все объекты имеют одинаковую вероятность попасть в выборку.

Существуют следующие способы отбора.

1.Отбор, не требующий расчленения генеральной совокупности на части. Сюда относятся: простой случайный беспо-

вторный отбор; простой случайный повторный отбор. Про-

стым случайным называют такой отбор, при котором объекты извлекают по одному из всей генеральной совокупности.

2.Отбор, при котором генеральная совокупность разби-

вается на части: типический отбор; механический отбор; се-

рийный отбор. Типическим называют отбор, при котором объекты отбираются не из всей генеральной совокупности, а из каждой ее «типической» части. Типическим отбором пользуются тогда, когда обследуемый признак заметно колеблется в различных типических частях генеральной совокупности. Механическим называют отбор, при котором генеральную совокупность «механически» делят на несколько групп, столько, сколько объектов должно войти в выборку, а из каждой группы отбирают один объект. Серийным называют отбор, при котором объекты отбирают из генеральной совокупности не по одному, а «сериями», которые подвергают сплошному обследованию.

На практике часто применяют комбинированный отбор, при котором сочетаются указанные способы.

При достаточно большом числе членов генеральной совокупности N оказывается, что свойства выборочных (статистических) распределений и характеристик практически не зависят от N, отсюда вытекает математическая идеализация, состоящая в том, что генеральная совокупность, из которой осуществляется выбор, имеет бесконечный объем. При этом отличают точные характеристики (закон распределения, математическое ожидание, дисперсию и т.д.), относящиеся к генеральной совокупности, от аналогичных им «выборочных» характе-

67

ристик. Выборочные характеристики отличаются от соответствующих характеристик генеральной совокупности за счет ограниченности объема выборки n. При неограниченном увеличении n все выборочные характеристики приближаются к соответствующим характеристикам генеральной совокупности.

4. Выравнивание статистических рядов

При обработке статистического материала часто приходится решать вопрос о том, как подобрать для статистического ряда плавную теоретическую кривую распределения, выражающую лишь существенные черты статистического материала, а не случайности, связанные с недостаточным объемом экспериментальных данных (рис. 4). Такая задача называется задачей выравнивания (сглаживания) статистических рядов.

f(х)

х

0

Рис. 4

Как правило, принципиальный вид теоретической кривой выбирается заранее, в соответствии с задачей, а в некоторых случаях с внешним видом статистического распределения. Аналитическое выражение выбранной кривой распределения зависит от некоторых параметров; задача выравнивания статистического ряда переходит в задачу рационального выбора

68

тех значений параметров, при которых соответствие между статистическим и теоретическим распределениями оказывается наилучшим. При сглаживании эмпирических зависимостей или при подборе параметров распределения применяют метод наименьших квадратов.

5. Критерии согласия

Рассмотрим вопрос, связанный с согласованием теоретического и статистического распределений, а именно вопрос проверки гипотез.

Пусть статистическое распределение выровнено с помощью некоторой теоретической кривой f(x) (рис. 4). Между теоретическим и статистическим распределениями неизбежны некоторые расхождения, как бы хорошо ни была подобрана кривая. Возникает вопрос: объясняются ли эти расхождения только лишь случайными обстоятельствами, связанными с ограниченным числом наблюдений, или они существенны и связаны с тем, что данная кривая плохо выравнивает данное статистическое распределение. Для ответа на этот вопрос служат так называемые «критерии согласия».

Рассмотрим один из наиболее часто применяемых критериев согласия – так называемый «критерий 2 » Пирсона.

Пусть произведено n независимых опытов, в каждом из которых величина Х приняла определенное значение. Результаты опытов сведены в k разрядов в виде статистического ряда:

69

ные с гипотезой о том, что случайная величина Х имеет данный закон распределения (заданный функцией распределения F(x) или плотностью f(x)), который назовем «теоретическим».

Зная теоретический закон распределения, можно найти теоретические вероятности попадания случайной величины в каждый из разрядов: p1, p2, . . ., pk.

Проверяя согласованность теоретического и статистического распределений, исходят из расхождений U между теоретическими вероятностями pi и наблюдаемыми частотами pi*(за счет чисто случайных причин). В качестве меры расхождения между теоретическим и статистическим распределениями выбирается сумма квадратов отклонений (pi*- pi), взятая с некоторыми «весами» сi:

Коэффициенты сi вводят потому, что в общем случае отклонения, относящиеся к различным разрядам, нельзя считать равноправными по значимости. Одно и то же по абсолютной величине отклонение (pi*- pi) может быть мало значительным, если сама вероятность pi велика, и очень заметным, если она мала. Поэтому в качестве сi Пирсон предложил отношение

тогда мера расхождения обозначается 2 :

Для удобства вычислений применяется формула

70