1948

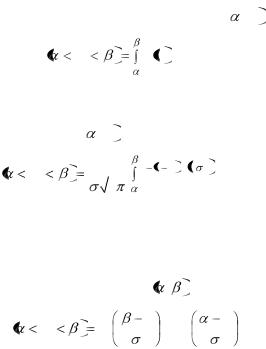
нормальной кривой (кривой Гаусса) (рис. 2, 3).

С возрастанием максимальная ордината нормальной кривой убывает, а сама кривая становится более пологой, т.е. сжимается к оси Ох; при убывании нормальная кривая становится более «островершинной» и растягивается в положительном направлении оси Оу (рис. 3).

2.10. Вероятность попадания в заданный интервал нормальной случайной величины

Как было сказано ранее, если случайная величина Х задана плотностью распределения f(x), то вероятность того, что Х примет значение, принадлежащее интервалу , , 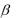такова:

Пусть случайная величина Х распределена по нормальному закону. Тогда вероятность того, что Х примет значение, принадлежащее интервалу , , равна

Преобразовав эту формулу так, чтобы можно было пользоваться готовыми таблицами, окончательно получаем формулу для вычисления вероятности того, что непрерывная случайная величина, распределенная по нормальному закону, примет

51

Пример 9. Случайная величина Х распределена по нормальному закону. Математическое ожидание и среднее квадратическое отклонение этой величины соответственно равны 30 и 10. Найти вероятность того, что Х примет значение, принадлежащее интервалу (10, 50).

Решение: Воспользуемся формулой (8). По условию,

По таблице находим Ф(2)=0,4772. Отсюда, искомая вероятность

P 10 X 50 2 0,4772 0,9544.

Если распределение изучаемой случайной величины неизвестно, то можно использовать правило трех сигм: если случайная величина распределена нормально, то абсолютная величина ее отклонения от математического ожидания не превосходит утроенного среднего квадратического отклонения. Если это условие выполняется, то есть основание предполагать, что изучаемая величина распределена нормально; в противном случае она не распределена нормально.

52

Вопросы для самопроверки

1.Дайте классическое определение вероятности. В чем состоит различие между вероятностью и относительной частотой?

2.Дайте определение условной вероятности. Какие события называют независимыми?

3.Дайте определение произведения событий.

4.Запишите формулу полной вероятности, формулу Бейеса, формулу Бернулли. Сформулируйте локальную теорему Лапласа, интегральную теорему Лапласа, теорему Пуассона. Когда применяются эти теоремы?

5.Дайте определение случайной величины. Приведите примеры.

6.Дайте определение функции распределения случайной величины. Каковы ее свойства?

7.Дайте определение плотности распределения вероятностей. Каковы ее свойства?

8.Как найти вероятность попадания случайной величины в заданный интервал, если она распределена по нормальному закону?

9.Дайте определение математического ожидания случайной величины. Каковы его свойства?

10.Дайте определение дисперсии случайной величины. Каковы ее свойства?

11.Дайте определение среднего квадратического отклонения случайной величины и укажите его преимущества по сравнению с дисперсией.

53

Задачи для самостоятельного решения

1. В ящике имеется 50 одинаковых деталей, из них 5 окрашенных. Наудачу вынимают одну деталь. Найти вероятность того, что извлеченная деталь окажется окрашенной.

Ответ. р = 0,1.

2. Брошена игральная кость. Найти вероятность того, что выпадет четное число очков.

Ответ. р = 0,5.

3. Участники жеребьевки тянут из ящика жетоны с номерами от 1 до 100. Найти вероятность того, что номер первого наудачу извлеченного жетона не содержит цифры 5.

Ответ. р = 0,81.

4. В мешочке имеется 5 одинаковых кубиков. На всех гранях каждого кубика написана одна из следующих букв: о, п, р, с, т. Найти вероятность того, что на вынутых по одному и расположенных «в одну линию» кубиков можно будет прочесть слово «спорт».

Ответ. р = 1/120.

5. В партии из 100 деталей отдел технического контроля обнаружил 5 нестандартных деталей. Чему равна относительная частота появления нестандартных деталей?

Ответ. р = 0,05.

54

6. В денежно-вещевой лотерее на каждые 10000 билетов разыгрывается 150 вещевых и 50 денежных выигрышей. Чему равна вероятность выигрыша, безразлично денежного или вещевого, для владельца одного лотерейного билета?

Ответ. р = 0,02.

7. Вероятность того, что стрелок при одном выстреле выбьет 10 очков, равна 0,1; вероятность выбить 9 очков равна 0,3; вероятность выбить 8 или меньше очков равна 0,6. Найти вероятность того, что при одном выстреле стрелок выбьет не менее 9 очков.

Ответ. р = 0,4.

8. В партии из 10 деталей 8 стандартных. Найти вероятность того, что среди наудачу извлеченных 2 деталей есть хотя бы одна стандартная.

Ответ. р = 44/45.

9. В ящике 10 деталей, среди которых 2 нестандартных. Найти вероятность того, что в наудачу отобранных 6 деталях окажется не более одной нестандартной детали.

Ответ. р = 2/3.

10. Вероятность того, что стрелок при одном выстреле попадает в мишень, равна р = 0,9. Стрелок произвел 3 выстрела. Найти вероятность того, что все 3 выстрела дали попадание.

Ответ. 0,729.

55

11. Брошены монета и игральная кость. Найти вероятность совмещения событий: «появился «орел»», «появилось 6 очков».

Ответ. 1/12.

12. В двух ящиках находятся детали: в первом—10 (из них 3 стандартных), во втором—15 (из них 6 стандартных). Из каждого ящика наудачу вынимают по одной детали. Найти вероятность того, что обе детали окажутся стандартными.

Ответ. 0,12.

13. В студии телевидения 3 телевизионных камеры. Для каждой камеры вероятность того, что она включена в данный момент, равна р = 0,6. Найти вероятность того, что в данный момент включена хотя бы одна камера (событие А).

Ответ. 0,936.

14. Чему равна вероятность того, что при бросании трех игральных костей 6 очков появится хотя бы на одной из костей (событие А)?

Ответ. 91/216.

15. Предприятие изготовляет 95% изделий стандартных, причем из них 86% — первого сорта. Найти вероятность того, что взятое наудачу изделие, изготовленное на этом предприятии, окажется первого сорта.

Ответ. 0,817.

56

16. Вероятность того, что событие А появится хотя бы один раз при двух независимых испытаниях, равна 0,75. Найти вероятность появления события в одном испытании (предполагается, что вероятность появления события в обоих испытаниях одна и та же).

Ответ. 0,5.

17. Вероятность поражения цели первым стрелком при одном выстреле равна 0,8, а вторым стрелком — 0,6. Найти вероятность ого, что цель будет поражена только одним стрелком.

Ответ. 0,44.

18. Два стрелка произвели по одному выстрелу. Вероятность попадания в мишень первым стрелком равна 0,7, а вторым - 0,6. Найти вероятность того, что хотя бы один из стрелков попал в мишень.

Ответ. 0,88.

19. У сборщика имеется 16 деталей, изготовленных заводом № 1, 4 детали завода № 2. Наудачу взяты 2 детали. Найти вероятность того, что хотя бы одна из них окажется изготовленной заводом № 1.

Ответ. 92/95.

20. В группе спортсменов 20 лыжников, 6 велосипедистов и 4 бегуна. Вероятность выполнить квалификационную норму такова: для лыжника — 0,9, для велосипедиста — 0,8 и для бегуна — 0,75. Найти вероятность того, что спортсмен, выбранный наудачу, выполнит норму.

Ответ. 0,86.

57

21. Сборщик получил 3 коробки деталей, изготовленных заводом № 1, и 2 коробки деталей, изготовленных заводом №2. Вероятность того, что деталь завода № 1 стандартна, равна 0,8, а завода № 2 — 0,9. Сборщик наудачу извлек деталь из наудачу взятой коробки. Найти вероятность того, что извлечена стандартная деталь.

Ответ. 0,84.

22. В первом ящике содержится 20 деталей, из них 15 стандартных; во втором — 30 деталей, из них 24 стандартных; в третьем 10 деталей, из них 6 стандартных. Найти вероятность того, что наудачу извлеченная деталь из наудачу взятого ящика - стандартная.

Ответ. 43/60.

23. В ящик, содержащий 3 одинаковых детали, брошена стандартная деталь, а затем наудачу извлечена одна деталь. Найти вероятность того, что извлечена стандартная деталь, если равновероятны все возможные предположения о числе стандартных деталей, первоначально находящихся в ящике.

Ответ. 0,625.

24. Для участия в студенческих отборочных спортивных соревнованиях выделено из первой группы курса 4, из второй - 6, из третьей группы - 5 студентов. Вероятности того, что студент первой, второй и третьей группы попадает в сборную института, соответственно равны 0,9; 0,7 и 0,8. Наудачу выбранный студент в итоге соревнования попал в сборную. К какой из групп вероятнее всего принадлежал этот студент?

Ответ. Вероятности того, что выбран студент первой, второй, третьей групп, соответственно равны: 18/59, 21/59,

20/59.

58

25.В цехе 6 моторов. Для каждого мотора вероятность того, что он в данный момент включен, равна 0,8. Найти вероятность того, что в данный момент: а) включено 4 мотора; б) включены все моторы;

в) выключены все моторы.

Ответ. а) Р6(4) = 0,246; б) Р6(6) = 0.26; в) Р6(0) = 0,000064.

26. Найти вероятность того, что событие А появится в пяти независимых испытаниях не менее двух раз, если в каждом испытании вероятность появления события А равна

0,3.

Ответ. Р= 0,472.

27. Произведено 8 независимых испытаний, в каждом из которых вероятность появления события А равна 0,1. Найти вероятность того, что событие А появится хотя бы 2 раза.

Ответ. Р=1 - [Р8(0) + Р8 (1)] = 0,19.

28. Монету бросают 6 раз. Найти вероятность того, что герб выпадет: а) менее двух раз; б) не менее двух раз.

Ответ. а) Р=7/64; б) Р=57/64.

29. Найти приближенно вероятность того, что при 400 испытания событие наступит ровно 104 раза, если вероятность его появления в каждом испытании равна 0,2.

Ответ. Р400(104) =0,0006.

30. Вероятность поражения мишени стрелком при одном

59

выстреле равна 0,75. Найти вероятность того, что при 100 выстрелах мишень будет поражена: а) не менее 70 и не более 80 раз; б) не более 70 раз.

Ответ. а) Р100(70,80) = 2Ф(1,15) = 0,7498;

б) Р100(0; 70)=-Ф(1,15) + 0,5 = 0,1251.

31. Найти математическое ожидание дискретной случайной величины, зная закон ее распределения:

Ответ. 2,6.

32. Производится 4 выстрела с вероятностью попадания в цель р1 = 0,6, р2 = 0,4, р3 = 0,5 и р4 = 0,7. Найти математическое ожидание общего числа попаданий.

Ответ. 2,2 попадания.

33. Вероятность отказа детали за время испытания на надежность равна 0,2. Найти математическое ожидание числа отказавших деталей, если испытанию будут подвергнуты 10 деталей.

Ответ. 2 детали.

34. Найти математическое ожидание произведения числа очков, которые могут выпасть при одном бросании двух игральных костей.

Ответ.12,25 очка.

35. Найти математическое ожидание числа лотерейных билетов, на которые выпадут выигрыши, если приобретено 20 билетов, причем вероятность выигрыша по одному билету равна 0,3.

Ответ.6 билетов.

60