1948

Две случайные величины называют независимыми, если закон распределения одной из них не зависит от того, какие возможные значения приняла другая величина.

Свойство 3. Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий:

М (XY) = М ( Х ) М (Y).

Свойство 4. Математическое ожидание суммы двух случайных величин равно сумме математических ожиданий слагаемых:

М (X+Y) = М ( Х ) + М (Y).

Найдем математическое ожидание числа появлений события в независимых испытаниях. Пусть производится п независимых испытаний, в каждом из которых вероятность появления события А постоянна и равна р. Тогда математическое ожидание М(Х) числа появлений события А в п независимых испытаниях (биномиального распределения с параметрами п и р ) равно произведению числа испытаний на вероятность появления события в каждом испытании:

М ( Х ) = п р

Пример 4. Вероятность попадания в цель при стрельбе из орудия р=0,6. Найти математическое ожидание общего числа попаданий, если будет произведено 10 выстрелов.

Решение. Попадание при каждом выстреле не зависит от исходов других выстрелов, поэтому рассматриваемые события независимы и, следовательно, искомое математическое ожидание

М ( Х ) = пр = 100,6 = 6.

41

2.5. Дисперсия дискретной случайной величины

На практике часто требуется оценить рассеяние возможных значений случайной величины вокруг ее среднего значения. Например, в артиллерии важно знать, насколько кучно лягут снаряды вблизи цели, которая должна быть поражена. Зная лишь математическое ожидание случайной величины, еще нельзя судить ни о том, какие возможные значения она может принимать, ни о том, как они рассеяны вокруг математического ожидания. Другими словами, математическое ожидание полностью случайную величину не характеризует.

По этой причине наряду с математическим ожиданием вводят и другие числовые характеристики. Так, например, для того чтобы оценить, как рассеяны возможные значения случайной величины вокруг ее математического ожидания, пользуются, в частности, числовой характеристикой, которую называют дисперсией.

Введем понятие отклонения случайной величины от ее математического ожидания. Пусть X — случайная величина и М(Х)—ее математическое ожидание. Рассмотрим в качестве новой случайной величины разность X - М(Х).

Отклонением называют разность между случайной величиной и ее математическим ожиданиям. Практическая значимость отклонения невелика, поскольку математическое ожидание отклонения равно нулю:

М [X - М(Х)]=0.

Дисперсией (рассеянием) дискретной случайной величины

называют математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:

D(X)=M[Х-M(X)]2.

Для вычисления дисперсии часто бывает удобно пользоваться следующей теоремой.

42

Теорема. Дисперсия случайной величины Х равна разности между математическим ожиданием квадрата случайной величины Х и квадратом ее математического ожидания:

D(X)=M(X2)-[M(X)]2. (7)

Пример 5. Найти дисперсию случайной величины X, которая задана следующим законом распределения:

р0,1 0,6 0,3

Решение. Найдем математическое ожидание М (X):

М (X) = 2 0,1 30,6 50,3 3,5 .

Найдем математические ожидания М (X2):

М (X2) = 4 0,1 9 0,6 250,3 13,3.

Искомая дисперсия

D(X)=M(X2)-[M(X)]2=13,3-(3,5)2=1,05.

Рассмотрим свойства дисперсии.

Свойство 1. Дисперсия постоянной величины С равна нулю:

D(C)=0.

Это свойство объясняется тем, что постоянная величина сохраняет одно и то же значение.

Свойство 2. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат:

D(СX)=С2 D(X).

Свойство 3. Дисперсия суммы двух независимых случайных величин равна сумме дисперсией этих величин:

D(X+Y)= D(X)+D(Y).

43

Следствие 1. Дисперсия суммы нескольких взаимно независимых случайных величин равна сумме дисперсией этих величин.

Следствие 2. Дисперсия суммы постоянной величины и случайной равна дисперсии случайной величины:

Свойство 4. Дисперсия разности двух независимых случайных величин равна сумме их дисперсией:

D(X-Y)= D(X)+D(Y).

2.6. Среднее квадратическое отклонение

Для оценки рассеяния возможных значений случайной величины вокруг ее среднего значения кроме дисперсии служит еще и другая характеристика, называемая средним квадратическим отклонением.

Средним квадратическим отклонением случайной вели-

чины Х называют квадратный корень из дисперсии:

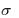X D X .

Размерность X совпадает с размерностью Х, поэтому

в тех случаях, когда желательно, чтобы оценка рассеяния имела размерность случайной величины, вычисляют средне квадратическое отклонение, а не дисперсию.

2.7. Функция распределения вероятностей непрерывной случайной величины

Функцией распределения непрерывной случайной величи-

ны называют функцию F(x), определяющую вероятность того, что случайная величина Х в результате испытания примет значение, меньшее х, т.е.

44

F(x)=Р(Х<x).

Геометрически это равенство можно истолковать так: F(x) есть вероятность того, что случайная величина примет значение, которое изображается на числовой оси точкой, лежащей левее точки х.

Рассмотрим свойства функции распределения.

Свойство 1. Значения функции распределения принадлежат отрезку [0,1]:

0 F x 1.

Свойство 2. F(x) – неубывающая функция, т.е.

F x2 F x1 , если x2 x1 .

Следствие 1. Вероятность того, что случайная величина примет значение, заключенное в интервале (a,b), равна приращению функции распределения на этом интервале:

P(a X b) F b F a .

Следствие 2. Вероятность того, что непрерывная случайная величина Х примет одно определенное значение, равна нулю.

Свойство 3. Если возможные значения случайной величины принадлежат интервалу (a,b),то 1) F(x)=0 при x a ;

2) F(x)=1 при x b .

Следствие. Если возможные значения непрерывной слу-

непрерывной случайной величины расположен в полосе, огра-

45

ниченной прямыми у=0, у=1 и изображен на рис.1. График функции распределения дискретной случайной величины имеет ступенчатый вид.

Непрерывную случайную величину можно задать, используя кроме функции распределения F(x), функцию, назы-

ваемую плотностью распределения или плотностью вероятности.

Плотностью распределения вероятностей непрерывной случайной величины Х называют функцию f(x) – первую производную от функции распределения F(x):

f(x)= F x .

Зная плотность распределения, можно вычислить вероятность того, что непрерывная случайная величина примет значение, принадлежащее заданному интервалу.

Теорема. Вероятность того, что непрерывная случайная величина Х примет значение, принадлежащее интервалу (a,b), равна определенному интегралу от плотности распределения, взятому в пределах от а до b :

Геометрически полученный результат можно истолковать так: вероятность того, что непрерывная случайная величина примет значение, принадлежащее интервалу (a,b), равна площади криволинейной трапеции, ограниченной осью Ох, кривой распределения f(x) и прямыми x=a и x=b.

Пример 6. Задана плотность распределения вероятности случайной величины Х

46

Найти вероятность того, что в результате испытания Х примет значение, принадлежащее интервалу (0,5; 1).

Решение: Искомая вероятность

1

P 0,5 X 1 2 xdx x2 10,5 1 0,25 0,75.

0,5

Зная плотность распределения f(x), можно найти функцию распределения F(x) по формуле

x

F(x)= f x dx ,

а, зная функцию распределения, может быть найдена плотность распределения, а именно:

f(x)= Fx .

Пример 7. Найти функцию распределения по данной плотноcти распределения:

47

Итак, искомая функция распределения равна

Рассмотрим свойства плотности распределения.

Свойство 1. Плотность распределения – неотрицательная функция:

f(x) 0 .

Свойство 2. Несобственный интеграл от плотности распределения в пределах от до равен единице:

f x dx =1.

Геометрически это означает, что вся площадь криволинейной трапеции, ограниченной осью Ох и кривой распределения, равна единице.

В частности, если все возможные значения случайной величины принадлежат интервалу (a,b), то

b

f x dx =1.

a

2.8. Числовые характеристики непрерывных случайных величин

Математическим ожиданием непрерывной случайной величины Х, возможные значения которой принадлежат отрезку [a,b], называют определенный интеграл

b

М(х)= xf x dx .

a

48

Дисперсией непрерывной случайной величины называют математическое ожидание квадрата ее отклонения. Если возможные значения Х принадлежат отрезку [a,b], то

b

D x [x M X ]2 f x dx .

a

Среднее квадратическое отклонение непрерывной слу-

чайной величины определяется, как и для величины дискретной

а, функцию распределения случайной величины, математическое ожидание М [X], дисперсию D [X], вероятность выполнения неравенства 0 < х < 3.

т.к. при x [2,4] плотность распределения равна нулю, то

2

Функция распределения связана с функцией плотности соотношением

Математическое ожидание М [Х] и дисперсию D [Х] определим по формулам

49

2

Вероятность выполнения неравенства 0 < х < 3 определим по формуле

3

Р( 0 < х < 3)= f x dx F(3) - F(0) =1/2 - 0 =1/2.

0

2.9. Нормальное распределение

Нормальным называют распределение вероятностей непрерывной случайной величины, которое описывается плотностью

Здесь a - математическое ожидание, - среднее квадратическое отклонение нормального распределения. Достаточно знать эти два параметра, чтобы задать нормальное распределе-

ние. График плотности нормального распределения называют

50