
1005
.pdfОбратное преобразование Фурье (F–1-преобразование) позволяет получить функцию h(t) из H(f):
h(t) = F −1 {H ( f )} |
|
∞ |
|
|
|
= ∫ H ( f )e j 2πft df |
(2.5) |
||||
или |
|
−∞ |
|
||
|
|
|
|
|
|
h(t) = F −1 {H (ω)} = |
|
1 |
|
∞ |
|
|
∫ H (ω)e jωt dω. |
(2.6) |
|||
|
2π |
||||
|
|
−∞ |
|
||
|
|
|
|
|
|
При построении цифрового фильтра в противоположность аналоговому случаю нет необходимости вводить условие физической осуществимости. Иначе говоря, не нужно требовать, чтобы весовая функция была равна нулю при τ < 0, поскольку данные могут быть накоплены в ЭВМ и в нужный момент поданы на фильтр для фильтрации их в обратном порядке.
Идеальным фильтром можно считать систему, имеющую одну полосу пропускания или более (ряд частот, для которых |H(f)| = 1) и одну полосу непрозрачности или более (ряд частот, для которых |H(f)| = 0). Простые идеальные фильтры обычно подразделяют на фильтры нижних и верхних частот и полосовые. Примеры идеальных амплитудно-частотных характеристик (АЧХ) |H(f)| низкочастотного, высокочастотного и полосового фильтров даны на рис. 2.4–2.6 соответственно, где f0 – частота среза или граничная частота первых двух фильтров; f1, f2 – частоты среза (граничные частоты) полосового фильтра. Примерный вид реальных амплитудно-частотных характеристик |H(f)| низкочастотного, высокочастотного и полосового фильтров показан на рис. 2.7–2.9 соответственно.
Применяя преобразование Фурье к левой и правой частям формулы (2.1), получим
Y ( f ) = H ( f )x( f ), |
(2.7) |
где X(f) – преобразование Фурье процесса на входе фильтра x(t), т.е. X ( f ) = F {x(t)} ; Y(f) – преобразование Фурье процесса
41

на выходе фильтра y(t). Соотношение (2.7) можно записать также в виде
|
|
Y (ω) = H (ω) X (ω). |
(2.8) |
|
|H(f)| |
|H(f)| |
|
1 |
|
1 |
|
|
|
||
|
|
|
|
0 |
f0 |
f |
0 |
f0 |
f |
Рис. 2.4. Пример идеальной АЧХ |
Рис. 2.5. Пример идеальной АЧХ |
||||
низкочастотного фильтра |
высокочастотного фильтра |
||||
|H(f)|
|H(f)|
1
1
0 f1 f2 f 0 f
Рис. 2.6. Пример идеальной АЧХ |
Рис. 2.7. Вид реальной АЧХ |
полосового фильтра |
низкочастотного фильтра |
|H(f)| |
|H(f)| |
|
|
1 |
1 |
|
0 |
f 0 |
f |
Рис. 2.8. Вид реальной АЧХ |
|
Рис. 2.9. Вид реальной АЧХ |
высокочастотного фильтра |
|
полосового фильтра |
42
Уравнение (2.7) является эквивалентом уравнения (2.1) в частотной области.
Таким образом, использовав частотную характеристику фильтра и выполнив преобразование Фурье процессов на его входе и выходе, можно свести интеграл свертки (2.1) к простым алгебраическим выражениям (2.7) или (2.8).
Частотная характеристика фильтра в общем случае является комплексной величиной, которую удобно представить через ее модуль и аргумент. Для этого следует переписать H(f)
в показательной форме: |
|
H ( f ) =| H ( f ) | e jΨ( f ). |
(2.9) |
Модуль |H(f)| называется амплитудно-частотной характеристикой (АЧХ) фильтра, а аргумент Ψ(f) – фазочастотной характеристикой (ФЧХ) фильтра. Для частотной характеристики, АЧХ и ФЧХ, справедливы следующие свойства:
H (− f ) = H * ( f ), | H (− f ) | =| H ( f ) |, Ψ(− f ) = −Ψ( f ), (2.10)
где H*(f) – функция частоты, комплексно-сопряженная с функцией частоты H(f).
Если применить обратное преобразование Фурье (2.5) к правой части уравнения (2.7), то получим выходной сигнал фильтра:
∞∞
y(t) = ∫ H ( f )X ( f )e j 2πft df = ∫ X ( f ) | H ( f ) | e j[2πft+Ψ( f )]df . (2.11)
−∞ −∞
Сравнивая уравнения (2.11) и (2.1), видим, что линейный фильтр одинаково хорошо описывается весовой функцией или частотной характеристикой соответственно во временной или в частотной области. Во временной области результат фильтрации может быть вычислен непосредственно через интеграл свертки, а в частотной – через прямое и обратное преобразование Фурье. На рис. 2.10 показаны принципы фильтрации во временной и частотной областях.
43

|
Свертка |
||
x(t) |
|
Временное |
|
|
|||
h(t) |
представление |
||
|
|
||
|
|
y(t) |
|
|
|
|
|
F |
F |
||
|
|
F–1 |
|
|
|
Y(ω) |
|
|
H(ω) |
||
X(ω) |
Частотное |
||
|
|||
|
|
представление |
|
|
|
||
|
Умножение |
||
Входной |
|
Выходной |
|
сигнал |
|
сигнал |
|
Рис. 2.10. Фильтрация во временной и частотной областях
Нерекурсивные цифровые фильтры
Цифровые фильтры можно разделить на нерекурсивные и рекурсивные.
Прямоугольная аппроксимация интеграла свертки (2.1) имеет вид
|
|
M |
|
|
|
|
|
|
|
|
|
|
yn = ∆t ∑ hk*xn+k , |
h = M +1, |
M + 2, ..., |
(2.12) |
|||||||||
|
|
k =−M |
|
|
|
|
|
|
|
|
|
|
где |
|
|
|
|
|
|
|
|
|
|
|
|
h* = h(t |
k |
); t |
k |
= k∆t; y |
n |
= y(t |
n |
); t |
n |
= n∆t; |
|
|
k |
|
|
|
|
|
|
|
|||||
xn+k = x(tn+k ); tn+k = (n + k)∆t;
44
M – константа или параметр фильтра; ∆t – интеграл дискретности измерений датчиком сигнала x(t).
Введем обозначение hk = hk*∆t. Тогда соотношение (2.12) примет вид
M |
|
yn = ∑ nk xn+k , |
(2.13) |
k =−M
где hk – весовые коэффициенты фильтра. Соотношение (2.13) определяет алгоритм цифровой фильтрации с использованием нерекурсивного цифрового фильтра.
Для симметричного нерекурсивного цифрового фильтра имеет место соотношение
hk = h−k , k =1, 2, ..., M .
В случае симметричного фильтра эквивалентная уравнению (2.2) конечная сумма определяет фильтр, ФЧХ которого равна нулю, и АЧХ
M |
|
| H ( f ) |= H ( f ) = h0 +2∑hi cos(2πfi∆t). |
(2.14) |
i=1
Если известна АЧХ симметричного фильтра, то весовые коэффициенты определяются обратным преобразованием Фурье уравнения (2.14) в виде
∞ |
|
hi = ∫ H ( f )cos(2πfi∆t)df , i = 0,1, ..., M . |
(2.15) |
−∞
В случае, когда hk = 0 при k < 0, из уравнения (2.12) имеем
M |
|
yn = ∑hk xn−k . |
(2.16) |
k=0
45
Рекурсивные цифровые фильтры
Рекурсивный фильтр описывается уравнением
M |
N |
|
yn = ∑ hk xn−k +∑dk yn−k . |
(2.17) |
|
k =−M |
k=1 |
|
Коэффициенты hk и dk являются константами. В том случае, когда все коэффициенты dk равны нулю, фильтр называется нерекурсивным.
В случае, когда hk = 0 при k < 0, уравнение (2.17) примет
вид
M |
N |
|
yn = ∑hk xn−k +∑dk yn−k . |
(2.18) |
|
k=0 |
k=1 |
|
Преобразование Фурье для уравнения (2.17) дает
M |
|
Y ( f ) = X ( f ) ∑ hk e− j 2 |
πfk∆t + |
k=−M |
|
N |
|
|
Y ( f )∑dk e− j 2 |
πfk∆t . |
(2.19) |
k=1
Как следует из формулы (2.19), частотная характеристика рекурсивного фильтра имеет вид
|
|
|
|
M |
|
|
|
H ( f ) = |
Y ( f ) |
= |
|
∑ hk e− j 2 |
πfk∆t |
|
|
|
k =−M |
|
. |
(2.20) |
|||
|
|
|
|||||
X ( f ) |
|
N |
|
||||
|
|
1−∑dk e− j2 |
πfk∆t |
|
|||
k =1
Соотношение (2.20) можно также записать в виде
|
|
|
|
M |
|
|
H (ω) = |
Y (ω) |
= |
|
∑ hk e− jωk∆t |
|
|
|
k=−M |
. |
(2.21) |
|||
X (ω) |
|
N |
||||
|
|
1−∑dk e− jωk∆t |
|
|
||
k =1
46
Соотношение между статистическими характеристиками сигналов на входе и выходе цифрового фильтра
Спектральная плотность Sy(ω) случайного сигнала y(t) на выходе линейного фильтра будет следующей:
Sy (ω) =| H (ω) |2 Sx (ω), |
(2.22) |
|||
где |
|
|
|
|
Sx (ω) = |
1 ∞ |
Kx (τ)e− jωτdτ; |
|
|
|
|
|
||
2π ∫ |
|
|||
|
|
|
||
|
|
−∞ |
|
|
Sy (ω) = |
1 ∞ |
Ky (τ)e− jωτdτ. |
|
|
|
|
|
||
2π ∫ |
|
|||
|
|
−∞ |
|
|
Здесь Sx(ω) – спектральная плотность случайного сигнала x(t) на входе фильтра; Kx(τ), Ky(τ) – корреляционные функции случайных сигналов x(t) и y(t).
Дисперсия случайного сигнала y(t)
∞ |
|
Dy = σ2y = ∫ Sy (ω)dω. |
(2.23) |
−∞
Оценка качества работы фильтра
Предположим, что на вход фильтра поступает полезный случайный сигнал g(t), на который накладывается помеха n(t). Обозначим через x(t) сигнал на входе фильтра,
x(t) = g(t) +n(t). |
(2.24) |
Предполагаем, что случайные сигналы g(t) и n(t) не коррелированны. На выходе фильтра имеем выходной сигнал y(t). Обозначим через ε(t) ошибку фильтрации, т.е.
ε(t) = y(t) − g(t). |
(2.25) |
47
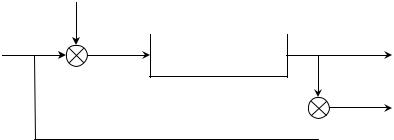
На рис. 2.11 показана схема, поясняющая процесс формирования ошибки ε(t).
n(t)
g(t) |
+ |
x(t) |
|
y(t) |
|
Фильтр
+
+ ε(t)
 –
–
Рис. 2.11. Формирование ошибки ε(t)
Спектральная плотность Sε(ω) ошибки ε(t) определяется соотношением
Sε(ω) =| H1(ω) |2 Sg (ω)+| H (ω) |2 Sn (ω), |
(2.26) |
где H1(ω) = H (ω) −1; Sg (ω), Sn (ω) – спектральные плотности
сигналов g(t) и n(t); H(ω) – частотная характеристика фильтра. Дисперсия ошибки фильтрации
∞
σε2 = Dε = ∫ Sε(ω)dω
−∞
или
σ2 |
= D = D |
+ D |
, |
(2.27) |
ε |
ε εg |
εn |
|
|
где |
|
|
|
|
|
∞ |
|
|
|
Dεg = ∫ | H1(ω) |2 Sg (ω)dω; |
(2.28) |
|||
−∞ |
|
|
|
|
48
∞ |
|
Dεn = ∫ | H (ω) |2 Sn (ω)dω. |
(2.29) |
−∞
Рассмотрим в качестве примера случай, когда частотная характеристика фильтра имеет вид
H (ω) = |
k |
, |
|
||
T ( jω) +1 |
а корреляционные функции полезного сигнала n(t) определяются соотношениями
Kg (τ) = σ2g e−α|τ|;
Kn (τ) = σ2n e−αn|τ|,
(2.30)
g(t) и помехи
(2.31)
(2.32)
где k, T – параметры фильтра; αn ,σ2n – коэффициент нерегулярности и дисперсии помехи n(t); α,σ2g – коэффициент нере-
гулярности и дисперсии сигнала g(t). Соотношениям (2.31), (2.32) соответствуют спектральные плотности
Sg (ω) = |
|
σ2g α |
|
|
|
1 |
|
, |
(2.33) |
||
|
π |
|
α2 |
+ω2 |
|||||||
|
|
|
|
|
|
|
|||||
Sn (ω) = |
σ2α |
n |
|
|
1 |
|
|
|
|
||
|
n |
|
|
|
. |
(2.34) |
|||||
|
π |
|
2 |
+ω |
2 |
||||||
|
|
|
|
|
αn |
|
|
|
|
||
Подставляем (2.30) в (2.26), получим
H1(ω) = |
(k −1) −T ( jω) . |
(2.35) |
|
T ( jω) +1 |
|
Определим | H (ω) |2 и | H1(ω) |2 в следующем виде:
| H (ω)2 |= H (ω) H (−ω), |
(2.36) |
| H1(ω) |2 = H1(ω) H1(−ω). |
(2.37) |
49
Подставляя (2.30), (2.33)–(2.37) в формулы
получим: |
|
|
|
|
|
|
|
D |
= Tα+(k −1) σ2 |
, |
|||||
εg |
|
|
Tα+1 |
g |
|
||
|
|
|
|
|
|||
D |
= |
|
k2 |
σ2. |
|
||
|
|
|
|
||||
|
εn |
|
|
Tα+1 |
n |
|
|
|
|
|
|
|
|
||
(2.28), (2.29),
(2.38)
(2.39)
Примем k = 1. Тогда из соотношения (2.27), (2.38), (2.39) имеем
|
σ2 |
Tα |
|
σ2 |
1 |
|
|
ρ = |
ε = |
|
|
+ |
n |
|
. |
|
|
Tαn +1 |
|||||
|
σ2g |
Tα+1 |
|
σ2g |
|
||
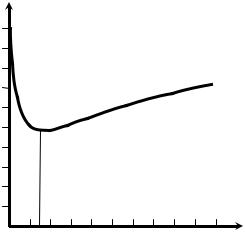
На рис. 2.12 построена зависимость ρ от Т при α = 0,02 с–1; σg = σn = 20; αn = 0,2 c−1. При проектировании фильтра выби-
рается оптимальное значение параметра Т, при котором ρ = min. Из рис. 2.12 следует, что в данном случае Топт = 15 с.
σε2 / σ2g
1,0
σg = σn = 20; αn = 0,2 c−1 α = 0,02 c−1
0,8
0,6
0,4
0,2
0 |
20 |
40 |
60 |
80 |
100 T, c |
Рис. 2.12. Зависимость ρ от Т при α = 0,02 с–1; σg = σn = 20;
αn = 0,2 c−1
50
