Лучистый поток тепла, уходящий с поверхности твердого каркаса пористой горелки, аналогично [5] в первом приближении можно рассчитать по формуле
qrad = (1− m)ε0σ(Tw4 − Th4 ) ,
где TW – температура внешней поверхности устройства, сле-
дующая из аналитического решения задачи.
Скорость сжигания газа UT также определяется на основе полученного решения при условии, что во фронте реакции, положение которого x = xf заранее неизвестно, выполняется условие непрерывности:
|
|
dTg |
|
|
dTg |
|
|
λg |
|
|
− |
λg |
|
|
= Q0UT . |
|
|
|
|
dx x= x f +0 |
|
|
dx x=x f −0 |
|
Полная задача при явном учете химического тепловыделения решается численно.
Список литературы
1.Энергетические и спектральные характеристики процесса фильтрационного горения газа в пористой металлокерамике / А.И. Кирдяшкин, Ю.М. Максимов, В.М. Орловский, Э.А. Соснин, В.Ф. Тарасенко, В.А. Панарин // Физ. гор. и взр. – 2010. – Т. 46,
№5. – С. 37–41.
2.Особенности лучистой энергоотдачи пористой горелки с металлокерамическим конвертером / В.М. Орловский, А.И. Кирдяшкин, Ю.М. Максимов, В.К. Баев, А.Н. Гущин // Оптика атмо-
сферы и океана. – 2012. – Т. 25, № 3. – С. 273–277.
3.Моделирование вхождения свободного газового пламени в пористую среду / Н.А. Какуткина, А.А. Коржавин, Е.В. Манжос, А.Д. Рычков, П.К. Сеначин // Ползуновский вестник. – 2013. –
№4/3. – С. 5–10.
4.Лаевский Ю.М., Яушева Л.В. Моделирование процессов фильтрационного горения газов в неоднородных пористых
средах // Сибирский журнал вычислительной математики. – 2009. – Т. 12, № 2. – С. 171–187.
5. Чумаков Ю.А., Князева А.Г. Стационарный режим сжигания газа в двухслойном полом пористом цилиндре // Математи-
ческое моделирование. – 2010. – Т. 22, № 7. – С. 129–147.
МНОГОТОЧЕЧНЫЕ ПРИБЛИЖЕНИЯ ВЫСШИХ ПОРЯДКОВ В СТОХАСТИЧЕСКИХ КРАЕВЫХ ЗАДАЧАХ ДЛЯ НЕОДНОРОДНЫХ
МНОГОКОМПОНЕНТНЫХ СРЕД
М.А. Ташкинов, Е.М. Спаскова, П.С. Бажуков
Пермский национальный исследовательский политехнический университет,
Пермь, Россия, m.tashkinov@pstu.ru, cem.spaskova@mail.ru, 9641979675cem@gmail.com
Работа посвящена разработке статистических подходов для описания процессов деформирования неоднородных многокомпонентных сред. В качестве характеристик полей напряжений и деформаций в представительном объеме при нагружении используются статистические моменты, аналитический вид которых получен с использованием второго приближения стохастической краевой задачи. Полученный аналитический инструмент позволяет производить расчет статистических характеристик для каждой компоненты среды в отдельности.
Ключевые слова: многокомпонентные среды, краевые задачи, случайная микроструктура, статистические характеристики.
В настоящее время все большее распространение получают материалы, комбинирующие в себе свойства трех и более компонент и благодаря этому обладающие улучшенными характеристиками и расширенным функционалом. Простейшим примером многокомпонентного материала могут служить композиты, в микроструктуре которых помимо матрицы и наполнителя содержатся поры, возникшие как результат технологических производственных процессов. Одной из особенностей многокомпонентных сред зачастую является случайность геометрических и физических па-
раметров внутренней микроструктуры. Исследования в области вычислительной и экспериментальной механики случайных параметров показали, что такие параметры, как объемная доля фаз, ориентация, форма, размер и пространственное распределение включений, играют существенную роль в поведении многокомпонентных материалов [1–3]. Таким образом, актуальной задачей является создание нелинейных моделей, способных учесть особенности случайной непериодической многокомпонентной микроструктурыподобных материалов.
Для исследования непериодических случайным образом армированных композитов широко используются статистические методы, основанные на теории случайных функций [4–8]. Согласно подобным подходам поля напряжений, деформаций и перемещений на микроструктурном уровне могут быть представлены в виде статистически однородных кусочно-постоянных функций координат, а в качестве характеристик процессов деформирования в компонентах композита могут быть введены многоточечные статистические моменты стохастических полей напряжений и деформаций, характеризующие параметры статистического разброса значений полей. Аналитические выражения для статистических характеристик полей напряжений и деформаций в компонентах композитов, а также выражения для эффективных модулей упругости находятся с помощью статистического осреднения интегродифференциальных уравнений, содержащих моментные функции, и получаемых на основе решения стохастических краевых задач.
Целью работы является развитие методов исследования полей структурных напряжений и деформаций для случая многокомпонентных неоднородных сред на основе построения многоточечных приближений решений стохастических краевых задач.
Решение краевой задачи записывается с использованием функций Грина. В качестве входных параметров математической модели выступают механические свойства компонент представительного объема, входящих в функции Грина, а также геометриче-
ские характеристики представительного объема рассматриваемой среды, которые определяются структурными моментными функциями. Граничные условия стохастической краевой задачи определяютхарактернагруженияпредставительногообъема.
Для вывода аналитических выражений для моментов полей напряжений и деформаций использовалось решение краевой задачи во втором приближении, позволяющее в более полной степени учитывать особенности геометрии неоднородной среды посредством структурных моментных функций высокого (до пятого) порядка.
Получено представление моментных функций n-го порядка полей напряжений и деформаций в общем виде. Так, выражение для момента n-го порядка полей напряжений записывается в следующем виде:
|
|
( |
|
|
|
|
) = |
n |
n! |
|
(n−i) |
1 |
|
|
|
|
|
|
|
|
|
(n) |
|
|
|
|
|
|
|
(i) |
|
(σ ) |
|
|
|
|
|
|
|
|
|
|
M |
|
|
r |
− x |
|
|
|
σ |
|
|
λ |
|
σ |
|
+ D |
|
|
− |
|
|
|
|
|
|
|
|
|
|
σC |
|
|
|
|
|
|
i!(n − i)! |
|
|
λC |
|
C |
|
|
(i) |
|
|
|
|
|
|
|
|
|
|
i=0 |
|
|
|
|
|
|
|
|
|
|
|
n−1 |
n! |
|
|
|
− |
D((iσ)C ) σ C(n−i) , |
|
i!(n − i)! |
|
i=0 |
|
где
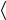 σ
σ (n−i) =
(n−i) = 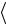 σij
σij 
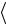 σαβ
σαβ ...
...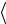 σxy
σxy  ,
,
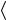 σ
σ C(n−i) =
C(n−i) = 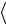 σij
σij  C
C 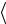 σαβ
σαβ C ...
C ... σxy
σxy  C ,
C ,
λσ(i) = |
λ′ |
(r )σ′ |
(r )σ′ |
(x)...σ′ |
(τ) , |
|
C |
|
ij |
|
αβ |
|
xy |
|
D(σ) |
= σ′ |
(r )σ′ |
(x)...σ′ |
(τ) |
, |
(i) |
|
ij |
|
αβ |
|
xy |
|
|
D(σC ) |
= σ′ |
(r )σ′ |
(x)...σ′ |
(τ) . |
(i) |
|
ij |
|
αβ |
|
xy |
|
C |
Значения структурных моментных функций могут быть вычислены на основе анализа геометрической модели предста-
вительного объема. Созданы трехмерные модели представительных объемов многокомпонентных композитов с различными геометрическими параметрами армирующих включений и характеристиками их распределения. Для представительных объемов получены значения моментных функций высших порядков, проведена их аппроксимация.
Для рассмотренных частных случаев представительных объемов проведены расчеты статистических характеристик. Для верификации полученных результатов использованы структурные конечно-элементные модели.
Методика расчета значений моментов полей деформирования в упругом и упругопластическом случае при различных условиях нагружения представительных объемов и физико-механи- ческих характеристиках компонент реализована в виде программных инструментов в среде Wolfram Mathematica с использованием возможностейвстроенныхфункций ипараллельныхвычислений.
Работа выполнена при поддержке гранта Президента Российской Федерации для государственной поддержки молодых российских ученых – кандидатов наук (МК-5172.2015) и гранта № 16-41-590259-р_урал_а Российского фонда фундаментальных исследований.
Список литературы
1.Torquato S. Random heterogenous materials, microstructure and macroscopic properties. – Springer, 2001. – 701 p.
2.Buryachenko V. Micromechanics of heterogeneous materials. – New York, Springer, 2007. – 686 p.
3.Rasool A., Böhm H.J. Effects of particle shape on the macroscopic and microscopic linear behaviors of particle reinforced
composites // International Journal of Engineering Science. – 2012. – Vol. 58. – Р. 21–34. DOI: 10.1016/j.ijengsci.2012.03.022.
4. Волков С.Д., Ставров В.П. Статистическая механика композитных материалов. – Минск: Изд-во Белорус. гос. ун-та, 1978. – 208 с.
5.Шермергор Т.Д. Теория упругости микронеоднородных сред. – М.: Наука, 1976. – 400 с.
6.Вильдеман В.Э., Соколкин Ю.В., Ташкинов А.А. Механика неупругого деформирования и разрушения композиционных материалов. – М.: Наука, 1997. – 288 с.
7.Tashkinov M. Statistical characteristics of structural stochastic stress and strain fields in polydisperse heterogeneous solid
media // Computational Materials Science. – 2014. – Vol. 94. –
P.44–50. DOI: 10.1016/j.commatsci.2014.01.050.
8.Ташкинов М.А., Вильдеман В.Э., Михайлова Н.В. Метод последовательных приближений в стохастической краевой задаче теории упругости структурно-неоднородных сред // Механика
композиционных материалов и конструкций. – 2010. – Т. 16. –
№3. – С. 369–384.
МОДЕЛИРОВАНИЕ РОТАЦИЙ КРИСТАЛЛИЧЕСКИХ РЕШЁТОК ПРИ ОПИСАНИИ ФРАГМЕНТАЦИИ И ДРОБЛЕНИЯ ЗЕРЕН В ПРОЦЕССАХ ИНТЕНСИВНЫХ НЕУПРУГИХ ДЕФОРМАЦИЙ
М.А. Тельканов, П.С. Волегов
Пермский национальный исследовательский политехнический университет,
Пермь, Россия, michaelperm@gmail.com
В работе представлена модификация модели ротаций кристаллических решёток зёрен и их фрагментов с целью описания процессов фрагментации и дробления зёрен. Для определения степени разориентации решёток зёрен предлагается мера, основанная на взаимном положении проекций стереографических направлений кристаллических решеток на стандартном стереографическом треугольнике (ССТ). Проведена качественная оценка удельной энергии, затрачиваемой на ротации.
Ключевые слова: физические теории пластичности, многоуровневые модели, поликристалл, ротации, фрагментация зерен.
С появлением новых задач, связанных с технологиями изготовления металлов и конструкций из них, становится необходимым развитие новых методов математического моделирования
процессов получения и обработки материалов. Так как внедрение
впроизводство новых технологий обработки металлов связано со значительными расходами на исследования, в последнее время
вданной области часто применяется аппарат математического моделирования, а именно использование многоуровневых математических моделей деформирования представительного объёма поликристаллического агрегата [1].
Обработка металлов на производстве, как правило, связана с интенсивными пластическими деформациями, которые сопровождаются такими явлениями, как повороты (ротации) кристаллических решёток, фрагментация и дробление зёрен металла. Фрагментацией называется процесс, при котором внутри одного кристаллита появляются слабо разориентированные области (фрагменты), разделённые малоугловыми границами [2]. Под дроблением понимается процесс формирования новых зёрен, разделённых большеугловыми границами. Каждый из перечисленных процессов вносит существенный вклад в физикомеханические свойства материала, поэтому задача полного описания эволюции фрагментно-зёренной структуры материала представляется крайне актуальной. Так, ротации кристаллических решёток зёрен и их фрагментов приводят к образованию кристаллографической текстуры материала. Текстура материала порождает существенную анизотропию его свойств, которую необходимо учитывать при эксплуатации конструкций из данного материала. Фрагментация приводит к изменению дефектной структуры материала, дробление же оказывает влияние на предел его текучести [3]. Таким образом, создание математических моделей неупругого деформирования поликристаллов, учитывающихописанныепроцессы, является актуальнойзадачей.
Вработе для описания процессов деформации поликристаллов применена двухуровневая модель неупругого деформирования поликристаллов [1] с выделением промежуточного масштабного квазиуровня (зерна) – совокупности слаборазориентированных фрагментов, отделенных друг от друга большеуг-
ловыми границами [4]. В таком случае элементом нижнего масштабного уровня становится отдельный фрагмент с однородной ориентацией кристаллической решетки. Для описания ротаций использована модель, связанная с несовместностью пластических сдвигов [5]. Эта модель имеет чёткие физические причины разворотов кристаллических решеток и может быть применена для любого связного подмножества элементов. В процессе деформирования вращаться могут как отдельные зёрна, так и фрагменты зёрен, поэтому для удобства назовём структурную единицу, вращающуюся в данный момент как единое целое, элементом ротации (ЭР).
Вмодель внесены два ключевых изменения. Первое связано
сналожением вращений на разных масштабных уровнях, предлагается схема наложения вращений «сверху-вниз». Это означает, что поворот решетки фрагментов зёрен будет состоять не только из собственного вращения, но еще из поворота зерна, в состав которого входит данный фрагмент, и из поворота представительного объема как жесткого целого. Собственное вращение ЭР описывается следующим образом:
где ωсоб – тензор спина решётки, E – тензор Леви–Чивита, e –
мгновенная ось вращения решётки ЭР, определяемые по модели ротаций [5].
Спин решетки фрагмента представляется суммой трёх слагаемых, первое из которых совпадает со спином решетки из модели стеснённого поворота по Тейлору и описывает поворот решётки какжёсткогоцелого:
K |
|
|
|
|
ωфр = w − 1 |
γ((ik)) (n(k )b(k ) |
- b(k )n(k ) ) + ωсоб + ωзерна , |
(2) |
k =1 |
2 |
|
|
|
где w – тензор вихря, n(k ) и b(k ) – вектора нормали и Бюргерса для k-й СС.
c(i)
Вторая существенная модификация модели связана с введением так называемого ротационного упрочнения. По аналогии с упрочнением в классическом его понимании, т.е. увеличении критических касательных напряжений по системам скольжения, предлагается закон, описывающий рост критической величины объемного момента M с увеличением накопленного угла раз-
ворота. В предположении о том, что критический вращательный момент зависит от накопленного поворота и размеров самого кристаллита, было записано следующее соотношение:
Mc(i) = |
K1 |
exp(−K2Φ(i) ), |
(3) |
|
V(i) |
|
|
где K1 и K2 – параметры материала, Φ(i) (t ) – накопленный
поворот решетки, Φ(i) (t ) = t |
ωфр : ωфр dτ. С физической точки |
0 |
|
зрения это означает, что с увеличением пластических деформаций структура приграничных областей существенно усложняется, что затрудняет движение дислокаций сквозь неё, и рано или поздно критическая величина объёмного момента достигнет такого значения, что дальнейший поворот решетки станет невозможен.
Для определения больше- и малоугловых границ предлагается использование меры, основанной на взаимном положении проекций стереографических направлений на стандартном треугольнике. При этом большеугловыми считаются границы, значение меры для которых больше, чем значение для «эталонной» границы наклона в 15°.
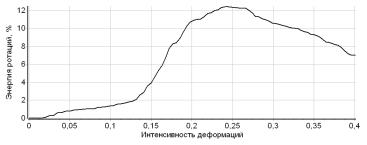
В рамках работы было проведено исследование удельной мощности, затрачиваемой системой на ротации кристаллических решёток. На рисунке представлено отношение энергии, приходящейся на ротации, к полной энергии деформирования для эксперимента по одноосному растяжению поликристалла меди.
Рис. Зависимость доли энергии ротаций от интенсивности деформации
Из рисунка видно, что относительная доля энергии, приходящейся на ротации кристаллических решеток ЭР, может достигать весьма значительных значений (до 12 %); таким образом, учёт ротаций кристаллических решёток является необходимым для адекватного описания процессов деформирования.
Работа выполнена при финансовой поддержке гранта Пре-
зидента РФ № МК-4917.2015.1, РФФИ (грант № 14-01-96008
р_урал_а), гранта Правительства Российской Федерации (Постановление № 220 от 9 апреля 2010 г., договор № 14.В25.310006 от
24 июня 2013 г.).
Список литературы
1.Трусов П.В., Швейкин А.И. Многоуровневые физические модели моно- и поликристаллов. Статистические модели //
Физ. мезомеханика. – 2011. – № 4. – С. 17–28.
2.Орлов А.Н., Перезвенцев В.Н., Рыбин В.В. Границы зерен в металлах. – М.: Металлургия, 1980. – 154 с.
3.Козлов Э.В., Жданов А.Н., Конева Н.А. Механизмы деформации и механические свойства наноматериалов // Физ. мезо-
механика. – 2007. – № 3. – С. 95–103.
4.Тельканов М.А., Волегов П.С. Описание ротаций кристаллических решеток и фрагментации зерен при интенсивных
380



 σ
σ
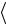 σ
σ
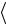 σ
σ ...
...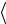 σ
σ ,
,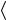 σ
σ
 σ
σ
 σ
σ
 σ
σ