Дискретно-полевые модели электрических машин. Часть I II

12. СИНХРОННЫЙ НЕЯВНОПОЛЮСНЫЙ ГЕНЕРАТОР

Синхронный генератор с неявно выраженными полюсами (СНЯГ) предназначен для работы с частотой вращения 1500 и 3000 об/мин. Онимеет ротор, выполненный из цельнометаллической поковки, в пазах которой располагаются проводники обмотки возбуждения. Статор генератора имеет магнитопровод, выполненный из электротехнической стали, в пазах статора располагаются проводники трёхфазной обмотки. Генераторы этой конструкции не имеют специальной демпферной обмотки. Её роль выполняет массивный магнитопровод ротора и клинья из проводящего материала, предназначенные для крепления проводников обмотки возбуждения. Характерной особенностью этих генераторов является равномерность воздушного зазора на всём протяжении полюсного деления, что обусловливает симметриюмагнитной системы.

При построении математической модели синхронного генератора будем считать, что система уравнений генератора является линейной. В этом случае оказывается справедливым принцип суперпозиции, и магнитное поле машины может рассматриваться в виде комбинации нескольких составляющих. Одна из них определяется током обмотки возбуждения. Вторая составляющая представляет собой поле якоря, а третья – поле, создаваемое демпферной обмоткой. Для различных режимов работы синхронного генератора возможны различные комбинации этих составляющих. В целом же магнитное поле генератора едино, а представление его в виде комбинации отдельных составляющих введено для упрощения решения рассматриваемых задач.

12.1. РЕЖИМ ХОЛОСТОГО ХОДА СИНХРОННОГО НЕЯВНОПОЛЮСНОГО ГЕНЕРАТОРА

Положим, что к обмотке возбуждения приложено постоянное напряжение, под действием которого по обмотке протекает ток возбуждения. Обмотка статора разомкнута, и ток нагрузки генератора отсутствует. В стационарных режимах отсутствуют вихревые токи

401

массивного ротора и крепёжных клиньев. Магнитное поле генератора создаётся, таким образом, током обмотки возбуждения, которая вращается в пространстве с синхронной скоростью. Так же как и в предыдущих случаях, решение задачи будем производить в системе координат, связанной с неподвижным статором. В этом случае демпферная обмотка и обмотка возбуждения вращаются в пространстве относительно статора с синхронной скоростью. ЭДС проводников обмоток ротора будут содержать как трансформаторные составляющие, так и ЭДС вращения. ЭДС проводников обмотки статора будут содержать трансформаторную составляющую, ЭДС вращения будет равна нулю.

При исследовании магнитного поля генератора с использованием одномерной модели приняты те же упрощающие допущения, что и при исследовании аналогичного режима асинхронных машин. В этом случае магнитное поле генератора описывается одномерным уравнением, с краевыми условиями периодического типа,

где J в , J д – плотности тока обмоток возбуждения и демпферной. Принимая во внимание, что решение уравнения находится для

воздушного зазора с магнитной проницаемостью µ 0 , уравнение (12.1) может быть упрощено и приведено к виду

В стационарном режиме холостого хода ток демпферной обмотки отсутствует, и магнитное поле генератора определяется лишь токами обмотки возбуждения, проводники которой распределены в пространстве. Для получения ЭДС с минимальным количеством высших гармоник отношение обмотанной и необмотанной части полюсного деления ротора должно находиться в пределах 0,65–0,75. Подбирая это соотношение в указанных пределах, можно получить распределение МДС, близкое к синусоидальному.

402

Векторный потенциал магнитного поля при известном пространственном распределении плотности тока возбуждения определяется решением уравнения (12.2) при равенстве нулю тока демпферной обмотки.

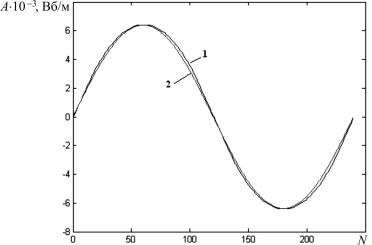
На рис. 12.1 и 12.2 показан характер распределения МДС обмотки возбуждения в пространстве и получаемое при этом распределение векторного потенциала магнитного поля, полученного в результате решения дифференциального уравнения.

Рис. 12.1. Распределение плотности тока обмотки возбуждения вдоль расточки статора

На рис. 12.2 видно, что векторный потенциал магнитного поля с высокой точностью может быть описан зависимостью

где Aм – комплексная амплитуда векторного потенциала; φ0 – вектор начальных значений угловых координат проводников обмотки возбуждения; j = −1 – мнимая единица.

403

Таким образом, магнитное поле в воздушном зазоре генератора распределено по синусоидальному закону с указанной амплитудой.

Обмотка возбуждения генератора обтекается постоянным током и вращается в пространстве с синхронной частотой вращения ω0 .

При этом проводники обмотки возбуждения занимают различное пространственное положение относительно неподвижного статора, причём пространственная координата проводников возрастает пропорционально времени. В этом случае векторный потенциал является функцией времени и может быть записан в виде

Напряжённость электрического поля в движущемся проводнике, создаваемая магнитным полем, определяется выражением (8.29). Для неподвижного проводника обмотки якоря напряжённость электрического поля записывается в виде

Учитывая, что для рассматриваемой одномерной модели напряжённость электрического поля, как и векторный потенциал, имеет по единственной аксиальной составляющей, для стационарного режима это уравнение можно представить как

ЭДС витка обмотки якоря определяется через циркуляцию напряжённости электрического поля:

405

В условиях одномерной задачи при бесконечной длине статора ЭДС лобовых частей представляется в виде ЭДС рассеяния лобовых частей, и поэтому

сти электрического поля в точках, координаты которых соответствуют координатам сторон витка.

Если обмотка выполнена с полным шагом, то координаты сторон витка отличаются на угол, соответствующий полюсному делению. В этом случае ЭДС витка равна удвоенному значению ЭДС стороны витка. При укороченной обмотке координаты сторон соответствуют шагу обмотки. Укорочение обмотки, таким образом, учитывается автоматически.

ЭДС катушки при условии равенства всех магнитных потоков, пронизывающих витки катушки

где q – число катушек в катушечной группе.

Поскольку катушки катушечной группы распределены в пространстве, то ЭДС отдельных катушек сдвинуты во времени по фазе и распределение обмотки также учитывается автоматически.

Фазная ЭДС представляет сумму ЭДС катушечных групп, каждая из которых соответствует паре полюсов. Следовательно, при последовательном соединении катушечных групп

Фазные обмотки статора смещены в пространстве на треть периода. Соответственно координаты проводников различных фаз так-

406

же отличаются на эту величину. Поэтому и ЭДС фазных обмоток смещены по фазе на 120 электрических градусов.

Реально пространственное распределение магнитного поля в воздушном зазоре генератора отлично от синусоидального. Магнитное поле содержит спектр высших пространственных гармоник, которые наводят в обмотках статора высшие временные гармоники ЭДС. Подавление этих гармоник осуществляется за счёт укорочения и распределения обмоток, так же как и в асинхронных машинах.

Представленные выше формулы позволяют рассчитать характеристику холостого хода – зависимость фазной ЭДС генератора от тока возбуждения. Учёт насыщения магнитной системы генератора производится корректированием величины коэффициента qm в уравнении (12.2) при изменении магнитной проницаемости ферромагнитных участков магнитной цепи в процессе их насыщения.

В соответствии с изложенным разработана программа расчёта характеристики холостого хода – зависимости фазной ЭДС генератора от тока возбуждения. Программа сводится к решению дифференциального уравнения (12.2) при коэффициенте qm, зависящем от насыщения ярма статора и ротора генератора. По найденным значениям векторного потенциала рассчитываются ЭДС витка, катушки, катушечной группы фазной обмотки для разных значений тока возбуждения. Расчёт магнитного поля СНЯГ в режиме холостого хода приведён в следующем примере.

Пример 12.1. Расчёт магнитного поля и характеристики холостого хода синхронного неявнополюсного генератора. Рассчи-

тать характер распределения магнитного поля вдоль расточки статора образца синхронного неявнополюсного генератора, имеющего следующие параметры:

–частота тока 50 Гц;

–число полюсов 2;

–радиус расточки статора 45,5 10–3 м;

–воздушный зазор 0,5 10–3 м;

–высота ярма статора 15,2 10–3 м;

–высота ярма якоря 15,4 10–3 м;

407

–длина статора 0,1 м;

–число пазов якоря 16;

–число пазов статора 30;

–число проводников в пазу якоря 80;

–число проводников в пазу статора 200;

–обмотка статора – однослойная.

Программа расчёта магнитного поля и характеристики холостого хода СНЯГ:

n=240; ff(1:n)=0.; r0=45.5e-3; mu0=4.*pi*1.e-7;om=314.15926; ew(1:n)=0.; wb=20.; la=0.1; hf=2.*pi/n; ha=15.4e-3;hs=15.2e-3; me=0.+1.i; wa=8.; del=0.5e-3; nn=1;tokb=0.0; dtokb=0.05; tokbk=1.0; alf0=2.*pi/n; jh=15; db=0.1; bt(1)=0.0;

for j=1:29 bt(j+1)=bt(j)+db;

end

for j=1:6 mu(j)=2580; end

mu(7)=2540.; mu(8)=2500.; mu(9)=2468.; mu(10)=2463.; mu(11)=2457.; mu(12)=2367;

mu(13)=2253.; mu(14)=2129.; mu(15)=1900.; mu(16)=1684.3; mu(17)=1498.; mu(18)=1177;

mu(19)=942; mu(20)=731; mu(21)=505; mu(22)=325; mu(23)=196; mu(24)=167.;

mu(25)=140; mu(26)=124;mu(27)=99.;mu(28)=75.;mu(29)=57.; mu(30)=27.; X=[bt(1:30)]; Y=[mu(1:30)]; prs(1:n)=2540.; pra(1:n)=2540.; rs1=(hs+del)/(2.*r0); rs2=1+rs1; ra1=(ha+del)/(2.*r0); ra2=1.-ra1;

while tokb<tokbk for j=1:n

rs=rs2/(prs(j)*hs*del); ra=ra2/(pra(j)*ha*del); qq(j)=rs+ra; end

a(1:n)=0.; b(1:n)=0.; c(1:n)=0.; tf=tokb*wb/(del*r0*hf); for j=jh+1:jh+6

ff(j)=tf; ff(j+12)=tf; ff(j+24)=tf; ff(j+36)=tf; ff(j+48)=tf; ff(j+60)=tf;ff(j+72)=tf;ff(j+84)=tf;

end

for j=1:120 ff(j+120)=-ff(j);

end

408

for j=1:n ft(j)=mu0*ff(j)*r0^2*hf^2;

end y(1:n)=0.; for j=1:n

a(j)=1.0; b(j)=1.0; c(j)=a(j)+b(j)+r0^2*hf^2*qq(j); end

alf(2)=b(1)/c(1); bet(2)=ft(1)/c(1); gam(2)=a(1)/c(1); for j=2:n

r1=c(j)-alf(j)*a(j); alf(j+1)=b(j)/r1; r2=ft(j)+a(j)*bet(j); bet(j+1)=r2/r1; gam(j+1)=gam(j)*a(j)/r1;

end

p(n-1)=bet(n); q(n-1)=alf(n)+gam(n); for j=n-2:-1:1

p(j)=alf(j+1)*p(j+1)+bet(j+1); q(j)=alf(j+1)*q(j+1)+gam(j+1); end

r3=bet(n+1)+alf(n+1)*p(1); r4=1.-gam(n+1)-alf(n+1)*q(1); y(n)=r3/r4; for j=1:n-1

y(j)=p(j)+y(n)*q(j); end

[ym,I]=max(y);

I=60; for j=1:n

j1=j-I;

if j1<0 j1=j1+n; end yy(j)=ym*exp(i*alf0*j1);

end

br(1)=(yy(2)-yy(n))/(2.*r0*hf); br(n)=(yy(1)-yy(n-1))/(2.*r0*hf); for j=2:n-1

br(j)=(yy(j+1)-yy(j-1))/(2.*r0*hf); end

for j=1:n

bs(j)=yy(j)/hs; ba(j)=-yy(j)/ha; end

BB=[abs(real(bs(1:n)))];mub=interp1(X,Y,BB);

prs(1:n)=mub(1:n);

BA=[abs(real(ba(1:n)))];mua=interp1(X,Y,BA);

pra(1:n)=mua(1:n);

pota1=0.; pota2=0.; potb1=0.; potb2=0.; potc1=0.; potc2=0.; for j=1:5

pota1=pota1+yy(j)+yy(j+8)+yy(j+16)+yy(j+24)+yy(j+32);

409

pota2=pota2+yy(j+120)+yy(j+128)+yy(j+136)+yy(j+144)+yy(j+152); pota=la*wa*(pota1-pota2); potb1=potb1+yy(j+80)+yy(j+88)+yy(j+96)+yy(j+104)+yy(j+112); potb2=potb2+yy(j+200)+yy(j+208)+yy(j+216)+yy(j+224)+yy(j+232); potb=la*wa*(potb1-potb2); potc1=potc1+yy(j+160)+yy(j+168)+yy(j+176)+yy(j+184)+yy(j+192); potc2=potc2+yy(j+40)+yy(j+48)+yy(j+56)+yy(j+64)+yy(j+72); potc=la*wa*(potc1-potc2);

end

edsa=-me*om*pota; edsb=-me*om*potb; edsc=-me*om*potc; disp(nn);disp(edsa); disp(edsb); disp(edsc);

n1(nn)=tokb; n2(nn)=abs(edsa);nn=nn+1;tokb=tokb+dtokb; end

plot(y);

Результаты моделирования режима холостого хода СНЯГ представлены на рис. 12.3 и 12.4.

Рис. 12.3. Распределение векторного потенциала вдоль расточки статора СНЯГ

410